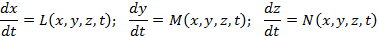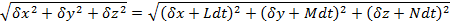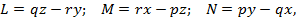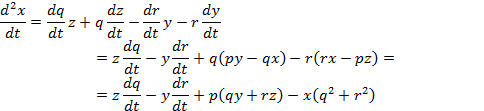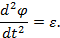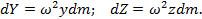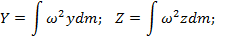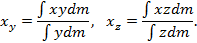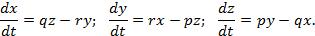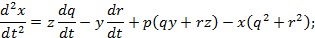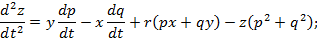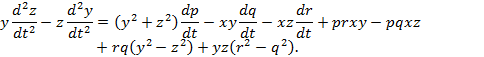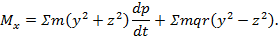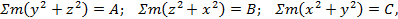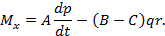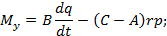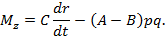Видео:Сферическое движениеСкачать

Динамические уравнения Эйлера
- Динамическое уравнение Эйлера для вращения объекта вокруг неподвижной точки под действием силы можно вывести из теоремы об изменении момента движения. Согласно этой теореме, dKoldt = L ^>, (10) Где Ko — момент движения тела относительно неподвижной точки от вращения тела относительно инерциальной системы отсчета. D> | = X — векторная сумма моментов Т внешней силы, действующей на тело (рис. 135). Среди внешних сил есть сила реакции в фиксированной точке.
Когда снаряд находится в движении, его центр тяжести движется так, как если бы в нем была сосредоточена вся масса тела и к нему были приложены все действующие на снаряд внешние силы. Людмила Фирмаль
Когда (10) представляется проекцией на инерциальную (фиксированную) координатную ось, моменты, которые меняются со временем, в зависимости от конкретного случая основных (3) и (4) главных осей, через Kx, Ku, K В том числе обычное уравнение инерции. Это расчет, который уже должен знать движение тела, и сам должен определяться силой, данной. Чтобы избежать этого, Эйлер предложил проецировать вектор (10) на движущуюся ось координат, прикрепленную к вращающемуся телу.
- Для таких осей момент инерции не зависит от времени. Подготовьте векторное уравнение (10) для проекции на оси подвижных координат, закрепленных на движущемся объекте. По этой причине абсолютная производная по времени от момента движения должна быть выражена как относительная производная по формуле Бора. + К. Болезнь.
Это связано с тем, что система перемещения осей координат имеет ту же угловую скорость, что и само тело, с которым эти оси связаны. Представлено векторное поколение для удобства проецирования Удалить вектор в виде определителя, затем развернуть до элементов первой строки, т.е. | J K I шхко = тсс шу юг = / (шу ^ 1-шхх) + | к * к, кг я + j (azKx-axKz) + H (axKy-ayKx), (12) где i, j и H — единичные векторы, ориентированные вдоль осей координат движущейся системы координат.
В разделе упражнений будет показано, что систему векторов можно всегда привести к таким двум векторам, из которых Ъдин лежит на произвольной прямой, не параллельной главному вектору. Людмила Фирмаль
Используйте уравнение (I) для выражения теоремы об изменении момента движения (10) в следующем виде: Рисунок 135 В проекции на ось подвижной координаты, прикрепленной к вращающемуся телу, с учетом (10 ‘) — (12), ^ + — (15) sog = f cos6 4-f, Это представляет проекцию угловой скорости вращения объекта на движущиеся координатные оси, прикрепленные к объекту через углы Эйлера f, 6, f и их производные по времени.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Кинематика твердого тела. Формула Эйлера. Формула Ривальса. Угловые скорости.Скачать

Please wait.
Видео:Лекция 06 Динамика твердого телаСкачать

We are checking your browser. gufo.me
Видео:Динамические уравнения ЭйлераСкачать

Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Теормех. 2021-дек-22. Уравнения движения твердого телаСкачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Cloudflare Ray ID: 6e28e0afda707b2f • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:§5.1. Уравнения сферического движения твердого телаСкачать

Тема 27. Движение твердого тела. Работы Эйлера берлинского периода
После отъезда из России Эйлер был приглашен прусским королем Фридрихом II в Берлинскую Академию наук.
Возобновление работы пришлось вести уже в другой обстановке.
Данное Ньютоном решение задачи об исследовании планетного движения предполагало, что планеты являются материальными точками. Теперь планеты, в частности Землю и Луну, надо было рассматривать как твердые тела. Для этого в первую очередь пришлось установить более точно форму Земли, которую уже нельзя было рассматривать как геометрический шар. Эта задача тоже была поставлена Ньютоном, который считал, что Земля представляет сплюснутый к экватору эллипсоид вращения. Во Франции появилась другая теория, которую защищали парижские астрономы Кассини ; для решения этого вопроса пришлось отправить две геодезические экспедиции: одну на север — в Лапландию, другую на юг — в Перу. Результаты этой экспедиции показали, что прав был Ньютон, а не Кассини , предполагавшие на основе предшествующих не слишком точных геодезических измерений, что Земля представляет эллипсоид вращения, вытянутый к полюсам.
Если Земля является точным шаром, то задача о силе ее притяжения других тел была уже решена Ньютоном: Земля притягивает другие планеты, как если бы вся ее масса была сосредоточена в ее центре. Но если Земля представляет эллипсоид, то силу ее притяжения необходимо определить заново. Этой задачей занялись английские ученые Маклорен (1698—1746) и Айвари ( Jvory ), определившие силы притяжения эллипсоидов.
Вторая задача касалась определения движения планет, рассматриваемых как твердое тело. Уже давно было известно, что Земля кроме вращения вокруг собственной оси и обращения вокруг Солнца имеет еще два движения, а именно: известное еще Гиппарху прецессионное движение, которое было достаточно хорошо вычислено математически, но совершенно не объяснено динамически, и недавно открытая Брадлеем нутация земной оси. Этими вопросами занялись Алексис Клеро (1713—1765) и Д ‘Аламбер .
Клеро очень рано проявил свой математический талант и в восемнадцать лет был принят в члены Парижской академии. Он принимал участие во французской экспедиции по измерению градуса меридиана в Лапландии (1736—1737), и опубликованная в 1743 г. его «Теория фигуры Земли» положила начало высшей геодезии. Он принимал участие в предвычислении появления кометы Галлея и пытался построить математическую теорию движения Луны.
Д’Аламбер в 1749 г. выпустил «Трактат о предварении равноденствий и нутации земной оси», а в 1761 г. — мемуар «О движении тел произвольной формы под действием произвольных сил». Параллельно с ним и совершенно независимо от него вел работу Эйлер. В 1750 г. он написал статью «Открытие нового принципа механики» («Записки Берлинской Академии наук», т. 14, стр. 185—217). Ему пришлось начинать с кинематики, и первое, что он сделал, это вместо своих естественных уравнений движения материальной точки принял введенные Маклореном уравнения движения, разложенные по прямоугольным координатным осям. Это позволило ему дать формулу для скорости точки во вращательном движении твердого тела. Поставленная им задача имела несколько необычную чисто математическую форму. Требовалось найти такие функции L, М, N, которые могли бы удовлетворять уравнениям
dx dt = L x , y , z , t ; dy dt = M x , y , z , t ; dz dt = N x , y , z , t
при условии сохранения неизменности расстояний между точками абсолютно твердого тела:
δ x 2 + δ y 2 + δ z 2 = δx + Ldt 2 + δy + Mdt 2 + δz + Ndt 2
для любых возможных перемещений тела.
Оказалось, что искомые функции L, M, N должны иметь вид:
L = qz — ry ; M = rx — pz ; N = py — qx ,
где p, q, r — любые функции времени. Это хорошо известные уравнения Эйлера, в которых р , q, r — суть проекции на координатные оси угловой скорости со. Понятие угловой скорости тела в это время было Эйлеру неизвестно; он определяет угловую скорость вращающегося вокруг неподвижной оси твердого тела как скорость точки, расстояние от которой до оси вращения принято за единицу ( unitate exprimitur ). Термина «угловое ускорение» не было, но проекции линейных ускорений можно было получить простым дифференцированием скоростей
d 2 x dt = dq dt z + q dz dt — dr dt y — r dy dt = z dq dt — y dr dt + q py — qx — r rx — pz == z dq dt — y dr dt + p qy + rz — x q 2 + r 2
и аналогично для остальных.
Таким образом началась работа, которая потребовала 25 лет для того, чтобы получить знаменитые динамические уравнения Эйлера для движения твердого тела.
В сочинении «Теория движения твердых тел» Эйлер последовательно рассматривает поступательное ( progressivus ) и вращательное ( gyratorius ) движения, а затем и общий случай движения твердого тела.
Поступательным он называет движение, в котором отдельные точки тела в любой момент времени движутся с одинаковыми скоростями по взаимно параллельным направлениям. Основным признаком вращательного движения он считает наличие оси вращения — жестко соединенной с телом прямой, вокруг которой происходит движение тела. Если эта ось неподвижна, то скорости точек тела пропорциональны их расстояниям до этой оси. На этом этапе появляется уже цитированное выше определение угловой скорости.
В качестве углового ускорения Эйлер пользовался величиной а, которую он определял из выражения dω = αd t 2 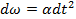
d 2 φ dt 2 = ε .
При рассмотрении этих движений Эйлер ставил три задачи:
1. Привести к простейшему виду систему сил, действующих на тело.
2. Определить получающееся движение.
3. Найти величину сил, действующих на связи.
Если вращение происходит с постоянной угловой скоростью со , то система действующих на тело сил равна нулю. Давление на ось складывается из элементарных центробежных сил. Если ось вращения О х и угловая скорость ω, то центробежная сила, действующая на точку с координатами х, у, z и элементарной массой dm , распадается на две составляющие
dY = ω 2 ydm ; dZ = ω 2 zdm .
Складывая отдельно элементарные силы по осям y и z, Эйлер получил две взаимно перпендикулярные силы
Y = ω 2 ydm ; Z = ω 2 zdm ;
приложенные к оси вращения в двух точках с абсциссами
x y = xydm ydm , x z = xzdm zdm .
Таким образом, система центробежных сил инерции приводится к двум взаимно перпендикулярным силам X и Z, приложенным к оси вращения в двух различных точках. Современная система «моторов» Мизеса уже была знакома Эйлеру.
Если тело вращалось с ускорением е, то последнее определялось как частное от деления момента движущей силы на величину r 2 dm 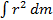
Понятие о моменте инерции уже было введено Эйлером при составлении первого тома «Морской науки», где он дал определение момента инерции, вычислил его для некоторых наиболее простых тел. При вычислении их он доказывает теорему о параллельных осях, известную теперь под именем теоремы Штейнера или Гюйгенса.
При определении центра качания Гюйгенс пользовался упомянутым соотношением, но он не обратил внимания на употреблявшуюся им при вычислениях величину, которую Эйлер назвал моментом инерции. Понятие о моменте инерции расширилось: Эйлер умел уже находить моменты инерции относительно любой оси, он имел материал, соответствующий теореме о шести постоянных. Он ввел понятие о трех взаимно перпендикулярных главных осях, составил кубическое уравнение для определения их направлений и указал, что одна из них имеет наибольший, а другая — наименьший момент инерции. Он не знал только эллипсоида инерции, понятие о котором было введено потом Пуансо . Введенное им понятие о главных центральных осях позволило ему определить свободные оси вращения.
После этого Эйлер изучал общий случай движения тела. Он показал, что в таком движении можно выделить поступательную составляющую, которую удобнее всего относить к центру инерции. Движение, оставшееся после выделения поступательного, можно рассматривать как движение вокруг неподвижной точки. Для такого движения он доказал теорему Д ‘Аламбера , позволявшую утверждать, что движение тела с одной неподвижной точкой в каждый момент времени можно рассматривать как вращение вокруг некоторой оси.
Систему действующих на тело внешних сил он раскладывал на две силы, одна из которых проходит через центр инерции, a другая производит вращательное движение вокруг некоторой оси. Эту ось Эйлер уже не считал обязательно перпендикулярной к плоскости, проходящей через центр инерции и линию действия полученной первой силы, — ошибка, которую он сделал в 1740 г. при составлений первого тома «Морской науки».
Поэтому ставилась задача — определить направление оси вращения, проходящей через неподвижную точку, и соответствующую угловую скорость. Параллельно с этим он решал задачу: как изменится угловая скорость уже вращающегося твердого тела с неподвижной точкой, если к ней прибавить другую угловую скорость, которая получилась бы под действием момента, приложенного самостоятельно к рассматриваемому телу. Эта задаче понадобилась ему в связи с исследованием прецессии Земли.
После этих соображений общего характера Эйлер перешел к решению основной задачи и начал с простейшего случая, когда на рассматриваемое тело не действуют никакие внешние силы, а неподвижная точка совпадает с центром инерции. Он последовательно рассматривал три частных случая: когда тело имеет три равных главных центральных момента инерции, затем когда равны только два главных момента и, наконец, когда все три момента различны.
Первый случай его не затруднял: тело постоянно вращается с той угловой скоростью, которую оно получило в начальный момент. Во втором случае Эйлер нашел, что тело равномерно вращается вокруг некоторой подвижной оси, которая в свою очередь тоже равномерно вращается вокруг некоторой неподвижной оси, образуя с последней все время один и тот же угол; величина этого угла, а также величины двух получающихся угловых скоростей определяются начальными условиями (этот случай представляет то, что в настоящее время называется регулярной прецессией).
В самом общем случае Эйлер разбирался, но полученные им формулы оказались настолько сложными, что он остался неудовлетворенным.
В 1775 г. Эйлер нашел то решение, которое в настоящее время записывается в виде носящих его имя динамических дифференциальных уравнений.
Центр инерции тела, который после определения поступательного движения тела можно считать неподвижным, берется в качестве начала двух координатных систем, одна из которых неподвижна, а другая соединена с движущимся телом; координатные оси этой системы совпадают с главными осями инерции движущегося тела. Движение тела можно изобразить движением этой подвижной системы, положение которой определяется эйлеровыми углами φ ψ и Θ.
Пусть х, у, z — координаты точек тела в подвижной системе, а р , q, r —проекции угловой скорости тела на оси подвижной системы координат.
Выведенные Эйлером формулы для проекций скоростей имеют вид
dx dt = qz — ry ; dy dt = rx — pz ; dz dt = py — qx .
После дифференцирования этих формул получаем
d 2 x d t 2 = z dq dt — y dr dt + p qy + rz — x q 2 + r 2 ;
d 2 y d t 2 = x dq dt — z dr dt + q rz + px — y r 2 + p 2 ;
d 2 z d t 2 = y dp dt — x dq dt + r px + qy — z p 2 + q 2 ;
Принимаем, что эти уравнения написаны в подвижной системе координат; тогда в левой их части стоят проекции на оси подвижных координат ускорений точек с координатами х, у, z в подвижной системе; Если эти ускорения помножить на массы т каждой точки, то получим элементарную силу; действующую на эту точку. Составим моменты этих сил относительно подвижных осей координат. Образуем выражение
y d 2 z dt 2 — z d 2 y dt 2 = y 2 + z 2 dp dt — xy dq dt — xz dr dt + prxy — pqxz + rq y 2 — z 2 + yz r 2 — q 2 .
Помножив его на m, получим момент элементарной силы относительно оси х. Сумма всех таких моментов, распространенная на все тело, равна моменту внешних сил относительно оси х. Если оси подвижной системы координат являются главными центральными осями инерции, то суммы произведений вида тху , myz , тхz равны нулю и момент Мх внешних сил относительно подвижной оси О х
M x = Σm y 2 + z 2 dp dt + Σmqr y 2 — z 2 .
Σm y 2 + z 2 = A ; Σm z 2 + x 2 = B ; Σm x 2 + y 2 = C ,
M x = A dp dt — B — C qr .
M y = B dq dt — C — A rp ;
M z = C dr dt — A — B pq .
Таким образом, получены уравнения Эйлера. Интегрируя их, найдем зависимость составляющих р , q, r угловой скорости от времени t.
Кинематические уравнения Эйлера, определяющие параметры р , q, r через скорости dφ dt , dψ dt , dΘ dt 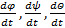
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
🔍 Видео
Динамика твердого тела. Тензор инерции. Уравнения ЭйлераСкачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

#225. КВАТЕРНИОНЫ и углы ЭйлераСкачать
Вывод уравнений движения идеальной жидкости - Лекция 2Скачать

Теорема Эйлера о движении жидкостиСкачать

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

06. Формула ЭйлераСкачать

Кугушев Е. И. - Аналитическая механика - Динамика твёрдого тела с неподвижной точкойСкачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Аналитическая механика 13. Динамика твердого тела. Случай Эйлера.Скачать

Форш П. А. - Теоретическая механика - Движение твердого тела. Углы ЭйлераСкачать

Общая физика | Лекция 18: Уравнение Эйлера. Гироскоп. Свободная и вынужденная прецессии.Скачать

Урок 93. Основное уравнение динамики вращательного движенияСкачать

Якута А. А. - Механика - Теорема Эйлера. Момент инерции. Тензор инерцииСкачать