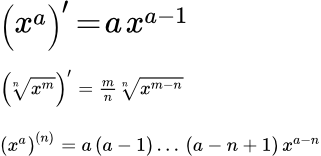Производная от степени квадратного уравнения (7 видео)

Содержание

Производная степенной функции (степени и корни)
Основные формулы
Вывод формулы производной степенной функции
Случай x > 0
Вывод формулы производной от корня степени n из x в степени m
Случай x = 0
Случай x . При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби: , где m и n – целые числа, не имеющие общего делителя.
Производные высших порядков
Примеры вычисления производных
Пример
Еще примеры
Квадратный трехчлен и его производная
Производная степенной функции
Формула
Примеры вычисления производной степенной функции
🔥 Видео

Видео:АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Производная степенной функции (степени и корни)

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Основные формулы

Производная от x в степени a равна a , умноженному на x в степени a минус один:
(1) .

Производная от корня степени n из x в степени m равна:
(2) .

Видео:4. Вычисление производных примеры. Самое начало.Скачать

Вывод формулы производной степенной функции

Случай x > 0

Рассмотрим степенную функцию от переменной x с показателем степени a :
(3) .
Здесь a является произвольным действительным числом. Сначала рассмотрим случай .

Чтобы найти производную функции (3), воспользуемся свойствами степенной функции и преобразуем ее к следующему виду:
.

Вывод формулы производной от корня степени n из x в степени m

Теперь рассмотрим функцию, являющуюся корнем следующего вида:
(4) .

Чтобы найти производную, преобразуем корень к степенной функции:
.
Сравнивая с формулой (3) мы видим, что
.
Тогда
.

На практике нет необходимости запоминать формулу (2). Гораздо удобнее сначала преобразовать корни к степенным функциям, а затем находить их производные, применяя формулу (1) (см. примеры в конце страницы).

Случай x = 0

Если , то степенная функция определена и при значении переменной x = 0 . Найдем производную функции (3) при x = 0 . Для этого воспользуемся определением производной:
.

Подставим x = 0 :
.
При этом под производной мы понимаем правосторонний предел, для которого .

Итак, мы нашли:
.
Отсюда видно, что при , .
При , .
При , .
Этот результат получается и по формуле (1):
(1) .
Поэтому формула (1) справедлива и при x = 0 .

Случай x .
При некоторых значениях постоянной a , она определена и при отрицательных значениях переменной x . А именно, пусть a будет рациональным числом. Тогда его можно представить в виде несократимой дроби:
,
где m и n – целые числа, не имеющие общего делителя.

Если n нечетное, то степенная функция определена и при отрицательных значениях переменной x . Например, при n = 3 и m = 1 мы имеем кубический корень из x :
.
Он определен и при отрицательных значениях переменной x .

Найдем производную степенной функции (3) при и при рациональных значениях постоянной a , для которых она определена. Для этого представим x в следующем виде:
.
Тогда ,
.
Находим производную, вынося постоянную за знак производной и применяя правило дифференцирования сложной функции:

.
Здесь . Но
.
Поскольку , то
.
Тогда
.
То есть формула (1) справедлива и при :
(1) .

Видео:Математика Без Ху!ни. Производная сложной функции.Скачать

Производные высших порядков

Теперь найдем производные высших порядков от степенной функции
(3) .
Производную первого порядка мы уже нашли:
.

Вынося постоянную a за знак производной, находим производную второго порядка:
.
Аналогичным образом находим производные третьего и четвертого порядков:
;

Отсюда видно, что производная произвольного n-го порядка имеет следующий вид:
.

Заметим, что если a является натуральным числом, , то n -я производная является постоянной:
.
Тогда все последующие производные равны нулю:
,
при .

Видео:4.2 Производная Примеры для тренировкиСкачать

Примеры вычисления производных

Пример

Найдите производную функции:
.

Преобразуем корни к степеням:
;
.
Тогда исходная функция приобретает вид:
.

Находим производные степеней:
;
.
Производная постоянной равна нулю:
.

Еще примеры

Найти производные следующих функций, зависящих от переменной x :
Решение > > > Решение > > > Решение > > > Решение > > > Решение > > >

Найти производную шестого порядка следующей функции:
.
Решение > > >

Автор: Олег Одинцов . Опубликовано: 09-04-2017

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Квадратный трехчлен и его производная

Разделы: Математика

Класс: 11

Цели урока:

Научить учащихся применять ранее полученные знания о квадратном трехчлене, линейной функции, производной, её геометрическом смысле в новой для них нестандартной ситуации;
Показать учащимся при решении задач естественную неразрывную связь между алгеброй и геометрией.
Формировать у учащихся навыки исследовательской работы.

Пособия:

слайды презентации PowerPoint с чертежами к уроку.

План урока:

Организационный момент;
Объявление темы урока, постановка целей урока;
Лекционное изложение нового материала с элементами закрепления:
Закрепление материала практическим решением нестандартных задач.
Итоги урока, постановка домашнего задания.

1. Организационный момент.

Приветствие учащихся. Сообщение темы, целей и плана урока.

2. Повторение свойств линейной и квадратичной функций;

По готовым слайдам презентации повторить свойства линейной и квадратичной функции.

3. Лекционная часть урока “Квадратный трехчлен и его производная”

Рассмотрим две функции: квадратный трехчлен и его производную , которая, очевидно, является линейной функцией. На рисунке 1 изображены их графики – парабола и прямая , которые иллюстрируют известный факт, что если на промежутке >0, то квадратный трехчлен на этом промежутке возрастает, если на промежутке ^ .

Касательная имеет вид . Чтобы найти нужно вычислить координаты точки А касания. Их нетрудно посчитать. Точка касания имеет координаты A, где . Составим уравнение касательной, зная угловой коэффициент и координаты точки касания, получим уравнение касательной . Это значит что . Теперь можно вычислить DF=. В прямоугольном треугольнике DCF острый угол равен углу между касательной и положительным направлением оси абсцисс, поэтому . Решая треугольник DCF находим СВ, а значит и искомое расстояние .

Задача 2. Как показано выше график квадратного трехчлена касается графика своей производной. Найдите координаты точки касания и докажите, что эта точка касания расположена всегда правее вершины параболы на одну единицу.

Решение. Координаты точки А касания посчитать нетрудно, А. Простой анализ координат точки А показывает, что абсцисса точки касания на единицу больше, чем абсцисса вершина параболы.

Задача 3. Парабола квадратного трехчлена и прямая , график его производной пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные с угловыми коэффициентами и. Докажите, что .

Решение. Абсциссы точек А и В пересечения параболы и прямой найдем из уравнения , , , ,

Найдем угловые коэффициенты и касательных, проведенные через точки А и В. Они равны значению функции в точках и , фактически эти значения совпадают с ординатами точек А и В. Вычислим их: , . Теперь ясно, что .

Еще один интересный момент. Если угловой коэффициент прямой АВ обозначить через , то учитывая, что , нетрудно установить удивительно простую зависимость между угловыми коэффициентами этих прямых: .

4. Практикум по решению задач.

Пусть

Производная от степени квадратного уравнения

некоторый квадратный трехчлен. Рассмотрим параболы

. Докажите, что вторая парабола получается из первой параллельным переносом на вектор

Последовательность квадратных трехчленов, задана реккурентным соотношением

. Докажите, что все параболы, являющиеся графиками функций из этой последовательности, имеют общую касательную.

Как продолжить последовательность функций из предыдущей задачи влево, если убрать ограничение

, то есть найдите квадратный трехчлен, непосредственно предшествующий квадратному трехчлену

Парабола

пересекает ось

в двух точках. Через каждую из них проведены касательные, которые пересекаются в точке С. Найдите координаты точки С.

Ответы к задачам: 3. ; 4. .

5. Самостоятельная работа в двух вариантах.

Вариант 1. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что: медиана СМ треугольника АВС параллельна оси ординат;

Вариант 2. Решите задачу:

Парабола и прямая пересекаются в двух точках А и В. К параболе через точки А и В проведены две касательные, которые пересекаются в точке С. Докажите, что одна из средних линий треугольника АВС является касательной к параболе .

6. Разбор задач самостоятельной работы

Разбор проводится по заранее подготовленным слайдам презентации PowerPoint. Оба варианта рассматриваются одновременно, потому что первая часть решения задач обоих вариантов одинакова, вторая же, различная часть, будет интересна учащимся обоих вариантов.

7. Задание на дом:

Рассмотрим четыре параболы

, где

– некоторый квадратный трехчлен. Докажите, что вершины этих парабол совпадают с вершинами некоторого квадрата.

Творческое задание (для желающих). Придумать свою задачу по теме “Квадратный трехчлен и его производная”

Видео:ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ решение производных функцийСкачать

Производная степенной функции

Видео:12. Производная степенно-показательной функцииСкачать

Формула

Производная степенной функции равна произведению показателя степени и основания в степени на единицу меньше.

Заметим, что в качестве степени 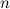может быть как натуральное число, то есть 1, 2, 3, . ; так и любое отрицательное число: — 1, — 2 и т.д., а также и любое дробное, например, 2,34; — 4,1 или $frac$ , $-frac$ .

Заметим, что если аргумент у степенной функции есть сложная функция (то есть там стоит более сложное выражение, чем просто $x$, то производную нужно находить по следующей формуле:

Видео:Производная степенной функцииСкачать