Уравнения движения тела под силы тяжести закон изменения скорости

Движение тела под действием силы тяжести является одной из центральных тем в динамической физике. О том, что раздел динамики базируется на трех законах Ньютона, знает даже обычный школьник. Давайте постараемся разобрать эту тему досконально, а статья, подробно описывающая каждый пример, поможет нам сделать изучение движения тела под действием силы тяжести максимально полезным.

Видео:Движение тела под действием силы тяжести. 1 часть. 9 класс.Скачать

Немного истории

Испокон веков люди с любопытством наблюдали за различными явлениями, происходящими в нашей жизни. Человечество долгое время не могло понять принципы и устройство многих систем, однако длительный путь изучения окружающего мира привел наших предков к научному перевороту. В наши дни, когда технологии развиваются с неимоверной скоростью, люди почти не задумываются о том, каким образом работают те или иные механизмы.

А между тем наши предки всегда интересовались загадками природных процессов и устройством мира, искали ответы на самые сложные вопросы и не переставали изучать, пока не находили на них ответы. Так, например, известный ученый Галилео Галилей еще в 16 веке задался вопросами: «Почему тела всегда падают вниз, какая же сила притягивает их к земле?» В 1589 году он поставил ряд опытов, результаты которых оказались весьма ценными. Он подробно изучал закономерности свободного падения различных тел, сбрасывая предметы со знаменитой башни в городе Пизе. Законы, которые он вывел, были улучшены и более детально описаны формулами еще одним известным английским ученым — сэром Исааком Ньютоном. Именно ему принадлежат три закона, на которых основана практически вся современная физика.

Тот факт, что закономерности движения тел, описанные более 500 лет назад, актуальны и по сей день, означает, что наша планета подчиняется неизменным законам. Современному человеку необходимо хотя бы поверхностно изучить основные принципы обустройства мира.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Основные и вспомогательные понятия динамики

Для того чтобы полностью понять принципы подобного движения, следует сначала ознакомиться с некоторыми понятиями. Итак, самые необходимые теоретические термины:

• Взаимодействие — это воздействие тел друг на друга, при котором происходит изменение или начало их движения относительно друг друга. Различают четыре вида взаимодействия: электромагнитное, слабое, сильное и гравитационное.
• Скорость — это физическая величина, обозначающая быстроту, с которой двигается тело. Скорость является вектором, то есть имеет не только значение, но также и направление.
• Ускорение — та величина, которая показывает нам быстроту изменения скорости тела в промежуток времени. Она также является векторной величиной.
• Траектория пути — это кривая, а иногда — прямая линия, которую очерчивает тело при движении. При равномерном прямолинейном движении траектория может совпадать со значением перемещения.
• Путь — это длина траектории, то есть ровно столько, сколько прошло тело за определенное количество времени.
• Инерциальная система отсчета — это среда, в которой выполняется первый закон Ньютона, то есть тело сохраняет свою инерцию, при условии, что полностью отсутствуют все внешние силы.

Вышеуказанных понятий вполне достаточно для того, чтобы грамотно начертить или представить в голове моделирование движения тела под действием силы тяжести.

Видео:Свободное падение тел. 10 класс.Скачать

Что значит сила?

Давайте перейдем к основному понятию нашей темы. Итак, сила — это величина, смысл которой заключается в воздействии или влиянии одного тела на другое количественно. А сила тяжести — это та сила, которая действует абсолютно на каждое тело, находящееся на поверхности или вблизи нашей планеты. Возникает вопрос: откуда же берется эта самая сила? Ответ заключается в законе всемирного тяготения.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

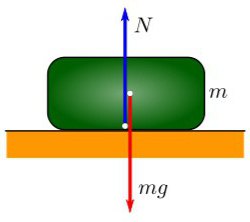
А что такое сила тяжести?

На любое тело со стороны Земли оказывает влияние гравитационная сила, которая сообщает ему некоторое ускорение. Сила тяжести всегда имеет вертикальное направление вниз, к центру планеты. Иначе говоря, сила тяжести притягивает предметы к Земле, вот почему предметы всегда падают вниз. Получается, что сила тяжести — это частный случай силы всемирного тяготения. Ньютон вывел одну из главных формул для нахождения силы притяжение между двумя телами. Выглядит она таким образом: F = G * (m₁ х m₂) / R 2 .

Видео:Урок 34. Свободное падение. Ускорение свободного паденияСкачать

Чему равно ускорение свободного падения?

Тело, которое отпустили с некоторой высоты, всегда летит вниз под действием силы притяжения. Движение тела под действием силы тяжести вертикально вверх и вниз можно описать уравнениями, где основной константой будет являться значение ускорения «g». Эта величина обусловлена исключительно действием силы притяжения, и ее значение приблизительно равно 9,8 м/с 2 . Получается, что тело, брошенное с высоты без начальной скорости, будет двигаться вниз с ускорением равным значению «g».

Видео:Уравнение движенияСкачать

Движение тела под действием силы тяжести: формулы для решения задач

Основная формула нахождения силы тяжести выглядит следующим образом: F_{тяжести} = m х g, где m — это масса тела, на которое действует сила, а «g» — ускорение свободного падения (для упрощения задач его принято считать равным 10 м/с 2 ).

Есть еще несколько формул, используемых для нахождения того или иного неизвестного при свободном движении тела. Так, например, для того чтобы вычислить пройденный телом путь, необходимо подставить известные значения в эту формулу: S = V₀ х t + a х t 2 / 2 (путь равен сумме произведений начальной скорости умноженной на время и ускорения на квадрат времени, деленной на 2).

Видео:9 класс. Движение тела под действием силы тяжести.Скачать

Уравнения для описания вертикального движения тела

Движение тела под действием силы тяжести по вертикали можно описать уравнением, которое выглядит так: x = x₀ + v₀ х t + a х t 2 / 2. Используя данное выражение, можно найти координаты тела в известный момент времени. Необходимо просто подставить известные в задаче величины: начальное местоположение, начальную скорость (если тело не просто отпустили, а толкнули с некоторой силой) и ускорение, в нашем случае оно будет равно ускорению g.

Таким же образом можно найти и скорость тела, которое движется под действием силы притяжения. Выражение для нахождения неизвестной величины в любой момент времени: v = v₀ + g х t (значение начальной скорости может быть равным нулю, тогда скорость будет равна произведению ускорения свободного падения на значение времени, за которое тело совершает движение).

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Движение тел под действием силы тяжести: задачи и способы их решений

При решении многих задач, связанных с силой тяжести, рекомендуем воспользоваться следующим планом:

1. Определить для себя удобную инерциальную систему отсчета, обычно принято выбирать Землю, потому как она отвечает многим требованиям к ИСО.
2. Нарисовать небольшой чертеж или рисунок, на котором изображены основные силы, действующие на тело. Движение тела под действием силы тяжести подразумевает набросок или схему, на которой указано, в каком направлении движется тело, если на него действует ускорение, равное g.
3. Затем следует выбрать направление для проецирования сил и полученных ускорений.
4. Записать неизвестные величины и определить их направление.
5. И наконец, используя указанные выше формулы для решения задач, вычислить все неизвестные величины, подставив данные в уравнения для нахождения ускорения или пройденного пути.

Видео:Физика 9 класс (Урок№1 - Движение тела, брошенного вертикально вверх)Скачать

Готовое решение легкой задачи

Когда речь идет о таком явлении, как движение тела под действием силы тяжести, определение того, каким способом практичнее решать поставленную задачу, может быть затруднительным. Однако есть несколько хитростей, используя которые, можно с легкостью решить даже самое сложное задание. Итак, разберем на живых примерах, как следует решать ту или иную задачу. Начнем с легкой для понимания задачи.

Некоторое тело отпустили с высоты 20 м без начальной скорости. Определить, за какое количество времени оно достигнет поверхности земли.

Решение: нам известен путь, пройденный телом, известно, что начальная скорость была равна 0. Также можем определить, что на тело действует только сила тяжести, получается, что это движение тела под действием силы тяжести, и поэтому следует воспользоваться этой формулой: S = V₀ х t + a х t 2 /2. Так как в нашем случае a = g, то после некоторых преобразований получаем следующее уравнение: S = g х t 2 / 2. Теперь осталось только выразить время через эту формулу, получаем, что t 2 = 2S / g. Подставим известные величины (при этом считаем, что g = 10 м/с 2 ) t 2 = 2 х 20 / 10 = 4. Следовательно, t = 2 с.

Итак, наш ответ: тело упадет на землю за 2 секунды.

Трюк, позволяющий быстро решить задачу, состоит в следующем: можно заметить, что описанное движение тела в приведенной задаче происходит в одном направлении (вертикально вниз). Оно весьма схоже с равноускоренным движением, так как на тело не действует никакая сила, кроме силы тяжести (силой сопротивления воздуха пренебрегаем). Благодаря этому можно воспользоваться легкой формулой для нахождения пути при равноускоренном движении, минуя изображения чертежей с расстановкой действующих на тело сил.

Видео:Теория движение тела брошенного вертикально вверхСкачать

Пример решения более сложной задачи

А теперь давайте посмотрим, как лучше решать задачи на движение тела под действием силы тяжести, если тело движется не вертикально, а имеет более сложный характер перемещения.

Например, следующая задача. Некоторый предмет массой m движется с неизвестным ускорением вниз по наклонной плоскости, коэффициент трения которой равен k. Определить значение ускорения, которое имеется при движении данного тела, если угол наклона α известен.

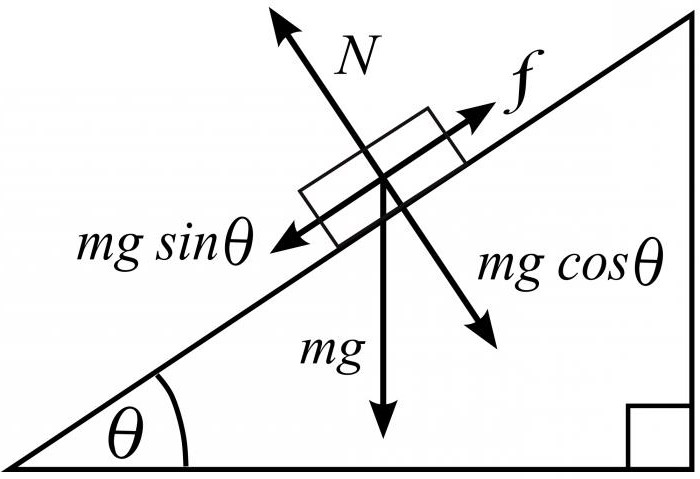
Решение: Следует воспользоваться планом, который описан выше. В первую очередь начертить рисунок наклонной плоскости с изображением тела и всех действующих на него сил. Получится, что на него действуют три составляющие: сила тяжести, трения и сила реакции опоры. Выглядит общее уравнение равнодействующих сил так: F_трения + N + mg = ma.

Главной изюминкой задачи является условие наклонности под углом α. При проецировании сил на ось ox и ось oy необходимо учесть данное условие, тогда у нас получится следующее выражение: mg х sin α — F_трения = ma (для оси ох) и N — mg х cos α = F_трения (для оси oy).

F_трения легко вычислить по формуле нахождения силы трения, она равна k х mg (коэффициент трения, умноженный на произведение массы тела и ускорения свободного падения). После всех вычислений остается только подставить найденные значения в формулу, получится упрощенное уравнение для вычисления ускорения, с которым движется тело вдоль наклонной плоскости.

Видео:Тема 19. Движение тела под действием силы тяжестиСкачать

Движение под действием силы тяжести

Подбросим мяч вертикально вверх. Он поднимется на какую-то высоту, после чего упадет вниз.

Земля притягивает мяч, значит на мяч действует нескомпенсированная сила притяжения. Как гласит второй закон Ньютона, скорость мяча из-за этого меняется.

Движение тела под действием силы тяжести, называется свободным падением. Когда тело падает свободно, оно испытывает невесомость.

Для удобства будем рассматривать отдельно свободное движение мяча вверх и, его свободное падение вниз.

Видео:Движение тела, брошенного под углом к горизонтуСкачать

Движение вверх

Рассмотрим рисунок 1. В левой части рисунка — 1а) изображено движение мяча вверх, а в правой – 1б) – движение вниз. Сплошным кружком обозначено начальное положение мяча, а пунктирным – конечное. Красными стрелками обозначена скорость мяча на различных высотах.

При движении вверх скорость тела уменьшается, так как вектор ускорения и вектор скорости направлены в противоположные стороны (рис. 1а). Движение вверх равнозамедленное.

Выражение для скорости при движении мяча вверх:

Вертикальное перемещение мяча при его движении вверх выражается такой формулой:

В верхней точке траектории скорость мяча будет равна нулю. Эта точка для движения вверх будет конечной, а для движения вниз – начальной.

Поэтому, для движения вверх нулю равна конечная скорость мяча (v_=0), а для движения вниз – его начальная скорость (v_=0).

Видео:Движение тела под действием силы тяжести. 2 часть. 9 класс.Скачать

Движение вниз

При движении вниз – наоборот, скорость будет увеличиваться, так как векторы скорости и ускорения сонаправлены (рис. 1б). Движение вниз равноускоренное.

Выражение для скорости при движении мяча вниз:

Вертикальное перемещение при движении вниз выражается формулой:

Таким образом, под действием силы тяжести мяч движется по вертикали, меняя свою скорость.

Пока мяч находится в полете, он не давит на опору и не растягивает подвес. Проще говоря, он находится в невесомости (ссылка) – то есть, не имеет веса.

Масса есть всегда, а вес тела (ссылка) может отсутствовать! Кроме того, одна и та же масса в различных ситуациях может обладать разным весом.

Из рисунка 1 так же, следует, что

если тело при падении вернется на уровень, с которого оно стартовало, то:

— скорость, с которой мы подбросим тело, по модулю будет равна скорости, с которой тело упадет ( large left|vec<v_> right|= left|vec<v_> right|) ;

— время подъема равняется времени спуска ( large t_<text> = t_<text> );

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Когда перемещение вверх не равно перемещению вниз

Рассмотрим теперь следующий рисунок. На рисунке 2а представлен случай, когда путь, пройденный вверх больше пути, пройденного при движении вниз. Предположим, мы подбросили мяч вертикально вверх и, он упал на крышу какого-то строения, например, гаража.

В таком случае на подъем потребуется больше времени, чем на спуск

И скорость, с которой мяч подбрасывали вверх будет больше скорости, с которой мяч ударится о крышу

На рисунке 2б путь при движении вверх меньше пути вниз. Такое может быть, если мы заберемся на крышу гаража и, находясь на крыше, подбросим мяч вертикально вверх.

Теперь на спуск мяча до земли потребуется больше времени, чем на подъем

Видео:Физика. 9 класс. Движение тела под действием силы тяжести /20.12.2020/Скачать

Закон всемирного тяготения. Движение тел под действием силы тяжести

Исходя из трактовки второго закона Ньютона, можно сделать вывод, что изменение движения происходит посредствам силы. Механика рассматривает силы различной физической природы. Многие из них определяются с помощью действия сил тяготения.

Видео:Физика. 9 класс. Движение тела под действием силы тяжести /25.12.2020/Скачать

Закон всемирного тяготения. Формулы

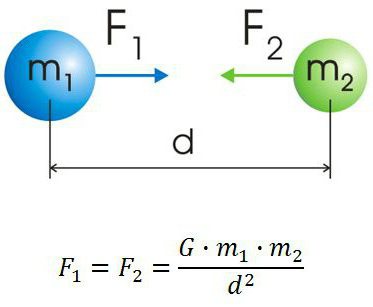
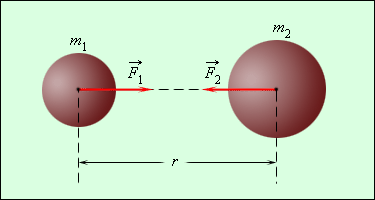
В 1862 году был открыт закон всемирного тяготения И. Ньютоном. Он предположил, что силы, удерживающие Луну, той же природы, что и силы, заставляющие яблоко падать на Землю. Смысл гипотезы состоит в наличии действия сил притяжения, направленных по линии и соединяющих центры масс, как изображено на рисунке 1 . 10 . 1 . Шаровидное тело имеет центр массы, совпадающий с центром шара.

Рисунок 1 . 10 . 1 . Гравитационные силы притяжения между телами. F 1 → = — F 2 → .

Далее, Ньютон искал физическое объяснение законам движения планет, которые открыл И. Кеплер в начале XVII века, и давал количественное выражение для гравитационных сил.

При известных направлениях движений планет Ньютон пытался выяснить, какие силы действуют на них. Этот процесс получил название обратной задачи механики.

Основная задача механики – определение координат тела известной массы с его скоростью в любой момент времени при помощи известных сил, действующих на тело, и заданным условием (прямая задача). Обратная же выполняется с определением действующих сил на тело с известным его направлением. Такие задачи привели ученого к открытию определения закона всемирного тяготения.

Видео:Физика - уравнения равноускоренного движенияСкачать

Ускорение свободного падения

Все тела притягиваются друг к другу с силой, прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.

F = G m 1 m 2 r 2 .

Значение G определяет коэффициент пропорциональности всех тел в природе, называемое гравитационной постоянной и обозначаемое по формуле G = 6 , 67 · 10 — 11 Н · м 2 / к г 2 ( С И ) .

Большинство явлений в природе объясняются наличием действия силы всемирного тяготения. Движение планет, искусственных спутников Земли, траектории полета баллистических ракет, движение тел вблизи поверхности Земли – все объясняется законом тяготения и динамики.

Проявлении силы тяготения характеризуется наличием силы тяжести. Так называется сила притяжения тел к Земле и вблизи ее поверхности.

Когда М обозначается как масса Земли, R З – радиус, m – масса тела, то формула силы тяжести принимает вид:

F = G M R З 2 m = m g .

Где g – ускорение свободного падения, равняющееся g = G M R З 2 .

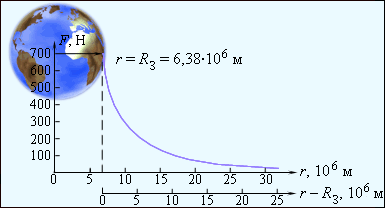
Сила тяжести направлена к центру Земли, как показано в примере Луна-Земля. При отсутствии действия других сил тело движется с ускорением свободного падения. Его среднее значение равняется 9 , 81 м / с 2 . При известном G и радиусе R 3 = 6 , 38 · 10 6 м производятся вычисления массы Земли М по формуле:

M = g R 3 2 G = 5 , 98 · 10 24 к г .

Если тело удаляется от поверхности Земли, тогда действие силы тяготения и ускорения свободного падения меняются обратно пропорционально квадрату расстояния r к центру. Рисунок 1 . 10 . 2 показывает, как изменяется сила тяготения, действующая на космонавта корабля, при удалении от Земли. Очевидно, что F притягивания его к Земле равняется 700 Н .

Рисунок 1 . 10 . 2 . Изменение силы тяготения, действующей на космонавта при удалении от Земли.

Земля-Луна подходит в качестве примера взаимодействия системы двух тел.

Расстояние до Луны – r Л = 3 , 84 · 10 6 м . Оно в 60 раз больше радиуса Земли R З . Значит, при наличии земного притяжения, ускорение свободного падения α Л орбиты Луны составит α Л = g R З r Л 2 = 9 , 81 м / с 2 60 2 = 0 , 0027 м / с 2 .

Оно направлено к центру Земли и получило название центростремительного. Расчет производится по формуле a Л = υ 2 r Л = 4 π 2 r Л T 2 = 0 , 0027 м / с 2 , где Т = 27 , 3 суток – период обращения Луны вокруг Земли. Результаты и расчеты, выполненные разными способами, говорят о том, что Ньютон был прав в своем предположении единой природы силы, удерживающей Луну на орбите, и силы тяжести.

Луна имеет собственное гравитационное поле, которое определяет ускорение свободного падения g Л на поверхности. Масса Луны в 81 раз меньше массы Земли, а радиус в 3 , 7 раза. Отсюда видно, что ускорение g Л следует определять из выражения:

g Л = G M Л R Л 2 = G M З 3 , 7 2 T 3 2 = 0 , 17 g = 1 , 66 м / с 2 .

Такая слабая гравитация характерна для космонавтов, находящихся на Луне. Поэтому можно совершать огромные прыжки и шаги. Прыжок вверх на метр на Земле соответствует семиметровому на Луне.

Видео:9 класс, 10 урок, Движение тела, брошенного вертикально вверхСкачать

Искусственные спутники Земли

Движение искусственных спутников зафиксировано за пределами земной атмосферы, поэтому на них оказывают действие силы тяготения Земли. Траектория космического тела может изменяться в зависимости от начальной скорости. Движение искусственного спутника по околоземной орбите приближенно принимается в качестве расстояния до центра Земли, равняющемуся радиусу R З . Они летают на высотах 200 — 300 к м .

Отсюда следует, что центростремительное ускорение спутника, которое сообщается силами тяготения, равняется ускорению свободного падения g . Скорость спутника примет обозначение υ 1 . Ее называют первой космической скоростью.

Применив кинематическую формулу для центростремительного ускорения, получаем

a n = υ 1 2 R З = g , υ 1 = g R З = 7 , 91 · 10 3 м / с .

При такой скорости спутник смог облететь Землю за время, равное T 1 = 2 πR З υ 1 = 84 м и н 12 с .

Но период обращения спутника по круговой орбите вблизи Земли намного больше, чем указано выше, так как существует различие между радиусом реальной орбиты и радиусом Земли.

Спутник движется по принципу свободного падения, отдаленно похожее на траекторию снаряда или баллистической ракеты. Разница заключается в большой скорости спутника, причем радиус кривизны его траектории достигает длины радиуса Земли.

Спутники, которые движутся по круговым траекториям на больших расстояниях, имеют ослабленное земное притяжение, обратно пропорциональное квадрату радиуса r траектории. Тогда нахождение скорости спутника следует по условию:

υ 2 к = g R 3 2 r 2 , υ = g R 3 R З r = υ 1 R 3 r .

Поэтому, наличие спутников на высоких орбитах говорит о меньшей скорости их движения, чем с околоземной орбиты. Формула периода обращения равняется:

T = 2 πr υ = 2 πr υ 1 r R З = 2 πR з υ 1 r R 3 3 / 2 = T 1 2 π R З .

T 1 принимает значение периода обращения спутника по околоземной орбите. Т возрастает с размерами радиуса орбиты. Если r имеет значение 6 , 6 R 3 то Т спутника равняется 24 часам. При его запуске в плоскости экватора, будет наблюдаться, как висит над некоторой точкой земной поверхности. Применение таких спутников известно в системе космической радиосвязи. Орбиту, имеющую радиус r = 6 , 6 R З , называют геостационарной.

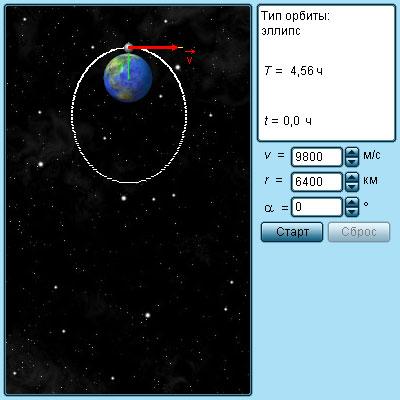
Рисунок 1 . 10 . 3 . Модель движения спутников.

🎦 Видео

Физика 9 класс (Урок№2 - Движение тела, брошенного горизонтально)Скачать

Физика. 9 класс. Движение тела под действием силы тяжести. Движение искусственных спутников ЗемлиСкачать