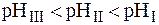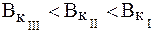Уравнения для расчета буферной емкости (6 видео)

Содержание

Рассчеты, связанные с приготовлением буферных растворов
Вычисление буферной емкости по кислоте
Вычисление рН буферного раствора
Расчет количества (моль) одноосновной кислоты
Буферные растворы
РН буферных растворов.
🎥 Видео

Видео:pH и буферные растворы | Медицинская химия | МедвузаСкачать

Рассчеты, связанные с приготовлением буферных растворов

Видео:Буферные системы, ацидоз и алкалоз, ур-ие Гендерсона-Гассельбаха (Атриум и Учим химию)Скачать

Вычисление буферной емкости по кислоте

Задача 51.
Какова буферная емкость по кислоте, если прибавление к 80 мл буферного раствора 30 мл 0,1 М раствора HCl вызвало изменение pH на единицу?
Решение:
Буферная емкость (buffer capacity) ß – число эквивалентов кислоты или щелочи, которое следует добавить к 1 л буферного раствора, чтобы изменить рН на единицу. Буферную емкость рассчитывают по уравнению:

ß = n/(z • V • ∆pH)

HCl — кислота одноосновная, поэтому z = 1:

n(HCl) = CV = 0,030 • 0,1 = 0,003 моль;
V(буфера) = 0,08 л
ß = 0,003/(1 • 0.08 • 1) = 0,0375 моль/л.

Ответ: ß = 0,0375 моль-экв/л.

Вычисление рН буферного раствора

Задача 52.
Вычислите рН раствора, полученного при смешивании 29 см 3 6,2 Н. раствора уксусной кислоты и 1 см 3 2,0 Н. раствора ацетата натрия.
Решение:
Получается буферный раствор — смесь слабой кислоты и ее соли (анионов слабой кислоты):

рН = рКа + lg[C_M(соли)/C_M(кислоты)];
C_M = С_H/z, где z — число эквивалентности.

Для кислоты z равно основности, для соли — числу катионов или анионов, умноженному на заряд соответствующего иона.
Уксусная кислота — одноосновная, поэтому z = 1.
В формуле ацетата натрия имеется по 1 иону с единичным зарядом, поэтому z = 1.
Соответственно, для обоих веществ С_Н = С_М.
При смешивании раствора получен буферный раствор объемом 29 + 1 = 30 мл = 0,03 л.

Ответ: рН = 6,71.

Расчет количества (моль) одноосновной кислоты

Задача 53.
Какое количество (моль) одноосновной кислоты необходимо ввести больному с рН крови 7,6 объемом 4л и буферной емкостью по кислоте 0,06 моль/л для нормализации рН крови?
Решение:
Установлено, что состоянию нормы соответствует определенный диапазон колебаний рН крови – от 7,37 до 7,44 со средней величиной 7,40. Рассчет будем производить по формуле:

ß = n/(z • V • ∆pH), где

ß — буферная емкость, n — количество вещества кислоты или соли, z — основность кислоты, V — объем раствора, ∆pH — изменене системы.

ß = 0,06 моль/л;
z = 1, потому что кислота одноосновная;
∆pH = (7,6 — 7,4) = 0,2;
V = 4л.

Рассчитаем количество (моль) одноосновной кислоты, получим:

ß = n/(z • V • ∆pH);
n(кислоты) = ß • (z • V • ∆pH) = 0,06 моль/л • (1 • 4 л •0,2) = 0,048 моль.

Ответ: n(кислоты) = 0,048 моль.

Видео:Буферные растворы. 1 часть. 11 класс.Скачать

Буферные растворы

Буферные растворы — это растворы, величина рН которых мало изменяется при добавлении к ним небольших количеств сильных кислот или щелочей, а также при разбавлении.

C точки зрения протонной теории простейший буферный раствор состоит из слабой кислоты и сопряженного ей основания или слабого основания и его сопряженной кислоты. В этом случае буферное действие растворов характеризуется наличием кислотно-основного равновесия:

Образуемые сопряженные кислотно-основные пары НА/А– и В/ВН+ называют буферными системами.

Классификация буферных систем

1. Кислотные. Состоят из слабой кислоты и соли этой кислоты. Например, ацетатная буферная система (CH3COOH+ СН3СООNa ), гидрокарбонатная буферная система (H2CO3 +NaHCO3 ).

2. Основные. Состоят из слабого основания и его соли. Например, аммиачная буферная система (NH3⋅H2O + NH4Cl).

3. Солевые. Состоят из кислой и средней соли или двух кислых солей. Например, карбонатная буферная система (NaHCO3+Na2CO3 ), фосфатная буферная система (КН2PO4 + К2НPO4).

4. Аминокислотные и белковые. Если суммарный заряд молекулы аминокислоты или белка равен нулю (изоэлектрическое состояние), то растворы этих соединений не являются буферными. Их буферное действие начинает проявляться тогда, когда к ним добавляют некоторое количество кислоты или щелочи. Тогда часть белка (аминокислоты) переходит из изоэлектрического состояния в форму “белок-кислота” или соответственно в форму “белок-основание”. Образуется смесь двух форм белка: а) слабая “белок-кислота” + соль этой слабой кислоты; б) слабое “белок — основание” + соль этого слабого основания:

где R — макромолекулярный остаток белка.

Расчет рН буферных систем

Для расчета рН в буферном растворе на примере ацетатного буфера рассмотрим процессы, в нем протекающие, и их влияние друг на друга.

Ацетат натрия практически полностью диссоциирует на ионы, ацетат-ион подвергается гидролизу, как ион слабой кислоты:

CH3COONa → Na+ + CH3COO–

CH3COO– + HOH ⇄ CH3COOH + OH–

Уксусная кислота, также входящая в буфер, диссоциирует лишь в незначительной степени:

CH3COOН ⇄CH3COO– + H+

Слабая диссоциация СН3СООН еще более подавляется в присутствии СН3СООNa, поэтому концентрацию недиссоциированной уксусной кислоты принимаем практически равной ее начальной концентрации:

С другой стороны, гидролиз соли также подавлен наличием в растворе кислоты. Поэтому можно считать, что концентрация ацетат-ионов в буферной смеси практически равна исходной концентрации соли без учета концентрации ацетат-ионов, образующихся в результате диссоциации кислоты:

Согласно закону действующих масс, равновесие между продуктами диссоциации уксусной кислоты и недиссоциированными молекулами подчиняется уравнению:

Кд = .

Подставив общую концентрацию кислоты и соли в уравнение константы диссоциации, получим: [Н+] = Кд,

отсюда для кислотных буферных систем: рН = рК(кислоты) + lg . Это уравнение называют уравнением Гендерсона – Гассельбаха.

рК — отрицательный десятичный логарифм константы диссоциации

После аналогичного вывода для основных буферных систем:

рОН = рК(основания) + lg , рН =14 – рК(основания) – lg

где рК(кислоты),рК(основания) — отрицательный десятичный логарифм константы электролитической диссоциации слабой кислоты; слабого основания; [соль] — концентрация соли, [кислота] — концентрация кислоты, [основание] — концентрация основания.

Из этих уравнений видно, что рН кислотной (основной) буферной системы зависит от природы слабого электролита (рК(кислоты), рК(основания)) и от соотношения концентраций соли и кислоты (основания).

Следует отметить, что буферные системы эффективно поддерживают рН в диапазоне: рК(кислоты)± 1 для кислотных систем; 14 – (рК(основания)± 1) для основных систем.

Механизм действия буферных систем:

1. Разбавление. При разбавлении водой происходит уменьшение концентрации обоих компонентов в буферной системе в одинаковой степени, поэтому величина их соотношения не изменится. рК(кислоты) и рК(основания) являются постоянными при данной температуре и не зависят от разбавления. Действительно, одновременное понижение концентраций кислоты и соли в ацетатной буферной системе от 0,1М до 0,001М при разбавлении водой изменяет рН буферного раствора с 4,63 до 4,73 (это ничтожное изменение рН при разбавлении буферного раствора в 100 раз обусловлено некоторым изменением коэффициента активности соли). Следовательно, разбавление в конечном итоге мало изменяет рН буферных систем.

2. Добавление кислот и оснований. При добавлении небольших количеств сильных кислот или оснований рН буферных систем изменяется незначительно. Например, рассмотрим ацетатный буфер:

кислотный компонент – основной компонент–

слабая кислота сопряженное основание

а) При добавлении к ацетатному буферу небольшого количества HCl, происходит взаимодействие ионов Н+ с основным компонентом буферного раствора:

Н+ + СН3СОО–⇄ СН3СООН.

Степень диссоциации СН3СООН мала и концентрация [H+] практически не меняется. рН буферного раствора уменьшится, но незначительно.

Таким образом, если к ацетатному буферу добавить Х моль/л HCl, то уравнение для расчета рН буферной системы принимает вид:

рН = рК(кислоты) + lg

б) При добавлении небольшого количества NaOH, – ионы нейтрализуются кислотным компонентом буферного раствора:

+ СН3СООН ⇄ СН3СОО – + Н2О.

В результате этого, добавленное сильное основание заменяется эквивалентным количеством слабого сопряженного основания (СН3СОО–), которое в меньшей степени влияет на реакцию cреды. рН буферного раствора увеличивается, но незначительно.

Таким образом, если к ацетатному буферу добавить У моль/л NaOH, то уравнение для расчета рН буферной системы принимает вид:

рН = рК(кислоты) + lg

Способность буферного раствора сохранять значение рН при добавлении сильной кислоты или щелочи приблизительно на постоянном уровне характеризует буферная емкость.

Буферная емкость (В) — это число молей эквивалента сильной кислоты или щелочи, которое необходимо добавить к 1 л буферного раствора, чтобы сместить его рН на единицу.

Буферная емкость системы определяется по отношению к добавляемым кислоте (Вкисл.) или основанию (щелочи) (Восн.) и рассчитывается по формулам:

Вкисл.= Восн.=

где V(HA), V(B) — объемы добавленных кислоты или щелочи, л.; Сн(НА), Сн(В) — молярные концентрации эквивалента соответственно кислоты и щелочи; V(б. р.) — объем исходного буферного раствора, л.; рНо, рН — значения рН буферного раствора до и после добавления кислоты или щелочи; |рН-рНо| — разность рН по модулю.

Буферная емкость по отношению к кислоте (Вкисл.) определяется концентрацией (количеством эквивалентов) компонента с основными свойствами; буферная емкость по отношению к основанию (Восн.) определяется концентрацией (количеством эквивалентов) компонента с кислотными свойствами в буферном растворе.

Максимальная буферная емкость при добавлении сильных кислот и оснований достигается при соотношении компонентов буферного раствора равном единице, когда рН = рК, при этом Восн.= В кисл. (рис.1).Поэтому, применение любой буферной смеси ограничено определенной областью рН (областью буферирования), а именно:

рН = рК(кислоты)± 1 для кислотных систем, или

рН= 14 – (рК(основания)± 1) для основных систем.

Буферная емкость зависит не только от отношения концентраций компонентов буферного раствора, но и от общей концентрации буферной смеси.

Рис.1. Изменение буферной емкости в зависимости от величины отношения [соль]/[кислота].

Пусть, например, даны два буферных раствора, один из которых содержит по 100, а другой – по 10 миллимолей уксусной кислоты и ацетата натрия. Сравним, как изменяются их рН при добавлении к 1 л каждого раствора 5 миллимолей соляной кислоты.

Добавляемая кислота вступит в реакцию с ацетатом натрия, и это отношение в первом растворе станет равным 0,9, а во втором 0,33. В итоге у первого раствора отношение соль/кислота и, следовательно, величина рН изменились меньше. Отсюда видно, что первый буферный раствор обладает большей буферной емкостью.

Таким образом, буферная емкость в основном зависит от соотношения концентраций компонентов и их абсолютных концентраций, а следовательно, от разбавления.

Буферные системы организма

Главным источником ионов водорода в организме является углекислый газ, образующийся в результате метаболизма (обмена веществ) ≈ 15000 ммоль/сутки.

Гидратация углекислого газа приводит к образованию угольной кислоты:

СО2 + Н2О ⇄ Н2СО3⇄ + Н+

В меньшей степени количество ионов Н+ (30–80 ммоль/сутки) обусловлено поступлением в организм, а также образованием в нем таких кислот как серной (в результате обмена серусодержащих аминокислот), фосфорной (при метаболизме фосфорсодержащих соединений), органических кислот, образующихся при неполном окислении липидов и углеводов.

Организм освобождается от кислот благодаря процессам дыхания и мочевыделения, т. е. в организме существует взаимосвязь между метаболическими процессами и газообменом. В оценке кислотно-основного состояния организма важно не только определение значения рН, но и характеристика механизмов, обеспечивающих регуляцию этого параметра.

Если бы в организме не было немедленных буферных механизмов и респираторной (дыхательной) компенсации, то тогда даже обычные, ежедневные нагрузки кислотами сопровождались бы значительными колебаниями величины рН.

Постоянство рН жидких сред организма поддерживается в живых организмах буферными системами. Главным из них являются гидрокарбонатная, гемоглобиновая, фосфатная и белковая. Действие всех буферных систем в организме взаимосвязано, что обеспечивает биологическим жидкостям постоянное значение рН. В организме человека и животных буферные системы находятся в крови (плазме и эритроцитах), в клетках и межклеточных пространствах других тканей.

Буферные системы крови представлены буферными системами плазмы крови и буферными системами эритроцитов. Буферные системы плазмы – гидрокарбонатная, белковая и фосфатная, роль последней незначительна. На их долю приходится ≈ 44% буферной емкости крови. Буферные системы эритроцитов – гемоглобиновая, гидрокарбонатная, система органических фосфатов (фосфатная). На их долю приходится ≈ 56% буферной емкости крови.

Видео:Расчёты pH буферных растворов (видео 5) | Буферные растворы | ХимияСкачать

РН буферных растворов.

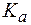
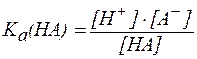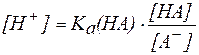Для буферной системы I типа НА/A — концентрацию ионов Н + в растворе легко вычислить, исходя из константы диссоциации слабой кислоты (для простоты изложения вместо активностей ионов в выражении для будем использовать их концентрации):

В присутствии второго компонента буферного раствора – сильного электролита – равновесие диссоциации слабой кислоты НA, согласно принципу Ле Шателье, смещено влево. Поэтому можно считать, что концентрация недиссоциированных молекул НA практически равна концентрации кислоты в буферном растворе, а концентрация ионов A — равна концентрации соли.

В таком случае можно записать:

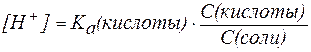(3)

где С(кислоты) и С(соли) – молярные концентрации кислоты и соли.

Если равенство (3) прологарифмировать (взять отрицательный десятичный логарифм левой и правой частей уравнения), то получим:

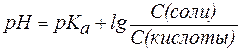(4)

Так, рН фосфатной буферной системы состава NaH₂PO₄/Na₂HPO₄ можно рассчитать по уравнению:

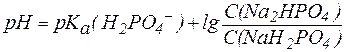где 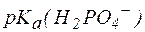– показатель константы диссоциации фосфорной кислоты по второй ступени.

В случаях, когда требуется получить буферный раствор с задан-ным значением pH, используют уравнение:

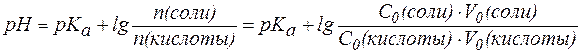(5)

где индексом «0» обозначены характеристики исходных растворов кислоты и соли, смешиванием которых получают требуемую буферную смесь.

Для буферной системы II типа В/ВН + , например аммонийной, гидроксидный и водородный показатели вычисляют по уравнениям:

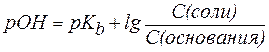,	(6)
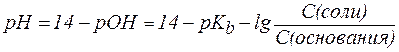,	(6¢)

где 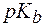– показатель константы диссоциации основания.

В общем виде уравнение для расчета pH буферных систем выглядит следующим образом:

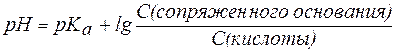(7)

и называется уравнениемГендерсона-Гассельбаха.

Из уравнения Гендерсона-Гассельбаха следует, что:

1. Величина рН буферных растворов зависит от константы диссоциации кислоты или основания и от соотношения количеств компонентов, но практически не зависит от разбавления или концент-рирования растворов. Действительно, в этих процессах концентрации компонентов буферного раствора изменяются пропорционально, поэтому их соотношение, которое определяет значение рН буферного раствора, остается неизменным.

Если концентрации компонентов буферных растворов превы-шают 0,1 моль/л, то в расчетах необходимо учитывать коэффициенты активности ионов системы.

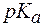
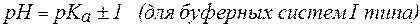
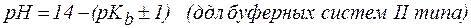
2. Показатель константы диссоциации слабого электролита опре-деляет область буферного действия раствора, т.е. тот интервал значе-ний водородного показателя, в котором сохраняются буферные свой-ства системы. Поскольку буферное действие продолжается, пока не израсходовано 90% компонента (т.е. его концентрация не уменьши-лась на порядок), то область (зона) буферного действия отличается от на 1 единицу:

;

Амфолиты могут иметь несколько зон буферного действия, каждая из которых отвечает соответствующей константе :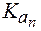

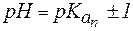
Таким образом, максимально допустимое соотношение компонентов раствора, при котором он проявляет буферное действие, составляет 10:1.

Пример 1. Можно ли приготовить ацетатный буфер с рН = 6,5, если 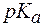уксусной кислоты равен 4,74?

Поскольку зона буферного действия определяется как 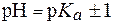, для ацетатного буфера она находится в интервале значений рН от 3,74 до 5,74. Значение рН = 6,5 лежит за пределами зоны действия ацетатного буфера, поэтому на основе ацетатной буферной системы такой буфер приготовить нельзя.

Буферная емкость.

Прибавлять кислоту или щелочь, существенно не меняя рН буферного раствора, можно лишь в относительно небольших коли-чествах, так как способность буферных растворов сохранять постоян-ство рН ограничена.

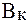
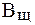
Величина, характеризующая способность буферного раствора противодействовать смещению реакции среды при добавлении кислот и щелочей, называется буферной емкостью (В).Различают буферную емкость по кислоте ( ) и по щелочи ( ).

Буферная емкость (В) измеряется количеством кислоты или щелочи (моль или ммоль эквивалента), добавление которого к 1 л буферного раствора изменяет рН на единицу.

На практике буферную емкость определяют титрованием. Для этого определенный объем буферного раствора титруют сильной кислотой или щелочью известной концентрации до достижения точки эквивалентности. Титрование проводят в присутствии кислотно-основных индикаторов, при правильном выборе которых фиксируют состояние, когда компонент буферной системы прореагирует полностью. 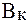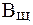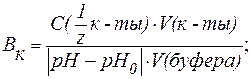По полученным результатам рассчитывают величину буферной емкости ( или ):

	(8)
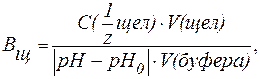	(9)

где С( к-ты), С( щел) — молярные концентрации эквивалента кислоты и щелочи (моль/л);

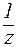
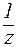
V(к-ты ), V(щел) — объемы добавленных растворов кислоты или щелочи (л; мл);

V(буфера) — объем буферного раствора (л; мл);

pH₀ и pH — значения рН буферного раствора до и после титрования кислотой или щелочью (изменение рН берется по абсолютной величине).

Буферную емкость выражают в [моль/л] или в [ммоль/л].

Буферная емкость зависит от ряда факторов:

1. Чем больше абсолютное содержание компонентов пары основание/сопряженная кислота, тем выше буферная емкость буфер-ного раствора.

Буферная емкость зависит от соотношения количеств компо-нентов буферного раствора, а следовательно, и от рН буфера. Буфер-ная емкость максимальна при равных количествах компонентов бу-ферной системы и уменьшается с отклонением от этого соотношения.

3. При различном содержании компонентов буферные емкости раствора по кислоте и по щелочи отличаются. Так, в буферном растворе I типа чем больше содержание кислоты, тем больше буферная емкость по щелочи, а чем больше содержание соли, тем больше буферная емкость по кислоте. В буферном растворе II типа чем больше содержание соли, тем больше буферная емкость по щелочи, а чем больше содержание основания, тем больше буферная емкость по кислоте.

Пример 2. Для приготовления ацетатных буферных смесей растворы кислоты и соли одинаковой молярной концентрации были смешаны в следующих объемных соотношениях:

Состав буферной системы	Объемные соотношения компонентов буферной системы
раствор I	раствор II	раствор III
CH₃COOH
CH₃COONa

Не прибегая к расчетам, определить, в каком из трёх буферных растворов будет наблюдаться:

а) наибольшее значение рН;

б) максимальная буферная емкость;

в) наибольшая буферная емкость по кислоте.

В случае равных концентраций компонентов уравнение (5) принимает вид:

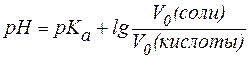
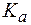
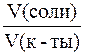
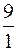
Так как во всех трех растворах одинакова, то значение pH буфера будет определяться соотношением . Следовательно, наибольшим значением pH будет обладать I раствор ( ):

Максимальной буферной емкостью характеризуется II раствор, так как в нем соотношение количеств компонентов составляет 1:1.

Буферная емкость по кислоте для ацетатного буфера определя-ется содержанием сопряженного основания, т.е. соли: чем оно больше, тем больше буферная емкость раствора по кислоте. Поэтому: