Уравнения баланса энергии и импульса

Множество непонятных свойств мира связаны с природой массы и энергии (а также импульса). Все мы слышали эти слова и у многих из нас есть туманное представление об их значении. Конечно, значений у слов «масса» и «энергия» в английском и других языках довольно много. К сожалению, ни одно из них не совпадает с теми, что имеют в виду физики. Попробуйте отставить в сторону эти значения слов и поработать с точными физическими понятиями – иначе вы полностью запутаетесь.

Необходимо отметить, что не стоит при словосочетании «масса и энергия» вспоминать другую популярную пару, «вещество и энергия». Многие люди упоминают последнее словосочетания так, будто вещество и энергия – это две стороны одной медали. Но это не так. Вещество и энергия относятся к разным категориям, как яблоки и орангутанги. Вещество, не важно, как его определять – это класс объектов, существующих во Вселенной, а масса и энергия – это не объекты, а свойства, которыми эти объекты обладают. Масса и энергия глубоко переплетены друг с другом, и заслуживают общего объяснения.

Чтобы понять массу и энергию, необходимо добавить к ним импульс и обсудить различия и связи этих величин.

Видео:Закон сохранения превращения энергии в тепловых процессах. 8 класс.Скачать

Энергия

У слова «энергия» есть множество значений. Когда мы заболеваем, то говорим о том, что у нас не осталось энергии, имея в виду силу и мотивацию. Когда мы говорим, что у кого-то полно энергии, мы имеем в виду его высокую активность. Мы жалуемся на рост цен на энергию, имея в виду топливо. Мы говорим о духовной энергии как о чём-то неизмеримом, но важном, возможно, о некоей форме харизмы. И все эти понятия перекликаются друг с другом, поэтому мы и выбираем одно слово для их описания. Но в физике энергия – это совсем другое. С точки зрения физики ошибочно будет смешивать одно из этих определений с физическим. В физике нужно придерживаться физического термина, чтобы не получить неправильные ответы и не запутаться вконец.

К несчастью, понятие «энергии» в физике очень сложно описать так, как это делают словари – короткой содержательной фразой. Но не подумайте плохого – всё дело в несовершенстве естественного языка, а не в том, что понятие энергии в физике расплывчато. В любой заданной физической системе совершенно понятно, какова её энергия, как в смысле её экспериментального измерения, так и в смысле расчётов (при наличии описывающих систему уравнений).

Одна из причин, по которым энергию так сложно описать – она может принимать множество форм, и не все из них просто понять. Вот три наиболее часто встречающихся разновидности:

1. Энергия может быть заключена в массе объекта. Здесь я называю такой вариант «энергией массы» (благодаря известному уравнению E=mc 2 энергия связывается с массой. Также она называется «энергия покоя», поскольку это энергия объекта, находящегося в покое, то есть, без движения).

2. Во-вторых, энергия бывает связанной с движением объекта. Здесь я называю её «энергией движения», а технический термин для этого – кинетическая энергия. Этот вариант интуитивно легко воспринять, поскольку у быстро движущихся объектов энергия больше, чем у медленно движущихся. Кроме того, у тяжёлого объекта энергия движения больше, чем у лёгкого, движущегося с той же скоростью.

3. Энергия может храниться во взаимоотношении объектов (и обычно называется «потенциальной»). Она хранится в растянутой пружине, в воде за дамбой, в гравитационном взаимодействии Земли и Солнца, во взаимодействиях атомов в молекуле. Существует множество способов хранения энергии. Звучит расплывчато, но в этом виноват язык. В любом из перечисленных случаев существуют точные формулы, описывающие сохранённую в системе энергию и хорошо определённые пути её измерения.

С третьим типом энергии связано то, что я буду называть энергией взаимодействия, и это наиболее запутанное понятие из всех. В отличие от энергии массы и энергии движения, которые всегда больше или равны нулю, энергия взаимодействий может быть положительной и отрицательной. Пока я оставлю эту тему, но мы к ней ещё вернёмся.

Энергия – это особая величина огромной важности для физики. Причина такой важности – в том, что она «сохраняется». Что же это означает?

Если вы начнёте наблюдение с объекта или с набора объектов – назовём их «системой объектов» – обладающих определённым количеством энергии в начальный момент (не забудьте подсчитать всю энергию – массы, движения, сохранённую энергию всех типов, и т.п.), а затем части системы будут взаимодействовать только друг с другом и более ни с чем, тогда в конце наблюдения общее количество энергии, которым обладают эти объекты, будет тем же, что и в начале. Общая энергия системы сохраняется – её общее количество не меняется. Она может менять форму, но если отслеживать все разновидности, то в конце её будет столько же, сколько и в начале.

Это правило работает, даже если некоторые объекты будут исчезать и уступать место другим, к примеру, если одна частица в системе распадётся на две других, вливающихся в систему.

Почему энергия сохраняется? Из-за математического принципа, соотносящего тот факт, что законы природы со временем не меняются, с существованием сохраняющейся величины, которую мы по определению называем «энергией».

Самым известным и общим определением этого принципа мы обязаны Эмми Нётер, одной из величайших математических физиков предыдущего столетия, современнице Эйнштейна. Некоторые члены физического и математического сообщества относились к ней с глубоким уважением, но в то время в своей родной Германии она страдала от дискриминации по половому и национальному признаку (там блокировали попытки присвоить ей звание профессора в Гёттингене, и оттуда ей пришлось бежать после того, как к власти пришли нацисты). Эмигрировав в США, всего после двух лет преподаваний в колледже Брин-Мар (который по сию пору принимает для обучения только женщин), она умерла от онкологического заболевания.

Знаменитая теорема Нётер (реально это две тесно связанных теоремы) говорит нам, что если в законах природы существует симметрия – в нашем случае это значит, что законы природы одинаковы в любой момент времени – то из этого следует сохранение некоей величины – в нашем случае, энергии.

Более того, теорема в точности сообщает нам, что это за величина – каковы различные формы энергии, для заданной системы объектов, которые необходимо сложить, чтобы получить общую энергию. Именно поэтому физики всегда точно знают, что такое энергия, и почему её легче получить при помощи уравнений, чем определить словами.

Видео:Урок 104. Импульс. Закон сохранения импульсаСкачать

Импульс

С импульсом дело обстоит примерно таким же образом, что и с энергией. Законы природы везде одинаковые. Грубо говоря, эксперименты дают одни и те же ответы, проводите ли вы их к северу или к югу отсюда, к западу или востоку, на вершине здания или в глубокой шахте. Выберите любое направление в пространстве. Тогда, согласно Нётер, импульс вдоль этого направления сохраняется. Поскольку в пространстве есть три измерения, то можно двигаться в трёх разных независимых направлениях и существуют три независимых закона сохранения. Выбрать можно три любых направления, при условии, что они разные. К примеру, можно выбрать в качестве трёх законов сохранения импульсы в направлениях север-юг, запад-восток и вверх-вниз. Или можно выбрать три других – по направлению к и от Солнца, вдоль орбиты Земли в обе стороны, и вверх и вниз по отношению к плоскости Солнечной системы. Ваш выбор не имеет значения, ибо импульс сохраняется вдоль любого направления.

Простейшая форма импульса возникает благодаря простому движению объектов, и это примерно то, что можно представить себе интуитивно: если объект двигается в определённом направлении, то у него есть импульс в этом направлении, и чем быстрее он двигается, тем больше этот импульс. А у более тяжёлого объекта импульс больше, чем у лёгкого, если они двигаются с одинаковыми скоростями.

Одно из интересных следствий этого сохранения: если у вас имеется неподвижная система из объектов (то есть, система в целом не двигается, если усреднить все движения составляющих её объектов), тогда она будет оставаться неподвижной, если только ей не придаст движение какое-либо внешнее воздействие. Причина в том, что у неподвижной системы суммарный импульс равен нулю, и поскольку импульс сохраняется, он останется равным нулю навсегда, если только не вмешается что-либо извне системы.

Видео:Физика - импульс и закон сохранения импульсаСкачать

Масса, и её связь с энергией и импульсом

Теперь обратимся к массе

К сожалению, с массой связано много путаницы – после выхода работы Эйнштейна по теории относительности некоторое время существовало два понятия массы. И только одно из них (то, на котором остановился сам Эйнштейн, и которое иногда называют «инвариантной массой» или «массой покоя», чтобы отличить её от уже ставшего архаичным термина «релятивистская масса»), до сих пор используют в физике частиц. В отдельной статье я поясню это более подробно.

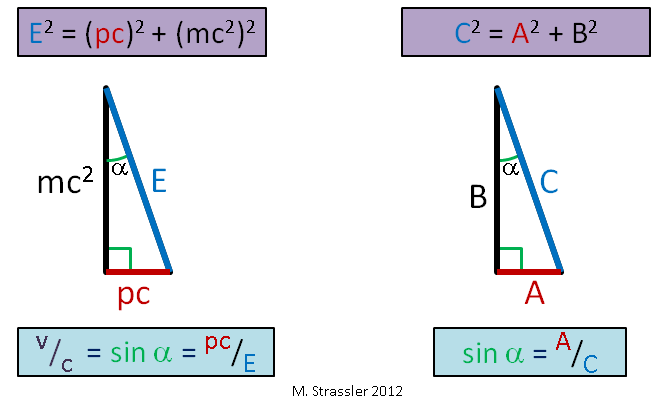
Рис. 1

Под массой m, которую я использую в статьях, подразумевается та масса, что непосредственно связывает энергию и импульс. Для объекта, двигающегося без воздействия внешних сил (не взаимодействующего значительно с другими объектами), Эйнштейн предположил (и это было подтверждено экспериментами), что его энергия E, импульс p и масса m удовлетворяют простому пифагорову равенству:

Помните старика Пифагора, утверждавшего, что для прямоугольного треугольника со сторонами A и B и гипотенузой C выполняется равенство ? Это связь того же типа – см. рис. 1. У нас с – постоянная скорость, которая, как мы увидим, служит универсальным пределом скорости. Также мы увидим, почему её называют «скоростью света».

Согласно уравнениям Эйнштейна, скорость объекта, делённая на предел скорости с, это просто отношение pc к Е:

То есть отношение горизонтального катета к гипотенузе. Оно также равно синусу угла α на рис. 1. Вот так вот, граждане. А поскольку катеты прямоугольного треугольника всегда короче гипотенузы (синус любого угла всегда меньше или равен 1), скорость любого объекта не может превышать с, универсальный предел скорости. С увеличением скорости объекта фиксированной массы p и E становятся очень большими (рис. 2), но E всегда больше pc, поэтому v всегда меньше c!

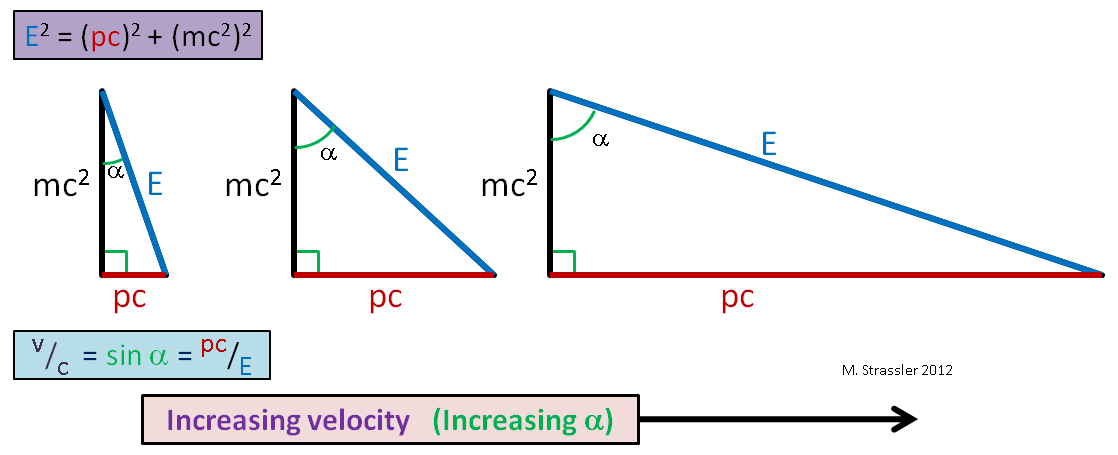
Рис. 2

Теперь обратите внимание, что если объект не двигается, то его импульс p равен нулю, и отношение в уравнении 1 сводится к:

Знаменитая формула Эйнштейна, связь массы с фиксированным количеством энергии (то, что я называю энергией массы), это просто утверждение, соответствующее тому, что когда треугольник вырождается в вертикальную линию, как на рис. 3 слева, его гипотенуза становится такой же длины, как вертикальный катет. При этом оно не означает, что энергия всегда равна массе, помноженной на квадрат с. Это работает только для покоящегося объекта с нулевым импульсом.

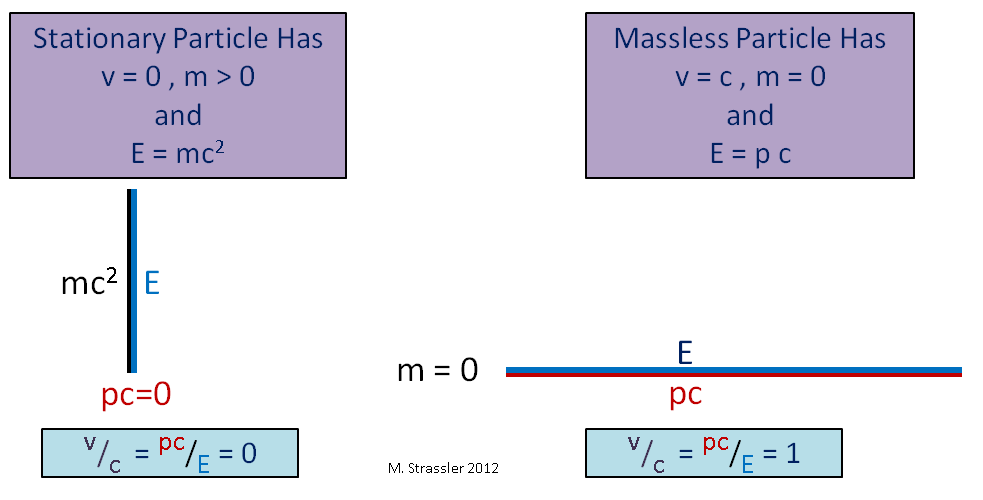
Рис. 3

Ещё одно интересное наблюдение: для безмассовой частицы вертикальный катет треугольника нулевой, а гипотенуза и горизонтальный катет совпадают, как на рис. 3. В таком случае E равняется pc, что означает, что v/c = 1, или v = c. Видно, что безмассовая частица (к примеру, фотон, частица света) неизбежно перемещается со скоростью с. Поэтому скорость света такая же, как универсальный предел скорости, с.

С другой стороны, если взять обладающую массой частицу, как на рис. 4, то неважно, насколько большим вы делаете импульс и энергию, E всегда будет немного больше, чем p*c, поэтому скорость всегда будет меньше с. Безмассовые частицы обязаны перемещаться с максимальной скоростью. Скорость массивных частиц должна быть меньше.

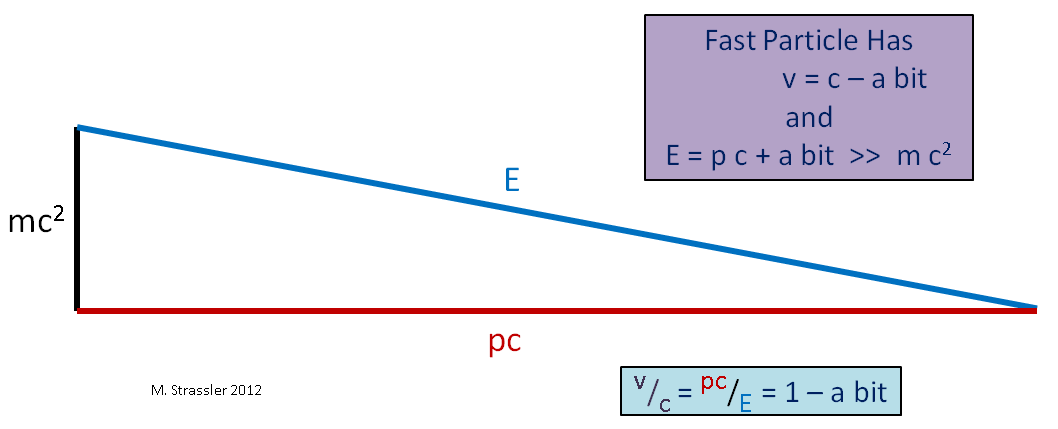
Рис. 4. Здесь «>>» означает «гораздо больше»

Представьте себе другой пограничный случай, медленно (по сравнению со скоростью света) движущийся массивный объект, к примеру, автомобиль. Поскольку его скорость v гораздо меньше с, его импульс p умноженный на c будет гораздо меньше E, и, как видно из рис. 5, E будет немногим больше, чем mc 2 . Поэтому энергия движения медленного объекта E — mc 2 гораздо меньше, чем энергия его массы mc 2 , а у быстрого объекта энергию движения можно сделать сколь угодно большой, как мы видели на рис. 4.

Один тонкий момент: импульс – это не только число, но и вектор. У него есть величина и направление. Он направлен в сторону движения частицы. Когда я пишу «p», я указываю только величину. Во многих случаях необходимо отслеживать и направление импульса, хотя в уравнении №1, связывающем импульс с энергией и массой, этого делать не нужно.

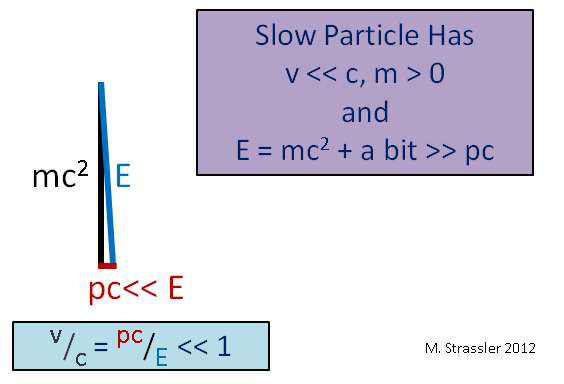
Рис. 5

Ещё один тонкий момент: я использовал треугольники и простейшую тригонометрию, поскольку она известна всем из школы. Экспертам же нужно быть осторожнее – правильно понять уравнения Эйнштейна можно, используя гиперболические функции, обычно не встречающиеся дилетантам, но крайне важные для понимания структуры теории, и делающие более понятными такие вещи, как сложение скоростей, сжатие расстояний и т.п. Не претендующие на экспертизу люди могут это игнорировать.

Видео:Закон сохранения импульсаСкачать

Но скорость же относительна.

Если вы внимательно читали текст, вас уже может кое-что удивить. Вы знаете, что скорость частицы – или чего угодно, движущегося медленнее света – зависит от точки зрения.

Если вы сидите дома и читаете книгу, вы скажете, что скорость книги нулевая (и относительно вас она действительно покоится), следовательно, у неё нет импульса и энергии движения, только энергия массы. Но если бы я стоял на Луне, то я напомнил бы вам, что Земля вертится, поэтому это вращение увлекает и вас, и двигает вас относительно меня со скоростью в сотни километров в час. Так что вы с вашей книгой обладали бы импульсом с моей точки зрения.

Вариант относительности согласно Галилею – первый принцип относительности – утверждает, что правы мы оба. Вариант относительности Эйнштейна соглашается с точкой зрения Галилея в том, что правы оба, но вносит важные корректировки в то, как обозначили бы последователи Галилея энергию, импульс и массу книги, помещая эти величины в пифагорово соотношение уравнения №1.

Но если правы все, какую E и какой p мне нужно подставить в соотношение энергии/импульса/массы, ? Подставить E и p, измеренные вами, читающим книгу, то есть E = mc 2 и p = 0? Или подставить E и p, которыми обладает книга с моей точки зрения, когда вы двигаетесь вместе с Землёй?

В ответе на этот вопрос содержится вся суть уравнения Эйнштейна №1. Каждый наблюдатель измерит разные величины E и p для книги, в зависимости от того, как быстро книга будет двигаться относительно него. Но для всех наблюдателей уравнение будет верным!

Магия! А на самом деле, гениальность – мысль, пришедшая в 1905 году, о том, как можно заменить набор уравнений, предложенных Ньютоном и его последователями, новым удивительным набором уравнений, всё ещё совпадающим со всеми предыдущими экспериментами, но оказавшимся более точным представлением реальности. Сложно представить, как сильно нужно было изменить образ мышления, чтобы додуматься до этого, пока не разберёшься с тем, сколько всего во время формирования новой теории могло пойти не так, и сколько других различных уравнений, содержащих противоречия с математикой или с предыдущими экспериментами, можно было бы предложить (а люди их предлагали). Мне, к примеру, постоянно приходят работы начинающих физиков, пытающихся «исправить» уравнения Эйнштейна, но я никогда не видел, чтобы кто-нибудь из них проверил свои уравнения на внутреннюю непротиворечивость. Это очень сложная задача и причина неудачи большинства теорий.

Видео:ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ в механике класс физика ПерышкинСкачать

Но как тогда могут сохраняться энергия и импульс?

Погодите-ка, – скажете вы, когда ваша голова уже готова будет взорваться и забрызгать всё вокруг мозгами (я и сам помню это ощущение), – но энергия и импульс должны сохраняться! Так как же могут разные наблюдатели не соглашаться с тем, что они собой представляют?

Тут есть ещё больше магии, которая, кстати, была ещё до Эйнштейна. Поверьте мне, Вселенная – очень, очень хитроумный бухгалтер, и, несмотря на то, что разные наблюдатели не будут соглашаться по поводу энергии, имеющейся у объекта или системы объектов, они все согласятся, что эта энергия не меняется со временем. То же касается и импульса.

А вот масса очень сильно отличается от энергии и импульса. Во-первых, масса не сохраняется. В природе есть множество процессов, изменяющих общую массу системы: к примеру, массивная частица Хиггса может распадаться на два безмассовых фотона. С массой не связана симметрия, и поэтому у Нётер нет для нас закона сохранения. Во-вторых, в отличие от энергии и импульса, чьи величины зависят от наблюдателя (в частности, от его скорости по отношению к измеряемым объектам), все наблюдатели согласятся с величиной массы m объекта. А это вовсе не очевидно, и происходит так оттого, как ужасно хитроумно работают уравнения Эйнштейна.

Видео:Импульс тела и импульс силы. Закон сохранения импульса. 10 класс.Скачать

Итак, что мы имеем

На текущий момент у нас несколько, на первый взгляд, противоречивых знаний. Мы знаем, что:

• Энергия и импульс изолированной физической системы сохраняются (общая энергия и общий импульс изолированной системы не меняются со временем) с точки зрения любого наблюдателя.
• Разные наблюдатели, движущиеся относительно друг друга, по-разному оценят величины энергии и импульса системы!
• Сумма масс объектов, составляющих систему, не сохраняется, она может меняться.
• Но все наблюдатели согласятся с величиной массы объекта.

К этому списку нужно добавить ещё два факта и два вывода:

Масса физической системы объектов не равна сумме масс объектов, составляющих эту систему.

Вместо этого масса физической системы, по поводу которой согласятся все наблюдатели, определяется её энергией и импульсом, и удовлетворяет своему варианту уравнения №1:

Получается, что дополнительный закон сохранения не нужен, и что хотя сумма масс объектов, составляющих систему, не сохраняется, масса системы сохраняется, поскольку она связана через уравнение №1′ с энергией и импульсом системы, которые сохраняются.

Масса системы объектов – это единственный пункт нашего списка, одновременно и сохраняющийся, и не являющийся предметом споров наблюдателей.

Нужно лишь помнить, что масса системы объектов – это не сумма масс объектов, составляющих систему, а то, что задано уравнением №1′.

Чем пытаться объяснить это, просто посмотрим, как это работает. Яркий пример стоит тысячи слов. Давайте в качестве примера системы рассмотрим самую модную штуку, а именно, частицу Хиггса (обладающую массой в 126 ГэВ/с 2 ), и посмотрим, как различные утверждения, сделанные выше, работают при её распаде на два фотона.

Видео:Закон сохранения и превращения энергии. 9 класс.Скачать

Одна частица Хиггса, два фотона и три наблюдателя

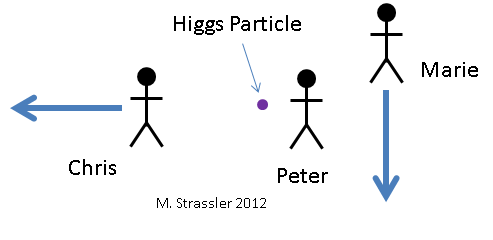
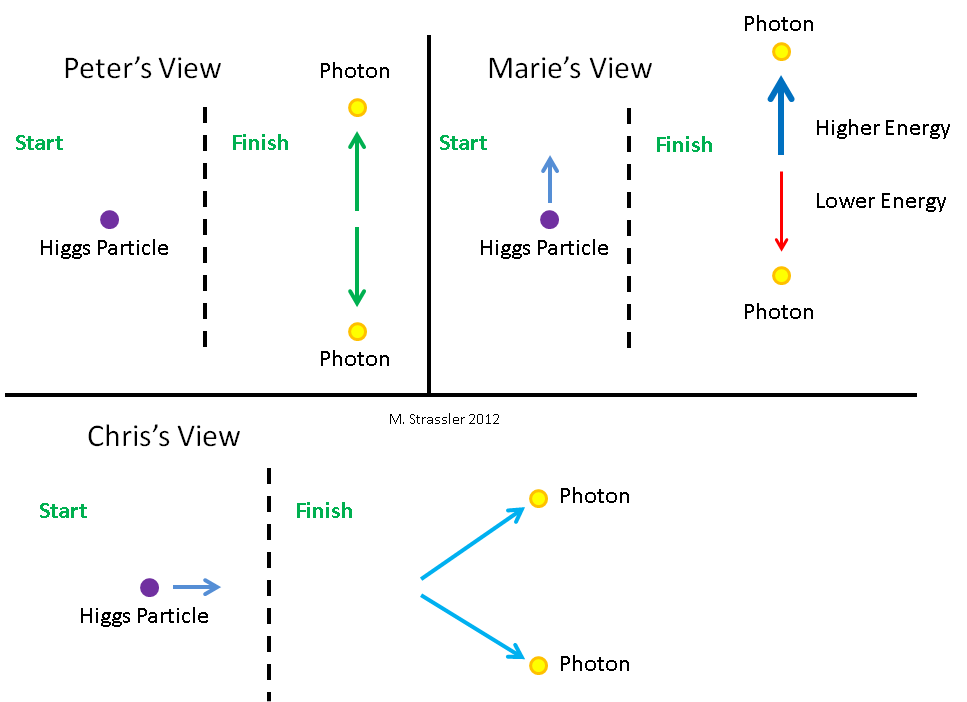
Рис. 6. Три наблюдателя смотрят на частицу Хиггса. По отношению к ней Петя (Peter) не двигается, Маша (Marie) двигается вниз, а Костя (Chris) двигается влево.

Давайте посмотрим на то, как частица Хиггса распадается на два фотона, с точки зрения трёх разных наблюдателей. Они изображены на рис. 6 вместе с частицей Хиггса, на которую они смотрят. Конечно, они не могут увидеть её глазами, ибо она существует слишком малый отрезок времени и она слишком мала. Им необходимо использовать какое-либо научное оборудование. Для Пети частица Хиггса не двигается. Маша двигается вниз относительно Пети. Костя двигается влево относительно Пети. Значит, для Маши частица Хиггса двигается вверх, а для Кости – вправо. Три наблюдателя видят, как частица распадается согласно рис. 7. Петя видит, что Хиггс распадается на два фотона одинаковых энергий, один из которых двигается вверх, а другой – вниз. Маша видит, что Хиггс распадается на два фотона различных энергий, и у двигающегося вверх энергии больше, чем у двигающегося вниз. Костя видит, как Хиггс распадается на два фотона, направляющихся вправо вверх и вправо вниз. Давайте посчитаем, какие энергии и импульсы присвоят Хиггсу и двум фотонам наблюдатели, и как каждый из них придёт к выводу о сохранении энергии и импульса в процессе распада.

Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Распад неподвижной частицы Хиггса

Для начала разберём частицу Хиггса с точки зрения Пети. Петя смотрит (при помощи измерительных приборов) на частицу Хиггса, и что же он видит? (Я буду ставить чёрточку над всем, что видит Петя, и потом мы сравним это с наблюдениями Маши и Кости). Хиггс не двигается, значит, его импульс равен нулю, и согласно уравнению №1 у него, с его массой m = 126 ГэВ/c 2 энергия будет

Теперь, согласно сохранению энергии и импульса, система, состоящая из частицы Хиггса, сохранит всю энергию и импульс после распада. И это будет так, пока никакая внешняя сила не будет воздействовать на Хиггса. Вы можете спросить, нужно ли нам волноваться по поводу земного притяжения, ведь гравитация и будет внешним воздействием, способным менять импульс. Отвечу, что за то краткое время, которое нужно Хиггсу на распад, влияние гравитации будет столько малым, что если бы я рассказал вам, какое оно на самом деле мелкое, вы бы захихикали. Забудьте об этом.

Итак, когда Хиггс распадается, энергии частиц, составляющих его остатки, должны в сумме дать 126 ГэВ, а импульс частиц (учитывая, что импульс – это не только величина, но и направление — вектор) в сумме даст ноль.

Два безмассовых фотона, на которые распадается Хиггс, могут разлететься в любых направлениях, но чтобы упростить пример, представим, что они разлетятся вертикально – один вверх, а другой, отскочив от него, вниз. (Чуть позже обсудим, почему они должны разлетаться в противоположных направлениях).

Каким импульсом обладают фотоны? Это просто. Во-первых, общий импульс системы – сумма импульсов двух фотонов – должен быть нулевым, поскольку у Хиггса до распада был нулевой импульс (с точки зрения Пети). Теперь у каждого из фотонов есть импульс определённой величины и направления. В сумме они могут давать ноль только одним способом – если они равной величины и противоположного направления. Если один идёт вверх, другой должен идти вниз, и величина их должна быть одинаковой.

Рис. 8: что видит Петя

Во-вторых, общая энергия системы – это сумма энергий двух фотонов. Это происходит потому, что между ними нет никакой энергии взаимодействия (кроме крайне малого гравитационного притяжения, о котором можно забыть). Конечно, раз у них нет масс, то вся их энергия заключается в энергии движения. Кроме того, в случае для безмассовой частицы уравнение №1 говорит о том, что E = p c, где p – величина импульса. Из-за этого два фотона с одинаковыми импульсами должны обладать и одинаковыми энергиями. А поскольку две эти энергии в сумме должны дать энергию частицы Хиггса, то энергия каждого фотона должна равняться половине энергии частицы Хиггса.

А поскольку для безмассовой частицы p = E/c, то

И это отображено на рис. 8.

Энергия и импульс сохраняются, а масса – нет, поскольку у фотонов нет массы, а у Хиггса была. А что по поводу массы системы? Какова масса системы из двух фотонов? Ненулевая. Очевидно, какая она. Точно так же, как и для самого Хиггса (из которого и состояла изначально вся система), система из двух фотонов обладает той же энергией и импульсом, что были у Хиггса:

А поскольку для Пети ,

Что и есть масса Хиггса. Масса системы не изменилась за время распада, как и ожидалось.

Видео:Урок 109. Момент импульса. Закон сохранения момента импульсаСкачать

Наблюдатель, для которого Хиггс движется вверх

Маша движется вниз по отношению к Пете, так что с её точки зрения Петя и Хиггс двигаются вверх. Допустим, что Хиггс двигается со скоростью v = 0,8 c, то есть 4/5 скорости света, относительно неё. В отличие от Пети, с точки зрения Маши Хиггс обладает ненулевым импульсом, а импульсы у фотонов оказываются разными по величине, но по-прежнему разнонаправленными – в результате чего сумма их импульсов будет ненулевой.

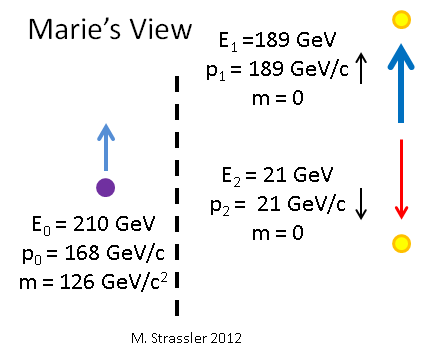
Рис. 9: как Маша видит распад частицы Хиггса

Как посчитать, какими импульсом и энергией обладает Хиггса и два фотона, на которые он распадается, с точки зрения Маши? Для этого нам понадобится ещё один набор простых уравнений Эйнштейна. Допустим, с точки зрения некоего наблюдателя объект обладает импульсом p и энергией E. Тогда с точки зрения другого наблюдателя, движущегося со скоростью v по направлению движения объекта (или против него), импульс и энергия объекта будут выражаться следующим образом:

Где γ удовлетворяет ещё одному пифагорову уравнению:

согласно Эйнштейну. Это позволяет нам выполнять преобразования между тем, что видит Петя, и тем, что видит Маша (или любой другой наблюдатель, двигающийся со скоростью v). То, что мы обнаружим, показано на рис. 9.

Чтобы сравнить наблюдения Маши с наблюдениями Пети, нам понадобятся v и γ. Я утверждаю, что если v=4/5 c, то γ = 5/3.

Проверим, используя уравнение №5: 1 = (4/5)2 + (3/5)2 = 16/25 + 9/25 = 25/25

Петя говорит, что у Хиггса . Что насчёт Маши? Она говорит, что:

Петя утверждает, что у двух фотонов , и для каждого из них E = p c. Теперь мы можем подсчитать, что видит Маша, используя уравнения №4 и №4.

Работает! Энергия сохраняется и с точки зрения Марии, ибо

Импульс тоже сохраняется:

Масса системы совпадает с массой Хиггса до и после распада, поскольку до и после распада

Что, согласно уравнению №1′, приводит массу системы вновь к , как и у Пети, поскольку

Видео:Применение закона сохранения и превращения механической энергии. Практическая часть. 9 класс.Скачать

Наблюдатель, с точки зрения которого Хиггс движется вправо

Что у нас с Костей? Костя двигается влево относительно Пети, допустим, со скоростью v=4/5 c, так что относительно Кости Хиггс (и Петя) двигаются вправо со скоростью v=4/5 c. Те же расчёты, что мы делали для Маши, показывают, что энергия Хиггса , но, в отличие от Маши, для которой Хиггс двигается вверх, для Кости импульс Хиггса направлен вправо. Это изображено на рис. 10.

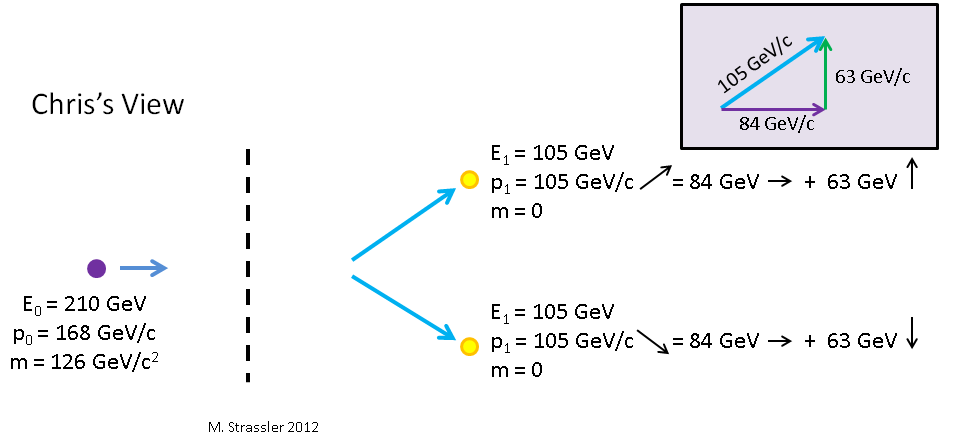
Рис. 10

Хиггс распадается на два фотона. Если с точки зрения Пети фотоны двигаются вверх и вниз, то для Кости, наблюдающего, как Хиггс и Петя двигаются вправо, один из фотонов двигается вправо вверх, а другой – вправо вниз. Какие у них тогда будут импульс и энергия?

Через уравнения №4 и №5 нам этого не узнать, поскольку они предназначаются для случаев, когда частица и наблюдатель двигаются в одном направлении. Для нашего случая уравнения будут такими:

Эти уравнения будут проще, чем кажутся, поскольку с точки зрения Пети, у p нет компоненты, двигающейся слева направо, и весь импульс идёт вверх или вниз. Так что Костя наблюдает следующие величины для Хиггса:

А у фотона, идущего вверх

Для второго фотона формулы те же, только его вертикальная составляющая направлена вниз. Заметьте, что для обоих фотонов E = p c, согласно теореме Пифагора для размера p у каждого из импульсов – согласно врезке на рис. 10

И вновь Костя наблюдает другие величины энергии и импульса, по сравнению с Петей и Машей. Но и для Кости энергия и импульс всё равно сохраняются. Также Костя наблюдает, что у системы с двумя фотонами масса совпадает с массой Хиггса. Почему? Общая вертикальная часть импульса системы нулевая, она взаимно уничтожается. Горизонтальная часть импульса системы равна 168 ГэВ/с. Общая энергия системы 210 ГэВ. Это то же, что наблюдала Маша, за исключением того, что у неё импульс системы шёл вверх, а не вправо. Но направление импульса не влияет на уравнение №1′. Там играет роль только его величина. Так что, как и Маша, Костя видит, что масса системы из двух протонов получается , равной массе первичной частицы Хиггса.

Итак, мы видим, что наблюдают три разных наблюдателя. Их наблюдения:

• разнятся по поводу того, какие у Хиггса энергия и импульс,
• разнятся в части энергии и импульса обоих фотонов,
• согласуются по поводу сохранения энергии и импульса при распаде,
• следовательно, они согласны, что при этом сохраняется масса системы,
• соглашаются, что масса системы равна 126 ГэВ/c 2 ,
• и более того, что сумма масс объектов системы не сохраняется, а уменьшается с 126 ГэВ/c 2 до нуля.

И это не случайно. Эйнштейн из предыдущих экспериментов знал, что энергия и импульс сохраняются, поэтому он искал и нашёл уравнения, сохраняющие эту особенность мира. Также в процессе он обнаружил, что масса системы должна удовлетворять уравнению №1′.

Видео:Закон сохранения энергии. 9 класс. Решение задачСкачать

Бонус: как это используется в поисках частицы Хиггса

• наблюдают столкновения протонов, в результате которых рождается два фотона;
• подсчитывают массу системы из двух фотонов (на техническом жаргоне это называется инвариантная масса пары фотонов).

Когда в результате эксперимента получается частица Хиггса, распадающаяся на два фотона, то вне зависимости от того, в каком направлении и с какой скоростью двигается частица по отношению к лаборатории, система из двух фотонов, на которую она распадётся, всегда будет обладать массой, равной массе частицы Хиггса, произведшей их на свет! Поэтому, в отличие от случайных процессов, в результате которых получается система из двух фотонов случайной массы, частицы Хиггса всегда будут порождать систему из двух фотонов одной и той же массы. Поэтому, если в результатах эксперимента появятся частицы Хиггса, и если они иногда будут распадаться на два фотона, то мы увидим пик от распадов Хиггса, возвышающийся над гладким фоном из других случайных процессов. Так и произошло в эксперименте на БАК!

Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Баланс количества движения

Далее эта величина складывается из суммарного потока импульса через всю управляющую поверхность и скорости изменения суммарного количества импульса в управляющем объеме(напомним, что управляющий объем является стационарным). (5.2)） В этом уравнении, например, DA-это поток жидкости через участок (1A (м3 / с)), а значения rih можно рассматривать как плотность x-компонента импульса (momentum) (kg-m / s) 1m.

Сила Gx создает результирующий Gxr, направленный на противоположную сторону оси x, поскольку давление увеличивается в положительном направлении оси X. Секс; технологию wcn » ЦЖР «GuBdСи ^ ТХ ^ 0Л’», » онлайн Х Тело (пример нано, стенка трубы) n может быть твердым в частях, действующих на внешние силы. * ’Пример-если ранг Kx имеет полностью определенную P3 «Ятваемую трубу», слейте ее. Здесь мы перепишем уравнение A и M°LN° «изменение объемной подынтегральной функции/ n-2 этих сил и величины движения (обозначенной rez)» BB0. Res * * «массовый» вывод- // е » Хи soveil = Формула (5. 3) при применении к сегменту m он ориентирован вдоль оси x, как показано на рисунке.

3. П2, Эл= -, потому что а =±1,0, поэтому (5.3） * «Х3?Матчи УУТРУБЫ ’005К0Т0Р0Р ° лллл ° лллл°». Здесь. (5.4） («X) yer Uy’L. а в случае стационарного уравнения (5. 4) быть、 1-я(Фер = д г _ п х г * ху) » «a08 ggV» ^ xh:^ m; wnp: p / = » и a2 скорость не изменяется、 (5.5)） (5.6)в уравнении состояния текучей среды она становится силой. Уравнение площади (5. 4) если он становится+(5.7) «»Си.«для n, кривой оси должны быть использованы, и импульс должен быть использован.

Уравнение баланса для компонента y (5.8).） Пример(5. 3) в вопросе рассматривается труба с изогнутой осью. Конечно, в более общих случаях следует также рассмотреть уравнение баланса компонента R с числом точек на дюйм> Если труба не горизонтальна, то соответствующая составляющая силы тяжести должна быть включена в правую часть формулы баланса количества. При изучении и проектировании роторной машины действия, такой как турбина или роторный „насос“, уравнение равновесия импульса через крутящий момент и момент k0 „„CESa ““ K0 Такие проблемы не учитываются в других книгах, например Хунзакер и Райтмаир [69]П?

ИВОД1 х помогает решать уравнения пограничного слоя и уравнения движения, когда они учитываются позже, наряду с прямым применением уравнений равновесия импульса, которые показаны в задаче. Вода при расходе 568 л / мин проходит через горизонтальное сопло, точнее, перепад давления dr. Do вы делаете это, когда пирог Пирог? (4. 21), игнорируя трение. Шляпы-Ар д 2 е (1） В зависимости от условий, скорость сечения сопла не изменяется на новый расход. УР = −56 ^ — = 9.47 кг / с За задание Рассчитайте скорость： IV 9.47-4-10 * _o. o7 м / с： «В1 = ^ 7Т〜1000-3.14-7.62」 hb = 2,07-(3/1) = 18,6 м / с.

Из формулы (1) д-р.= _ 08.6） »-（2.07）。 1000 = _1171.10, Ф / w2_175kg / см、 Для определения BX используйте формулу баланса импульса (5. 6) Использование. Аих + Рхр-ВХ. (2） Для решения этой задачи в уравнении баланса импульса сопло 11 °volvolume должно содержать стенку= L! Сила, направленная на фигуру. 5.1 Влрав? И упражнения А2-левая сила p2A2.In кроме того, » асферическое давление во внешней части сопласоздает результирующее давление^равное левому направлению в 1 направлении. Поэтому синтетическая сила giaдиаметр МШ1ЫШШ (рис.6), механическая энергия прпнп? Сходятся к образованию вихря. Постепенно меняется р * р-PaA2 4-па (ЛК-Л2) — PxLx = а, (ПВ-ПВ). Теперь подставим номер выражения (2).

Д8 = 157-777 = −620 Н = −63.4 кг. »*0 ° с Лку Резульпрую1чая сила НХ, приложенная к соплу, отрицательная топишая ось Яо » ₽ » авлгпакс и ток противоположный. Приманка закреплена на входе, поэтому ее стенки растянуты. Пример 5.2 — Лу? А * внезапно расширяется, когда жидкость выходит из жидкости»?Эль’g.1?Л?1diamZR (рисунок 5-2), такие как сопло примера 5, механическая энергия поперечного сечения 1, потери энергии очень малы.

• Используя уравнение баланса импульса, вы получаете уравнение энергии a, потерянной при внезапном расширении потока несжимаемой жидкости. Рассмотрим простой пример, когда скорость обеих труб постоянна в поперечном сечении. Уравнение.>*((О) это、 I7 с ВХ. C6 = — / ’ объявление. Рисунок 5. 2.Расширение потока. * ! — ! ’ ** 1-1 1 0 −2 −2.» * (1） I «» TR°L, wi c6161 *’, окруженный плоскостями 1 и 2, с колпачком, выбранным таким образом, что YX исчезает. Далее, по предположению, она течет только по поверхности PLA0.Все потери вызваны только конверсией, Px&= 0.Вместо этого используйте Pxp L2 (p2 — px). I7Di6 = — П2(Р2-Р1).

Потому что P1 и Rch постоянны по всему сечению трубы、 Это Предусмотренный Po = P1-используя соотношения h = b0 eA и u6r=, уравнение сводится к следующему виду: / ^ » /является уравнением равновесия механической энергии, примененным к этой задаче、 4CH1-Ш- 1 = 2г- Последние 2 уравнения, желаемый результат будет получен Часто, p ^^ PeE (5°)°^^^потеря потеря — ■- Горизонтально расположенные гладкие Как показано^ D ^.^ О » Рассчитаем величину и направление силы, необходимой для удержания колена(в контрольный объем следует включить стенку трубы.

в этой задаче будем считать, что скорость распределяется равномерно, сначала по оси x, а затем в первом направлении * сечения находим следующее: Ту(ix2-Hx1)= — При — (о Потому что точка 2 не имеет скорости^^ c ^ aw*, а * «- выходит » — равно всем направлениям. Таким образом, общая прочность при = — а(ру-Рау, Ях = — топор(Р1-Ра) -= = 3,14-5,1 «(_14).9> 8_a4L0002l (м) −10±а = 4 = —280—1190-=-1470 n = 150 кг. Полная потеря и———• Pa внезапное расширение, более точное представление^ 1 Пример 5. 3. В 90-х годах вода текла из 1 рта、 Как показано на рисунке К / Рисунок 5. 3.Текущий Труба. Изогнутый (4 )） (5） Вход 1.4 at.

Не обращайте внимания на трение Сиппявление Си- Точно так же、 ПУ = П2 (Р2-РО)+ = 280 + 1190 = 1470 Н = 150 кг Результирующая сила равна p = 45°, ее величина равна Меня проинструктировали. 150 / pop 45° = Обозначено 212 кг. Рисунок 5. 3, косые задачи 5. 1.Вода течет через горизонтальный диффузор, который состоит из секции труб, внутренний диаметр которых постепенно увеличивается от 5 см до 10 см. Если расход составляет 3800 л, рассчитайте результирующую силу, действующую на диффузор! Избыточное давление на выходе минимальное и составляет 4,2 атм. 5. 2. Расход воды, протекающей по горизонтально изогнутой части под углом 50°от 45-литровой трубы, эквивалентен 760л!

Если избыточное давление на выходе составляет 3,5 Ат, вычислите силу, приложенную к колену, и проигнорируйте трение. 5. 3.Несжимаемая жидкость течет вдоль плоской пластины с единичной шириной. Удаляясь от пластины, поток является равномерным и имеет скорость u0 в направлении, параллельном пластине. Жидкость не скользит по пластине, и под действием слоя, ближайшего к пластине, движение вязкой жидкости замедляется по мере приближения к пластине. plate. To Рисунок 5.

Пограничный слой на плоской пластине. В икс 1-пластина; 2-линия потока. Образуется пограничный слой (так называемая область течения, где скорость изменяется от нуля на пластине до скорости падающего однородного потока и^.Пограничный слой начинается на переднем конце пластины и постепенно утолщается вниз по течению. Немного в стороне от края пластины, для толщины слоя b, приближенная формула параллельной пластины компонента скорости равна Используя уравнение равновесия импульса, мы представляем вычисленные силы сопротивления на одной стороне пластины как функцию u0, p и b, предполагая, что давление везде постоянно.

Выберите управляющую поверхность таким образом, чтобы поток через управляющую поверхность протекал только в направлении оси X. Условие задачи проиллюстрировано на схеме. 5. 4.Линия обтекания, показанная здесь, является линией, в которой жидкость не течет. Линия o (x)не является линией потока. 5. 4.Рисунок 5. 5 эжектор предназначен для закачки воздуха в атмосферу из зоны, где давление воды составляет 50 мм. Искусство. Ниже атмосферы. Тело выталкивателя 80 в диаметре. ч.

К стальной трубы, ее сечение значительно больше, чем сечение сопла. Давление нагнетаемого воздуха таково, что на выходе из сопла создается скорость воздуха АОО м / с, близкая к скорости звука. Плотность воздуха практически не изменяется и может быть принята постоянной на уровне 1,2 кг! Кубометр. Напишите формулу для импульсного баланса объема между секциями 1 и 2, и вы увидите соотношение расхода нагнетаемого и уносимого воздуха(1Р и IVe).в секции 2 поток хорошо перемешан и скорость постоянна по поперечному сечению, как это было непосредственно перед секцией 1.Сопротивление Pxl можно игнорировать. Также рассчитываются максимальный расход уносимого воздуха и соответствующий размер сопла. 5.

Ламинарные профили скорости потока представляют собой полностью развитые потоки несжимаемой жидкости, которые внезапно расширяются при переходе к трубам большего диаметра, и скорость равномерно распределяется по поперечному сечению. Способ вывода Я Но… Два Рисунок 5. 5.Функция выталкивателя. а-нагнетаемый воздух; Б-увлекаемый воздух; Р = 50 мм воды. Искусство. (Вакуум.) L-пример отношения 5. Это было сделано в 2 часа. При рассмотрении этой проблемы иногда используют формулу (80]. Покажи мне. (1） Ш-1ш- (2） Это выражение ^не только потерянная энергия、 В ламинарном движении формула кинетической энергии-y неверна. *Эта статья рассчитает потери давления за короткое время нагрева exchanger.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Физика 10 класс (Урок№11 - Импульс. Закон сохранения импульса.)Скачать

Сплошная среда (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

Таким образом, изменение внутренней энергии макро частицы работой внешних сил равно

Деформации меняют расстояния между частицами внутри макро частицы и тем самым меняют их энергию взаимодействия.

Суммируя сказанное, изменение внутренней энергии макро частицы можно записать в виде

Деля обе части равенства на Δm — массу макро частицы и обозначая массовую плотность внутренней энергии как e ≡ ΔEint/Δm, запишем

Как, зная внутреннюю энергию, получить уравнения термодинамического состояния?

Из (3.1’’) следует, что

Итак, если известна функция e = e(s,uik), то могут быть найдены соотношения (3.2), которые и являются уравнениями термодинамического состояния вещества (см. также , , «Статистическая физика», часть 1, §§ 12-15).

Например, если в изотропном веществе отсутствуют касательные напряже­ния и тем самым σik = —pδik, то

В этом случае d(ΔE) = Td(ΔS) – pd(ΔV), а для единицы массы среды имеем

Соответствующие уравнения термодинамического состояния принимают вид

Другие термодинамические потенциалы

Кроме внутренней энергии в термодинамике есть другие термодинамические потенциалы.

Выражение (3.1’) для дифференциала внутренней энергии макро частицы можно переписать в виде

Для этого, как видно, достаточно вычесть из обеих частей полный дифференциал произведения температуры на энтропию. В правой части полученного выражения стоит дифференциал функции, где независимыми переменными является температура T и тензор деформации uij. Эта функция ΔF(T, uij), которую называют свободной энергией Гельмгольца (или, кратко, свободной энергией), связана с внутренней энергией простым соотношением

Разделив обе части выражения для дифференциала свободной энергии на массу макро частицы Δm и обозначив f = ΔF/Δm , получим

Отсюда следует, что если в качестве термодинамического потенциала задана свободная энергия как функция температуры и деформаций, то уравнения термодинамического состояния вещества могут быть получены из соотношений

В частности, для изотропной среды, в которой отсутствуют касательные напряжения и где, следовательно, тензор напряжений имеет вид шарового тензора σij = — p δij

Еще один термодинамический потенциал ΔW, так называемая энтальпия, или тепловая функция, зависит от энтропии и напряжений в среде. В случае изотропной среды и при отсутствии касательных напряжений дифференциал массовой плотности энтальпии w получается из дифференциала внутренней энергии (3.1’’’) добавлением полного дифференциала отношения давления к плотности

Отсюда также можно записать уравнения термодинамического состояния в форме

Зная любой термодинамический потенциал, можно получить уравнение термодинамического состояния.

Например, статистическая физика в случае идеального газа при­водит к следующему выражению для свободной энергии макро частицы

где f(T) — некоторая функция температуры.

Отсюда уравнения термодинамического состояния имеют вид

Последнее соотношение есть упомянутое выше уравнение Клайперона.

Итак, уравнения термодинамического состояния, которые в механике сплошной среды предполагаются заданными, связывают между собой термодинамические параметры вещества в каждой точке вещества и в каждый момент времени независимо.

Уравнение непрерывности массы

Термодинамические параметры в общем случае могут зави­сеть от того, где находится макро частица, и момента времени (нестационарный процесс). Эти зависимости обусловлены вза­имодействием макро частиц между собой и их перемещением. Взаимодействие макро частиц приводит к изменению их внутренних энергий и аргументов внутренней энергии — термодинамических параметров ΔV (или, в общем случае, uik) и ΔS.

Согласно резуль­татам первого раздела имеет место соотношение

Деля числитель и знаменатель левой части на Δm и учитывая, что масса макро частицы постоянна, получим

(3.3)

Уравнение (3.3) называется уравнением непрерывности. Оно содержит две полевые функции ρ(r,t) и v(r,t) и является уравнением в частных производных.

Уравнение непрерывности можно записать в другой форме, если выразить полную производную dρ/dt через частные производные .

Учитывая, что , получим уравнение непрерывности в виде:

(3.4)

Если вещество можно считать несжимаемым, то есть d(ΔV) = 0, то уравнение непрерывности имеет вид:

Наконец, если выделить некоторый конечный объем пространства V, заполненный веществом, и проинтегрировать (3.4) по этому объему, то получим

,

(3.6)

Соотношение (3.6) означает, что изменение массы вещества, заключенной в объеме V, в единицу времени равно потоку массы внутрь этого объема через окружающую его поверхность. Знак минус указывает на то, что поток направлен внутрь, то есть против внешней нормали. Величина ρv есть плотность потока массы, то есть масса, протекающая в единицу времени через единицу поверхности; ρvdf — поток массы через элементарную площадку df.

Соотношение (3.6) есть уравнение непрерывности, записанное в интегральной форме.

Уравнение теплопроводности

Теперь рассмотрим уравнение, описывающее динамику изменения энтропии частицы.

Изменение энтропии в единицу времени, умноженное на температуру есть изменение внутренней энергии макро частицы за счет теплового потока внутрь частицы. Поэтому, если q — плотность теплового потока, то .

По теореме Гаусса: .

Учитывая малые размеры макро частицы, имеем

.

Подставляя этот результат в выражение для теплового потока, получим

Деля обе части на ΔV, получим

. (3.7)

Плотность потока тепловой энергии q зависит от разности температур между макро частицей и окружением, то есть от градиента температурного поля ∂T/∂xi. Если этот градиент не очень велик, то функцию q = q(∂T/∂xi) можно разложить в ряд Тейлора вблизи точки ∂T/∂xi = 0, ограничившись первыми неисчезающими членами разложения.

.

При отсутствии градиента температуры тепловой поток не возникнет, поэтому 1-ые неисчезающие члены линейны по ∂T/∂xi. Обозначая коэффициенты при первых производных

, (3.8)

получим — так называемый закон Фурье, установленный экспериментально. Знак минус в этом соотношении подчеркивает тот факт, что вектор плотности теплового потока направлен против градиента температуры.

Подставляя выражение для qi в правую часть (3.7), получим для однородной среды

(3.9)

Тензор , определенный (3.8), называется тензором теплопроводности. В физической кинетике доказывается, что тензор теплопроводности образует положительно определенную симметрическую матрицу. В случае изотропной среды, то есть среды, в которой все направления равноправны, тензор является шаровым и имеет вид , где — коэффициент теплопроводности. В этом случае уравнение (3.9), называемое уравнением теплопроводности, принимает вид , или

(3.10)

Если воспользоваться одним из уравнений термодинамического состояния (3.2) и выразить энтропию s через тензор деформаций uik и температуру T, то уравнение теплопроводности будет содержать три полевых функции — плотность ρ(r,t), температуру T(r,t) и тензор деформаций uik(r,t).

Замкнутая система динамических уравнений

Полученные уравнения — уравнение изменения импульса макро частицы (2.3), уравнение непрерывности (3.3), уравнение теплопроводности (3.9) и уравнения термодинамического (3.2) состояния представляют собой замкнутую систему уравнений для полевых функций ρ, T, v, s, σik, uik, характеризующих динамическое состояние вещества в каждой его точке. Посчитайте число уравнений и неизвестных функций.

Вязкость

Теперь учтем взаимодействие «внешних» степеней свободы макро частицы с «внутренними». Такое взаимодействие переносит энергию с небольшого числа «внешних» степеней свободы на бесконечное число «внутренних», распыляя ее практически безвозвратно. Это явление носит название вязкости, или трения.

В процессе трения внутренняя энергия макро частицы растет за счет относительного движения макро частиц. Другими словами этот рост имеет место лишь в том случае, если отлична от нуля разность скоростей макро частицы и окружающего вещества, а, следовательно, отличен от нуля градиент скорости ∂vi/∂xk в точке, где находится частица. Важен, правда, не весь градиент, а лишь его симметрическая часть. Ведь кососимметрическая часть градиента скорости равна , где χik — тензор бесконечно малых поворотов. Этот тензор определяет вращение макро частицы как абсолютно твердого тела, а не ее движение относительно окружения. Симметрическая часть тензора ∂vi/∂xk есть тензор скоростей деформаций

.

Таким образом, рост внутренней энергии макро частицы в процессе трения должен определяться некоторой функцией тензора скоростей деформаций . Функция называется диссипативной функцией единицы объема вещества. Она определяет диссипацию, то есть необратимое рассеяние энергии «внешних» степеней свободы макро частицы на «внутренних».

Разделив обе части записанного соотношения на массу частицы Δm, получим:

(3.11)

где e — внутренняя энергия массы вещества.

Диссипация энергии «внешних» степеней свободы ощущается как проявление некоторых напряжений, действующих на макро частицу при ее движении в среде, то есть некоторых сил трения. Из (3.11) можно определить тензор напряжений, соответствующий этим силам, — тензор вязких напряжений σ’ik. Для этого надо воспользоваться соотношением (3.1), учтя, что изменение энергии (3.11) определяется работой сил трения и поэтому ds в (3.1) необходимо положить равным нулю, а σik, равным σ’ik. Тогда получим

(3.12)

Соотношение (3.12) и определяет тензор вязких напряжений через диссипативную функцию.

Обычно градиенты скорости частиц сравнительно малы и диссипативную функцию раскладывают в ряд вблизи точки vik = 0, оставляя первые неисчезающие члены разложения. Производя такое разложение, получим:

Нулевой член разложения равен нулю, так как при отсутствии относительного движения частиц диссипация не возникает. Первый член разложения тоже равен нулю, но по иной причине. Дело в том, что поскольку диссипация необратима, то внутренняя энергия может в этом процессе только возрастать. Поэтому согласно (3.11) диссипативная функция может быть только положительна. Но в приближении, линейном по vik, ее знак зависел бы от знака vik.

Следовательно, коэффициенты первого приближения должны равняться нулю. Остается принять, что первым неисчезающим приближением, является 2-ое приближение, имеющее вид квадратичной формы (положительно определенной) тензора скоростей деформации:

(3.13)

Здесь — тензор вязкости.

Тензор вязкости симметричен по перестановкам i ↔ k, l ↔ m ik ↔ lm. Эта симметрия приводит к тому, что в самом общем случае у тензора ηiklm 21 независимая компонента (покажите самостоятельно.)

В простейшем случае изотропной среды компоненты тензора вязкости могут быть выражены всего через две независимые постоянные. Этот факт объясняется тем, что имеется всего два независимых тензора 4-ого ранга, скомбинированных из единичных тензоров и обладающих свойствами симметрии, такими же, как ηiklm. Это δikδlm и δ(ilδkm) = (δilδkm + δimδkl)/2. Поэтому в изотропном случае можно записать тензор вязкости в виде ηiklm = Aδikδlm + Bδ(ilδkm), где A и B – некоторые коэффициенты, характеризующие вязкость в изотропном случае.

Согласно (3.12) и (3.13) тензор вязких напряжений принимает вид

В изотропном случае σ’ik = Aδikvll + Bvik.

Раскладывая в правой части vik на шаровой и девиатор, получим

🌟 Видео

Закон сохранения импульса. Решение задач. 9 классСкачать

Импульс тела. Закон сохранения импульса | Физика 9 класс #20 | ИнфоурокСкачать

Закон Сохранения Энергии // Урок по Физике 7 класс - Закон Сохранения Механической ЭнергииСкачать

Урок 316. Импульс. Работа. Энергия (повторение)Скачать

Физика 9 класс. §20 Закон сохранения импульсаСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Энергия и закон сохранения энергии | Физика ЕГЭ 2023 | УмскулСкачать