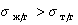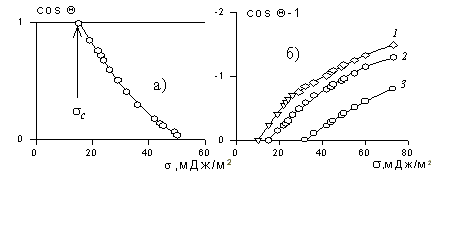Уравнение юнга и явление смачивания

Видео:Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

Поверхностные явления и адсорбция

Кандидат химических наук, доцент

Видео:Урок 199. Смачивание. Капиллярные явленияСкачать

Тема 1. Поверхностные явления и адсорбция

Занятие 2. Поверхностные явления

2. Смачивание и растекание.

3. Основные понятия и характеристики адсорбции.

4. Изотермы и изобары адсорбции

Видео:Смачивание. Капиллярные явления. 10 класс.Скачать

ЛИТЕРАТУРА

1. Фролов коллоидной химии. – М.: Химия, 1989. – С. 25-31, 78-96.

2. Коллоидная химия. – СПб.: «Лань», 2003. – С. 70-76.

Видео:Опыты по физике. Смачивание и краевые углыСкачать

НАГЛЯДНЫЕ ПОСОБИЯ И ПРИЛОЖЕНИЯ

Работа когезии и адгезии

Видео:Поверхностное натяжениеСкачать

Краевой угол смачивания

Критерии смачивания и несмачивания

Видео:4.2. Межмолекулярные и межфазные взаимодействияСкачать

ВВЕДЕНИЕ

Изучение поведения жидкостей на твердых и жидких поверхностях представляет большой интерес в связи с широкой распространенностью явлений смачивания и растекания как в природе, так и в различных отраслях народного хозяйства. Явления смачивания и растекания лежат в основе процессов отмывания жидких загрязнений с твердых покрытий. Начнем с изучения понятий адгезии и когезии.

1. АДГЕЗИЯ И КОГЕЗИЯ

Когезия характеризует взаимное притяжение частиц (атомов, молекул) однородного тела, обусловленное силами межмолекулярного взаимодейст-вия, действующими внутри тела.

Когезия характеризует прочность тел на разрыв. Она сильна в твердых телах, меньше в жидкостях.

Адгезия характеризует взаимное притяжение частиц различных тел в области их соприкосновения (т. е. на поверхности раздела фаз), обусловленное силами межмолекулярного взаимодействия, действующими между этими телами.

Количественно когезия и адгезия характеризуются соответственно работой когезии Wк и работой адгезии Wa. Эти величины измеряются в тех же единицах, что и поверхностное натяжение (Дж/м2, Н/м), и они связаны с поверхностным натяжением (рис. 1).

Работа когезии Wк – работа, которую надо совершить для разрыва однородного тела по сечению с единичной площадью на две части. Эта работа затрачивается на разрыв межмолекулярных связей внутри тела. Представим мысленно цилиндр из какой-либо жидкости с единичной площадью сечения S (рис. 1). Разорвем этот цилиндр на 2 части.

Рис. 1. К выводу соотношения между когезией и

Образовалась новая поверхность площадью 2S на границе жидкость – газ. Если вспомнить физический смысл поверхностного натяжения (это работа, которую надо совершить, чтобы увеличить на единицу площадь поверхности раздела фаз), то можно записать

где Wк – работа когезии, Дж/м2;

sЖ-Г – поверхностное натяжение на границе раздела

жидкость – газ, Дж/м2.

При разрыве твердого тела на две части работа когезии соответственно равна

где sТ-Г – поверхностное натяжение на границе раздела

твердое тело – газ, Дж/м2.

сразу можно отметить, что работа когезии тем больше, чем больше величина поверхностного натяжения.

Работа адгезии Wa – работа, которую надо совершить для разрыва двух соприкасающихся тел с единичной площадью контакта. Эта работа затрачивается на разрыв межмолекулярных связей, возникающих на границе раздела фаз.

Рис. 2. К выводу соотношения между адгезией и

Пусть в соприкосновении находятся две несмешивающиеся жидкости с единичной площадью контакта. Граница раздела фаз характеризуется поверхностным натяжением sЖ1- Ж2. После разрыва исчезла граница раздела фаз ж1-ж2, но появились две новые площади поверхности, которые характеризуются поверхностным натяжением sЖ1- Г и sЖ2 — Г.

Очевидно, что работу адгезии можно рассчитать по формуле

Wa = sЖ1- Г + sЖ2 — Г – sЖ1- Ж2 (3)

Это выражение называется уравнением Дюпре.

По аналогии при отрыве жидкости от твердой поверхности совершается работа адгезии, равная:

Wa = sЖ — Г + sТ — Г – sТ — Ж (4)

По уравнению (3) работу адгезии вычислить достаточно легко, поскольку все входящие в него величины определяются экспериментально.

По уравнению (4) рассчитать Wа практически невозможно, т. к. определение поверхностного натяжения на границе с твердым телом представляет собой сложную экспериментальную задачу.

Силы когезии и адгезии играют большую роль в процессах смачивания и несмачивания жидкостями твердых тел, склеивания материалов, нанесения лакокрасочных и других покрытий, печатания, крашения.

2. СМАЧИВАНИЕ И РАСТЕКАНИЕ

Смачивание – это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом).

При нанесении капли жидкости на поверхность твердого тела (или другой жидкости) можно наблюдать разные явления. В одном случае нанесенная жидкость сохраняет форму капли, в другом случае капля растекается по поверхности. Рассмотрим первый случай (рис. 3)

Рис. 3. Смачивание жидкостью твердого тела

Линия соприкосновения трех фаз называется периметром смачивания. Угол q называется краевым углом смачивания. Он отсчитывается со стороны жидкости. Поскольку капля находится в состоянии равновесия, действие сил на нее скомпенсировано. Рассмотрим эти силы. Как известно, силы поверхностного натяжения направлены на сокращение площади контакта фаз и действуют по касательной к поверхности. На рис. 3 эти силы представлены векторами, выходящими из точки соприкосновения всех трех фаз.

sТ-Г – стремиться уменьшить площадь контакта твердого тела с газом, поэтому растягивает пленку жидкости по твердому телу.

sТ-Ж – стремится уменьшить площадь контакта твердого тела с жидкостью, поэтому стягивает каплю жидкости в шарик.

sЖ-Г – стремится уменьшить площадь контакта жидкости с газом, поэтому стягивает каплю жидкости в шарик (шарообразная поверхность имеет наименьшую площадь).

Рассмотрим равнодействующую сил, действующих на каплю в точке О вдоль поверхности твердого тела. Эти силы поверхностного натяжения sТ-Г, sТ-Ж, а также проекция sЖ-Г на выбранную ось = sЖ-Г. cosq.

В состоянии равновесия равнодействующая сил равна 0:

sТ-Г = sТ-Ж + sЖ-Г. cosq (5)

Полученное соотношение (5) называется законом Юнга.

Краевой угол смачивания q или cosq являются количественной характеристикой смачивания. Чем меньше угол q и соответственно больше cosq, тем лучше смачивается поверхность.

Закон Юнга позволяет выразить cosq через поверхностные межфазные натяжения:

(6)

Сочетание уравнения Дюпре (4) с законом Юнга (5) позволяет выразить работу адгезии Wa через косинус краевого угла смачивания q.

Из уравнения (5) выразим разность

sТ-Г – sТ-Ж = sЖ-Г. cosq

Полученную разность подставим в уравнение 4

Wa = sЖ-Г + sЖ-Г. cosq = sЖ-Г(1 + cosq) (7)

Уравнение (7) называют уравнением Дюпре – Юнга. Оно позволяет рассчитать работу адгезии, если известно поверхностное натяжение жидкости и краевой угол смачивания. Обе эти величины сравнительно легко определяются экспериментально: q определяют путем проектирования капли на экран (с помощью несложной установки) и измерения краевого угла на проекции капли. С помощью уравнения Дюпре – Юнга (7) легко найти соотношение между работой когезии смачивающей жидкости и работой адгезии между жидкостью и смачиваемым телом.

Краевой угол смачивания (или косинус краевого угла) является характеристикой способности жидкости смачивать твердую или жидкую поверхность. В таблице 1 представлены возможные случаи поведения жидкости на твердой или жидкой поверхности. Смачивание или несмачивание зависит от соотношения работы когезии и работы адгезии.

Таблица 1. Критерии смачивания, несмачивания и растекания

q > 900 (тупой угол)

Смачивание жидкостью поверхности

Капиллярное поднятие или опускание жидкостей связано с возникновением кривизны поверхности (выпуклый или вогнутый мениск). В свою очередь появление кривизны поверхности связано с процессами смачивания (q 900, выпуклый мениск) жидкостями стенок капилляров.

Растекание жидкостей по поверхности

Особо остановимся на предельном случае смачивания – растекании жидкости по поверхности, которое наблюдается при q = 00, когда работа адгезии равна работе когезии (Wa = Wк). Очевидно, что чем больше преобладает работа адгезии над работой когезии, тем лучше будет растекаться жидкость по поверхности. Величина

называется коэффициентом растекания или критерием Гаркинса.

Если f > 0 – жидкость растекается (Wa > Wк)

Изотермы полимолекулярной адсорбции (рис.7) характерны для адсорбции газов и паров на твердых адсорбентах. Изотерма вида а (s-образная изотерма) при невысоких давлениях напоминает изотерму мономолекулярной адсорбции (участок Р1), т. е. на поверхности образуется один слой молекул адсорбтива. При дальнейшем увеличении давление газа на первый слой может сесть второй, третий и т. д. слой молекул, происходит полимолекулярная адсорбция, поэтому адсорбция резко возрастает.

Первый слой молекул удерживается на адсорбенте силами взаимодействия адсорбент — адсорбтив, а второй, третий слои удерживаются силами притяжения между молекулами адсорбтива. Концентрирование адсорбтива на поверхности приводит к тому, что газ (пар) конденсируется и образуется жидкий слой конденсата на поверхности адсорбента.

Рис.7. Изотермы полимолекулярной адсорбции

Рs – давление насыщенного пара

Изотермы адсорбции с капиллярной конденсацией (рис.8) характерны для газов (паров), адсорбирующихся на пористых адсорбентах. Эти изотермы сходны с изотермами полимолекулярной адсорбции, но имеют и некоторые отличия. Пористые адсорбенты имеют многочисленные поры, которые представляют из себя капилляры. При образовании полимолекулярного слоя на стенках пор возникает искривленная (вогнутая) поверхность раздела фаз жидкость – пар, давление насыщенного пара над которой меньше, чем над плоской поверхностью. Поэтому в пористых материалах пар конденсируется при более низких давлениях и конденсация идет до заполнения всех пор. Этот процесс заканчивается раньше, чем достигается давление насыщенного пара. Поэтому изотерма адсорбции выходит на предельное значение (все поры заполнены, адсорбция не идет).

Рис.8. Изотермы полимолекулярной адсорбции,

осложненной капиллярной конденсацией

Рs – давление насыщенного пара

Изобары и изопикны адсорбции

Изобарой адсорбции называется зависимость величины адсорбции газа (или пара) на твердом адсорбенте от температуры при постоянном парциальном давлении газа (пара) А = fр(Т)

Изопикной адсорбции называется зависимость величины адсорбции растворенного вещества от температуры при постоянной концентрации растворенного вещества А = fc(Т)

Процесс адсорбции экзотермичен и, следовательно, в соответствии с принципом Ле-Шателье с ростом температуры величина физической адсорбции уменьшается (рис.9). При повышении температуры колебания адсорбированных поверхностью частиц усиливаются, они отрываются от поверхности, равновесие сдвигается в сторону процесса десорбции.

Рис.9. Изобара (Р = const) или изопикна (С = const) адсорбции.

Описание взаимодействия молекул адсорбтива и молекул адсорбента представляет собой весьма сложную и до сих пор до конца неразрешенную задачу. Рассмотрению некоторых теорий адсорбции будет посвящена следующая лекция.

Сегодня мы познакомились с основными видами поверхностных явлений: смачиванием, растеканием и адсорбцией. Следующая лекция будет посвящена подробному рассмотрению явлений адсорбции, которые играют значительную роль в природе, технологических процессах.

Видео:Капиллярный эффектСкачать

2.3.2. Смачивание и растекание на границе твердое тело – жидкость – газ

В большинстве случаев жидкость на поверхности твердого тела остается в виде капли, большей или меньшей толщины, контактирующей с твердым телом под определенным углом, который называется краевым углом смачивания и обозначается буквой Q (рис. 1.24). Растекание капли по поверхности прекратится при достижении равновесия, которое без учета сил тяжести может быть описано уравнением Юнга:

(1.2.44)

, (1.2.45)

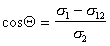
где индексы 1, 2, 3 – обозначают, соответственно, твердую, жидкую и газовую фазы.

Работа адгезии выражается уравнением Дюпре:

(1.2.46)

. (1.2.47)

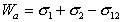
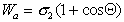
Рис. 1.24. Капля жидкости на поверхности твердого тела (схема)

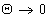
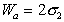
Работа адгезии при ,т.е. при полном смачивании, , что эквивалентно работе когезии жидкости. Если Q = 180 o , соs Q = -1 и в соответствии с уравнением (1.2.47) W_a = 0, т.е. жидкость не смачивает твердую поверхность. При Q» 90 o жидкость проявляет слабое смачивание.

Следует помнить, что определение работы адгезии в реальных системах предполагает равновесие фаз, насыщенных относительно друг друга.

Кроме того, твердая поверхность, по которой происходит растекание жидкости, не свободна. Она обычно покрыта пленкой вещества, адсорбированного из газо-паровой фазы. Эта пленка имеет поверхностное давление p, поэтому

, (1.2.48)

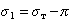
Смачивание неоднородных, пористых или шероховатых поверхностей сопровождается запиранием пузырьков воздуха в неровностях. В результате этого краевые углы смачивания сухой и предварительно увлажненной поверхностей различаются. Такое явление носит название «гистерезис смачивания». Гистерезис смачивания проявляется также при загрязнении поверхности, в результате чего она становится неоднородной при закреплении на ней твердых частиц или жировых пленок. В этом случае поверхность ведет себя как составная.

Шероховатость поверхности учитывается введением коэффициента шероховатости r, представляющего отношение площади поверхности реального тела к площади идеально гладкой поверхности, тогда

. (1.2.49)

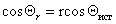
Можно отметить, что если краевой угол смачивания гладкой поверхности, например полимерной пленки, меньше 90 o , то шероховатость (ткань из волокон этого полимера) уменьшает его, если же он больше 90 o , то шероховатость его увеличивает. Для составной поверхности, которая специфична для большинства текстильных материалов, наличие участков различной природы может быть учтено введением коэффициентов x, характеризующих долю поверхности с различными свойствами. Например, если текстильный материал изготовлен из волокон двух видов 1 и 2, то

. (1.2.50)

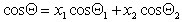
Если переплетение нитей таково, что получается сетчатый или дырчатый материал, то уравнение (2.50) принимает вид

, (1.2.50′)

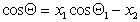
где х₂ – доля открытой поверхности.

Как мы обсуждали выше, поверхностное натяжение можно разделить на компоненты дисперсионных и полярных сил, а при нахождении межфазового натяжения для многих жидких границ можно ограничиться лишь дисперсионной составляющей. Такое ограничение позволяет провести обсуждение явления смачивания (по крайней мере, низкоэнергетических поверхностей, к каковым можно отнести подавляющее большинство волокнообразующих полимеров), в рамках теории дисперсионных сил.

Как показал Н. В. Чураев смачивание неполярной жидкостью твердой поверхности возможно, если будет соблюдаться условие смачивания, которое выражается уравнением

, (1.2.51)

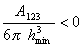
где А₁₂₃ – составная постоянная Гамакера при взаимодействии жидкости (фаза 2) с твердым телом (фаза 1) на границе с воздухом (фаза 3); h_min — наименьшая толщина пленки, которая фактически соответствует Ван-дер-Ваальсову расстоянию, т.е. h_min = (0,22¸0,24) нм. Например, для воды на поверхности тефлона А₁₂₃ = -7·10 — 21 Дж.

Учет только дисперсионных сил приводит к уравнению

, (1.2.52)

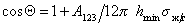
При расчетах углов смачивания твердых поверхностей следует учитывать поверхностное давление пленки, образованной при адсорбции из газо-паровой фазы. Тогда с учетом уравнения (1.2.48), уравнение Юнга (1.2.45) следует записать в виде

. (1.2.53)

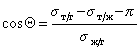
Способ расчета поверхностного давления предложили Бэнгхэм и Разорук:

, (1.2.54)

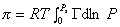
где P – равновесное давление, Г– равновесная адсорбция газа (пара), P_s – давление насыщения.

При больших углах смачивания и слабом взаимодействии жидкости с твердым телом поверхностное давление обычно не учитывают.

Для неполярных жидкостей на низкоэнергетической поверхности твердого тела для работы адгезии было получено выражение

. (1.2.55)

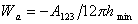
Поэтому уравнение Дюпре (1.2.46) можно записать

. (1.2.55′)

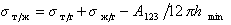
Для дисперсионной составляющей жидкости

, (1.2.56)

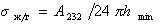
где А₂₃₂ – постоянная Гамакера взаимодействия жидкости через прослойку газа (пара).

Сочетая уравнения (1.2.47), (1.2.55) и (1.2.56), получаем

. (1.2.57)

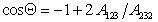
Очевидно, что Q = 0, т.е. при полном смачивании, cosQ = 1, если

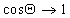
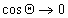
Уравнение (1.2.57) позволяет прогнозировать вероятность смачивания () или наоборот — несмачивания () жидкостью поверхности твердого тела по известным постоянным межмолекулярных сил взаимодействия.

Чаще, однако, прибегают к определению постоянной Гамакера по известному значению межфазового натяжения на границе «твердое тело — газ». Эту характеристику поверхности твердого тела находят при распространении подхода Джирифалько и Гуда, рассмотренного нами выше для границы двух жидкостей, на поверхность раздела «жидкость — твердое тело», уравнения (1.2.23), (1.2.35).

Так приложение уравнения (1.2.34) к уравнению Юнга для случая смачивания неполярной жидкостью поверхности полимерного материала позволяет получить уравнение, известное как уравнение Фоукса, при

. (1.2.58)

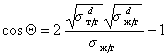
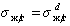
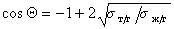
Если жидкости неполярны и , то уравнение (1.2.58) переходит в уравнение

. (1.2.59)

Уравнение (1.2.59) Зисман предложил использовать для определения поверхностного натяжения твердых тел. Очевидно, что при 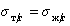cosQ =1, а угол смачивания будет равен нулю (Q = 0), т.е. наступает полное смачивание.

Естественно, что метод Зисмана ограничен некоторыми условиями, в частности, из уравнения (1.2.57) следует, что полное смачивание возможно при дисперсионной неразличимости твердого тела и жидкости, т.е. при А₂₃₂= А₁₂₃.

В действительности такого условия никогда невозможно достигнуть хотя бы потому, что если жидкость и твердое тело будут иметь одинаковый химический состав, их постоянные Гамакера будут различаться из-за различий в плотности.

Другое ограничение, связанное с применением метода Зисмана, основано на том, что использовать для измерения краевых углов смачивания следует лишь неполярные жидкости. Наиболее целесообразно применять гомологические ряды жидкостей. При величине поверхностного натяжения жидкостей более 35 мДж/м 2 метод Зисмана уже дает высокую погрешность, так как необходимо учитывать вклад полярных сил, которые в отличие от дисперсионной составляющей могут иметь и отрицательное значение. С другой стороны, приложение для смачивания твердых тел полярными жидкостями уравнения Ву (1.2.36) позволяет рассчитать полярную составляющую поверхностного натяжения жидкости, если для одной из неполярных жидкостей измерить краевой угол смачивания. Для расчета используют уравнение

Рис. 1.25. Зависимость смачивания поверхностей от поверхностного натяжения жидкостей. Материал поверхности: 1- FC-721; 2- ПТФЭ (тефлон); 3 — полиэтилен

. (1.2.60)

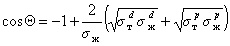
Этот метод позволил разделить величину поверхностного натяжения жидкостей на полярную и дисперсионную компоненты и определить поверхностное натяжение многих волокнообразующих полимеров.

Пример зависимости косинуса угла смачивания поверхности пленок различными жидкостями приведен на рис.1.25. Для описания этих зависимостей Зисман предложил использовать эмпирическое уравнение

, (1.2.61)

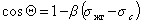
где bэмпирическая постоянная, s_с – «критическое» поверхностное натяжение твердого тела, при котором происходит полное смачивание твердого тела жидкостью. Очевидно, что cos Q =1 при условии s_жг = s_с .

Как мы обсуждали выше, этот критерий в известной мере является условным, хотя и отражает энергетическое состояние поверхности твердого тела.

Реальное значение поверхностного натяжения твердого тела экспериментально определить невозможно, также как и рассчитать его теоретически. В этой связи метод Зисмана нашел широкое применение в практике исследования полимерных материалов, а также полимерных покрытий тканей, используемых в качестве отделочных материалов

Видео:Урок 13 (осн). Взаимодействие молекул. Смачивание и несмачиваниеСкачать

Лако-красочные материалы — производство

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Технологии и оборудование для изготовления красок, ЛКМ

Видео:Матвеенко В. Н. - Коллоидная химия - Поверхностное натяжениеСкачать

ЯВЛЕНИЯ СМАЧИВАНИЯ

К явлению адсорбции близки явления смачивания, также опре­деляющиеся интенсивностью взаимодействия между молекулами » различных веществ. Рассмотрим явления смачивания на примере капли жидкости, нанесенной на поверхность твердого тела, хотя» конечно, можно говорить и о смачивании жидкости жидкостью.

Смачивание и краевой угол. Если молекулы жидкости взаимо­действуют с молекулами твердого тела сильнее, чем между собою, то жидкость растекается по поверхности или, как говорят, смачи­вает ее. Растекание происходит до тех пор, пока жидкость не по-

Кроет всю поверхность твердого тела или пока слой жидкости не станет мономолекулярным. Такой случай называется полным смачиванием. Он наблюдается, например, при нанесении капли воды на поверхность чистого стекла.

Если молекулы жидкости взаимодействуют друг с другом зна­чительно сильнее, чем с молекулами твердого тела, растекания не произойдет. Наоборот, жидкость соберется на поверхности в каплю, которая, если бы не действовала сила тяжести, имела бы почти сферическую форму. Случай, близкий к этому, наблюдается при нанесении капли ртути на любую неметаллическую поверх­ность.

Между этими двумя крайними случаями в зависимости от со­отношения интенсивности молекулярных сил, действующих, с од­ной стороны, между молекулами жидкости и, с другой — между

Рис. VI, 7. Различные случаи неполного смачивания: о —9 90°.

Молекулами жидкости и твердого тела, возможны переходные слу­чаи неполного смачивания, когда капля образует с поверхностью твердого тела определенный равновесный угол, называемый крае­вым углом, или углом смачивания.

На рис. VI, 7 изображены капли, образующие на твердой по­верхности острый краевой угол (0 9О°). Следует иметь в виду, что краевой угол, образуемый каплей на поверхности твердого тела, всегда измеряют со стороны жидкости. Полного несмачивания, т. е. случая, когда краевой угол равен 180°, практически никогда не наблюдается, так как между жидкостью и твердым телом все­гда действуют силы притяжения, хотя бы и очень малые.

Ниже приведены значения краевого угла, образуемого водой на поверхности различных твердых тел в атмосфере воздуха:

Кварц Малахит Галенит Графит Тальк Сера Парафин

0° 17° 47° 55—60° 69° 78° 106°

Смачивание жидкостью твердого тела можно объяснить как результат действия сил поверхностного натяжения. Рассмотрим пример неполного смачивания, изображенный на рис. VI, 8. Оче­видно, периметр смачивания, или окружность, капли является гра­ницей взаимодействия трех сред — жидкости /, воздуха 2 и твер­дого тела 3. Эти среды имеют разграничивающие их поверхности: поверхность ЖИДКОСТЬ — воздух С поверхностным натяжением (Ті, 2, поверхность воздух — твердое тело с поверхностным натяжением 02, з и поверхность жидкость — твердое тело с поверхностным на­тяжением (Ті, з. Таким образом, на единице длины периметра сма­
чивания действуют три силы ai, 2, 02,3 и 01,3, обозначенные на рисунке соответствующими векторами и направленные перпенди­кулярно к отдельным элементам окружности и касательно к соот­ветствующей поверхности раздела. При образовании равновесного краевого угла 0 все три силы должны уравновешивать друг друга. Силы 02, з и сті, з действуют в плоскости поверхности твердого тела. Сила же ai, 2 направлена к поверхности под углом 0. Однако по­скольку точка приложения трех сил может только передвигаться

Рис. VI, 8. Зависимость между краевым углом и поверхностными натяжениями 0i,2, 02,3 и crlj3:

1 — жидкость; 2—воздух; 3—твердое тело.

ПО поверхности, НО не может ОТ нее оторваться, вместо СИЛЫ 01, 2 следует ВЗЯТЬ ее проекцию на ПЛОСКОСТЬ, Т. е. 01, 2 cos 0. Тогда усло­вие равновесия сил выразится уравнением Юнга:

02, 3 = 01, 3 + 01, 2 cosG (VI, 8)

Решив это уравнение относительно cos 0, получим:

Помимо приведенного выше «силового» вывода, уравнение Юнга можно вывести и из термодинамических соображений. Приводим этот вывод пй Адам-» со ну.

Представим себе, что жидкость продвинулась по поверхности на весьма малое расстояние и покрыла поверхность твердого тела, равную As. Учитывая, что удельные межфазиые энергии численно равны соответствующим значениям поверхностного натяжения, изменение свободной поверхностной энергии ДF в- этом случае будет равно:

ДF = As (о,, з — о2) з) + AsOj, 2 cos (9 — Д9)

AF/As — 01, з — 02, з + 01,2 cos (9 — Д9)

При равновесии lim AF/As = О о

01, 3 — 02, 3 + 01, 2 COS 9 = О

02, 3=01, 3+01, 2 COS 9 . 02, 3 — 01, 3

Величину cos 6, характеризующую способность жидкости сма­чивать поверхность, принято называть смачиванием и обозначать

Через В. Очевидно, что при полном смачивании (0 = 0) В = +1» а гипотетическому случаю полного несмачивания (0 = 180°) отве­чает В — —1. Поскольку жидкость тем лучше смачивает твердое тело, чем меньше взаимодействие между ее молекулами, неполяр­ные жидкости с малым поверхйостным натяжением обычно хо­рошо смачивают поверхность. Например, углеводороды с поверх­ностным натяжением порядка 20—30 эрг/см2 практически смачи­вают все твердые тела; вода с поверхностным натяжением 72,75 эрг/см2 (при 20 °С) смачивает лишь некоторые тела, напри­мер стекло, кварц, неорганические соли; ртуть с поверхностным натяжением 475 эрг/см2 смачивает только некоторые металлы.

Смачивание является процессом, при котором в системе из трех соприка­сающихся фаз происходит уменьшение свободной энергии. В самом деле, пусть очень тонкий слой жидкости 1 растекается по поверхности твердого тела 3, ко­торое находится в среде 2, и пусть площадь, покрытая жидкостью, в результате этого увеличивается на As При этом:

1) поверхность твердого тела, соприкасающегося со средой 2, уменьшится яа As, в результате чего поверхностная энергия системы уменьшится на сгг, 8As;

2) поверхность, которой жидкость 1 соприкасается со средой 2, увеличится яа As, благодаря чему поверхностная энергия возрастает на 0i, IAs,

3) площадь межфазиой поверхности между жидкостью 1 и твердым телом 3 возрастает на As, вследствие чего поверхностная энергия системы увеличится Нй оч, SAs.

Таким образом, общее изменение свободной поверхностной энергии F при растекании жидкости будет:

ДҐ/Д5=0,,з + 0І,2-02,3 (VI, 10)

Но из уравнения (VI, 8) следует, что яри растекании жидкости, полностью сма­чивающей поверхность (Gos6 = 1), должно соблюдаться условие

01.3 + 01,2-02,3 0, поверхность называют гидрофильной. Согласно урав­нению (VI, 9) этот случай имеет место при условии, когда 02, з > > 0. Избирательное смачивание во­дой наблюдается обычно,’когда разность полярностей между водой и твердым веществом меньше, чем между неполярным углеводоро­дом и твердым веществом. К веществам с гидрофильной поверх­ностью относятся вещества с сильно выраженным межмолекулярным взаимодействием, например кварц, стекло, корунд, гипс, малахит, т. е. силикаты, карбонаты, сульфаты, а также окиси и гидраты окисей металлов. Из органических веществ в качестве веществ с гидрофильной поверхностью можно указать целлюлозу.

Если же твердое тело лучше смачивается неполярным углево­дородом, т. е. если для воды 9 > 90°, а значение В = cos 9 90 °С.

Определение краевого угла. Для измерения краевого угла, об­разуемого жидкостью на твердом теле, на его поверхность наносят небольшую каплю жидкости и с помощью пучка света, направлен­ного параллельно поверхности, проектируют боковое изображение капли на экран, затем на экране очерчивают контур капли, сидя­щей на поверхности твердого тела, и через точку, в которой со­прикасаются все три фазы, проводят касательную к контуру капли. Угол наклона этой касательной и есть краевой угол.

Для измерения краевого угла, образуемого двумя несмешиваю — щимися жидкостями на поверхности твердого тела, пластинку из исследуемого вещества погружают в стеклянную кйвету с более легкой жидкостью и затем на поверхность пластинки осторожно с помощью пипетки наносят каплю более тяжелой жидкости. Да­лее поступают так же, как и в предыдущем случае.

Помимо этого простейшего, но не очень точного метода опре­деления краевого угла есть и другие, более точные, но и более сложные методы, которые рассматриваются в практикумах по кол­лоидной химии.

Следует заметить, что определить истинное значение краевого угла часто затруднительно по следующим причинам.

1. На краевой угол могут влиять следы веществ, загрязняющих поверхность. Резкое изменение смачивания происходит уже при образовании на поверхности мономолекулярного слоя, загрязняю­щего вещества, для чего нужны ничтожные его количества. По данным некоторых исследователей, на смачивание поверхности мо­жет сказываться даже контакт этой поверхности в течение некото­рого времени с воздухом промышленных городов, всегда содержа­щим следы углеводородов.

2. Многие вещества, например металлы, хорошо окисляются и на их поверхности образуется тончайшая, трудно обнаруживаемая пленка окислов. Эта пленка также может сильно влиять на сма­чивание. Поэтому для определения краевого угла надо брать не­загрязненные и неокислившиеся поверхности.

3. Поверхности обычно хорошо адсорбируют воздух. Естествен­но, что адсорбированный воздух замедляет процесс растекания жидкости по твердому телу, так как для вытеснения воздуха с по­верхности и установления равновесного краевого угла требуется определенное время. Подобное замедление установления равновес­ного краевого угла называется гистерезисом смачивания. Во мно­гих случаях равновесное значение краевого угла из-за гистерезиса может и не достигаться вовсе.

Явление гистерезиса наглядно проявляется в том, что краевой угол очень часто зависит от условия его образования. А именно, если каплю жидкости прижать к поверхности твердого тела, то краевой угол будет меньше, чем в том случае, если каплю осто­рожно нанести на поверхность. В капиллярах с неполностью сма­чиваемыми стенками вследствие гистерезиса жидкость подни­мается на различную высоту в зависимости от того, поднимается ли жидкость свободно по капилляру, или же сначала заполняют капилляр и затем дают стечь жидкости до достижения равновес­ного положения.

Гистерезис является также причиной того, что краевой угол, образуемый при натекании жидкости, обычно гораздо больше, чем при оттекании. Последнее явление можно наблюдать, когда капли дождя стекают «не по слишком чистому оконному стеклу, при этом капли как бы задерживаются и снизу образуют гораздо больший краевой угол, чем сверху,

С целью устранения гистерезиса, происходящего в результате адсорбции воздуха, методику определения краевого угла можно видоизменить следующим образом. Пластинку твердого вещества вводят в стеклянную кювету с жидкостью и после полного сма­чивания ее поверхности устанавливают в горизонтальном положе­нии. Затем под пластинку, не вынимая ее из жидкости, с помощью пипетки с загнутым концом вводят пузырек воздуха. Далее опре­деление краевого угла, который и в этом случае измеряют со сто­роны жидкости, проводят так, же, как было описано выше[9].

4. На смачивание твердого тела может влиять шероховатость поверхности, причем чем больше шероховатость, тем резче про­являются свойства поверхности, обуславливающие притяжение или отталкивание воды. Подобное влияние можно объяснить тем, что при 0 90°, то жидкость но проникает в углубления, что ухудшает смачивание шероховатой поверхности. Иными словами, гидрофильной поверхности шерохо­ватость придает как бы еще большую гидрофильность, а шерохо­ватость гидрофобной поверхности делает ее еще более гидрофоб­ной. Для исключения влияния микрорельефа поверхность иссле­дуемого твердого тела должна быть возможно более гладкой.

Венцель первый указал путь, позволяющий учитывать влияние шерохова­тости поверхности на ее смачивание жидкостью. Для этого входящие в расчет­ное уравнение (уравнение Юнга) поверхностные натяжения Ог, з и с,, з следует умножить на так называемый фактор шероховатости, т. е. на отношение факти­ческой поверхности раздела к поверхности твердого тела, если бы она была гладкой [10]. В результате вместо уравнения Юнга надо написать:

5. На краевой угол могут влиять условия образования поверх­ности. Так, поверхность стеариновой кислоты, полученная охла­ждением ее расплава на воздухе, гидрофобна. Поверхность же стеариновой кислоты, полученная охлаждением ее расплава на границе со стеклом, оказывается гидрофильной. Это явление мож­но объяснить тем, что в первом случае наружу слоя кислоты (в воздух) обращены, главным образом, гидрофобные углеводо­родные радикалы стеариновой кислоты, а во втором случае, бла­годаря действию поверхности полярного стекла на расплав, на­ружу обращены полярные гидрофильные карбоксильные группы.

Вообще благодаря определенной ориентации молекул вещества в поверхностном слое можно говорить о поверхностной и объемной гидрофильности или гидрофобности вещества. В. А. Пчелиным было показано, что поверхность животного во­лоса гидрофобна, в то время как само вещество волоса гидро­фильно.

На практике наиболее важен случай, когда смачивающей жид­костью является вода. Плохо смачиваются водой неполярные ве­щества, например поверхности, покрытые углеводородами. Для улучшения смачивания водой обычно применяют смачиватели — растворимые, хорошо адсорбирующиеся, поверхностно-активные вещества, понижающие поверхностное натяжение на границе твердое тело — жидкость и одновременно на границе жидкость — воздух. При нанесении на поверхность смачивателя краевой угол, являющийся мерой смачивания, согласно уравнению (VT, 9), уменьшается в результате снижения значений ai, 3 и а,, 2, а сма­чивание соответственно возрастает.

Обычно молекулы смачивателей дифильны, что характерно для всякого поверхностно-активного вещества, и адсорбируются на поверхности воды, ориентируясь углеводородными цепями наружу в воздух, благодаря чему на поверхности воды создается как бы пленка углеводорода. Этим и объясняется понижение поверхност­ного натяжения раствора и повышение смачивающей способности до значений, соответствующих поверхностным натяжениям орга­нических неполярных жидкостей.

Интересным свойством монослоев поверхностно-активных ве­ществ является их способность переходить из раствора на твердую поверхность и образовывать на этой поверхности полимолекуляр­ные слои. Это свойство было обнаружено еще Блоджетт на сле­дующем опыте.

В мономолекулярный плотно упакованный слой молекул по­верхностно-активного вещества, образованный на поверхности воды, осторожно вводят в вертикальном„положении стеклянную пластинку. При погружении этой пластинки гидрофильная поверх­ность ее покрывается мономолекулярным слоем поверхностно — активного вещества, причем полярная часть молекул вещества, естественно, будет обращена к полярной поверхности стекла и поверхность пластинки, таким образом, станет гидрофобной. После этого пластинку вместе с адсорбированным на ней слоем поверх­ностно-активного вещества осторожно извлекают из раствора. При этом на пластинке, уже адсорбировавшей мономолекулярный слой поверхностно-активного вещества, адсорбируется второй слой того же вещества, причем неполярные радикалы молекул этого слоя обращены к неполярным радикалам первого слоя, т. е. по направ­лению к пластинке. В результате на поверхности пластинки обра­зуется бимолекулярный слой молекул, обращенных друг к другу неполярными радикалами, а поверхность пластинки станет снова гидрофильной. Неоднократно повторяя эту операцию, можно пе­ренести на пластинку значительное число слоев поверхностно — активного вещества, делая поочередно поверхность пластинки то гидрофобной, то гидрофильной.

Практическое значение смачивания. Смачивание имеет большое значение для успешного проведения ряда важнейших технологиче­ских процессов. Например, в текстильной технологии хорошее сма­чивание волокна или тканей является важным условием для кра­шения, беления, расшлихтовки, пропитки, стирки и т. д. Совер­шенно понятна роль смачивания для эффективного применения инсектофунгисидов, поскольку листья растений и шерстяной по­Кров животных всегда в той или иной степени гидрофобны. Боль­шое значение имеет смачивание и в типографском деле. Смачива­ние соответствующими жидкостями металлов и неметаллических тел ускоряет и облегчает иХ механическую обработку (резание, сверление, шлифовку, полировку). Бурение нефтяных скважин в Горных породах также облегчается, если применять специальные бурильные растворы, содержащие смачиватели. При лужении, спайке, сварке металлов, а также склеивании различных твердых тел необходимо прежде всего хорошее смачивание их поверхности. Наконец, на явлениях избирательного смачивания основано обо­гащение руд — флотация. Рассмотрим в качестве примера роль

Смачивания в таких процессах, как стирка, пропитка и фло­тация.

Целью стирки является удаление с поверхности твердого теуіа, обычно волокна или ткани, прилипших к ней загрязнений — шер­стяного жира, шлихты, сажи, пыли, белковых веществ и т. д. При стирке поверхность раздела волокно — загрязнение заменяется на поверхности раздела волокно — раствор моющего вещества и за­грязнение— раствор моющего вещества. Отличие процессов, ле­жащих в основе стирки, от избирательного смачивания заклю­чается только в том, что роль первой жидкости играет твердое или полутвердое загрязнение.

Рассмотрим процесс стирки на примере удаления жидкого угле­водорода (жира) с поверхности ткани с помощью обычного мыла. Задача технолога при проведении этого процесса — как можно

Рис. VI, 9. Схема отмывания углеводорода при стирке:

А—жидкость, смачивающая поверхность; б—жидкость, не смачивающаи по­верхность.

1—мыльный раствор; 2—углеводород; 3— ткаиь; 4 —гидрофильный слой мою­щего вещества.

Больше уменьшить поверхностное натяжение на границах раздела моющий раствор — загрязнение и моющий раствор — волокно. По­верхностные натяжения этих поверхностей уменьшаются в резуль­тате адсорбции мыла на поверхности жира и ткани, причем ад­сорбция происходит, конечно, таким образом, что молекулы мыла обращаются полярной частью в воду, неполярной — к загрязнению или волокну. Тогда под влиянием неизменившегося поверхностного натяжения на границе твердое тело — загрязнение жир соберется в каплю, которую легко можно удалить с поверхности волокна путем даже незначительного механического воздействия. Происхо­дит отмывание, заключающееся § резком увеличении В — cos 0 (для воды), т. е. в уменьшении краевого угла. Это наглядно пока­зано на рис. VI, 9.

При стирке моющее вещество, адсорбируясь как на поверхно­сти ткани 3, так и на поверхности загрязняющей ткань частицы углеводорода 2, образует на них гидрофильный слой мыла 4. Этот Слой способствует отделению частицы загрязнения от ткани, так как улучшение смачиваемости отмываемой поверхности водой в условиях избирательного смачивания означает понижение смачи­вания ее углеводородом. Кроме того, образовавшийся на капель­ках углеводорода слой гидратированных частично ионизированных
Молекул мыла придает устойчивость возникшей эмульсии и этим способствует удалению загрязнения вместе с моющим раствором в конце стирки.

Следует заметить, что на поверхности отбеленной гидрофиль­ной ткани, благодаря полярности целлюлозы, адсорбирующиеся молекулы мыла могут ориентироваться полярными группами к волокну и неполярными углеводородными радикалами — в мою­щий раствор. Казалось бы, в этом случае должна происходить гидрофобизация поверхности, понижающая эффект стирки. Од­нако имеются данные, что при использовании достаточно концен­трированных растворов мыла после возникновения первого слоя молекул на ткани образуется второй слой мыла, молекулы кото­рого ориентированы противоположным образом, т. е. полярной группой в моющий раствор. Таким образом, и в этом случае на­блюдается гидрофилизация поверхности ткани.

П. А. Ребиндер считает, что обязательным условием для мою­щего действия является также достаточная механическая проч­ность и вязкость гидратированных адсорбционных слоев моющего вещества. С одной стороны, такие слои на границе моющий рас­твор— воздух способствуют пенообразованию, играющему при стирке важную роль. С другой стороны, образование прочных гид­ратированных адсорбционных слоев вокруг частиц жира обеспе­чивает эмульгирование отмытых загрязнений и препятствует их вторичному оседанию на волокне [11].

Процессом, в известной степени обратным стирке, является пропитка тканей с целью повысить их водонепроницаемость при сохранении воздухопроницаемо­сти (так называемая пористая водоотталкивающая пропитка). Задача технолога при проведении этого процесса заключается в образовании на поверхности от­дельных волоконец ткани тонких пленок, на которых вода образует большой краевой угол. С этой целью ткани пропитывают растворами или дисперсиями гидрофобных, так называемых водоотталкивающих веществ. В качестве таких веществ можно использовать ацетат алюминия, мыла поливалентных металлов, парафин, асфальт, нефтяные остатки, кремнийорганические соединения и смеси этих веществ. Иногда пропитку тканей с целью повышения их водонепроницае­мости проводят в два приема. Например, ткань пропитывают сначала диспер­сией парафина, содержащей мыло в качестве эмульгатора, а затем раствором ацетата алюминия, при этом частицы парафина отлагаются на волокне в ре­зультате коагуляции.

После пропитки ткань высушивают, и при этом на волоконцах материала образуются пленки водоотталкивающих веществ. При пропитке ткани диспер­сией частицы водоотталкивающего вещества отлагаются на поверхности волоко­нец дискретно. Однако в условиях последующей сушки при повышенной темпе­ратуре гидрофобное вещество обычно плавится и растекается по волокну.

В результате пропитки поверхность капилляров ткани становится гидро­фобной, несмачиваемой водой. Продвижению воды по такому капилляру ме­шает большое поверхностное натяжение на границе вода — гидрофобизированная поверхность, которое стремится уменьшить поверхность соприкосновения между водой и стенкой капилляра и не позволяет воде течь по стенкам капилляра. Поэтому вода, проникая в устье капилляра, не смачивает его стенки, а образует выпуклый мениск, как это показано на рис. VI, 10. Искривленная поверхность
этого мениска под действием поверхностного натяжения стремится стянуться и стать плоской, при этом возникает направленное вверх давление. Это давле­ние уравновешивает давление воды, стремящейся проникнуть в капилляр. По­нятно, что чем выше поверхностное натяжение и чем уже капилляр, тем больше должно быть давление, которое может протолкнуть воду через капилляр. Следо­вательно, для получения ткани с высокой водонепроницаемостью нужно, чтобы

Гидрофобизируемая ткань была достаточно плотной и чтобы в ней не содержалось поверх­ностно-активных веществ (остатков эмульгато­ров эмульсии, которой производилась пропит­ка)*.

Рис. VI, 10. Несмачивание во­дой капилляра гидрофобизиро — ванной ткани.

На явлениях смачивания и несма­чивания, как уже указывалось, ос­нован и процесс флотации — метод обогащения полезных ископаемых, по­лучивший в настоящее время исклю­чительно широкое применение. В осно­ве этого метода лежит использование различий в смачивании разделяемых частиц водой. Чтобы уяснить себе принцип, на котором основана флотация, рассмотрим поведение достаточно малых гидрофобных и гидрофильных минеральных частиц на границе раздела вода — воздух или вода — масло.

Гидрофильные частицы смачиваются водой и под действием поверхностного натяжения на границе вода — воздух или вода — масло частица втягивается в воду. Наряду с силой поверхностного

Рис. VI, 11. Разделение гидрофильных (а) и гидрофобных (б) частиц путем флотации: 1—водная фаза; 2— воздух илн масло; 3—твердое тело.

Натяжения на частицу действует и сила тяжести. В результате частица, смачиваемая водой, целиком перейдет в водную фазу и потонет.

Гидрофобные частицы вода не смачивает, и под действием1 по­верхностного натяжения на границе вода — воздух или вода — масло частица может остаться на границе раздела, если только она не слишком велика и сила тяжести не превысит флотационную силу. Схематически эти оба случая изображены на рис. VI, 11. Понятно, что измельчая минерал до нужной дисперсности, всегда

Можно подобрать размер частиц, при котором частицы будут оста­ваться на поверхности, поскольку при дроблении сила тяжести уменьшается прямо пропорционально кубу радиуса частицы, а флотационная сила снижается прямо пропорционально первой сте­пени радиуса. Однако слишком высокая дисперсность может ока­заться вредной — мелкие частицы подвержены интенсивному броу­новскому движению, что уменьшает вероятность их закрепления на границе вода — воздух или вода — масло.

Флотационное обогащение руд полезных ископаемых основано на том, что сернистые соединения, в виде которых металлы обычно находятся в руде, обладают большей гидрофобностью, чем пустая порода, например кварц. Практически флотационное разделение руды никогда не проводят простым введением измельченной руды в воду, поверхность — которой граничит с воздухом или маслом. В таком виде флотационный процесс слишком неэффективен. В на­стоящее время широкое применение получила так называемая Пенная флотация. Она заключается в том, что в суспензию мине­рала— флотационную пульпу — тем или иным способом вводят пу­зырьки воздуха. При всплывании пузырьки собирают по своей по­верхности те частицы руды, на’ которых вода образует большой краевой угол. В результате на поверхности пульпы образуется минерализованная пена. Эту пену самотеком или с помощью спе­циальных гребков удаляют с поверхности пульпы в виде концен­трата. руды. Хорошо смачиваемые водой частицы пустой породы не прилипают к пузырькам, оседают на дно и образуют отходы флотации, так называемые «хвосты».

Оптимальный размер зереи минерала при флотации 0,15— 0,01 мм. Однако при флотации каменного угля и самородной серы частицы минерала могут быть И более крупными (0,5—1 мм). Ве­совое отношение руды к воде в пульпе обычно лежит в пределах от 1 : 4 до 1 : 2.

Рассмотрим в самых общих чертах термодинамику пеиной флотации. Для этого вычислим изменение свободной энергии системы при пениой флотации. До флотации для свободной межфазной энергии F0 системы можно написать следующее уравнение:

Fo = Oi, 2S1.2 + ffi, s«i,3 (VI, 12)

Где оч. 2 и Сті,3 — удельная поверхностная энергия (численно равная межфаз­ному натяжению) на границе водная среда — воздух и водная среда — флоти­руемое вещество соответственно; si, 2 и s 1,3 — соответствующие межфазные по­верхности. В результате флотации свободная энергия в расчете на единицу по­верхности контакта флотируемой частицы с воздухом равна:

^1 = 2 + a1.3-a2,3 (VI, 14)

Согласно уравнению (VI, 8) ■

Oi. a — Ог, з = — a,, 2 cos 0 (VI, 15)

Подставляя это уравнение в уравнение (IV, 14), получим:

— AF==o,,2 — oi.2cose = ai,2(l — cosB) = ff,,2 (1 — В) (VI, 16)

Вероятность флотации W связана с изменением свободной энергии следующим образом:

Следовательно, вероятность флотации частиц возрастает с увеличением поверх­ностного натяжения на границе вода — воздух и с уменьшением смачивания водной фазой флотируемых частиц.

Обычно разность в гидрофобности поверхности частиц ценного минерала и пустой породы сравнительно невелика. Поэтому для повышения эффективности флотации почти всегда применяют так называемые коллекторы, или собиратели. В качестве коллекторов используют органические вещества с дифильной молекулой, спо­собные адсорбироваться на поверхности частиц ценного минерала таким образом, что полярная часть молекулы обращается к ад­сорбенту, а углеводородный радикал — наружу. В результате этого гидрофобность частиц минерала возрастает и флотационный про­цесс протекает интенсивнее. Наиболее часто в качестве коллекто­ров применяют ксантогенаты RO—(где R — углеводород­ам

Ный радикал, М — щелочной металл). Имеются данные, что ксан­тогенаты не просто адсорбируются поверхностью частиц сернистых металлов, но вступают с ними в химическое взаимодействие.

При флотации несульфидных минералов в качестве коллекто­ров обычно применяют жирные кислоты и их мыла. Ионогенные группы этих коллекторов всегда обращены к твердой фазе (Solid), поэтому эти группы принято называть солидофильными. Особенно пригодны такие коллекторы для солеобразных минералов, в со­став которых входят катионы щелочноземельных металлов Са2+, Mg2+, Sr2+. В кристаллических решетках этих минералов преобла­дает ионная связь, и их катионы активно взаимодействуют с хи­мически адсорбирующимися поверхностно-активными ионами RCOO — кислоты или мыла. На закреплении коллекторов на по­верхности

флотируемых частиц сказывается также и влияние длины углеводородного радикала, а именно, взаимодействие угле­водородных цепей друг с другом способствует образованию4 ад­сорбционной пленки и чем сильнее такое взаимодействие, тем прочнее закрепляются адсорбционные слои коллектора на поверх­ности минерала.

Для неполярных неметаллических минералов (графит, сера, тальк, ископаемый уголь), которые плохо смачиваются водой, нет необходимости в сильных коллекторах. Для них обычно исполь­зуют мало растворимые в воде коллекторы, например масла. При флотации расходуется сравнительно мало коллектора — на 1 т руды берут обычно только сотни граммов реагентов. Это указывает на то, что для улучшения флотации на поверхности минеральных частиц достаточно образования тончайшего мономолекулярного слоя, иногда даже ненасыщенного.

Помимо коллекторов при флотации применяют пенообразова­тели и регуляторы.

Пенообразователи нужны для получения достаточно (но не слишком) стой­кой минерализованной пены. Пенообразователи не должны заметно изменять смачивание флотируемых частиц, а должны адсорбироваться на границе пузы­рек воздуха — водная фаза. Этими свойствами обладают алифатические спирты, так как группа —ОН обычно слабо закрепляется на поверхности минеральных частиц и в то же время хорошо адсорбируется на границе раствор — газ, бла­годаря поверхностной активности спирта, способствуя тем самым вспениванию.

При выборе пенообразователей следует избегать веществ, сильно понижаю­щих поверхностное натяжение, так как иначе пенз окажется пустой, т. е. не содержащей ценного минерала или содержащей его в очень малом количестве.

Регуляторы применяют для регулирования избирательного действия коллек­торов. В одних случаях регулятор, действуя непосредственно на поверхность минерала, облегчает взаимодействие с ним коллектора и тем улучшает флота­цию. Такой регулятор является активатором флотации. В других случаях, наобо­рот, регулятор затрудняет взаимодействие минерала с коллектором, что по­давляет флотацию этого минерала. В этом случае регулятор можно назвать де­прессором. Примером активатора при флотации является сульфид натрия, улуч­шающий флотацию сернистых металлов с помощью ксантогенатов. В качестве депрессора может служить жидкое стекло, ухудшающее флотацию силикатных минералов.

Флотацию можно применять не только для выделения из по­лезного ископаемого какого-нибудь одного продукта, но и для разделения ряда продуктов. Такая флотация называется селектив­ной, она осуществляется обычно с помощью регуляторов. Приме­ром селективной флотации может служить флотация свинцово — цинковых руд. При этом сначала получают свинцовый концентрат, вводя для этого в пульпу депрессоры, предотвращающие флота­цию цинковых минералов, затем с помощью активаторов улучшают флотационную способность цинковых минералов и добиваются перехода их в пену, получая таким образом цинковый концентрат.

Применение флотации для обогащения полезных ископаемых непрерывно расширяется. Флотация используется для обогащения сульфидных и ряда руд цветных металлов, например свинцово — цинковых, медных, медно-цинковых, молибденовых, железных, оло­вянных и руд редких металлов. Флотация применяется для обо­гащения таких ископаемых, как сера, графит, уголь, а также руд, содержащих апатит, плавиковый шпат, барит и т. д. Значение флотации особенно возрастает вследствие того, что она позволяет использовать тонко вкрапленные в горные породы руды, запасы которых неисчерпаемы.

🔍 Видео

Коллоидная химия. Лекция 1. Физико-химия поверхностных явленийСкачать

Галилео. Эксперимент. Поверхностное натяжениеСкачать

Урок 209. Закон Гука. Модуль ЮнгаСкачать

Поверхностные явленияСкачать

Капиллярный эффект.Мениск (видео 4) | Силы межмолекулярного взаимодействия | ХимияСкачать

Урок 202. Давление под искривленной поверхностью жидкости. Формула ЛапласаСкачать

5.1. Адсорбция. Классификация адсорбцииСкачать

Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать

Урок 205. Задачи на капиллярные явленияСкачать

А что, если..? Капиллярные явления/And what if..? Capillary effectСкачать