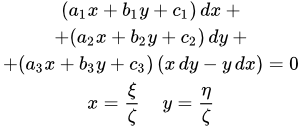Уравнение якоби для дифференциальных уравнений

(f_1,f_2,dots,f_n)= /+ /+dots+ / . $$

Пример. Якобиан системы двух функций $ $ равен

Теорема [Якоби]. Если $ A_,dots,A_ $ — алгебраические дополнения элементов $ j_ $-й строки якобиана, то

Функциональная зависимость

Следующая теорема и ее следствия являются прямыми обобщениями соответствующих результатов из линейной алгебры.

Теорема. Якобиан системы функций $ < f_,f_2,dots,f_n > $ тождественно равен нулю в некоторой области $ mathbb_ $:

$$ frac equiv 0 mbox mbox mbox X in mathbb $$ тогда и только тогда, когда между этими функциями имеется функциональная зависимость в $ mathbb $, т.е. существует функция $ G(y_1,y_2,dots,y_n) notequiv 0 $ такая, что $$ G(f_1(X),f_2(X),dots,f_n(X))equiv 0 mbox mbox mbox X in mathbb . $$

Приведем соображения, показывающие необходимость обращения якобиана в нуль для существования функциональной зависимости в системе функций $ $. Дополнительно предположим, что у функции $ G $ существуют частные производные по ее аргументам. Продифференцируем тождество $ G(f_1(X),f_2(X),dots,f_n(X))equiv 0 $ по $ x_1,dots,x_n $. Получим систему тождеств $$ left<begin frac frac+ & frac frac+ &dots + frac frac & equiv 0, \ dots & & & dots \ frac frac+ & frac frac+ &dots + frac frac & equiv 0; end right. $$ здесь после вычисления производных $ $ следует произвести подстановку $ y_1=f_1(X),dots,y_n=f_n(X) $. Получившуюся систему можно рассматривать как линейную однородную относительно этих последних выражений. Хотя бы одна из них не должна быть тождественно нулевой (в противном случае функция $ G $ не содержала бы ни одной функции $ f_j $). Но тогда для совместности системы необходимо, чтобы ее определитель был равен нулю. Этот определитель, с точностью до транспонирования, совпадает с якобианом.

Пример. Являются ли полиномы

$$ f_1=x_1+x_2+x_3-1,quad f_2=x_1x_2+x_1x_3+x_2x_3-2,quad f_3=x_1^2+x_2^2+x_3^2+3 $$ функционально зависимыми?

Решение. $$ frac= $$ $$ = left| begin 1 & 1 & 1 \ x_2+x_3 & x_1+x_3 & x_1+x_2 \ 2x_1 & 2x_2 & 2x_3 end right| = 2 left| begin 1 & 1 & 1 \ x_2+x_3 & x_1+x_3 & x_1+x_2 \ x_1 & x_2 & x_3 end right|= $$ $$ = left| begin 1 & 1 & 1 \ x_1+x_2+x_3 & x_1+x_2+x_3 & x_1+x_2+x_3 \ x_1 & x_2 & x_3 end right|equiv 0 $$ (мы воспользовались здесь свойствами 4 и 5 определителя, выписанными ☞ ЗДЕСЬ ). Ответ оказывается положительным: рассматриваемые полиномы являются функционально зависимыми. В данном примере эта зависимость сравнительно просто «отлавливается» наметанным взглядом: $$(f_1+1)^2-2(f_2+2)-(f_3-3) equiv 0 . $$ ♦

Если какие-то $ mathfrak r $ функций системы $ < f_, dots, f_n > $ связаны в $ mathbb $ функциональным соотношением

$$ H(f_, dots, f_<j_>) equiv 0 , $$ то любой минор порядка $ mathfrak r $ якобиана, выбранный из соответствующих строк, будет тождественно равен нулю в $ mathbb_ $.

Пусть $ mathfrak r_ $ обозначает ранг матрицы Якоби системы функций $ <f_1,dots,f_> $ по переменным $ x_,dots,x_n $. Если минор этой матрицы

$$ frac<D(f_1,dots,f_)> $$ отличен от нуля в $ mathbb_ $, то функции $ f_1,dots,f_ $ функционально независимы в $ mathbb $, а все оставшиеся функции системы (при условии $ mathfrak r непрерывная функция $ varphi (y) $ такая, что $$ f(varphi(y)) equiv y, varphi(y_0)=x_0 , . $$ В этой окрестности функция $ varphi $ является непрерывно дифференцируемой и выполняется равенство $$ varphi^ (y) = frac <f^(x)> $$ для значений $ x $ и $ y $, связанных равенством $ y=f(x) $.

Конструктивных аналитических способов нахождения функции, обратной к заданной $ y=f(x) $ можно сказать, что и нет. Задача сводится к разрешению этого уравнения относительно $ x $. Однако уже для полиномиальных $ f(x) $ решение такого уравнения в «хороших» функциях, т.е. в радикалах, возможно, в общем случае, только для $ deg f ♦

В альтернативу интерполяции, можно поставить задачу об аппроксимации обратной функции с помощью степенных рядов. Составим формальный ряд $$ varphi(y)=B_0+B_1(y-y_0) + B_2(y-y_0)^2+ dots + B_k(y-y_0)^k+ dots $$ Для значения $ y_0 $ из теоремы получаем два коэффициента этого ряда $$ B_0=x_0, B_1= 1/f^ (x_0) , . $$ Как получить следующий коэффициент $ B_2 $? Заметим, что если бы у обратной функции существовала бы вторая производная, то $ B_2 $ был бы следующим коэффициентом ряда Тейлора: $$ B_2 = varphi^(y_0)/2 , . $$ Для получения выражения $ varphi^(y_0) $ продифференцируем по $ y $ тождество $ f(varphi(y)) equiv y $. Тождество останется справедливым $$ f^_x(varphi(y)) varphi^_y(y)equiv 1 , . $$ При подстановке сюда $ y=y_0 $ получаем уже известное нам равенство $ f^_x(x_0)varphi^_y(y_0)=1 $. Но если продифференцировать еще раз, то получим $$ f^_(varphi(y)) left(varphi^_y(y)right)^2+f^_x(varphi(y)) varphi^_(y)equiv 0 , . $$ При подстановке сюда $ y=y_0 $ получаем $$ varphi^_(y_0)=- frac<f^_(x_0)><[f^_x(x_0)]^3> $$ в дополнительном предположении, что вторая производная от $ f(x) $ существует. Вычисление остальных старших производных $ varphi(y) $ в точке $ y_0 $ производится аналогичным приемом — лишь бы только существовали эти производные для функции $ f(x) $. $$ varphi^_(y_0)= frac<3,[f^_(x_0)]^2- f^_x(x_0)f^_(x_0) ><[f^_x(x_0)]^5> , $$ $$ varphi^_(y_0)= $$ А для выведения общей формулы $ varphi^_(y_0) $ используется формула Фаа-ди-Бруно. При полиномиальной $ f(x) $ ряд Тейлора для обратной функции всегда может быть построен.

Пример. Для функции $ y=-x^3+3,x-1 $ приведенного выше примера первые $ 8 $ членов разложение обратной функции в ряд Тейлора в точке $ y_0=-1 $ имеют вид

$$ widehat(y)= frac(y+1)+frac(y+1)^3+frac(y+1)^5 +frac(y+1)^7 , . $$ На графике внизу кривая $ y = widehat(x)$ изображена цветом охры.

И только близко к точке $ x=1 $ заметно расхождение с $ y= varphi(x) $. ♦

Теорема утверждает, что обратная функция будет определена в окрестности точки $ y_0 $, удовлетворяющей условию. Насколько большой можно сделать эту окрестность? Ограничимся случаем полиномиальных $ f(x) $. При движении от точки $ y_0 $ вправо или влево по числовой оси значения $ varphi^(y) $ меняются непрерывным образом и стремятся к бесконечности только когда соответствующие значения $ x $ стремятся к корням полинома $ f^(x) $. Если этот полином имеет вещественные корни, и $ mu_1 непрерывные функции $ varphi(u,v) $ и $ psi(u,v) $ такие, что $$ f(varphi(u,v),psi(u,v)) equiv u, g(varphi(u,v),psi(u,v)) equiv v, varphi(u_0,v_0)=x_0, psi(u_0,v_0)=x_0 , . $$ Функции $ varphi $ и $ psi $ непрерывно дифференцируемы в этой окрестности, и для их матрицы Якоби выполняется равенство $$ left(begin partial varphi/ partial u & partial varphi/ partial v \ partial psi/ partial u & partial psi/ partial v end right)= left(begin partial f/ partial x & partial f/ partial y \ partial g/ partial x & partial g/ partial y end right)^ , . $$ Левая часть этого матричного равенства вычисляется в точках $ (u,v) $, соответствующих точкам $(x,y) $, в которых вычисляется правая часть (т.е. эти пары подчиняются равенствам $ u=f(x,y),v=g(x,y) $).

Отображение окрестности точки $ (u_0,v_0) $ в окрестность точки $ (x_0,y_0) $, заданное векторной функцией $ (varphi(u,v), psi(u,v)) $ из теоремы, называется обратным отображением к отображению $ (f(x,y),g(x,y)) $.

При выполнении условий теоремы, в соответствующих друг другу точках $ (u,v) $ и $ (x,y) $ выполняется равенство

Пример. Отображение

$$ (e^x cos y, e^x sin y > $$ отображает $ (x,y) $-плоскость $ mathbb R^2 $ во множество $ mathbb R^2 setminus (0,0) $ на плоскости $ (u,v) $. Якобиан $$ frac equiv e^ $$ отличен от нуля во всей плоскости $ (x,y) $. Можно было бы ожидать, что обратное отображение однозначно определено во всей области $ mathbb R^2 setminus (0,0) $. Но очевидно, что это не так: бесконечное множество $$ $$ отображается в точку $ (u,v)=(1,0) $. Обратное отображение бесконечнозначно. Результат теоремы справедлив если мы рассмотрим отображение любой полосы шириной $ 2 pi $ плоскости $(x,y) $, параллельной оси $ O x $. Например, полосы $ 0le y ♦

Мы в дальнейшем ограничимся случаем полиномиальных функций. Для этого случая хотя бы можно ожидать, что якобиан будет из того же класса, что и сами функции, т.е. полиномом. Ну и можно что-то конструктивное сказать о представлении обратных отображений — хотя они уже, как правило, не будут полиномиальными, но задачу их представления можно свести к одномерному случаю.

Пример. Найти обратное отображение к отображению

Решение. Якобиан $$ frac=left| begin -4,x+5,y-2 & 5,x-6,y+1 \ 2,x-2,y-1 & -2,x+2,y+1 end right|=-2,x^2+4,xy-2,y^2+3,x -3,y-1equiv $$ $$ equiv (-2x+2y+1)(x-y-1) , . $$ отличен от нуля во всех точках плоскости, за исключением лежащих на прямых $ y=x-1 $ и $ y=x-1/2 $. Согласно теореме, обратное отображение должно существовать, например, в окрестности точки $ (u,v)=(-5,7)=(f(-1,1),g(-1,1)) $.

Для разрешения системы алгебраических уравнений $ u=f(x,y), v=g(x,y) $ относительно $ x $ и $ y $ применим теорию исключения. Результант системы по переменной $ y $ $$ mathcal X(x)=(1-v)x^2+(u+11,v-9)x+u^2-6,u-34,v+9,v^2+6,uv+21 $$ оказывается квадратным полиномом 1) по $ x $. Корни уравнения $ mathcal X(x) =0$ следующие: $$ frac<u+11v-9pm (u+3v-1)sqrt> , . $$ Из них только соответствующий знаку минус в числителе, т.е. $$ varphi(u,v):=frac<u+11v-9 — (u+3v-1)sqrt> $$ удовлетворяет условию $ varphi(-5,7)=-1 $. Аналогично находим выражение для $ y $: $$ psi(u,v):=frac<u+10v-8 — (u+2v)sqrt> , . $$ Области определения обеих функций одинаковы: $$ , . $$ Теперь проверим справедливость формулы, связывающей якобианы. Имеем (в окрестности точки $ (-5,7) $) $$ frac= frac<2(1-v)sqrt>left[sqrt-1 right] , . $$ Подстановка сюда $ u=f(x,y), v= g(x,y) $ дает (в окрестности точки $ (1,-1) $) $$ frac equiv left( frac right)^ , . $$ ♦

Сформулируем обобщение предыдущего результата в $ mathbb R^n $.

Теорема. Если якобиан системы полиномов

$$ subset mathbb R[X] $$ отличен от нуля в некоторой точке $ X_0 in mathbb R^n $, то существует окрестность этой точки, в которой система уравнений $$ y_1=f_1(x_1,dots,x_n),dots,y_n=f_n(x_1,dots,x_n) , $$ рассматриваемая относительно переменных $ x_,dots,x_n $, имеет единственное решение, лежащее в окрестности точки $$ Y_0=(f_1(X_0), dots , f_n(X_0)) , . $$ Иными словами: существует и однохначно определяется система непрерывных в окрестности точки $ Y_0 $ функций $$ , $$ таких, что $$ f_1(varphi_1(Y),dots, varphi_n(Y))equiv y_1,dots, f_n(varphi_1(Y),dots, varphi_n(Y))equiv y_n $$ и $$ (varphi_1(Y_0),dots, varphi_n(Y_0))=X_0 , .$$ Функции $ _^n $ непрерывно дифференцируемы в указанной окрестности. Матрицы Якоби систем функций $ _^n$ и $ _^n$ связаны равенством: $$ left( begin / & / & dots & / \ dots & && dots \ / & / & dots & / end right)= left( begin / & / & dots & / \ dots & && dots \ / & / & dots & / end right)^ , . $$ Здесь производные в левых и правых частях равенства вычислены в соответствующих точках.

При выполнении условий теоремы, в соответствующих друг другу точках $ Y $ и $ X $ выполняется равенство

Якобиан как коэффициент растяжения

Еще одну важную сущность якобиана сформулируем в решении следующего примера.

Пример. Отображение

$$ left< begin u=f(x,y):=&-1/2,x^2-3/4,xy-y^2-x-1/2,y+2,\ v=g(x,y):=& 1/4,x^2-1/2,xy-1/2,y^2-x+1/2,y+1 end right. $$ отображает окрестность точки $ (x_0,y_0)=(0,1) $ в окрестность точки $ (u_0,v_0)=(1/2,1) $. Квадрат $ 0 le x le 1, 0 le y le 1$ отображается в область плоскости $ (u,v) $, органиченную параметрически заданными кривыми $$ , , $$ $$ , . $$ Как соотносятся между собой площади двух областей: исходного квадрата и его образа?

Решение. Для ответа на вопрос надо обладать возможностью вычислить точную площадь области, закрашенной оранжевым на рисунке. Я не уверен, что это можно сделать сведением к случаю «табличных» интегралов, но, по крайней мере, численными методами можно найти приближение этой площади. Попробуем получить такое приближение, заменив границу области — криволинейную — на параллелограмм. С этой целью проведем в точке $ (u_0,v_0) $ касательные к ограничивающую область кривым: $$ < (u,v)= (u_0+ f^_x(x_0,y_0) t, v_0+ g^_x(x_0,y_0) t) mid t in mathbb R > mbox < (u,v)=(u_0+ f^_y(x_0,y_0) tau, v_0+ g^_y(x_0,y_0) tau )mid tau in mathbb R > , . $$ и возьмем на них, помимо $ (u_0,v_0) $, точки, соответствующие значениям параметров $ t=1, tau=1 $.

Эта аппроксимация, в нашем конкретном случае, очевидно неудачная. Как следствие, площадь получишегося параллелограмма визуально отличается от искомой площади. Однако если уменьшить размеры отображаемого квадрата на плоскости $ (x,y) $ до $ 0 le x le 1/2, 1/2le y le 1 $, то его образ становится более похожим на параллелограмм построенный по приведенному выше образцу. В общем случае отображения квадрата размера $ delta times delta $ получаем приближение его образа в виде параллелограмма с вершинами $$ (u_0,v_0), (u_0+f^_x delta,v_0 +g^_x delta), (u_0+f^_y delta,v_0 +g^_y delta) , , $$ $$ (u_0+f^_x delta++f^_y delta,v_0 +g^_x delta+g^_y delta) , . $$ Здесь все производные вычислены в точке $ (x_0,y_0) $. Воспользовавшись формулой вычисления площади параллелограмма, получаем выражение в виде абсолютной величины (модуля) выражения $$ left|begin f^_x & g^_x \ f^_y & g^_y end right| delta^2 , . $$ Чем меньше $ delta $ тем меньше отклонение этого приближения от образа квадрата при отображении. Если изображать образы точек под воздействием отображения на той же исходной плоскости, то можно сказать, что абсолютная величина якобиана представляет собой коэффициент сжатия (или растяжения) бесконечно малой области вокруг точки, в которой он вычисляется. В настоящем примере $$ frac Bigg|_= — frac , $$ т.е. малая окрестность точки $ (0,1) $ «резиновой» плоскости сдвинется к точке $ (1,-1) $ и растянется примерно в четыре раза. ♦

Неявная функция

Обобщением рассмотренного в предыдущем пункте случая, т.е. выражения вектора $ X=(x_1,dots,x_n) $ через вектор $ Y=(y_1,dots,y_n) $ при задании многомерного отображения формулами $$ Y= (f_1(X),dots,f_n(X)) $$ является случай неявной функции.

В линейном случае, эта задача встречается при записи общего решения системы линейных уравнений. Если эта система представлена в виде $$ left< begin a_y_1 &+a_y_2&+ ldots&+a_y_n &+a_x_&+ldots & +a_x_ -b_1=0,\ a_y_1 &+a_y_2&+ ldots&+a_y_n &+a_x_&+ldots & +a_x_ -b_2=0,\ dots & & & & dots & dots & & dots \ a_y_1 &+a_y_2&+ ldots&+a_y_n &+a_x_&+ldots & +a_x_ -b_n=0 end right. $$ при $ mge 1 $, то при условии $$ left| begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right| ne 0 $$ ее можно разрешить относительно переменных $ y_1,dots,y_n $ — например, по формулам Крамера или посредством обратной матрицы: $$ left( begin y_ \ y_ \ vdots \ y_ end right) = — left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)^ left( begin a_ & dots & a_ \ a_ & dots & a_ \ dots && dots \ a_ & dots & a_ end right) left( begin x_ \ \ vdots \ x_ end right)+left( begin a_ & a_ & dots & a_ \ a_ & a_ & dots & a_ \ dots &&& dots \ a_ & a_ & dots & a_ end right)^ left( begin b_ \ \ vdots \ b_ end right) , . $$

В случае нелинейного уравнения $$ f(x,y)=0 , $$ критерий существования неявной функции дается следующей теоремой

Теорема 1 [о неявной функции]. Пусть функция $ f $ — непрерывно дифференцируема в окрестности точки $ (x_0,y_0) $ и

$$ f(x_0,y_0)=0 , partial f /partial y mid_ne 0 , .$$ Тогда существует окрестность точки $ x_0 $, в которой уравнение $ f(x,y)=0 $ имеет единственное вещественное решение относительно $ y $, лежащее в окрестности $ y_0 $. Иными словами: существует вещественная непрерывная функция $ varphi(x) $, такая, что $$ varphi(x_0)=y_0, f(x,varphi(x)) equiv 0 $$ (последнее тождество выполняется в заявленной окрестности $ x_0 $). При этом $ varphi(x) $ является непрерывно дифференцируемой функцией в той же окрестности и выполняется тождество $$ varphi^(x)equiv-frac Bigg|_<_> , . $$

Нахождение явного выражения для $ y=varphi(x) $ является задачей еще более сложной, чем задача предыдущего пункта о нахождении обратной функции. Усложнение проявляется уже в проблеме поиска хотя бы одной точки $ (x_0,y_0) in mathbb R^2 $, удовлетворяющей уравнению $ f(x,y)=0 $. Проблема существования вещественного решения этого уравнения даже для случая полиномиальной функции $ f $ нетривиальна: см. пункт ☞ АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ. Если вещественное решение удастся обнаружить, то нахождение неявной функции можно осуществить построением ряда Тейлора (или, в общем случае, при нарушении условия теоремы, в виде ряда Пюизё), сходящегося в некоторой окрестности точки $ x_0 $.

Результат теоремы $ 1 $ очевидным образом обобщается на случай неявной функции нескольких переменных: уравнение $$ f(x_1,dots,x_n, y) = 0 quad mbox n ge 2 $$ пытаются разрешить относительно $ y $.

Более общую задачу решения системы уравнений относительно нескольких переменных мы рассмотрим в частном случае уравнений алгебраических.

Теорема 2. Пусть имеется система полиномов

$$ subset mathbb R[X,Y], m ge 2 $$ от векторов переменных $ X=(x_1,dots,x_n) $ и $ Y=(y_1,dots,y_m) $. Пусть выполнены следующие условия:

$$ f_1(X_0,Y_0)=0, dots , f_m(X_0,Y_0)=0 , . $$

Рассмотрим сначала самый простой случай: $$ f(x,y,z)=0, g(x,y,z)=0 , . $$ Будем предполагать, что каждое из уравнений задает некоторую поверхность в $ mathbb R^3 $. Две неявно заданные алгебраические поверхности в $ mathbb R^3 $ могут не иметь вещественных точек пересечения. Как установить существование точек пересечения, т.е. наличие вещественных решений системы уравнений? Для полиномимальных $ f $ и $ g $ этот факт можно установить алгебраическими методами, которые проиллюстрирую на примере.

Пример. Пусть заданы две квадрики

$$ f(x,y,z):=frac9+frac-frac-1=0, $$ $$ g(x,y,z):= 111376, x^2-14656, xy+72128, xz+45184, y^2-45184, yz+76096, z^2+ $$ $$ +92136, x-118608, y+205104, z-1913751=0 $$ Первая является однополостным гиперболоидом, а вторая — эллипсоидом. Эти поверхности пересекаются по двум замкнутым кривым $ mathbf K_1 $ и $ mathbf K_2 $. На одной из них выбираем произвольную точку, например $$ (x_0,y_o,z_0) approx (1.959148, 3.864766, 3) , . $$

Отложив на несколько последующих абзацев ответ на вопрос, как эти координаты найдены, займемся задачей нахождения касательной к кривой $ mathbf K_1 $ в указанной точке.

Докажем, что в окрестности точки кривую $ mathbf K_1 $ можно представить параметрически $$ x=varphi_1 (z), y= varphi_2 (z), z= z , . $$ Действительно, матрица Якоби $$ mathbf J=left(begin 2/9 x & 1/6 y \ 222752, x-14656, y+72128, z + 92136 & -14656, x+90368, y-45184, z-118608 end right) $$ имеет ненулевой определитель в точке $ (x_0,y_o,z_0) $. В соответствии с теоремой 2, параметрическое представление кривой существует в некоторой окрестности точки $ z_0 $. Явное выражение для функций $ varphi_1, varphi_2 $ — отдельная нетривиальная проблема, но для поставленной конкретной задачи поиска касательной решение этой проблемы не требуется. Действительно, теорема 2 дает представление $$ (varphi_1^(z_0), varphi_2^(z_0),1) approx (-1.052314,1.445142,1) $$ для направляющего вектора касательной в виде явного выражения через значения функций $ f $ и $ g $ (и их производных) в точке $ (x_0,y_0,z_0) $.

А теперь проверим полученный результат альтернативным алгоритмом, задействовав технологию исключения переменных (которую мы уже использовали в предыдущем ПУНКТЕ). Cоставив результант полиномов $ f $ и $ g $ по переменной $ y $, придем к уравнению $$ F(x,z)=0 $$ при $$ F(x,z):=mathcal R_y(f,g)= $$ $$ =fracx^4+fracx^3z+fracx^2z^2+frac,xz^3+fracz^4+ $$ $$ +frac x^3+frac x^2 z+frac x z^2+frac z^3- $$ $$ -fracx^2-fracxz-fracz^2-fracx-fracz+frac , . $$ Имеем: $ deg_x F=4 $, т.е. уравнение $ F(x,z)=0 $ разрешимо в радикалах относительно $ x $. По крайней мере, теоретически, функцию $ varphi_1(z) $ можно представить в виде конечной комбинации элементарных функций и корней второй и третьей степеней от коэффициентов полинома. Реальное же представление для $ varphi_1(z) $ крайне громоздко и, с точки зрения практического использования, неконструктивно.

Уравнение четвертой степени может иметь от нуля до четырех вещественных корней в зависимости от значений $ z $. При подстановке конкретного значения $z =z_0 in mathbb R $ получаем полином $ F(x,z_0) $ от одной переменной $ x $. Мы можем однозначно и чисто алгебраическим алгоритмом установить число его вещественных корней. Так, $$ F(x,3)equiv fracx^4+126573205 x^3+fracx^2+fracx-frac $$ имеет два вещественных корня $ approx -3.309237 $ и $ approx 1.959148 $. Второй из них мы и взяли выше в качестве $ x_0 $. Таким образом, для $ varphi_1(z) $ мы получили представление в виде неявной функции $ F(x,z)=0 $ при заданном значении $ varphi_1(z_0)=x_0 $. Но тогда для этой функции должна работать теорема 1, которая дает представление $$ varphi_1^(z_0)= -frac Bigg|_<_> , . $$ Результат совпадает с полученным выше.

Понятно, что для получения $ varphi_2(z) $ мы должны произвести процедуру исключения переменной $ x $ из системы $ f=0,g=0 $, т.е. вычислить результант $ G(y,z):=mathcal R_x(f,g) $. Далее найти корень полинома $ G(y,z_0) $ (выбрав тот из них, что соответствует уже найденном у значению $ x_0 $) и т.д. Убеждаемся, что $$ varphi_2^(z_0)= -frac Bigg|_<_> , . $$

Вопроc: какая же связь между матрицей Якоби и результантами $ mathcal R_x(f,g), mathcal R_y(f,g) $ приводит — в результате применения двух различных алгоритмов — к совершенно разным представлениям для $ varphi_1^(z_0), varphi_2^(z_0) $, имеющим, тем не менее, одинаковые значения? ♦

Если система полиномов

$$ $$ удовлетворяет условиям теоремы в некоторой точке $ (X_0,Y_0) in mathbb R^ $, то существует окрестность точки $ X_0 $, в которой справедливо равенство $$ frac=(-1)^n frac bigg/ frac , . $$ Здесь производные вычислены в соответствующих точках.

Геометрические приложения

Теорема. Пусть на плоскости заданы две кривые уравнениями

$$ f(x,y)=0 quad u quad g(x,y)=0 $$ и они пересекаются в точке $ (x_,y_0) $. Тогда величина угла $ gamma $, под которым происходит это пересечение вычисляется по формуле $$ operatorname (gamma) = pm frac<frac frac — frac frac><frac frac + fracfrac> $$ где все производные в правой части вычислены в точке $ (x_,y_0) $.

Утверждение следует из свойства градиента: вычисленный в точке кривой, он определяет направляющий вектор нормали к этой кривой.

Если $ (x_,y_0) $ — точка пересечения кривых $ f(x,y)=0 $ и $ g(x,y)=0 $, то

Показать, что если функции $ u_(x,y) $ и $ v_(x,y) $ связаны соотношениями Коши-Римана (Даламбера-Эйлера):

$$ frac equiv frac , frac equiv — frac $$ в некоторой области $ mathbb_ $, то в этой области их линии уровня, то есть кривые $ u(x,y) = c_1 $ и $ v(x,y) = c_2 $ при $ subset mathbb R $, могут пересекаться только под прямым углом.

Решение системы нелинейных уравнений

Рассмотрим систему двух вещественных алгебраических уравнений $$ f(x,y)=0, g(x,y)=0 , . $$ По аналогии с методом Ньютона решения уравнения от одной неизвестной, попробуем найти вещественное решение этой системы, сгенерировав итерационную последовательность в $ mathbb R^2 $, сходящуюся к этому решению. Допустим, что из каких-то соображений нам удалось установить, что вещественное решение системы существует, и что некоторая точка $ (x_0, y_0) $ достаточно близка к этому решению. Раскладываем полиномы по формуле Тейлора по степеням $ x-x_0, y-y_0 $ и оставляем в этих разложениях только первые слагаемые: $$ f(x,y)equiv f(x_0,y_0)+ fracBigg|_(x-x_0)+fracBigg|_(y-y_0) + dots , , $$ $$ g(x,y)equiv g(x_0,y_0)+ fracBigg|_(x-x_0)+fracBigg|_(y-y_0) + dots , . $$ Теперь вместо системы нелинейных уравнений рассматриваем систему $$ left< begin f(x_0,y_0)&+ fracBigg|_(x-x_0)+fracBigg|_(y-y_0) &= 0,\ g(x_0,y_0)&+ fracBigg|_(x-x_0)+fracBigg|_(y-y_0) &= 0 end right. $$ линейных уравнений. Она гарантировано имеет решение если матрица $$ mathbf J= left( begin partial f /partial x & partial f /partial y \ partial g /partial x & partial g /partial y end right) $$ будет неособенной при $ x=x_0,y=y_0 $. При этом предположении решение системы единственно и может быть выражено в виде $$ left( begin x_1 \ y_1 end right)= left( begin x_0 \ y_0 end right) — mathbf J^ left( begin f(x_0,y_0) \ g(x_0,y_0) end right) , . $$ Получаем полную аналогию с одномерным методом Ньютона; роль производной теперь выполняет матрица Якоби. Можно ожидать, что точка $ (x_1,y_1) $ будет лежать ближе к неизвестному нам решению исходной системы, нежели стартовая точка $ (x_0, y_0 ) $. Если это предположение выполняется, то можно попытаться организовать вычисление итерационной последовательности $$ left< left( begin x_j \ y_j end right)= left( begin x_ \ y_ end right) — mathbf J^ Bigg|_<_<(x_,y_)>> left( begin f(x_,y_) \ g(x_,y_) end right) right>_^ $$ и потестировать ее на сходимость к решению. Одно ограничение для этого умозаключения довольно очевидно: матрица Якоби должна быть невырожденной на всех итерациях (а, желательно, и не очень близкой к вырожденным матрицам).

Подробнее о методе Ньютона решения систем нелинейных уравнений ☞ ЗДЕСЬ.

🎥 Видео