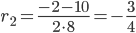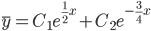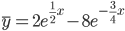Уравнение y 2y 3y 0 является

Дифференциальным уравнением называется уравнение которое связывает неизвестную функцию и её производные различных порядков:

F ( x , y ‘ , y » , . , y ( n ) ) = 0

Порядком дифференциального уравнения называется порядок его старшей производной. Решить дифференциальное уравнение, значит найти неизвестную функцию , которая обращает это уравнение в верное тождество. Этого можно достичь, изучив теоретический материал по дифференциальным уравнениям, или воспользовавшись нашим онлайн калькулятором.

Наш калькулятор может находить как общее решение дифференциального уравнения, так и частное. Для поиска частного решения, необходимо ввести начальные условия в калькулятор. Для поиска общего решения, поле ввода начальных условий необходимо оставить пустым.

Видео:Решение однородного дифференциального уравнения второго порядка yʹʹ + 2yʹ − 3y = 0Скачать

Решение линейных дифференциальных уравнений

Пример 1 . Общее решение дифференциального уравнения с правой частью: y» + py’ + qy = R(x) получается с помощью квадратур из общего решения соответствующего уравнения без правой части y» + py’ + qy = 0 где R(x) = e αx [P₁(x)cos(βx) + P₂sin(βx)]

1. Для уравнения y»’ — 4y» + 5y’ – 2y = 2x+3 корнями характеристического уравнения r 3 – 4r 2 + 5r – 2 = 0 являются r=2 кратности 1 и r=1 кратности 2. Следовательно α+β i=0 и не является корнем характеристического уравнения. Поэтому k=0 и частное решение ищем в виде y = cx + d. Так как y’ = 0, y’’ = 0, y’’’ = 0, то, подставляя в уравнение, получаем 5c — 2cx — 2d = 2x + 3. Приравнивая коэффициенты при одинаковых степенях x, получаем -2c = 2. -5c – 2d = 3. Следовательно, c=-1, d= -4 и y = -x-4 — частное, а y = -x-4+C₁e x + C₂e 2 x — общее решения уравнения.

2. Для уравнения y»’ — 4y» + 5y’ – 2y = (2x+3)e 2 x число α+β i=2 является корнем характеристического уравнения кратности 1. Поэтому частное решение ищем в виде y = x(cx + d)e 2 x .

3. Для уравнения y’’ + y = cos(x) корнями характеристического полинома r 2 +1 являются числа r = ±i кратности 1. Поэтому частное решение ищем в виде y=x(a₁cosx + a₂ sinx). Тогда
y’ = (a₁ + a₂x)cosx + (a₂ – a₁x)sinx,
y’’ = (2a₂ – a₁x)cosx + (-2a₁-a₂x)sinx
Подставляя в исходное уравнение и приводя подобные, получаем 2a₂ cosx – 2a₁sinx = cosx, откуда a₁ = 0;a₂=0,5.

4. Найти общее решение уравнения: y» — 3y’ + 2y = x 2 + 3x
Находим решение однородного уравнения y» — 3y’ + 2y = 0.
Характеристическое уравнение: r 2 -3r+2=0 имеет корни r₁= 1, r₂= 2.
Общее решение уравнения без правой части равно: y_Общ = C₁e x + C₂e 2x
Правая часть уравнения имеет вид R(x) = P(x)e αx , причем P(x) = x 2 + 3x и число α = 0 не является корнем характеристического уравнения. Ищем решение вида: y * = Ax 2 + Bx + C Находим y»,y’, которые подставляем в равенство:
2Ax 2 + (2B — 6A)x + 2C — 3B + 2A = x 2 + 3x
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
2A = 1; 2B — 6A = 3; 2C — 3B + 2A = 0,
из которых находим: A = 1/2, B = 3, C = 4, так что
y * = x 2 /2 + 3x + 4
Общее решение дифференциального уравнения есть: y = y_Общ + y * = C₁e x + C₂e 2x + x 2 /2 + 3x + 4

5. Найти общее решение уравнения: y» — 3y’ = x 2 + 3x
Характеристическое уравнение: r 2 — 3r = 0 имеет корни r₁= 3, r₂= 0.
Общее решение уравнения без правой части равно: y_Общ = C₁e 3x + C₂e 0 = C₁e 3x + C₂ Правая часть уравнения имеет вид R(x) = P(x)e αx , причем P(x) = x 2 + 3x и число α = 0 является однократным корнем характеристического уравнения. Ищем решение вида: y * = x(Ax 2 + Bx + C) Находим y»,y’, которые подставляем в равенство y» — 3y’ = x 2 + 3x.
Приравнивая коэффициенты при одинаковых степенях х, получаем систему:
-9A = 1, -6B + 6A = 3, -3C + 2B = 0,
из которых находим: A = -1/9, B = -11/18, C = -11/27, так что
y * = x 2 /9 — 11x/18 -11/27
Общее решение дифференциального уравнения есть: y = y_Общ + y * = C₁e 3x + C₂ + x 2 /9 — 11x/18 -11/27

Пример 2 . Решить дифференциальное уравнение 8y» +2y’ — 3y = 0.
Решение. Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
8r 2 +2r — 3 = 0
D = 2 2 — 4·8·(-3) = 100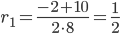
,
Корни характеристического уравнения: r₁ = 1 /₂, r₂ = -3 /₄
Следовательно, фундаментальную систему решений составляют функции: y₁ = e 1/ 2x , y₂ = e -3/ 4x
Общее решение однородного уравнения имеет вид:
Найдем частное решение при условии: y(0) = -6, y'(0) = 7
Поскольку y(0) = c₁+c₂, то получаем первое уравнение:
c₁+c₂ = -6
Находим первую производную:
y’ = 1 /₂•c₁•e 1/ 2•x — 3 /₄•c₂•e -3/ 4•x
Поскольку y'(0) = 1 /₂•c₁— 3 /₄•c₂, то получаем второе уравнение:
1 /₂•c₁— 3 /₄•c₂ = 7
В итоге получаем систему из двух уравнений:
c₁+c₂ = -6
1 /₂•c₁— 3 /₄•c₂ = 7
которую решаем или методом матриц или методом исключения переменных.
c₁ = 2, c₂ = -8
Тогда частное решение при заданных начальных условиях можно записать в виде:

Видео:#2.76 y''-2y'-3y=0 [General Solution, Differential Equation]#Demidovich, #ДемидовичСкачать

Дифференциальные уравнения по-шагам

Видео:y"-2y'-3y=0 (IVP)initial value problem solved exercise problem from Earl A CoddingtonСкачать

Результат

Примеры дифференциальных уравнений

• Простейшие дифференциальные ур-ния 1-порядка
• Дифференциальные ур-ния с разделяющимися переменными
• Линейные неоднородные дифференциальные ур-ния 1-го порядка
• Линейные однородные дифференциальные ур-ния 2-го порядка
• Уравнения в полных дифференциалах
• Решение дифференциального уравнения заменой
• Смена y(x) на x в уравнении
• Другие

Указанные выше примеры содержат также:

• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс actan(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  asinh(x), acosh(x), atanh(x), actanh(x)
• число Пи pi
• комплексное число i

Правила ввода

Можно делать следующие операции

2*x — умножение 3/x — деление x^3 — возведение в степень x + 7 — сложение x — 6 — вычитание Действительные числа вводить в виде 7.5, не 7,5

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

📺 Видео

Solve differential equation y’’-2y’-3y=0 using Laplace transform.Скачать

Частное решение однородного дифференциального уравнения второго порядка y′′−3y′+2y=0, y(0)=2 y′(0)=2Скачать

Решение однородного дифференциального уравнения второго порядка y′′ − 3y′ = 0Скачать

Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

#2.122 y''''+4y''+3y=0 [Differential Equation, General Solution]Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

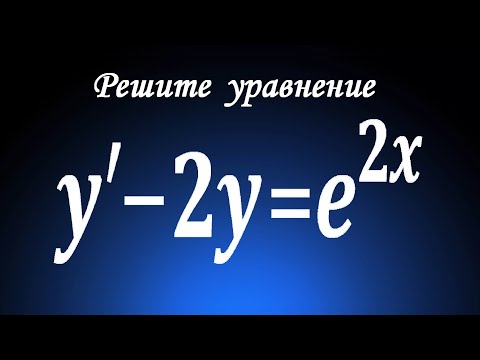
18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

#Дифуры I. Урок 6. Уравнения в полных дифференциалах (УПД)Скачать

finding the general solution of 5y''-2y'-3y=0 - math is hot!Скачать

#2992 y''+3y'=0 [Demidovich]Скачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Частное решение однородного дифференциального уравнения второго порядка y′′−2y′=0, y(0)=1, y′(0)=1Скачать

12.4. Решить систему уравнений: x^2-y^2+3y=0, x^2+3xy+2y^2+2x+4y=0. В.В.ТКАЧУК МАТ-КА АБИТУРИЕНТУ.Скачать

#2.129 y''''''-2y'''''+3y''''-4y'''+3y''-2y'+y=0 [Differential Equation]Скачать

#Дифуры II. Урок 5. Уравнение ЭйлераСкачать