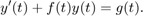Уравнение ван дер поля матлаб

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Уравнение ван дер поля матлаб

3 -е занятие по MATLAB

ЛАБОРАТОРНАЯ РАБОТА №3

Трехмерная графика в MATLAB .

Решение обыкновенных дифференциальных уравнений в MATLAB .

1. Элементарная трехмерная (3- D ) графика — функция plot 3.

Функция plot 3 в определенном смысле является аналогом функции plot . С помощью plot 3 формируется построение линии в трехмерном пространстве по заданным трем векторам .

Пример 1.1. Построение трехмерной пространственной спирали.

t =0:0.05:9* pi ; x =2* sin ( t ); y = cos ( t ); % t , x , y — вектора одинакового размера

xlabel( ‘о сь X’ ),ylabel( ‘ось Y’ ),zlabel( ‘ось Z-t’ )

title(‘ Пространственная спираль ‘)

% Сохранить программу в текстовом редакторе MATLAB, например, под именем sp3

% Поменять местами x, y, t в функции plot3

% Сменить начертание и цвет графика

% Добавить пояснение к начертанию в виде легенды — legend( ‘ звездочки ‘ )

%Установить следующий диапазон для t: t=-9*pi:0.05:9*pi;

% Пояснения к графику с помощью функций gtext для 3D-графики не применяются

Пример 1.2. Построение сферы по окружностям.

n=input(‘n=’); % Клавиатурный ввод числа n по запросу в командном окне

t2=(pi/2)*(-n:5:n)’/n ; % транспонированный вектор

E=ones(size(t1)); % матрица единиц размерности вектора t1

% Сохранить программу в текстовом редакторе MATLAB под именем sfera3 .

% Программу выполнить при различных значениях n .

% При n =100 изменить шаг в массивах t1 и t2 : для t1 и t2 одновременно: 3, 1, 10, 25, 50

% Для t1=50, для t2=1; для t1=1, для t2=50.

% Программу sfera3 выполнить без клавиатурного ввода, а для заданного числа n .

% Установить в программе различные цвета изображения сферы.

% Использовать различные коэффициенты для t1 и t2: pi/5, pi/10, pi/50, 2*pi, 5*pi одновременно

% и в сочетании с коэффициентом, равным pi (3.14), при одном из векторов ( t1 или t2).

2. Формирование прямоугольной сетки на плоскости — meshgrid .

% Результатом действия функции meshgrid является формирование «основания» в плоскости XOY для построения над этим основанием пространственной фигуры.

3. Построение пространственных сетчатых фигур — mesh.

Z = 1*x.* exp(-x.^2 — y.^2); % Коэффициент 1 заменить: 2, 5, 10, 20

% Для сравнения применить plot3(x,y,Z),grid вместо mesh(Z) .

R=sqrt(x.^2+y.^2)+0.001; %Коэфф. 0.001 введен для исключения деления на ноль

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Для сравнения применить plot3(x,y,Z),grid

4. Сетчатая поверхность с проекциями линий постоянного уровня — meshс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

5. Сетчатая поверхность с пьедесталом плоскости отсчета на нулевом уровне— meshz.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

6. Построение пространственных сплошных фигур — surf.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

1. С плошная поверхность с проекциями линий постоянного уровня — surfс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

8. Стандартные сферические поверхности — sphere .

8 .1. Сфера единичного радиуса — sphere ;

» sphere % равносильно sphere(20);

8.2 Формирование сферы с произвольным радиусом, например, равным 5;

% Выполнить построения с надписями

9. Пространственное распределение вероятностей Гаусса — peaks.

peaks; % По умолчанию формируются матрицы размера 49 ´ 49, по которым строится

%поверхность с пометками координат и титульной надписью ‘Peaks’.

peaks, title(‘Gauss’); % Со специальной титульной надписью

peaks(78); % Размерность матриц построения 78 ´ 78

peaks(25); % Размерность матриц построения 25 ´ 25

z=peaks; surf(z); % Построение поверхности Гаусса по заданной 49 ´ 49 матрице z.

% Сравнить с поверхностью на основе функции mesh(z)

% Сравнить с функцией mesh(z)

z=3*peaks(78); surf(z), title(‘Gauss’) % С множителем по оси Z .

% Применить множители: 4, 10, 33, 50

Пример 9.3. Цветовые массивные уровни на плоскости от распределения Гаусса.

[X,Y,Z]=peaks; pcolor(7*X,12*Y,20*Z),title(‘Цвет’) % С расширенной %областью определения на плоскости XOY — множители 7 и 12 и с изменением по Z — коэф-

Пример 9.4. Распределение Гаусса с задаваемой областью определения на плоскости XOY.

% Функция pcolor позволяет наблюдать обл а сть определения в плоскости XOY

% Изменить шаг по x и y : 0.2, 0.1, 0.5

% Изменить границы по x и y одновременно и порознь :(-7:0.2:3),(-7:0.2:1),(-7:0.2:-1),(-7:0.2:-3)

Пример 9.5. Линии уровня трехмерной поверхности — contour.

% Линии уровня без учета масштаба плоскости XOY:

contour(peaks),grid,title(‘ Линии уровня ‘) % 10 линий уровня по умолчанию

contour(peaks,4),grid,title(‘ Линии уровня ‘) % 4 линии уровня

contour(peaks,10),grid,title(‘ Линии уровня ‘) % 10 лини q уровня

contour(peaks,15),grid,title(‘ Линии уровня ‘) % 15 лини q уровня

contour(peaks,25),grid,title(‘ Линии уровня ‘) % 25 лини q уровня

% Применить функцию contour для стандартной сферической поверхности sphere с различным числом линий уровня.

Пример 9.6. Линии уровня с учетом масштаба плоскости XOY (два примера):

Пример 9.7. Линии уровня с учетом масштаба плоскости XOY и заданным числом (три примера):

Пример 9.7. Линии уровня с цветовой окраской плоскости XOY — contourF.

contourF(peaks),title(‘Цвет линий уровня’)

Пример 9.8. «Пространственные» линии уровня — contour3.

contour3(peaks,25),title(’25 л иний уровня в пространстве ‘)

Пример 9.9. Обзор поверхности из заданной точки пространства — view.

peaks,view(10,45); % Число 10 — азимут обзора, 45 — угол обзора (все в градусах)

[X,Y]=meshgrid(-7:0.3:7,-5:0.3:5);Z=peaks(X,Y);surf(Z), view( — 10,45)

% Задать различные параметры функции view и выполнить построение различных поверхностей.

10. Пострение поверхностей относительно полярной системы координат.

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘)

% С изменением точки обзора

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘),view(-12,45)

11. Построение цилиндрических поверхностей — cylinder.

cylinder % Построение цилиндра без параметров, по умолчанию

cylinder(40) % Построение цилиндра с заданным размером плоскости XOY

cylinder(40,60) % Цилиндр с заданным размером плоскости XOY и числом образующих %граней — 60

% Построение совокупности цилиндрообразующих поверхностей

[x,y,z]=cylinder([5 0],160); surf(x,y,z) % Конус по заданному вектору [5,0]

[x,y,z]=cylinder([5 0 5],160); surf(x,y,z) % 2 к онуса

[x,y,z]=cylinder([5 0],3); surf(x,y,z) % Пирамида

[x,y,z]=cylinder([5 0 5],3); surf(x,y,z) % 2 пиирамиды

[x,y,z]=cylinder([5 12 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5 12 5 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 18],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,z)

% Построение совокупности цилиндрообразующих поверхностей с масштабированием

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,20*z)

plot(x,20*z),grid % Масштаб плоскости XOZ

plot(7*x,y),grid % Масштаб плоскости XOY

plot(7*x,13*y),grid % Масштаб плоскости XOY

Решение обыкновенных дифференциальных уравнений в MATLAB.

Для решения обыкновенных дифференциальных уравнений (ODE) могут быть применены численные методы, которые в MATLAB реализованы в специальных функциях-решателях: ode45, ode23, ode113 .

Общий порядок программирования:

1) Создается М-функция с описанием правых частей дифференциальных уравнений;

2) Создается М-сценарий с выбранным решателем;

Пример 1. Решить следующую систему обыкновенных дифференциальных уравнений с заданными начальными условиями:

% Программа решения примера 1

% Создаем М-функцию под именем dif31.m

% Создаем М-сценарий под именем ddd45_31.m

% Сценарий решения с помощью ode45

T=[0 15]; % Интервал интегрирования

x0=[10;5]; % Начальные условия

[t,x]=ode45(‘dif31’,T,x0); %t, x — выходные переменные решателя ode45

plot(t,x),grid,title(‘ Пример 3.1 ‘),legend(‘X1′,’X2’)

% Изменить начальные условия:

% Изменить интервал интегрирования: от 0 до 20, от 0 до 7.

% Вывести графические результаты с различным начертанием координат

% Прменить решатели ode23, ode113 . Сравнить результаты покоординатно, для чего вывести результаты решения и свести их в таблицу, например, в WORD .

Пример 2. Решить следующую систему линейных дифференциальных уравнений с заданными начальными условиями:

% Создаем М-функцию с именем dif32.m

function f=dif32(t,x); % t, x — входные переменные для М-функции

%Создаем М-сценарий под именем ddd45_32

% Сценарий решения примера 2

x0=[0;0;0]; % x0 — вектор начальных условий

% Изменить интервал интегрирования

% Изменить начальные условия

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 3. Уравнение Ван-дер-Поля.

Для решения дифференциального уравнения 2-го порядка сначала приведем его к системе дифференциальных уравнений 1-го порядка:

где

% Создаем М-функцию под именем van33.m

%Создаем М-сценарий под именем ddd45_33

plot(t,X),grid,title(‘ Ур-е Ван-дер-Поля ‘ ), legend(‘X1′,’X2’)

% Изменить интервал интегрирования

% Изменить начальные условия ( только все нулевые не должны быть)

% Изменить множитель в уравнении (вместо 2)

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 4. Интегрирование дифференциальных уравнений с выводом результатов в заданн ом диапазоне точек независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 4

T=[0:1:6,7:2:18]; % от 0 до 6 шаг 1, от 7 до 18 шаг 2

Пример 5. Интегрирование дифференциальных уравнений с выводом результатов в заданных точках независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 5

T=[0 0.5 1 1.5 3 4 8]; 7 точек переменного t

Задание к примерам 1-5: произвести графический вывод координат каждой в отдельности

Пример 6. Интегрирование систем линейных дифференциальных уравнений в матричном виде, т.е.

(6.1)

где — вектор переменных состояния размера n ´ 1, — вектор входного воздействия размера rx1, — матрицы чисел размера n ´ n, n ´ r, соответственно .

% Матрицы и берем из примера 2

% Создаем М-функцию под именем syst36.m

A=[-3,0,0;1,-2,0;0,4,-1]; % Матрица А размера 3 ´ 3

B=[10 0 0;0 0 0;0 0 0]; % Матрица B размера 3 ´ 3

u=[1;1;1]; % Входное воздействие размера 3 ´ 1

ds36=A*x+B*u; % Описание правой части матричного дифференциального уравнения (6.1)

% Создаем М-сценарий под именем ddd45_36

% Сценарий решения примера 3.6

plot(t,x),grid,title(‘ Система ур-й 3-го порядка ‘),

Задание к примеру 6:

% Решить систему с двумя воздействиями, с одним воздействием

% Вывести графические результаты с различным начертанием координат

% Вывести графические результаты с по отдельным координатам

% Создать программу решения системы дифференциальных уравнений 4-го порядка

% Использовать решатели ode23, ode113 .

Решение обыкновенных дифференциальных уравнений

с заданной точностью и с параметрами.

Решатели дифференциальных уравнений по умолчанию производят численное интегрирование с относительной погрешностью и вектором абсолютной погрешности со значением по всем компонентам вектора.

1. Установление заданной относительной погрешности RelTol — ODESET( odeset) .

С помощью установления относительной погрешности RelTol контролируется количество «правильных» цифр в решении дифференциального уравнения в соответствии с общей записью , где показатель степени P есть число контролируемых цифр в решении.

Пример1. Уравнение Ван-дер-Поля с заданной относительной погрешностью.

С помощью функции ODESET задаются опции решателя дифуравнений с помощью соответствующих строковых символов, которых всего может быть 18. Перечень строковых символов функции ODESET можно просмотреть из командной строки, набрав в ней ODESET

% Сформируем М-функцию для описания правых частей дифференциальных уравнений

% Сохрани ть под именем van33

% Создадим М-сценарий решения на основе ode23 и с относительной погрешностью, равной

% d1= 0.1 и d2=0.0001

% М-сценарий сохранить под именем ret71.

% Формат записи функции odeset включает строковый служебный символ RelTol и задаваемую %величину относительной погрешности (0.1 для d1 и 0.2 для d2).

% d1 и d2 подставляются в соответствующие решатели ( ode23).

Задание к примеру 1:

— выполнить с ode45, ode113;

— изменить коэффициент в М-функции van33 : 0.3, 2.3;

— изменить для d1 относительную погрешность: 1, 0.5, 0.1, 0.01, 0.001, 0.0001 (для ode23).

Пример 2. Анализ нелинейной тест-системы с задаваемой относительной погрешностью вычислений в решателях MATLAB.

где — постоянные действительные числа.

2.1. Проинтегрируем тест-систему с коэффициентами и с относительной погрешностью, равной 0.1, 0.01, 0.001, 0.4, 0.3, 0.2

% Создадим М-функцию под именем dif21

% Создадим М-сценарий под именем syst21

% Введем относительную погрешность 0.1

% В сценарии применим функцию odeset

% Проанализировать тест-систему по 2-й и 3-й координатам.

% Для графического вывода результатов по 2-й координате следует ввести plot в виде

%% Для графического вывода результатов по 3-й координате следует ввести plot в виде

% Проанализировать тест-систему с относительной погрешностью, равной 0.01, 0.4, 0.3, 0.2

% Проанализировать тест-систему с помощью решателей ode45, ode113 , сравнить результаты.

2. Задание абсолютной погрешности — AbsTol .

Абсолютная погрешность AbsTol контролирует разницу между ожидаемым решением и его действительным значением. AbsTol начинает проявляться, когда компонента (координата) решения становится неожидаемо большой. Влияние AbsTol зависит также от интервала и масштаба интегрирования. По умолчанию решатели дифференциальных уравнений Matlab устанавливают величину абсолютной погрешности, равную .

Пример3. Уравнение Ван-дер-Поля с заданной абсолютной погрешностью — ‘AbsTol’ .

% Используем имеющую М-функцию описания уравнения Ван-дер-Поля — van33

% Создадим М-сценарий ( присвоить имя) с задаваемой абсолютной погрешностью по всем координатам и по %одной из возможных

a1=odeset(‘AbsTol’,0.5); % Скаляр 0.1 по всем координатам

% Задание избирательной абсолютной погрешности осуществляется с помощью вектора в виде :

% По первой координате погрешность равна 0.5, по 2-й — 0.000001

% В целом сценарий (присвоить имя) должен иметь вид

% Поскольку система уравнений Ван-дер-Поля имеет взаимозависимые координаты, то интегрирование осуществляется практически с наименьшей погрешностью, т.е. с 0.000001

Задание к примеру 3.

— Применить скаляр абсолютной погрешности: 0.3, 0.1, 0.01.

— Вывести график по 2-й координате.

3. Интегрирование дифференциальных уравнений с параметрами.

Пример 4. Проинтегрировать однородную систему нелинейных дифференциальных уравнений с четырьмя параметрами k1, k2, k3, a:

при следующих начальных условиях:

Целью является анализ решений при различных параметрах, входящих в систему.

% Создадим М-функцию под именем dif44 с ключевым словом flag

switch flag % Начало процедуры описания правых частей дифуравнений

case » % Состояние flag с опциями по умолчанию

end % Окончание описания правых частей дифуравнений с опциями по умолчанию

% Создадим М-сценарий под именем syst44 для решателя ode23 c опциями по умолчанию

% и введения параметров

x0=[0;1;-1]; % Вектор начальных условий

tt=[0,25]; % Интервал интегрирования

k1=input(‘k1=’)%2.333; % Можно также k1=2.333;

k2=input(‘k2=’)%-0.7789; % Можно также k2=-0.7789;

k3=input(‘k3=’)%-0.7888; % Можно также k3=-0.7888;

a=input(‘a=’)%-0.1; % Можно также a=-0.1;

plot(t,x),grid,title(‘ Система с параметрами ‘), legend( ‘x1’ , ‘x2’ , ‘x3’ )

% В записи функции ode23 символ [ ] указывает на опции ( RelTol, AbsTol и др.), принятые по %умолчанию

Задание к примеру 4.

— Изменить параметр k1: 2, 1, 0.5, 0.2; ( остальные исходные) ;

— Изменить параметр k2: -0.111, -0.333,-0.555,0.7789 ( остальные исходные) ;

— Изменить параметр k3: -1.333, -0.333, -0.666, 0.7888 ( остальные исходные) ;

— Изменить параметр a: -1, 1, 0, 0.5 ( остальные исходные) ;

Произвести интегрирование системы при:

Пример 5. Интегрирование систем с циклическим изменением параметра.

% Используем М-функцию dif55

% Видоизменим М-сценарий syst66 так, чтобы программно изменялся какой-либо параметр (например, k3) и происходило наложение графиков решения по заданной координате (например, по ). Новый М-сценарий будет с именем syst77.

if i==-0.51 % Двойное равенство соответствует логической истине

plot(t,x(:,2),’r’),title(‘ Система с циклическим параметром ‘ )

k3=i; % Без точки с запятой (;) выводятся значения k3

Задание к примеру 5.

— Расширить диапазон изменения параметра k3;

— Написать программу с изменением параметра k2 ;

— Написать программу с графическим выводом всех координат системы при k3=0.51 и только координаты при остальных значениях параметра k3 .

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

ode45

Solve nonstiff differential equations — medium order method

Видео:Van der Pol Equation -Various Initial Conditions- [gnuplot]Скачать

Syntax

Видео:Lecture 5.3. Implementation of van der Pol's EquationСкачать

Description

[ t , y ] = ode45( odefun , tspan , y0 ) , where tspan = [t0 tf] , integrates the system of differential equations y ‘ = f ( t , y ) from t0 to tf with initial conditions y0 . Each row in the solution array y corresponds to a value returned in column vector t .

All MATLAB ® ODE solvers can solve systems of equations of the form y ‘ = f ( t , y ) , or problems that involve a mass matrix, M ( t , y ) y ‘ = f ( t , y ) . The solvers all use similar syntaxes. The ode23s solver only can solve problems with a mass matrix if the mass matrix is constant. ode15s and ode23t can solve problems with a mass matrix that is singular, known as differential-algebraic equations (DAEs). Specify the mass matrix using the Mass option of odeset .

ode45 is a versatile ODE solver and is the first solver you should try for most problems. However, if the problem is stiff or requires high accuracy, then there are other ODE solvers that might be better suited to the problem. See Choose an ODE Solver for more information.

[ t , y ] = ode45( odefun , tspan , y0 , options ) also uses the integration settings defined by options , which is an argument created using the odeset function. For example, use the AbsTol and RelTol options to specify absolute and relative error tolerances, or the Mass option to provide a mass matrix.

[ t , y , te , ye , ie ] = ode45( odefun , tspan , y0 , options ) additionally finds where functions of ( t, y) , called event functions, are zero. In the output, te is the time of the event, ye is the solution at the time of the event, and ie is the index of the triggered event.

For each event function, specify whether the integration is to terminate at a zero and whether the direction of the zero crossing matters. Do this by setting the ‘Events’ property to a function, such as myEventFcn or @myEventFcn , and creating a corresponding function: [ value , isterminal , direction ] = myEventFcn ( t , y ). For more information, see ODE Event Location.

sol = ode45( ___ ) returns a structure that you can use with deval to evaluate the solution at any point on the interval [t0 tf] . You can use any of the input argument combinations in previous syntaxes.

Видео:Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Examples

ODE with Single Solution Component

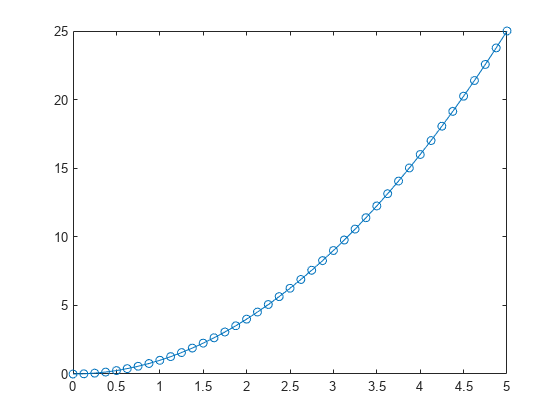
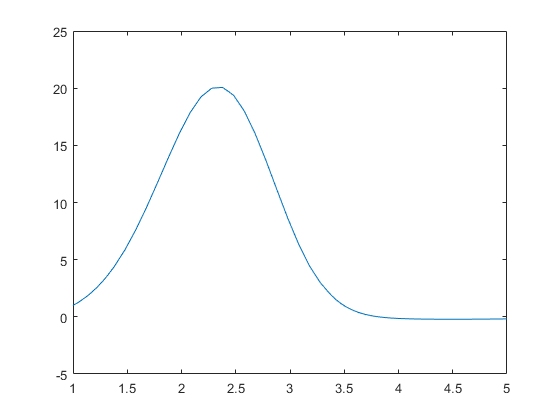
Simple ODEs that have a single solution component can be specified as an anonymous function in the call to the solver. The anonymous function must accept two inputs (t,y) , even if one of the inputs is not used in the function.

Specify a time interval of [0 5] and the initial condition y0 = 0 .

Plot the solution.

Solve Nonstiff Equation

The van der Pol equation is a second-order ODE

y 1 ′ ′ — μ ( 1 — y 1 2 ) y 1 ′ + y 1 = 0 ,

where μ > 0 is a scalar parameter. Rewrite this equation as a system of first-order ODEs by making the substitution y 1 ′ = y 2 . The resulting system of first-order ODEs is

y 1 ′ = y 2 y 2 ′ = μ ( 1 — y 1 2 ) y 2 — y 1 .

The function file vdp1.m represents the van der Pol equation using μ = 1 . The variables y 1 and y 2 are the entries y(1) and y(2) of a two-element vector dydt .

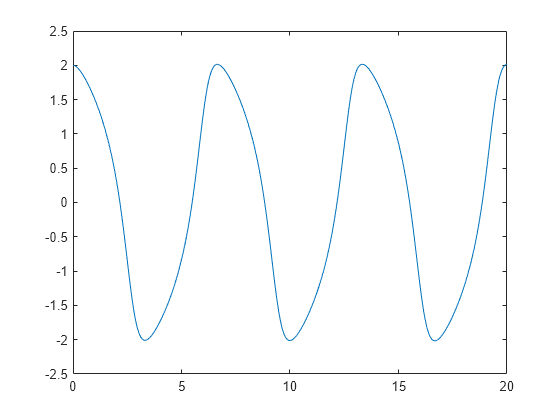
Solve the ODE using the ode45 function on the time interval [0 20] with initial values [2 0] . The resulting output is a column vector of time points t and a solution array y . Each row in y corresponds to a time returned in the corresponding row of t . The first column of y corresponds to y 1 , and the second column corresponds to y 2 .

Plot the solutions for y 1 and y 2 against t .

Pass Extra Parameters to ODE Function

ode45 works only with functions that use two input arguments, t and y . However, you can pass extra parameters by defining them outside the function and passing them in when you specify the function handle.

Rewriting the equation as a first-order system yields

y 1 ′ = y 2 y 2 ′ = A B t y 1 .

odefcn , a local function included at the end of this example, represents this system of equations as a function that accepts four input arguments: t , y , A , and B .

Solve the ODE using ode45 . Specify the function handle so that it passes the predefined values for A and B to odefcn .

Plot the results.

Solve ODE with Multiple Initial Conditions

For simple ODE systems with one equation, you can specify y0 as a vector containing multiple initial conditions. This technique creates a system of independent equations through scalar expansion, one for each initial value, and ode45 solves the system to produce results for each initial value.

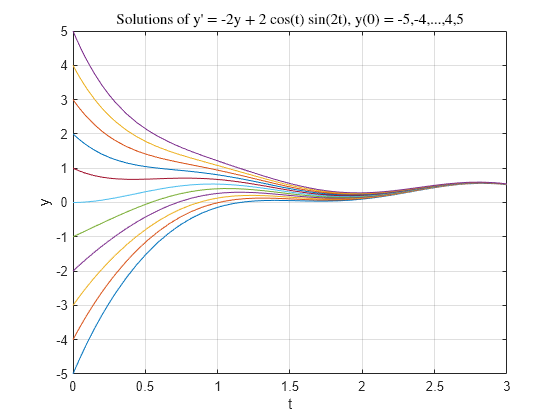
Create an anonymous function to represent the equation f ( t , y ) = — 2 y + 2 cos ( t ) sin ( 2 t ) . The function must accept two inputs for t and y .

Create a vector of different initial conditions in the range [ — 5 , 5 ] .

Solve the equation for each initial condition over the time interval [ 0 , 3 ] using ode45 .

Plot the results.

This technique is useful for solving simple ODEs with several initial conditions. However, the technique also has some tradeoffs:

You cannot solve systems of equations with multiple initial conditions. The technique only works when solving one equation with multiple initial conditions.

The time step chosen by the solver at each step is based on the equation in the system that needs to take the smallest step. This means the solver can take small steps to satisfy the equation for one initial condition, but the other equations, if solved on their own, would use different step sizes. Despite this, solving for multiple initial conditions at the same time is generally faster than solving the equations separately using a for -loop.

ODE with Time-Dependent Terms

Consider the following ODE with time-dependent parameters

The initial condition is 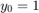. The function f(t) is defined by the n-by-1 vector f evaluated at times ft . The function g(t) is defined by the m-by-1 vector g evaluated at times gt .

Create the vectors f and g .

Write a function named myode that interpolates f and g to obtain the value of the time-dependent terms at the specified time. Save the function in your current folder to run the rest of the example.

The myode function accepts extra input arguments to evaluate the ODE at each time step, but ode45 only uses the first two input arguments t and y .

Solve the equation over the time interval [1 5] using ode45 . Specify the function using a function handle so that ode45 uses only the first two input arguments of myode . Also, loosen the error thresholds using odeset .

Plot the solution, y , as a function of the time points, t .

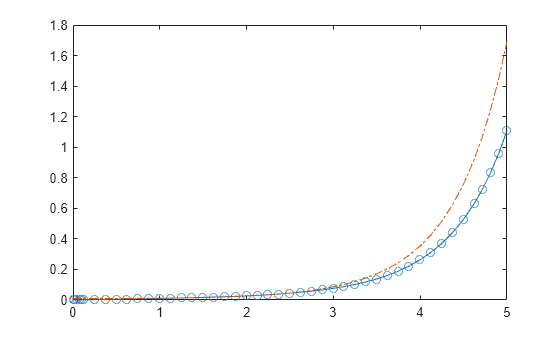
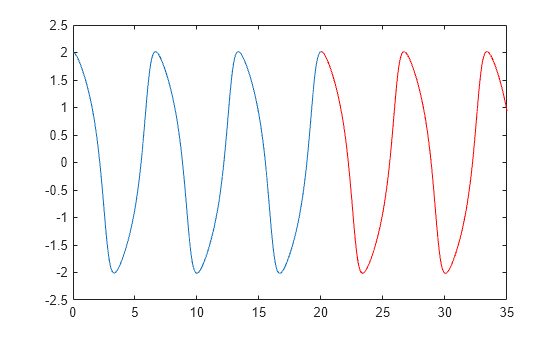
Evaluate and Extend Solution Structure

The van der Pol equation is a second order ODE

y 1 ′ ′ — μ ( 1 — y 1 2 ) y 1 ′ + y 1 = 0 .

Solve the van der Pol equation with μ = 1 using ode45 . The function vdp1.m ships with MATLAB® and encodes the equations. Specify a single output to return a structure containing information about the solution, such as the solver and evaluation points.

Use linspace to generate 250 points in the interval [0 20] . Evaluate the solution at these points using deval .

Plot the first component of the solution.

Extend the solution to t f = 3 5 using odextend and add the result to the original plot.

Видео:Nonlinear Oscillator Examples: Driven Van der Pol EquationСкачать

Input Arguments

odefun — Functions to solve
function handle

Functions to solve, specified as a function handle that defines the functions to be integrated.

The function dydt = odefun(t,y) , for a scalar t and a column vector y , must return a column vector dydt of data type single or double that corresponds to f ( t , y ) . odefun must accept both input arguments t and y , even if one of the arguments is not used in the function.

For example, to solve y ‘ = 5 y − 3 , use the function:

For a system of equations, the output of odefun is a vector. Each element in the vector is the solution to one equation. For example, to solve

y ‘ 1 = y 1 + 2 y 2 y ‘ 2 = 3 y 1 + 2 y 2

use the function:

For information on how to provide additional parameters to the function odefun , see Parameterizing Functions.

Example: @myFcn

Data Types: function_handle

tspan — Interval of integration
vector

Interval of integration, specified as a vector. At a minimum, tspan must be a two-element vector [t0 tf] specifying the initial and final times. To obtain solutions at specific times between t0 and tf , use a longer vector of the form [t0,t1,t2. tf] . The elements in tspan must be all increasing or all decreasing.

The solver imposes the initial conditions given by y0 at the initial time tspan(1) , and then integrates from tspan(1) to tspan(end) :

If tspan has two elements [t0 tf] , then the solver returns the solution evaluated at each internal integration step within the interval.

If tspan has more than two elements [t0,t1,t2. tf] , then the solver returns the solution evaluated at the given points. However, the solver does not step precisely to each point specified in tspan . Instead, the solver uses its own internal steps to compute the solution, and then evaluates the solution at the requested points in tspan . The solutions produced at the specified points are of the same order of accuracy as the solutions computed at each internal step.

Specifying several intermediate points has little effect on the efficiency of computation, but can affect memory management for large systems.

The values of tspan are used by the solver to calculate suitable values for InitialStep and MaxStep :

If tspan contains several intermediate points [t0,t1,t2. tf] , then the specified points give an indication of the scale for the problem, which can affect the value of InitialStep used by the solver. Therefore, the solution obtained by the solver might be different depending on whether you specify tspan as a two-element vector or as a vector with intermediate points.

The initial and final values in tspan are used to calculate the maximum step size MaxStep . Therefore, changing the initial or final values in tspan can cause the solver to use a different step sequence, which might change the solution.

Example: [1 10]

Example: [1 3 5 7 9 10]

Data Types: single | double

Видео:Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

Уравнение ван дер поля матлаб

Дифференциальные уравнения и системы уравнений

Для решения дифференциальных уравнений и систем в MATLAB предусмотрены следующие функции ode45(f, interval, X0 [, options]), ode23(f, interval, X0 [, options]), ode113(f, interval, X0 [, options]), odel5s(f, interval, X0 [, options]), ode23s(f, interval, X0 [, options]), ode23t (f, interval, X0 [,options]) и ode23tb(f, interval, X0 [, options]).

Входными параметрами этих функций являются:

• f — вектор-функция для вычисления правой части уравнения системы уравнений
• interval — массив из двух чисел, определяющий интервал интегрирования дифференциального уравнения или системы;
• Х0 — вектор начальных условий системы дифференциальных систем
• options — параметры управления ходом решения дифференциального уравнения или системы.

Все функции возвращают:

• массив Т — координаты узлов сетки, в которых ищется решение;
• матрицу X, i-й столбец которой является значением вектор-функции решения в узле Тi

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

В М-файле с именем pr 7. m пишем:

Потом в командном окне вызываем функцию ode113:

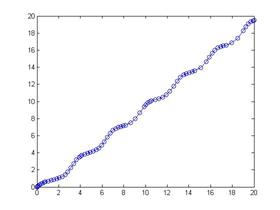
ode113(@pr7,[0 20],0) %Метод Адамса: @ pr 7 – ссылка на М-функцию, [0 20]- интервалы интегрирования,0 — условие: y(0)=0

Результатом будет график:

Необходимо реализовать метод Рунге-Кутта 4 порядка и решить задачу Коши для предложенной системы дифференциальных уравнений:

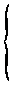
В М-файле с именем pr 8. m пишем:

Потом в командном окне вызываем функцию ode 45:

💡 Видео

Phase portrait of a Van der Pol oscillatorСкачать

Van der Pol Oscillator (mu = 0.8)Скачать

Car-trailer robot following Van Der Pol vector fieldСкачать

Билеты №32, 33 "Уравнения Максвелла"Скачать

Обучение в MATLAB и Simulink: от уравнения к фундаментальным принципамСкачать

Nonlinearity dependence of numerical solution of the van der Pol equation(phase space).Скачать

Synchronization of coupled Van der Pol oscillators #shortsСкачать

Comparison of 3 patterns of Van der Pol Equation [gnuplot]Скачать

Пример решения уравнения в MathCAD 14 (33/34)Скачать

ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

1 Одно уравнениеСкачать

Решение дифференциальных уравнений в вычислительной среде Mathcad с помощью функционала Rkadapt .Скачать

"PVT" на русском для начинающих. Часть 5_1Скачать