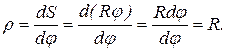- Введение
- Орты естественного трехгранника
- Скорость и ускорение точки в трехграннике Френе
- Как определить оси естественного трехгранника
- Для координатного и векторного способов задания движения
- Для естественного способа задания движения
- Пример определения ортов естественного трехгранника
- Оси естественного трехгранника
- Естественный способ задания движения точки
- Естественный способ задания движения точки
- Скорость движения точки
- Переход от координатного способа задания движения материальной точки к натуральному
- Натуральный трехгранник
- Кривизна кривой
- Касательное и нормальное ускорения точки в натуральных осях координат
- Некоторые случаи движения материальной точки
- 🌟 Видео
Видео:Свойства проекций катетов | Геометрия 8-9 классыСкачать

Введение
На странице “Кинематика материальной точки” мы установили, что вектор скорости движения точки направлен по касательной к траектории. Вектор ускорения лежит в соприкасающейся плоскости и его можно разложить на две составляющие. Одна составляющая направлена по касательной к траектории. Вторая составляющая направлена перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
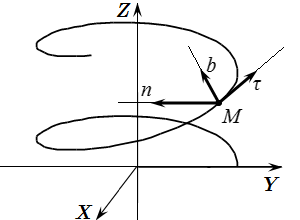
В некоторых случаях удобно ввести систему координат, связанную с текущим положением точки. Рассмотрим точку в определенный момент времени. Считаем, что нам известна траектория ее движения. Проведем через точку три прямых – касательную к траектории, главную нормаль и бинормаль. Главная нормаль перпендикулярна касательной и направлена в сторону мгновенного центра кривизны траектории. Бинормаль перпендикулярна касательной и главной нормали. Выберем систему координат с началом в точке и осями, направленными вдоль этих прямых. Такую систему координат называют естественным трехгранником Френе. Оси этой системы координат называются осями естественного трехгранника.
Видео:Естественный трехгранникСкачать

Орты естественного трехгранника
Пусть , и – единичные векторы, направленные вдоль касательной, главной нормали и бинормали к траектории, соответственно. Эти векторы являются ортами выбранной нами системы координат или ортами естественного трехгранника. Рассмотрим вопрос о выборе направления этих векторов.
Единичный вектор направлен вдоль касательной к траектории. Поэтому можно выбрать два взаимно противоположных направления. Самый удобный способ – это направить вдоль вектора скорости точки. Тогда
.
Однако, это не всегда можно сделать. Встречаются случаи, когда траектория движения заранее известна, а скорость – нет. Например, при движении точки по желобу внутри твердого тела под действием внешних сил. В таких случаях направление вектора выбирают заранее. Например, в сторону возрастания дуговой координаты.
Направление единичного вектора главной нормали определено однозначно. Он направлен перпендикулярно , в сторону мгновенного центра кривизны траектории.
Единичный вектор бинормали направлен перпендикулярно векторам и так, чтобы три вектора , и образовали правостороннюю систему координат:
.
Скорость и ускорение точки в трехграннике Френе
Применим формулы, которые мы вывели на странице “Кинематика материальной точки”.
То есть, в естественном трехграннике с ортами , скорость имеет одну компоненту:
.
Проекции вектора скорости на оси и трехгранника равны нулю. Проекцию скорости на направление единичного вектора касательной к траектории : , иногда называют алгебраической величиной скорости. Она отличается от модуля скорости только тем, что может иметь отрицательное значение: . При , скорость направлена вдоль вектора . При – в противоположную сторону.
Здесь и далее модуль скорости мы обозначаем либо символом с прямыми скобками , , либо просто символом без стрелки :
.
Ускорение имеет две компоненты:
,
Через них выражается касательное и нормальное ускорения:
.
Они являются проекциями вектора ускорения на оси и естественного трехгранника:
.
Их можно выразить через компоненту скорости и радиус кривизны траектории :
.
Компонента может быть как положительной (вектор сонаправлен с ), так и отрицательной (вектор противоположен ): . Компонента всегда положительна либо равна нулю: .
Проекция вектора ускорения на ось равна нулю:
.
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как определить оси естественного трехгранника
Далее мы считаем, что у нас есть неподвижная система координат . Материальная точка совершает движение. Требуется найти оси естественного трехгранника. То есть определить проекции ортов , и в системе координат .
Для координатного и векторного способов задания движения
Для координатного и векторного способов задания движения точки, формулы для определения ортов представлены на странице “Кинематика материальной точки”. На странице “Координатный способ задания движения точки” разобран пример вычисления компонентов векторов .
То есть, чтобы определить орты естественного трехгранника, нужно найти компоненты векторов скорости и нормального ускорения , применяя следующие формулы:
;
;
;
.
Далее определяем орты естественного трехгранника:
;
;
.
Для естественного способа задания движения
При естественном способе задания движения точки нам известна траектория ее движения. Поэтому перед нами стоит задача – по известной траектории, определить орты естественного трехгранника. Если траектория представляет собой простую геометрическую фигуру, например окружность, то определить векторы , и можно геометрически.
В общем, и более сложном случае, нужно представить уравнение траектории в параметрическом виде. Для этого вводим параметр . Это можно сделать многими способами. Поэтому желательно выбрать наиболее удобное представление.
Пусть, например, траекторией движения является эллипс, лежащий в плоскости :
.
Наиболее удобное параметрическое представление можно получить, если воспользоваться тригонометрической формулой:
.
Тогда уравнение траектории имеет вид:
Здесь – параметр.
Это не единственный способ получить параметрическое представление. Можно, например, разрешить уравнение эллипса относительно :
.
Применяя эту формулу, получим другое параметрическое представление:
Далее считаем, что эти параметрические уравнения описывают движение материальной точки, в котором параметр играет роль времени. Тогда, для определения осей трехгранника, можно применить формулы, применяемые для векторного и координатного способов задания движения. Вычисленные, таким образом, скорость и ускорение будут зависеть от выбранного параметрического представления. Но геометрические характеристики траектории, такие как орты , , и радиус кривизны траектории не зависят от выбранного параметрического представления.
Итак, чтобы найти орты естественного трехгранника по заданной траектории движения, нужно представить уравнение траектории в параметрическом виде и применить формулы, применяемые при координатном способе задания движения.
Пример определения ортов естественного трехгранника
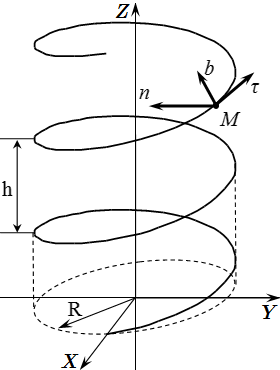
Найти единичные векторы в направлении осей естественного трехгранника, а также радиус кривизны траектории, для цилиндрической винтовой линии с радиусом основания и шагом .
Выберем систему координат . Ось направим вдоль оси винтовой линии. Тогда уравнение линии можно представить в следующем параметрическом виде:
(1)
Здесь – параметр; . Если взять проекцию точки линии, на плоскость , то – это угол между осью и проекцией . При увеличении на , координаты и точки возвращаются в первоначальной положение, а координата увеличивается на .
Считаем, что уравнения (1) описывают движение точки по винтовой линии. Определяем кинематические величины для такого движения.
Дифференцируя уравнения (1) по , находим компоненты вектора скорости:
;
;
.
Квадрат скорости:
.
Модуль скорости:
.
Единичный вектор в направлении касательной к траектории:
.
Мы выбрали направление вектора , совпадающим с направлением скорости. Поэтому
.
Дифференцируя компоненты вектора скорости по , находим компоненты вектора ускорения:
;
;
.
Проекция ускорения на направление вектора :
.
Этот результат можно получить и более простым способом. Для этого учтем, что модуль скорости и, следовательно , не зависит от . Тогда:
.
Вектор касательного ускорения:
.
Вектор нормального ускорения:
.
Квадрат вектора нормального ускорения:
.
Модуль вектора нормального ускорения:
.
Радиус кривизны траектории:
.
Единичный вектор в направлении главной нормали траектории:
.
Единичный вектор в направлении бинормали:
.
Автор: Олег Одинцов . Опубликовано: 14-03-2016 Изменено: 27-01-2020
Видео:Математика это не ИсламСкачать

Оси естественного трехгранника
ЕСТЕСТВЕННЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Содержание: естественный способ задания движения точки. Определения. Оси естественного трехгранника. Скорость и ускорение точки в проекциях на оси естественного трехгранника, касательное и нормальное ускорение точки.
Определения

(рис. 3.1):
– траектория движения точки;
– начало и направление увеличения дуговой координаты;
– уравнение движения точки по траектории, как функция времени: 
Для задания уравнения движения точки по траектории необходимо выбрать на заданной траектории точку О, принимаемую за начало отсчета дуговой координаты (рис. 3.1). Будем называть положительным то направление, которое соответствует возрастанию дуговой координаты. Обычно за 
Движение точки может быть задано различными способами, например таблицей значений, графиком, одной или несколькими функциями.
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
Рассмотрим движение точки, уравнение движения которой можно задать аналитически. Пусть шар падает вертикально вниз. В табл. 3.1 даны значения: время в секундах, расстояния в метрах. За нулевой момент времени выбираем момент начала падения шара. Через 1с после начала падения шар пролетает 5м, через 2 с – 20 м, через 3 с – 45 м (табл. 3.1).
Расписание движения падающего шара
 | 1 | 2 | 3 | 4 | 5 | 6 |
| S, м | 5 | 20 | 45 | 80 | 125 | 180 |
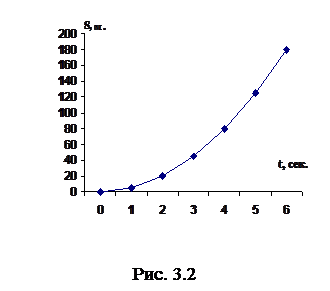
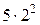
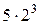

(рис. 3.2), то получим график зависимости пути, пройденному шаром от времени падения – графиком является парабола, которая описывается формулой
Сравним два вида задания движения – координатный и естественный. Если движение точки задано координатным способом: 
1. Составить и построить уравнение траектории – 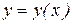
2. Отметить положение точки в начальный момент времени и направление движения;
3. Составить уравнение движения точки по траектории, как функция времени: 
Первые два пункта разобраны в предыдущей лекции. Покажем, как вычисляется уравнение движения точки, как функция дуговой координаты со временем — S(t).
Известно, что если точка движется в плоскости 

При 
Дифференциал дуги 


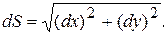
 Рис. 3.3 Рис. 3.3 | Интегрируя выражение (3.1), получим уравнение движения точки по криволинейной траектории, как функция времени:  (3.2) (3.2) |
Здесь 
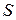

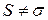

Справка. Для расстановки пределов интегрирования в (3.3) нужно исследовать заданную функцию движения 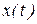 на экстремум, т.е. нужно определить знак первой производной от функции движения на экстремум, т.е. нужно определить знак первой производной от функции движения  для для  , при которых , при которых  . Тогда при . Тогда при  ,функция ,функция 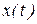 имеет экстремум, а точка меняет направление движения. имеет экстремум, а точка меняет направление движения. |
Пример 3.1.Точка М движется прямолинейно, согласно уравнению

Вычислить путь 
Решение. Вычислим направление скорости точки. Имеем:
Вектор скорости 



Точка за 5с. прошла
Пример 3.3.Движение точки М задано уравнением:

Вычислить путь 
Решение. Вычислим направление скорости точки. Имеем:

Вектор скорости 

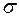


Оси естественного трехгранника
 Рис. 3.4 Рис. 3.4 |
Пусть задана криволинейная траектории движущейся точки М, рис. 3.4. Если к движущейся точке «привязать» касательную, то вследствие «искривленности» кривой эта касательная с перемещением точки касания будет вращаться. Этим “кривая” отличается от “прямой”, для которой касательная сохраняет одно и то же направление для всех точек.
Пусть точка М за время 

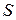




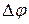
Определения
Принято кривизну кривой характеризовать углом поворота касательной, рассчитанным на единицу длины дуги.
Кривизной кривой Кв точке М называют предел
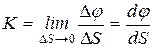
Замечание: для прямой – 
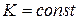
Радиусом кривизны кривой r в точке М называют величину, обратную кривизне кривой в этой точке,

Рассмотрим физический смысл радиуса кривизны. Во многих исследованиях представляется удобным приближенно заменить кривую вблизи рассматриваемой точки – окружностью, имеющей ту же кривизну, что и кривая в этой точке. Радиус этой окружности называется радиусом кривизны кривой в данной точке.
Вычислим радиус кривизны окружности (рис.3.5).
Дуга окружности длиной S, опирающаяся на центральный угол j, связана с радиусом окружности зависимостью S=Rj.
Имеем
Для прямолинейной траектории угол Dj =0, тогда  |
Построение осей естественного трехгранника. Проведем к точке 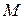




Точка движется в соприкасающейся плоскости.
Перпендикулярно 

Прямая, перпендикулярная главной нормали и касательной, называется бинормальной осью Мb. Единичный вектор 
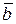

Три взаимно перпендикулярные прямые Мτ, Мn, Мb, положительные направления которых совпадают с направлениями единичных векторов 

Видео:Определение натуральной величины треугольника АВС методом вращения вокруг горизонтали или фронталиСкачать

Естественный способ задания движения точки
Содержание:
Естественный способ задания движения точки состоит в том, что в нём задаются: – траектория движения; – начало и положительное направление отсчета; – закон движения точки по траектории.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Видео:Геометрия 8. Урок 10 - Теорема Пифагора. Наклонная и проекция.Скачать

Естественный способ задания движения точки
Определим сначала кинематическое уравнение движения при натуральном способе задания движения материальной точки.
Натуральный способ задания (описания) движения материальной точки применяется тогда, когда траектория точки заранее известна. Движение изучается относительно фиксированного начала отсчета. Задается и закон движения материальной точки вдоль траектории.
Таким образом, для задания движения натуральным способом необходимо знать:
1. Траекторию АВ (рис. 2.3), которая может быть задана уравнением, графически или указанием, например точка движется вдоль окружности радиусом R.
2. Начало отсчета О криволинейной координаты S на траектории движения с указанием положительных «+» и отрицательных «–» значений. Кроме того, задается начало отсчета времени t. Обычно принимают, что t = 0 в момент, когда точка M проходит через точку O на траектории движения.
3. Закон движения материальной точки вдоль траектории. если, например, в момент времени t точка занимает положение M, криволинейная координата которого равна S, то это записывается следующим образом:
Эта функция должна быть непрерывной и по крайней мере дважды дифференцированной.
Соотношение называется кинематическим уравнением движения материальной точки в натуральной форме (или законом изменения криволинейной координаты). Это фактически расстояние подвижной точки M от начала отсчета вдоль траектории движения.
Криволинейную координату не следует путать с длиной пути, который проходит точка за определенный промежуток времени как в положительном, так и в отрицательном направлениях.
Определим кинематические характеристики движения материальной точки при
натуральном способе задания ее движения.
Скорость движения точки
Рассмотрим схему движения материальной точки M (рис. 2.3). Положение точки М соответствует моменту времени t, а положение М1 — t1. Тогда промежутку времени t1 – t = ∆t соответствует изменение криволинейной координаты S1 – S = ∆S. Отсюда можно определить среднюю скорость точки за промежуток времени ∆t:
А скорость точки в любой момент времени t можно определить, если взять предел отношения 
Модуль скорости материальной точки при натуральном способе задания ее движения равен первой производной по времени от закона движения точки.
Направление вектора скорости — по касательной к траектории движения материальной точки.
Производная по времени определяет численную алгебраическую величину скорости,
то есть, если 
отсчета, а если 
Решение.
Определим сначала положение точки на траектории движения при t1 = 1 c. Поскольку отсчет времени начался с началом момента движения, то S(0) = 0. Подставим в уравнение движения значение этого момента времени:
Для определения скорости движения точки продифференцируем по времени уравнения движения:
Из полученной функции скорости движения материальной точки можем определить (подстановкой t), что в начале движения (при t = 0): 

Переход от координатного способа задания движения материальной точки к натуральному
Для перехода от одного способа задания движения материальной точки к другому необходимо найти зависимости между основными параметрами этих движений. Сделаем это, рассматривая координатный и натуральный способы задания движения материальной точки. Так, на основании уравнения, что определяет скорость материальной точки при натуральном способе задания ее движения, можно записать
dS = 
Поскольку при координатном способе задания движения материальной точки ее скорость определяется согласно выражению:
то, подставляя его в предыдущее выражение, окончательно найдем зависимость между двумя указанными способами задания движения материальной точки:
Натуральный трехгранник
Приведем некоторые сведения из дифференциальной геометрии, которые понадобятся для определения кинематических характеристик движения материальной точки.
Предположим, что кривая АВ является траекторией точки М (рис. 2.4). В произвольной точке М и в бесконечно приближенной к ней точке М1 проведем касательные этой кривой (орты, подходящие этим касательным, обозначим через 




Плоскость, которая является предельным положением плоскости Q, когда точка M,
направляется к точке M, называется соприкасающихся плоскостью.
Через точку М проведем плоскость, перпендикулярную к касательной 

Линия пересечения нормали и стычной плоскостей определяет главную нормаль к кривой. Итак, главная нормаль — это единственная из бесконечного множества нормалей к кривой в точке M, которая расположена в соприкасающейся плоскости. Плоскость, проходящая через точку M перпендикулярна главной нормали, называется спрямляющей.
Линия пересечения спрямляющей и нормальной плоскостей определяет бинормаль
кривой. Очевидно, что бинормаль перпендикулярна к главной нормали.
Таким образом, в каждой точке кривой можно указать три взаимно перпендикулярные направления, по которым можно провести касательную в сторону роста дуговой координаты (соответствующий орт 





Прямоугольная подвижная система координатных осей с ортами 



Заметим, что плоская кривая полностью расположена в соприкасающейся плоскости, а главная нормаль является нормалью к кривой в этой плоскости. В отличии от других систем отсчета, натуральный трехгранник движется вместе с точкой и меняет свою ориентацию в пространстве в соответствии с характером траектории.
Кривизна кривой
Как видно дальше, ускорение точки в криволинейном движении зависит от кривизны траектории, поэтому рассмотрим эту характеристику. На рис. 2.5 изображена траектория AB движения точки и два близких положения M и M1. Проведем через точки M и M1 касающиеся 

Угол ∆φ между касательными в двух близких точках является углом смежности.
Кривизной кривой К в данной точке М называется предел отношения угла смежности к дуге ∆S, его взимает, когда эта дуга стремится к нулю.
Если, отношение ∆φ к ∆S является средней кривизной:
то, возведение Kc до границы дает истинное значение кривизны кривой:
Рассмотрим круг радиусом R (рис. 2.6). сделаем аналогичное геометрическое построение. Выразим ∆S по известной формуле:
и подставим в предыдущую формулу. Будем иметь:
K = 
Таким образом, круг радиусом R является кривой постоянной кривизны, значение которой равно обратной величине радиуса.
Для определения кривизны произвольной кривой достаточно подобрать такой круг, элемент дуги которого лучше всего аппроксимирует участок кривой в данной точке.
Тогда радиус круга будет радиусом кривизны кривой, а центр круга — центром кривизны.
Это показано на рис. 2.5:
K2 = 
Касательное и нормальное ускорения точки в натуральных осях координат
В декартовых осях координат мы определяли ускорение точки в проекциях на оси x, y, z. В натуральных осях координат определим проекции вектора ускорения на касательную 
равна нулю. Обратимся к рис. 2.7. Скорости близких точек M и M1 — векторы 



Перенесем параллельно вектор 



Параллельно ∆ 


и также будет расположен в соприкасающейся плоскости. А это значит, что проекция
вектора ускорения на бинормаль равна нулю.
Теперь, зная, что вектор ускорения имеет только касательную и нормальную составляющие, определим остальные.
Для этого нам понадобится схема, представленная рис. 2.8, где:
M 
M n — главная нормаль,
C — центр кривизны траектории,
ρ — радиус кривизны траектории.
Предположим, что в момент времени t точка M имеет скорость 


Переходим к проекциям ускорения материальной точки на натуральные оси координат 
Учитывая, что проекции векторов на параллельные оси одинаковы, проведем через точку М1 оси М1

Найдем проекции векторов 


Подставим значения проекций в выражения. Будем иметь:
Когда промежуток времени Δt стремится к нулю, то
Тогда уравнение может быть записано, как показано ниже, и касательное ускорение равно:
Таким образом, касательное ускорение материальной точки характеризует изменение скорости по величине в единицу времени и равна первой производной от функции скорости по времени или второй производной от закона движения.
Определим нормальное ускорение an. Преобразуем выражение для нормального ускорения, умножив числитель и знаменатель на произведение ∆φ · ∆S:
Перепишем выражение следующим образом:
Подставим значение этих границ в выражение для нормального ускорения:
Нормальное ускорение материальной точки характеризует изменение скорости по направлению в единицу времени и равна квадрату скорости, разделенном на радиус кривизны траектории в данной точке.
Вектор нормального ускорения 
Нормальное ускорение an всегда положительное, так как содержит в числителе выражение 

и отрицательным.
Вектор полного ускорения 


Угол φ между вектором 
Вектор ускорения 





где 

Следует отметить, что составляющие вектора 
Некоторые случаи движения материальной точки
1. Прямолинейное движение.
Радиус кривизны траектории, которой является прямая линия, равна 
Таким образом, скорость 

А если это движение еще и равномерно, то есть, когда 
2. Равномерное криволинейное движение.
В данном случае модуль скорости 

Таким образом, как видно из приведенных выражений, полное ускорение a материальной точки в этом случае равно нормальному ускорению an.
Вектор нормального (в данном случае полного) ускорения 


3. Равнопеременное криволинейное движение.
В этом случае движение точки является криволинейным, но ускорение a
величиной постоянной. Этот случай носит название равнопеременного движения (то есть, когда за равные промежутки времени скорость движения материальной точки изменяется на одну и ту же величину, увеличивается или уменьшается).
Определим кинематические характеристики равнопеременного движения материальной точки. Поскольку a


dv = a 
Скорость 








где 
Используем далее выражение 
dS = 
Вместо 
dS = 

Как и в предыдущем случае найдем перемещения S, взяв определенные интегралы от левой и правой частей последнего выражения. Также задаем верхние и нижние границы переменных величин, причем перемещение точки изменяется от начального значения So до конечного S:
Окончательно последнее выражение можно переписать так
где So — начальное перемещение точки.
Таким образом, при равнопеременном движении материальной точки ее скорость и перемещения определяются с помощью найденных выражений. Следует заметить, что знаки в правых частях этих формул (перед a
Пример:
Палец кривошипа дизеля движется в соответствии заданных параметрически уравнений
где x и y — в метрах; t — в секундах; b и ω — постоянные величины.
Определить траекторию движения, скорость и ускорение пальца.
Решение.
Для определения уравнения траектории движения пальца кривошипа надо исключить из заданных уравнений движения параметр времени t. Сначала определим с заданных уравнений тригонометрические функции
Поскольку тригонометрические функции являются функциями одного аргумента, то
поднимем к квадрату левые и правые части этих выражений и добавим их почленно:
Левая часть последнего выражения равна единице, поскольку sin cos 1 2 февраля t t , тогда sin 2 ω t + cos 2 ω t = 1, тогда
Таким образом, с последнего выражения видно, что траекторией движения пальца кривошипа является окружность радиуса b с центром в начале координат.
Для определения скорости движения найдем сначала проекции скорости движения пальца на координатные оси:
Модуль скорости движения будет равняться
Таким образом, с последнего выражения видно, что палец движется с постоянной скоростью, равной bω.
Найдем ускорение пальца кривошипа. Также определим его через проекции на оси координат. Для этого возьмем другие производные от заданных координат движения:
Полное ускорение будет равно:
Поскольку палец кривошипа движется по кругу, то есть по криволинейной траектории движения устойчивого радиуса b, то его ускорение можно было бы определить, если использовать выражения, описывающие натуральный способ задания движения материальной точки. Касательное ускорение пальца кривошипа будет равняться нулю, поскольку скорость bω = const. А именно:
Нормальное ускорение определим так:
Поскольку касательного ускорения нет, то полное ускорение равно нормальному:
Таким образом, как видим, ускорение пальца кривошипа, которое определено различными способами, совпадают.
Пример:
Точка на ободе барабана зерноуборочного комбайна в период разгона движется согласно уравнению S = 0,1 · t 3 (S — в метрах, t — в секундах). Радиус барабана равен R = 0,5 м. Определить касательное и нормальное ускорение точки в момент, когда его скорость равна 
Решение.
Уравнения движения точки задано натуральным способом, а потому скорость можно определить так:
По заданному значению скорости под углом 
Касательное ускорение точки будет равно:
или через 10 сек
a
Нормальное ускорение определим так:
Знак «+» перед касательным ускорением a
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🌟 Видео
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Черчение. 8 класс. Мазаева И.М. Изометрия и ДиметрияСкачать

Скалярное произведение векторов. 9 класс.Скачать

Дифференциальная геометрия | проекции на трёхгранник ФренеСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Построение проекции вектора на осьСкачать

Построение треугольника в трёх проекцияхСкачать

Математика | Соотношения между сторонами и углами в прямоугольном треугольнике.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Урок 9. Проекции вектора на координатные осиСкачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать