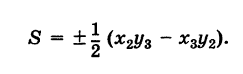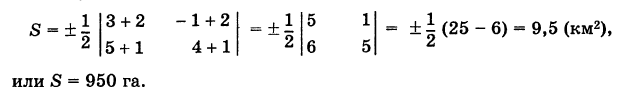Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
- Решить треугольник Онлайн по координатам
- Прямоугольная система координат на плоскости и ее применение с примерами
- Прямоугольная система координат на плоскости и ее применение к простейшим задачам
- Прямоугольные координаты точки на плоскости
- Преобразование прямоугольной системы координат
- Расстояние между двумя точками на плоскости
- Деление отрезка в данном отношении
- Площадь треугольника
- 🌟 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
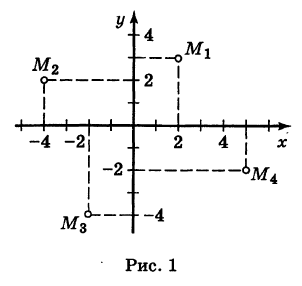
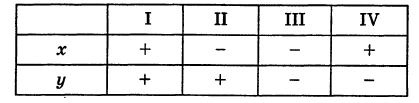
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнения стороны треугольника и медианыСкачать  Прямоугольная система координат на плоскости и ее применение с примерамиСодержание: Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Прямоугольная система координат на плоскости и ее применение к простейшим задачамПрямоугольные координаты точки на плоскостиКоординатами точки на плоскости называются числа, определяющие положение этой точки на плоскости. Прямоугольные декартовы координаты (по имени математика Декарта) на плоскости вводятся следующим образом: на этой плоскости выбираются точка О (начало координат) и проходящие через нее взаимно перпендикулярные направленные прямые Ох и Оу (оси координат) (рис. 1). Для удобства рассмотрения будем предполагать, что ось Ох 0ось абсцисс) горизонтальна и направлена слева направо, а ось Оу (ось ординат) вертикальна и направлена снизу вверх; таким образом, ось О у повернута относительно оси Ох на угол 90° против хода часовой стрелки 1 ). Кроме того, выбирается единица масштаба для измерения расстояний. Для данной точки М введем в рассмотрение два числа: абсциссу х и ординату у этой точки. Абсциссой х называется число, выражающее в некотором масштабе расстояние от точки до оси ординат, взятое со знаком плюс, если точка лежит вправо от оси ординат, и со знаком минус, если точка лежит влево от оси ординат. Ординатой у называется число, выражающее в некотором масштабе (обыкновенно в том же, как и для абсциссы) расстояние от точки до оси абсцисс, взятое со знаком плюс, если точка лежит выше оси абсцисс, и со знаком минус, если точка лежит ниже оси абсцисс. Эти два числа х и у и принимаются за координаты точки М, так как они полностью определяют положение точки на плоскости, а именно: каждой паре чисел х и у соответствует единственная точка, координатами которой являются эти числа; и обратно, каждая точка плоскости имеет определенные координаты х и у. Если точка М имеет координаты х и у, то это обстоятельство обозначают так: М (х, у) (на первом месте ставится абсцисса х, а на втором — ордината у). При записи координат знак плюс, как обычно, можно опускать. Оси Ох и Оу разбивают плоскость на четыре части, называемые квадрантами. Производя нумерацию квадрантов (I, II, III и IV) в направлении против хода часовой стрелки, отправляясь от того квадранта, где обе координаты положительны, получим следующую таблицу знаков координат: Отрезок ОМ у соединяющий начало координат О с точкой М (рис. 2), называется ее радиусом-вектором. Обозначая через ф угол, образованный отрезком ОМ с положительным направлением оси Ох, и через Нетрудно убедиться, что формулы (1) будут справедливы для координат точек всех квадрантов. Таким образом, знак абсциссы х точки М совпадает со знаком косинуса, а знак ее ординаты у — со знаком синуса в соответствующем квадранте. Легко видеть, что если точка лежит на оси абсцисс, то ее ордината у равна нулю; если же она лежит на оси ординат, ее абсцисса х равна нулю, и обратно. Следовательно, если точка совпадает с началом координат, то равны нулю обе ее координаты. В дальнейшем прямоугольные декартовы координаты для краткости будем называть просто прямоугольными координатами. В следующих параграфах рассмотрим некоторые простейшие задачи на применение прямоугольных координат на плоскости. Преобразование прямоугольной системы координатПри решении задач иногда выгодно вместо данной прямоугольной системы координат Возникает вопрос о том, как от одной системы координат перейти к другой. Рассмотрим сначала простейший случай (рис. 3), когда оси «новой системы координат» О’х’у’ параллельны соответствующим осям «старой системы координат о Оху и имеют одинаковые направления с ними (параллельный перенос системы координат). Пусть начало новой системы координат — точка О’ — имеет координаты (а, Ь) в старой системе координат. Точка М плоскости со «старыми координатами» (х, у) будет иметь некоторые «новые координаты» [х у’] (для ясности мы их обозначаем квадратными скобками). Из рис. 3 непосредственно получаем х’ = х — а, у’ = у — b, (1) т. е. новые координаты точки равны ее старым координатам минус старые координаты нового начала. Обратно, из (1) находим х = х’ + а, у = у’ + Ь. (2) Пусть теперь «новая система» координат Ох’у при неизменном начале О, повернута относительно «старой системы» Оху на угол а (рис. 4), т. е. Обозначим через Так как новые координаты точки М, очевидно, есть то из формул (3) и (4) получаем Для запоминания формул (6) используют следующий мнемонический прием: говорят, что первая формула (6) содержит полный беспорядок, а вторая — полный порядок. Действительно, в первой формуле на первом месте стоит cos, на втором — sin; кроме того, присутствует знак минус. Во второй формуле (6) никаких нарушений правильности в этом смысле нет. Формулы (6) выражают старые координаты х и у точки М через ее новые х’ и у’. Чтобы выразить новые координаты х’ и у’ через старые х и у, достаточно разрешить систему (6) относительно х’и у’. Однако можно поступить проще, а именно принять систему Ох’у’ за «старую», а систему Оху за «новую». Тогда, учитывая, что вторая система повернута относительно первой на угол — а, заменяя в формулах (6) х’ и у’ соответственно на х и у и обратно и принимая во внимание, что cos (-a) = cos a, sin (-a) = -sin a, будем иметь Наконец, в общем случае, когда новое начало координат есть точка О’ (a, Ь) и ось О’х’ образует с осью Ох угол а, соединяя формулы (2) и (6), находим Здесь угол Р считается положительным, если радиус-вектор ОМ повернут относительно оси Ох’ против хода часовой стрелки, и отрицательным, если он повернут относительно этой оси по ходу часовой стрелки. Аналогично, из формул (1) и (7) получаем Из формул (8) и (9) вытекает, что формулы перехода от одной прямоугольной системы координат к другой прямоугольной системе координат являются линейными функциями как новых, так и старых координат, т. е. содержат эти координаты в первой степени. Пример: Отрезок ОМ, где точка М имеет координаты (х, г/), повернут на угол а = 120° против хода часовой стрелки (рис. 5). Каковы будут координаты х’ и у’ нового положения М’ точки М? Решение: Предполагая, что с точкой М связана подвижная система координат Ох’у на основании формул (6) будем иметь Расстояние между двумя точками на плоскости1) Найдем сначала расстояние г от начала координат О (0, 0) до точки М (х, у) (рис. 6). Расстояние г = ОМ, очевидно, является гипотенузой прямоугольного Таким образом, расстояние от начала координат до некоторой точки равно корню квадратному из суммы квадратов координат этой точки. 2) В общем случае, пусть для точек A Выберем новую систему координат Ах’у’ начало которой совпадает с точкой А и оси которой параллельны прежним осям и имеют, соответственно, одинаковые направления с ними. Тогда в новой системе координат точки Л и В будут иметь координаты А [0, 0] и Б т. е. расстояние между двумя точками плоскости (при любом их расположении) равно корню квадратному из суммы квадратов разностей одноименных координат этих точек. Замечание. Формула (2) дает также длину отрезка АВ. Легко определить направление этого отрезка. Из прямоугольного А ABC имеем (dx и dy называются проекциями отрезка АВ на оси координат Оху). Отсюда получаем Пример: Танк на местности переместился из точки А (-30, 80) в точку Б (50, 20) (относительно некоторой системы координат Оху)> причем координаты точек даны в километрах. Найти путь d, пройденный танком, если он двигался, не меняя направления. Решение: Применяя формулу (2), имеем Деление отрезка в данном отношенииПредположим, что отрезок АВ (рис. 8), соединяющий точки A (xl9 уг) и В (x2t у2), разделен точкой С на два отрезка АС и СБ, причем отношение АС к СБ равно I (I > 0): Требуется выразить координаты х и у точки С(х, у) через координаты концов отрезка АВ. Опустим перпендикуляры откуда на основании равенства (1) будем иметь Из рис. 8 видно, что Решая уравнение (3) относительно неизвестной абсциссы х, будем иметь т. е. координаты середины отрезка равны полусуммам соответствующих координат его концов. Примечание. При выводе формул (4) и (5) мы предполагали, что концы А и В отрезка АВ лежат в первом квадранте и, следовательно, координаты точек Аи В положительны. Легко доказать, что формулы (4) и (5) будут справедливы и в случае произвольного расположения отрезка АВ на координатной плоскости. Пример: Вычислить координаты точки С (х, у)> делящей отрезок АВ между точками А (-5, -3) и В (4, -6) в отношении АС/СВ = 3/2. Решение: В этом случае I = 3/2 и, следовательно, Площадь треугольникаПусть требуется найти площадь S треугольника ABC (рис. 9) с вершинами Пусть АВ = с, АС = Ь, а углы, образованные этими сторонами с осью Ох, соответственно равны На основании (см. замечание) имеем (рис. 9) и Пусть Отсюда в силу (1) и (2) имеем Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус. Поэтому формулу для площади треугольника обычно пишут в виде где знак выбирается так, чтобы для площади получалось положительное число, Используя понятие определителя второго порядка формулу (4′) можно записать в удобной для запоминания форме: Формула (4′) упрощается, если точка А Отметим, что если точки А, В, С находятся на одной прямой, то площадь S = 0; и обратно, если S = 0, то вершины А, Б и С расположены на одной прямой. Пример: Вспаханное поле имеет форму треугольника с вершинами А (-2, -1), В (3, 5) и С (-1, 4) (размеры даны в километрах). Определить площадь S этого поля. По формуле (5) имеем Замечание. Вычисление площади многоугольника сводится к вычислению площадей треугольников. Для этого достаточно разбить многоугольник на треугольники, площади которых вычисляют по формуле (4).
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 🌟 ВидеоДаны координаты вершин треугольника АВС.Скачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Вычисляем высоту через координаты вершин 1Скачать  Видеоурок "Координатная плоскость, координата точки"Скачать  Уравнение прямой и треугольник. Задача про высотуСкачать  найти уравнения биссектрис углов между прямымиСкачать  Задача, которую боятсяСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Построение треугольника. Математика.Скачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Векторы. Метод координат. Вебинар | МатематикаСкачать  Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать  Вычисляем угол через координаты вершинСкачать  Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Аналитическая геометрия на плоскости. Решение задачСкачать  найти уравнение высоты треугольникаСкачать  | |||||
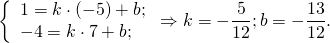
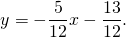
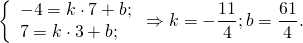
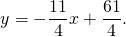
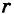 его длину, для точки М, лежащей в I квадранте, из треугольников ОММ’ и ОММ» получим
его длину, для точки М, лежащей в I квадранте, из треугольников ОММ’ и ОММ» получим 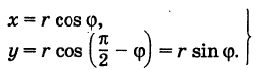
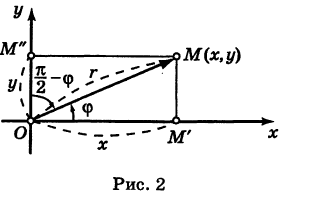
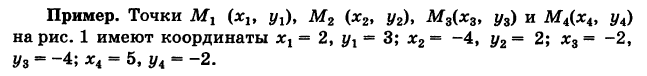
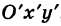 выбрать другую прямоугольную систему координат О’х’у определенным образом ориентированную относительно первой. Например, при межпланетных путешествиях можно пользоваться системой координат, связанной с центром Земли (геоцентрическая система координат); однако более удобно использовать систему координат, связанную с центром Солнца (гелиоцентрическая система координат).
выбрать другую прямоугольную систему координат О’х’у определенным образом ориентированную относительно первой. Например, при межпланетных путешествиях можно пользоваться системой координат, связанной с центром Земли (геоцентрическая система координат); однако более удобно использовать систему координат, связанную с центром Солнца (гелиоцентрическая система координат).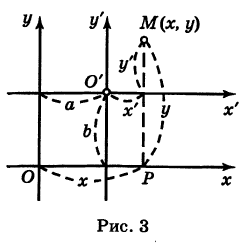
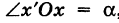 , причем а считается положительным, если поворот осуществляется против хода часовой стрелки, и отрицательным — в противоположном случае (поворот системы координат).
, причем а считается положительным, если поворот осуществляется против хода часовой стрелки, и отрицательным — в противоположном случае (поворот системы координат). 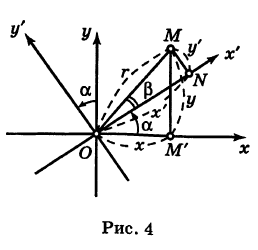
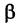 угол, образованный радиусом-вектором г = ОМ точки М с осью Ох’; тогда отрезок ОМ, с учетом знака угла
угол, образованный радиусом-вектором г = ОМ точки М с осью Ох’; тогда отрезок ОМ, с учетом знака угла 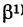 ), будет составлять с осью Ох угол
), будет составлять с осью Ох угол 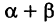 . Отсюда на основании формул (1) из при любом расположении точки М имеем
. Отсюда на основании формул (1) из при любом расположении точки М имеем
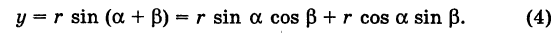
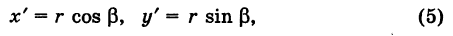
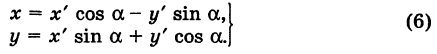
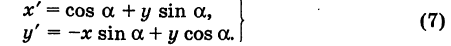
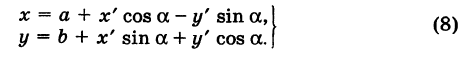
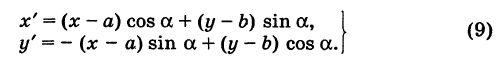

 ОММ’ с катетами
ОММ’ с катетами 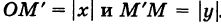 . По теореме Пифагора получаем
. По теореме Пифагора получаем
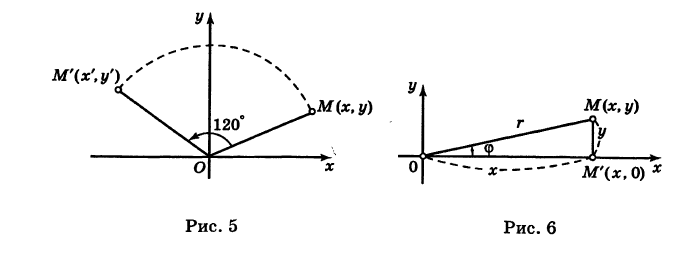
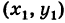 и Б
и Б 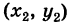 (рис. 7) требуется найти расстояние d = АВ между этими точками.
(рис. 7) требуется найти расстояние d = АВ между этими точками.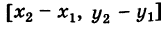 . Отсюда на основании формулы (1) получаем
. Отсюда на основании формулы (1) получаем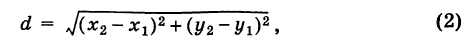
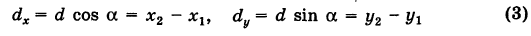
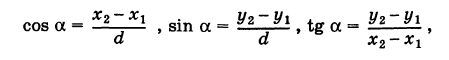 где d определяется формулой (2).
где d определяется формулой (2).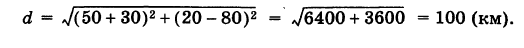

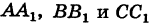 соответственно из точек А, В и С на ось Ох. Тогда получим, что три параллельные прямые
соответственно из точек А, В и С на ось Ох. Тогда получим, что три параллельные прямые 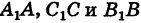 пересекают стороны угла (не обозначенного на рисунке), образованного прямыми АВ и Ох. Как известно из элементарной геометрии, пучок параллельных прямых рассекает стороны угла на пропорциональные части; поэтому
пересекают стороны угла (не обозначенного на рисунке), образованного прямыми АВ и Ох. Как известно из элементарной геометрии, пучок параллельных прямых рассекает стороны угла на пропорциональные части; поэтому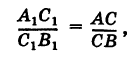

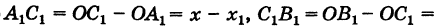 х2 — х. Подставляя эти выражения в формулу (2), получим
х2 — х. Подставляя эти выражения в формулу (2), получим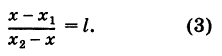
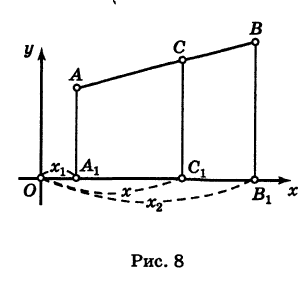
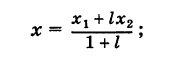
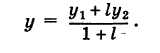 Итак, координаты точки С (ху у), делящей отрезок АВ в отношении / (считая от А к В), определяются формулами
Итак, координаты точки С (ху у), делящей отрезок АВ в отношении / (считая от А к В), определяются формулами 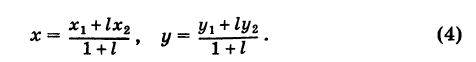 Если точка С делит отрезок АВ пополам, то АС = СВ и, следовательно, I = АС/СВ = 1. Обозначая координаты середины отрезка АВ через х, у, получим на основании формул (4)
Если точка С делит отрезок АВ пополам, то АС = СВ и, следовательно, I = АС/СВ = 1. Обозначая координаты середины отрезка АВ через х, у, получим на основании формул (4) 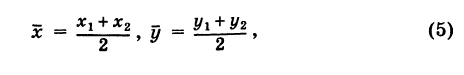
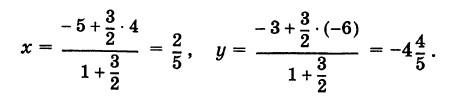
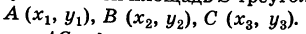
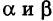 .
.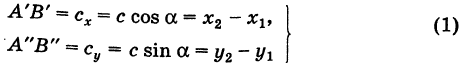
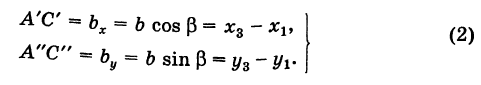
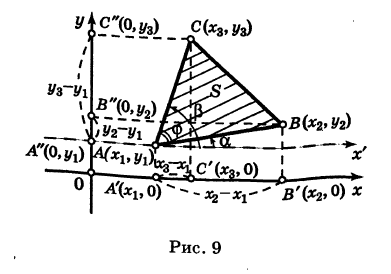
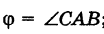 ; очевидно (рис. 9),
; очевидно (рис. 9), 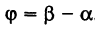 . По известной формуле тригонометрии получаем
. По известной формуле тригонометрии получаем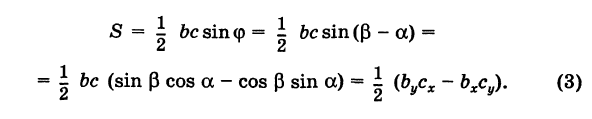
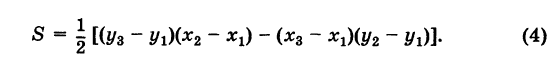
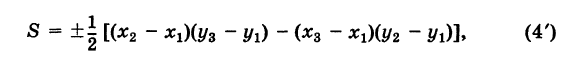
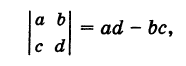
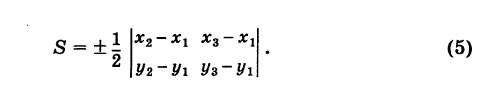
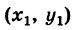 находится в начале координат. А именно, полагая
находится в начале координат. А именно, полагая 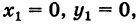 получим
получим