- Общие сведения
- Суть уравнения
- Доказательство закона
- Типовое задание
- Примеры высокого уровня
- Фазовые переходы и уравнение теплового баланса
- теория по физике 🧲 термодинамика
- Плавление и отвердевание
- Парообразование и конденсация
- Тепловые процессы при нагревании и охлаждении
- Частные случаи тепловых процессов
- Уравнение теплового баланса
- Взаимные превращения механической и внутренней энергии
- Примеры КПД
- Уравнение теплового баланса. Пособие Самарина
- Решение задач на теплообмен
- с использованием уравнения теплового баланса
- С 17 Самарин Г.Г. Решение задач на теплообмен с использованием уравнения теплового баланса: Методические рекомендации. – Киров: Издательство Лицея естественных наук, 2002. – 35 с.
- Задача 2
- Решение
- Решим задачу с помощью уравнения теплового баланса в виде (5).
- 1. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.
- t =
- Задача 3
- Задача 4
- Задача 5
- Задача 6
- Q затр — теплота, отданная горячей водой: Q затр = c 2 m 2 (t 2 ).
- Задача 7
- Задача 9
- В калориметр, содержащий 400 г воды и 200 г льда при 0 С, впустили водяной пар с температурой 100 С. Сколько пара было впущено в калориметр, если в калориметре установилась температура 20 С? Теплоёмкость калориметра 1000 Дж/ 0 С.
- В сосуд теплоёмкостью 1000 Дж/ 0 С, содержащий 5 кг воды при температуре 20 С, положили лёд, имеющий температуру 40 С. Температура образовавшейся смеси оказалась равна 2 С. Сколько льда было положено в сосуд?
- В алюминиевом калориметре массой 200 г находится кусок льда с температурой 20 С. В калориметр впустили водяной пар, имеющий температуру 100 С. Когда температура калориметра стала равна 20 С, измерили массу его содержимого. Она оказалась равной 400 г. Найти массу льда, находящегося в калориметре, и массу сконденсировавшегося пара.
- В калориметр, содержащий 3 кг воды при температуре 20 С, опустили 2 кг льда, имеющего температуру 10 С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
- В калориметр, содержащий 1 кг льда и 800 г воды при 0 С впускают 100 г водяного пара при 100 С. Что будет в калориметре, когда теплообмен прекратится? Теплоемкостью калориметра пренебречь.
- В калориметре находится вода массой 600 г при температуре 5 С. К ней долили ещё 300 г воды с температурой 10 С и положили 600 г льда с температурой 60 С. Что будет в калориметре после того, как теплообмен прекратится? Теплоемкостью калориметра пренебречь.
- В теплоизолированном медном сосуде массой 400 г находятся 2 кг льда при температуре 10 С. В сосуд помещают 400 г водяного пара при температуре 110 С. Что будет в сосуде после того, как теплообмен прекратится?
- В колбе находятся 200 г воды при температуре 0 С. Откачиванием паров всю воду в колбе заморозили. Сколько получилось льда?
Видео:ЕГЭ физика. Уравнение теплового баланса (термодинамика)Скачать

Общие сведения
Баланс в переводе на русский язык означает равновесие. Когда теплоизолированная система приходит в состояние теплового равновесия, то температура всех тел, образующих эту совокупность, становится одинаковой. Такую ситуацию называют законом теплового равновесия или нулевым уравнением термодинамики.
Впервые с уравнением теплового баланса знакомят в средней школе на уроке физики. Ученикам в седьмом классе предлагается решить несколько простых заданий, используя равенство. Формула и определение даётся без доказательства, так как для понимания процесса нужно знать понятия, которые разбираются в выпускных классах школы. Например, то, что теплоёмкость не является характеристикой вещества, при этом она может быть разной в зависимости от проходящих процессов.
Закон теплового баланса позволяет утверждать, что когда в изолированной системе физических тел происходит только теплообмен, то часть тепла, переданного телами, внутреннее состояние энергии которых уменьшается, численно равняется теплу, полученному объектами с возрастающей внутренней энергии. Математически уравнение записывается в виде следующей формулы: Q 1 + Q 2 + Q 3 + …+ Qn = 0, где:
- n — число тел, находящихся в теплоизолированной системе;
- Q — полученное количество теплоты.
Если предположить, что имеется совокупность, состоящая из двух тел, из которых одно отдаёт тепло, а другое принимает его, то справедливо будет записать: Q1 = Q2. Таким образом, теплоотдача всегда равняется теплоприёму. Поэтому этот закон и называют правилом сохранения энергии в тепловых процессах.
Когда тела два, то понять, какое из них отдаёт тепло, а какое получает, несложно. То, что имеет большее нагревание, — будет отдавать. Если же объектов три и более, и некоторые из них имеют промежуточную температуру, определить, какие из них принимают тепло, довольно сложно. Вот тут на помощь и приходит уравнение термодинамики.
Изменение внутренней энергии объясняется теплопередачей, то есть случаем, когда работа не совершается. Поэтому в физике уравнение теплового баланса используется при анализе процессов теплопередачи, нахождении КПД. Это равенство можно применять как при рассмотрении твёрдых тел, так и жидкости.
Видео:Урок 175. Уравнение теплового балансаСкачать

Суть уравнения
Следует рассмотреть процесс установления теплового равновесия в теплоизолированной системе. Это такая совокупность, в которой объекты взаимодействуют только друг с другом. Простейшая система будет состоять из двух тел. Например, в термос налит сок и в него вброшен лёд. В этом случае термос является изолятором от внешнего воздействия. Пусть первое тело имеет температуру t1, а второе t2. Допустим, что t1 больше t2. Это допущение не является принципиальным, поэтому его можно использовать.
В начальный момент времени тела находятся далеко друг от друга и теплообмен между ними не происходит. Как только, они соприкоснутся — начнётся взаимодействие. Так как температура первого тела больше, то оно начнёт остывать, а второе нагреваться. Происходит теплопередача. В какой-то момент времени она прекратится и наступит тепловое равновесие. То есть температура двух тел станет одинаковой: t1 = t2.
Получившаяся температура называется равновесной. Обозначается она греческой буквой тета — θ. Так как раньше первое тело имело большую температуру, то получается, что в процессе взаимодействия оно отдало тепло. Записать это можно как Q1 — — количество теплоты, отданное первым телом. Второй же объект в процессе подогрелся — увеличил температуру. Обозначить это можно как +Q2 — количество теплоты, полученное вторым телом.
Получить тепло второй объект мог только от первого тела, так как рассматриваемая система изолированная. Соответственно, и отдать определённое количество теплоты первое тело могло только второму. Отсюда можно сделать вывод, что если система теплоизолированная, то эти два количества теплоты одинаковы: Q1 — = +Q2. Фактически это есть уравнение баланса.
Такая запись даётся в школьных учебниках. Но профессиональные физики записывают его в другой форме. Для термодинамики неважно, какой объект отдаёт, а какой получает тепло. Наука изучает только количество теплоты, полученное в процессе. Взяв простую аналогию с весом, когда о похудевшем человеке на два килограмма можно сказать, что он поправился на минус два кило, будет верным записать: Q1 — = -Q1 или -Q1 = Q2.
Если собрать два слагаемых таким образом, чтобы они находились с одной стороны знака равенства, то можно записать: Q1 + Q2 = 0.
Суммарное количество теплоты, образуемое при теплообмене тел в теплоизолированной системе, равно нулю. При этом это правило будет справедливо и для энного количества объектов.
Видео:ИЗИ Физика. Уравнение теплового баланса. Фазовые переходыСкачать

Доказательство закона
Пусть имеется теплоизолированная система, состоящая из нескольких помещённых в неё объектов. Сами тела могут обмениваться теплом только друг с другом. Первый закон термодинамики для системы в целом можно записать как Q = А’ + Δ U. То есть количество теплоты, полученное всей системой, равняется суммарной работе, совершённой всеми телами в совокупности над внешним миром, складывающейся с изменением энергии всех тел внутри системы.
По условию задачи внутренняя энергия меняется не за счёт совершения работы. Поэтому А’ = 0. С другой же стороны, теплоизоляция обозначает, что Q = 0. Иными словами, количество энергии, поступающее из окружения Земли, равняется нулю. Следовательно, изменение внутренней энергии всех тел в системе будет нулевым: Δ U = 0.
Энергия системы состоит из внутренних энергий каждого из входящих в неё тел: U = U1 + U2 +…+ Un. Изменение же её Δ U = Δ U 1 + Δ U 2 + … + Δ Un. Отсюда следует, что если внутренняя энергия остаётся неизменной, то сумма Δ U будет нулевой: Δ U 1 + Δ U 2 + … + Δ Un = 0.
Первый закон термодинамики персонально для каждого из тел входящих в систему можно записать как следующую систему:
Все уравнения, входящие в неё, можно сложить почленно. При этом распределив слагаемые для удобства дальнейшего анализирования: Q1 + Q2 +…+ Q n = (А n1′ + А n2′ + … + А n’) + (Δ U1 + Δ U2 + … + Δ Un). Из полученного выражения можно сделать вывод, что сумма дельт второго члена в правой части равняется нулю. В первом же члене с правой стороны каждое слагаемое также равняется нулю. Поэтому можно записать: Q1 + Q2 +…+ Q n = 0. Что и следовало доказать.
Для решения задач полезно вспомнить, на что может идти полученное тепло. К таким частным случаям относят:
- Процессы, при которых нет фазовых переходов. В таком случае полученное количество идёт на увеличение теплоты потенциальной и кинетической энергии: Q = c * m * ΔT (изохорная теплоёмкость).
- Плавление. Например, есть тающий лёд, к которому подводят тепло, при этом кинетическая энергия остаётся постоянной. Значит, изменяется только потенциальная мощность. В этом случае происходит превращение льда в воду. Это действие называют плавлением — переход кристаллического вещества из твёрдого состояния в жидкое: Q = λ * m.
- Парообразование. Выделение из жидкости пара: Q = L * m.
Видео:10 класс, 11 урок, Уравнение теплового баланса с учетом изменения агрегатного состояния веществаСкачать

Типовое задание
Явление теплового баланса используется как в изучении процессов при переходе из одного агрегатного состояния в другое, так и для твёрдых или жидких тел, не изменяющих решётку. Существуют типовые задания, входящие в школьную программу. Ученик, решая их, научится находить удельные параметры и сможет понять всю важность выражения теплового баланса.
В латунный котёл массой 128 граммов, содержащий 240 граммов воды, при 8,4 градусах опущено металлическое тело массой 192 грамма, нагретое до 120 градусов Цельсия. Окончательная установившаяся температура составила 21,5 градус. Определить удельную теплоёмкость рассматриваемого тела. Для решения задачи необходимо из справочника взять значение энергетической теплоёмкости латуни. Она составляет 400 Дж/ кг *С 0 . При этом нужно учитывать, что котёл теплоизолирован.
Температуру, которая установилась через время, обозначают буквой θ. Решение подобных задач начинают с установления количества тел, участвующих в теплообмене. В этом примере их три: вода, котёл, испытываемое тело. Количество тепла, полученное всеми тремя объектами, согласно закону, будет равняться нулю: Qв + Qк +Qт = 0. Теперь следует каждое слагаемое расписать отдельно:
- Qв = mв * cв * Св (θ — Tв).
- Qк = mк * cл * (θ — Tв).
- Qт = mт * cт * (θ — Tк).
Полученные формулы нужно подставить в исходное уравнение. При этом следует обратить внимание, что при подстановке образуется общий множитель (θ — T в), который можно вынести за скобки: (m в * c в + m к * c л) * (θ — T в) + m т * c т * (θ — T к) = 0.
Из условия задачи известно, что у тела температура 100 градусов, а равновесная температура меньше. Поэтому последняя скобка будет отрицательной. Значит, есть смысл перенести это слагаемое вправо, поменяв местами вычитаемое и уменьшаемое: (m в * c в + m к * c л) * (θ — T в) = m т * c т * (T к — θ). Отсюда можно выразить удельную теплоёмкость массы тела. Она будет равняться: C т = (m в * c в + m к * c л) * (θ — T в) / m т * (T к — θ) .
Все данные, используемые в формуле, известны. Остаётся только провести расчёты, подставив значения: Cт = (0,24 кг * 4,2 кДж/кг*С + 0,128 кг * 0,4 кДж/кг*С *(21,5 — 8,4) С) / 0,192 кг * (100 — 21,5)С = 0,921 кДж/ кг *С 0 . Полученное вещество является алюминием.
Видео:Решение задач на уравнение теплового баланса. Физика 8 классСкачать

Примеры высокого уровня
Эти задачи рассчитаны на подготовленных учащихся, понимающих суть процессов и знающих уравнение баланса. Например, электрическая установка с мощностью P = 350 Вт не может нагреть воду массой 0,6 кг до кипения. Убедившись в этом, её выключают. Нужно определить, каким останется конечный нагрев воды через 15 секунд.
Из условия можно утверждать, что мощность теплопотерь равняется мощности нагревателя: Pпот = P. По сути, мощность теплопотерь это количество тепла, отдаваемое телом в единицу времени. То есть: P пот = Q — / ΔT. С другой стороны, отданное тепло находится из формулы: Q — = c * m * (-ΔT). Отсюда можно записать: P = — c * m * ΔT / Δt. Из последнего выражения легко выразить искомый параметр: ΔT = -(P * Δt) / (c * m). Все необходимые данные есть в условии и их необходимо просто подставить: ΔT = — 350 Вт * 15 с / 4200 Дж * 0,6 кг = — 2,1 С 0 . Минус в ответе показывает, что температура понижается. Задача решена.
Вот ещё одна задача, для решения которой необходимо вначале исследовать ситуацию. В ёмкость поместили смесь, состоящую из пяти килограммов воды и трёх килограммов льда. Затем туда пустили 0,2 кг водяного пара при температуре 100 0 С. Нужно определить, что произойдёт.
По условию задачи даны три массы mв, mл, mп. Можно предположить, что при смешении в момент запуска пара температура в системе была нулевой. Это исходит из того, что в ёмкости одновременно находится лёд и вода. Поступающий пар конденсирует, и из него образуется вода. Через время она остывает до нуля. Поэтому в начальный момент выделившаяся энергия идёт только на таяние льда. Cуществует три варианта развития события:
- Лёд не растает ( θ =0 0 С).
- Лёд полностью растает (0 0 С).
- Вода начнёт кипеть ( θ = 100 0 С) .
Для того чтобы выяснить, какой вариант верный, нужно найти выделившуюся энергию: Qпл = λ * m = 330 * 3 = 990 кДж. Получается, чтобы растопить лёд, нужно 990 кДж теплоты. Пар, вступая в реакцию, отдаёт: Q- = L* m + cв * mв (Tпар – Tпл) = 2300 + 0,2 + 4,2 * 0,2 * 100 = 544 кДж. Учитывая два полученных результата, можно утверждать, что при конденсации основного пара выделившейся теплоты будет недостаточно для расплавления льда. Следовательно θ = 0 0 С.
Видео:Урок 112 (осн). Уравнение теплового балансаСкачать

Фазовые переходы и уравнение теплового баланса
теория по физике 🧲 термодинамика
Фазовые переходы — это термодинамические процессы, приводящие к изменению агрегатного состояния вещества.
Видео:89 НЕ ЗНАЮТ этого в Физике: Что такое Количество Теплоты, Теплоемкость, Уравнение Теплового БалансаСкачать

Плавление и отвердевание
Для расчета количества теплоты, необходимого для процесса плавления, следует применять формулу:
m — масса вещества, λ (Дж/кг) — удельная теплота плавления.
Плавление каждого вещества происходит при определенной температуре, которую называют температурой плавления. Все проводимое тепло идет на разрушение кристаллической решетки, при этом увеличивается потенциальная энергия молекул. Кинетическая энергия остается без изменения и температура в процессе плавления не изменяется.
Удельная теплота плавления показывает, какое количество теплоты необходимо сообщить 1 кг данного вещества, чтобы перевести его из твердого состояния в жидкое при условии, что оно уже нагрето до температуры плавления. В процессе отвердевания 1 кг данной жидкости, охлажденной до температуры отвердевания, выделится такое же количество теплоты.
Внимание! Удельная теплота плавления — табличная величина.
Определение Отвердевание, или кристаллизация — переход состояния из жидкого состояния в твердое (это процесс, обратный плавлению).
Отвердевание происходит при той же температуре, что и плавление. В процессе отвердевания температура также не изменяется. Количество теплоты, выделяемое в процессе отвердевания:
Видео:Урок 113 (осн). Задачи на уравнение теплового балансаСкачать

Парообразование и конденсация
Количество теплоты, необходимое для процесса кипения, вычисляют по формуле:
m — масса вещества, r (Дж/кг) — удельная теплота парообразования.
Парообразование происходит при определенной температуре, которую называют температурой кипения. В отличие от испарения, процесс парообразования идет со всего объема жидкости. Несмотря на то, что к кипящему веществу подводят тепло, температура не изменяется. Все затраты энергии идут на увеличение промежутком между молекулами. Температура кипения зависит от рода вещества и внешнего атмосферного давления.
Удельная теплота парообразования показывает, какое количество теплоты необходимо затратить, чтобы перевести в пар 1 кг жидкости, нагретой до температуры кипения. Такое же количество теплоты выделится в процессе конденсации 1 кг пара, охлажденного до температуры конденсации.
Внимание! Удельная теплота парообразования — табличная величина.
Определение Конденсация — процесс, обратный кипению. Это переход вещества из газообразного состояния в жидкое.
Конденсация происходит при температуре кипения, которая также не изменяется во время всего процесса. Количество теплоты, выделяемое в процессе конденсации:
Видео:Уравнение теплового балансаСкачать

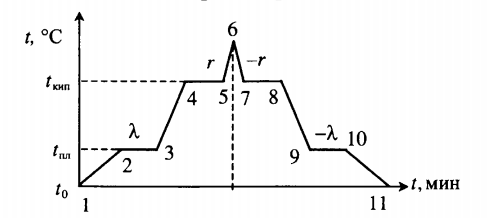
Тепловые процессы при нагревании и охлаждении
Все фазовые переходы, а также процессы нагревания и остывания вещества можно отобразить графически. Посмотрите на график фазовых переходов вещества:
Он показывает зависимость температуры вещества от времени в процессе его нагревания и остывания. Опишем процессы, отображаемые на графике, в таблице.
| Процесс | Что происходит | Количество выделенной теплоты | ||||||||||||||||||||||||||||||||||||||||||||||||
| 1–2 | Нагревание твердого тела | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2–3 | Плавление при температуре плавления (tпл) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 3–4 | Нагревание жидкости | |||||||||||||||||||||||||||||||||||||||||||||||||
| 4–5 | Кипение при температуре кипения (tкип) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 5–6 | Нагревание пара | |||||||||||||||||||||||||||||||||||||||||||||||||
| 6–7 | Охлаждение пара | |||||||||||||||||||||||||||||||||||||||||||||||||
| 7–8 | Кипение при температуре кипения (tкип) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 8–9 | Охлаждение жидкости | |||||||||||||||||||||||||||||||||||||||||||||||||
| 9–10 | Отвердевание при температуре плавления (tпл) | |||||||||||||||||||||||||||||||||||||||||||||||||
| 10–11 | Охлаждение твердого тела |
| Что происходит | График | Формула количества теплоты | |||||||||||||||||||||||||||||||||||||
| Полностью растопили лед, имеющий отрицательную температуру. | 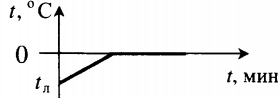 | ||||||||||||||||||||||||||||||||||||||
| Лед, взятый при отрицательной температуре, превратили в воду при комнатной температуре. | 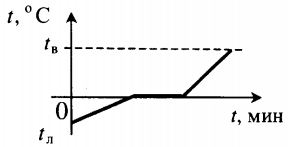 | ||||||||||||||||||||||||||||||||||||||
| Взяли лед при температуре 0 о С и полностью испарили. | 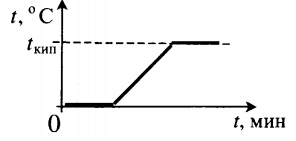 | ||||||||||||||||||||||||||||||||||||||
| Взяли воду при комнатной температуре и половину превратили в пар. | 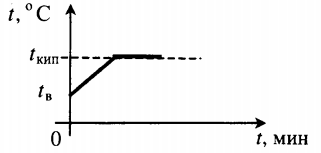 |
| Единицы измерения | Температуру можно оставлять в градусах Цельсия, так как изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах. |
| Кипяток | Вода, которая при нормальном атмосферном давлении имеет температуру в 100 о С. |
| Объем воды 5 л | m = 5 кг, так как: m = ρ V =10 3 · 5 · 10 − 3 м 3 = 5 к г Внимание! Равенство V (л) = m (кг) справедливо только для воды. |
Пример №1. Какое количество теплоты нужно сообщить льду массой 2 кг, находящемуся при температуре –10 о С, чтобы превратить его в воду и нагреть ее до температуры +30 о С?
Можно выделить три тепловых процесса:
- Нагревание льда до температуры плавления.
- Плавление льда.
- Нагревание воды до указанной температуры.
Поэтому количество теплоты будет равно сумме количеств теплоты для каждого из этих процессов:
Q = Q 1 + Q 2 + Q 3
Q = c л m ( 0 − t 1 ) + λ m + c в m ( t 2 − 0 )
Удельные теплоемкости и удельную теплоту плавления смотрим в таблицах:
- Удельная теплоемкость льда = 2050 Дж/(кг∙К).
- Удельная теплоемкость воды = 4200 Дж/(кг∙К).
- Удельная теплота плавления льда = 333,5∙10 3 Дж/кг.
Q = 2050 · 2 ( 0 − ( − 10 ) ) + 333 , 5 · 10 3 · 2 + 4220 · 2 · 30 = 961200 ( д ж ) = 961 , 2 ( к Д ж )
Видео:Урок 127 (осн). Задачи на уравнение теплового баланса - 1Скачать

Уравнение теплового баланса
Суммарное количество теплоты, которое выделяется в теплоизолированной системе равно количеству теплоты (суммарному), которое в этой системе поглощается.
Математически уравнение теплового баланса с учетом знаков количества теплоты записывается так:
Q о т д = − Q п о л
Отданное количество теплоты меньше нуля (Qотд 0).
Подсказки к задачам на уравнение теплового баланса
| Теплообмен происходит в калориметре | Потерями энергии можно пренебречь. |
| Жидкость нагревают в некотором сосуде | Начальные и конечные температуры жидкости и сосуда совпадают. |
| В жидкость опускают термометр | Через некоторое время он покажет конечную температуру жидкости и термометра. |
| Мокрый снег | Содержит воду и лед при 0 о С. Учтите, что лед плавится, если он находится при температуре 0 о С и получает энергию от более нагретого тела. Вода кристаллизируется при температуре 0 о С, если она отдает энергию более холодному телу. Если лед и вода находятся при температуре 0 о С, то никаких агрегатных переходов между ними не происходит. |
Частные случаи теплообмена
| В воду комнатной температуры бросили ком снега, содержащий некоторое количество воды, после чего установилась некоторая положительная температура. | 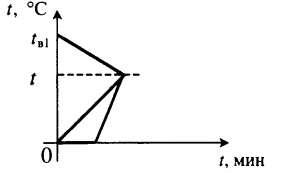 Уравнение теплового баланса: Уравнение теплового баланса:Q 1 + Q 2 + Q 3 = 0 c в m в 1 ( t − t в 1 ) + c в m в 2 ( t − 0 ) + λ m л + c в m л ( t − 0 ) = 0 | ||||||||||||||
| Для получения некоторой положительной температуры воды используют горячую воду и лед, имеющий отрицательную температуру. | 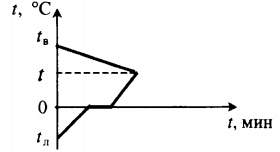 Уравнение теплового баланса: Уравнение теплового баланса:c в m в ( t − t в ) + c л m л ( 0 − t л ) + λ m л + c в m л ( t − 0 ) = 0 | ||||||||||||||
| В воду комнатной температуры бросают раскаленное твердое тело, в результате часть воды испаряется. | 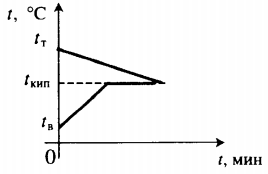 Уравнение теплового баланса: Уравнение теплового баланса:c т m т ( 100 − t т ) + c в m в ( 100 − t в ) + r m п = 0 | ||||||||||||||
| Воду комнатной температуры нагревают до кипения, вводя пар при t = 100 о С. | 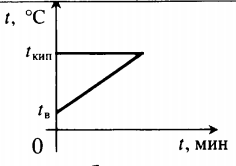 Уравнение теплового баланса: Уравнение теплового баланса:− r m п + c в m в ( 100 − t в ) = 0 | ||||||||||||||
| Лед, имеющий температуру плавления, нагревают до положительной температуры, вводя пар при t = 100 о С. | 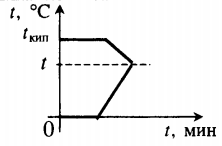 Уравнение теплового баланса: Уравнение теплового баланса:− r m п + c в m п ( t − t к и п ) + λ m л + c в m л ( t − t п л ) = 0 Пример №2. В кастрюлю, где находится вода объемом 2 л при температуре 25 о С, долили 3 л кипятка. Какая температура воды установилась? Количество теплоты, отданное кипятком, равно количеству теплоты, принятому более прохладной водой. Поэтому: c m 1 ( t − t 0 ) = − c m 2 ( t − t к и п ) m 1 ( t − t 0 ) = − m 2 ( t − t к и п ) m 1 t + m 2 t = m 1 t 0 + m 2 t к и п ( m 1 + m 2 ) t = m 1 t 0 + m 2 t к и п t = m 1 t 0 + m 2 t к и п m 1 + m 2 . . t = 2 · 25 + 3 · 100 2 + 3 . . = 350 5 . . = 70 ( ° C ) Видео:Формы записи уравнения теплового балансаСкачать  Взаимные превращения механической и внутренней энергииЕсли в тексте задачи указан процент одного вида энергии, перешедший в другой, то он указывается в виде десятичной дроби перед этой энергией, которой тело обладало вначале. Частные случаи закона сохранения энергии
|







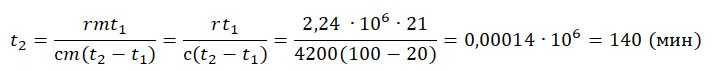
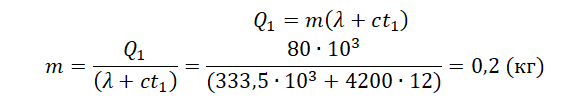
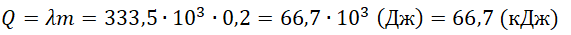
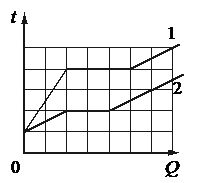 На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.
На рисунке представлены графики зависимости температуры t двух тел одинаковой массы от сообщённого им количества теплоты Q. Первоначально тела находились в твёрдом агрегатном состоянии.



 или
или  .
. , Сльда, водяного пара = 2100
, Сльда, водяного пара = 2100 . Теплоемкость тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть его на 1 С (или сколько энергии выделяет это тело, остывая на 1 С).
. Теплоемкость тела показывает, сколько энергии нужно подвести к данному телу, чтобы нагреть его на 1 С (или сколько энергии выделяет это тело, остывая на 1 С). .
. 1 = 0,1 кг
1 = 0,1 кг – ?
– ?




 . Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.
. Не трудно догадаться, что в результате теплообмена самая горячая пластина остынет, а самая холодная нагреется. Итак, мы знаем, что будет происходить с железной и алюминиевой пластинами: железная будет остывать, алюминиевая – нагреваться.
 1 = Q 2‘+ Q 3‘,
1 = Q 2‘+ Q 3‘,


 4 = 0 о С
4 = 0 о С


 1 = 3 кг
1 = 3 кг ,
,


 3 = 0,4 кг
3 = 0,4 кг



 ( 2 = 0,75)
( 2 = 0,75) 2 m 2 (t 2 ) = m 1 ( t 2 ),
2 m 2 (t 2 ) = m 1 ( t 2 ),

 ,
,
 1 = 1 кг
1 = 1 кг .
. ,
, .
.
 1 = 0,8 кг
1 = 0,8 кг

 .
.


 , где m — масса превратившейся в пар воды.
, где m — масса превратившейся в пар воды.
 1 = 0,8 кг
1 = 0,8 кг , m в , m л – ?
, m в , m л – ? 1 m 1( t 1 0) + m = c 2 m 2( t 2), где m масса превратившейся в лед воды.
1 m 1( t 1 0) + m = c 2 m 2( t 2), где m масса превратившейся в лед воды.
 . Лёд нагреется от 30 С до 0 С, расплавится, и образовавшаяся из льда вода нагреется от 0 С до температуры . А вода массой m 1 при этом остынет от 20 С до температуры . Тогда в калориметре будет находиться вода при температуре . Уравнение теплового баланса запишется так:
. Лёд нагреется от 30 С до 0 С, расплавится, и образовавшаяся из льда вода нагреется от 0 С до температуры . А вода массой m 1 при этом остынет от 20 С до температуры . Тогда в калориметре будет находиться вода при температуре . Уравнение теплового баланса запишется так: .
.
 ) = 0,116 (кг) = 116 (г)
) = 0,116 (кг) = 116 (г) ;
; .
. 1 = 12 С
1 = 12 С ;
; = 60 (л),
= 60 (л), .
. 1 = 2 кг
1 = 2 кг .
. = 2640 (Дж/ 0 С)
= 2640 (Дж/ 0 С) .
.
 ,
,