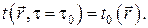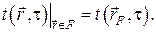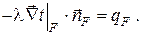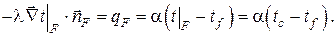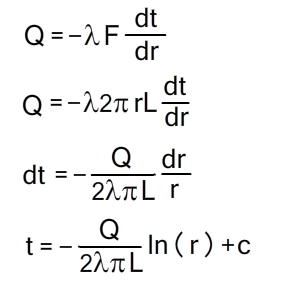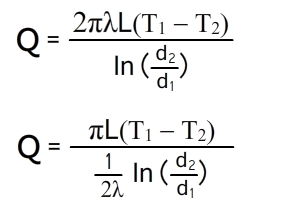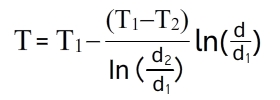Уравнение теплопроводности с граничными условиями первого рода (7 видео)

Лекция 4. Вывод уравнения теплопроводности

При построении математической модели распространения тепла в стержне сделаем следующие предположения:
1) стержень сделан из однородного проводящего материала с плотностью ρ;
2) боковая поверхность стержня теплоизолирована, то есть тепло может распространяться только вдоль оси ОХ;
3) стержень тонкий — это значит, что температура во всех точках любого поперечного сечения стержня одна и та же.

Рассмотрим часть стержня на отрезке [х, х + ∆х] (см. рис. 6) и воспользуемся законом сохранения количества тепла:

Общее количество тепла на отрезке [х, х + ∆х] = полному количеству тепла, прошедшему через границы + полное количество тепла, образованного внутренними источниками.

Общее количество тепла, которое необходимо сообщить участку стержня, чтобы повысить его температуру на ∆U, вычисляется по формуле: ∆Q= CρS∆x∆U, где С — удельная теплоемкость материала ( = количеству тепла, которое нужно сообщить 1 кг вещества, чтобы поднять его температуру на 1°), S — площадь поперечного сечения.

Количество тепла, прошедшее через левый конец участка стержня за время ∆t (тепловой поток) вычисляется по формуле: Q₁ = -kSU_x(x, t)∆t, где k — коэффициент теплопроводности материала ( = количеству тепла, протекающего в секунду через стержень единичной длины и единичной площади поперечного сечения при разности температур на противоположных концах, равной 1°). В этой формуле особого пояснения требует знак минус. Дело в том, что поток считается положительным, если он направлен в сторону увеличения х, а это, в свою очередь, означает, что слева от точки х температура больше, чем справа, то есть U_x CpS∆x∆U = kSU_x(x + ∆х, t) ∆t — kSU_x(x, t)∆t.

Если это равенство поделить на S∆x∆t и устремить ∆х и ∆t к нулю, то будем иметь:

Отсюда уравнение теплопроводности имеет вид

U_t = a 2 U_xx,
где 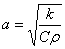— коэффициент температуропроводности.

В случае, когда внутри стержня имеются источники тепла, непрерывно распределенные с плотностью q(x,t), получится неоднородное уравнение теплопроводности

Содержание

Начальные условия и граничные условия.
Решение первой начально-краевой задачи для уравнения теплопроводности.
Краевые условия для уравнения теплопроводности
Теплопроводность через стенку
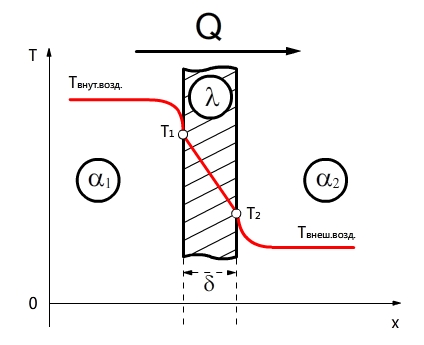
Теплопередача через плоскую стенку (граничные условия первого рода)
Распределение температуры в плоской стенке
Теплопроводность через многослойную стенку
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
📹 Видео

Начальные условия и граничные условия.

Для уравнения теплопроводности задается только одно начальное условие U|_t=0 = φ(х) (или в другой записи U(x,0) = φ(х)) и физически оно означает, что начальное распределение температуры стержня имеет вид φ(х). Для уравнений теплопроводности на плоскости или в пространстве начальное условие имеет такой же вид, только функция φ будет зависеть, соответственно, от двух или трех переменных.

Граничные условия в случае уравнения теплопроводности имеют такой же вид, как и для волнового уравнения, но физический смысл их уже иной. Условия первого рода (5) означают, что на концах стержня задана температура. Если она не изменяется со временем, то g₁(t) ≡ Т₁ и g₂(t) ≡ Т₂, где Т₁ и Т₂ — постоянные. Если концы поддерживаются все время при нулевой температуре, то Т₁= Т₂ = 0 и условия будут однородными. Граничные условия второго рода (6) определяют тепловой поток на концах стержня. В частности, если g₁(t) = g₂(t) = 0, то условия становятся однородными. Физически они означают, что через концы не происходит теплообмен с внешней средой (эти условия еще называют условиями теплоизоляции концов). Наконец, граничные условия третьего рода (7) соответствуют случаю, когда через концы стержня происходит теплообмен с окружающей средой по закону Ньютона (напомним, что при выводе уравнения теплопроводности мы считали боковую поверхность теплоизолированной). Правда, в случае уравнения теплопроводности условия (7) записываются немного по-другому:

Физический закон теплообмена со средой (закон Ньютона) состоит в том, что поток тепла через единицу поверхности в единицу времени пропорционален разности температур тела и окружающей среды. Таким образом, для левого конца стержня он равен Здесь h₁ > 0 — коэффициент теплообмена с окружающей средой, g₁(t) — температура окружающей среды на левом конце. Знак минус поставлен в формуле по той же причине, что и при выводе уравнения теплопроводности. С другой стороны, в силу теплопроводности материала поток тепла через этот же конец равен Применив закон сохранения количества тепла, получим:

Аналогично получается условие (14) на правом конце стержня, только постоянная λ₂ может быть другой, так как, вообще говоря, среды, окружающие левый и правый конец, бывают разные.

Граничные условия (14) являются более общими по сравнению с условиями первого и второго рода. Если предположить, что через какой-либо конец не происходит теплообмена со средой (то есть коэффициент теплообмена равен нулю), то получится условие второго рода. В другом случае предположим, что коэффициент теплообмена, например h₁, очень большой.

Перепишем условие (14) при х = 0 в виде и устремим . В результате будем иметь условие первого рода:

Аналогично формулируются граничные условия и для большего числа переменных. Для задачи о распространении тепла в плоской пластине условие означает, что температура на ее краях поддерживается нулевой. Точно так же, условия и внешне очень похожи, но в первом случае оно означает, что рассматривается плоская пластина и края ее теплоизолированы, а во втором случае оно означает, что рассматривается задача о распространении тепла в теле и поверхность его теплоизолирована.

Решение первой начально-краевой задачи для уравнения теплопроводности.

Рассмотрим однородную первую начально-краевую задачу для уравнения теплопроводности:

Найти решение уравнения

удолетворяющее граничным условиям

и начальному условию

Решим эту задачу методом Фурье.

Шаг 1. Будем искать решения уравнения (15) в виде U(x,t) = X(x)T(t).

Найдем частные производные:

Подставим эти производные в уравнение и разделим переменные:

По основной лемме получим

Теперь можно решить каждое из этих обыкновенных дифференциальных уравнений. Обратим внимание на то, что используя граничные условия (16), можно искать не общее решение уравнения б), а частные решения, удолетворяющие соответствующим граничным условиям:

Шаг 2. Решим задачу Штурма-Лиувилля

Эта задача совпадает с задачей Штурма-Лиувилля, рассмотренной в лекции 3. Напомним, что собственные значения и собственные функции этой задачи существуют только при λ>0.

Собственные значения равны

Собственные функции равны (См. решение задачи)

Шаг 3. Подставим собственные значения в уравнение а) и решим его:

Шаг 4. Выпишем частные решения уравнения (15):

В силу линейности и однородности уравнения (15) их линейная комбинация

Шаг 5. Определим коэффициенты A_n в (19), используя начальное условие (17):

Приходим к тому, что начальная функция φ(x) разлагается в ряд Фурье по собственным функциям задачи Штурма-Лиувилля. По теореме Стеклова такое разложение возможно для функций, удовлетворяющих граничным условиям и имеющих непрерывные производные второго порядка. Коэффициенты Фурье находятся по формулам

Вычислив эти коэффициенты для конкретной начальной функции φ(x) и подставив их значения в формулу (19), мы тем самым получим решение задачи (15), (16), (17).

Замечание. Используя формулу (19), можно также, как в лекции 3, получить решение первой начально-краевой задачи для уравнения U_t = a 2 U_xx. Оно будет иметь вид

где

Видео:Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать

Краевые условия для уравнения теплопроводности

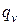
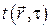
Дифференциальное уравнение теплопроводности в однородных изотропных средах в терминах математической физики есть неоднородное дифференциальное уравнение в частных производных параболического типа (первого порядка по времени и второго порядка по пространственным координатам). Если внутренние тепловыделения зависят от температуры

, то уравнение теплопроводности будет нелинейным, если плотность внутренних источников теплоты зависит от температуры нелинейным образом. Если же плотность внутренних источников теплоты пропорциональна первой степени температуры или не зависит от температуры, то уравнение теплопроводности будет либо линейным, либо квазилинейным, оставаясь, тем не менее, уравнением параболического типа.

Как бы то ни было, любое дифференциальное уравнение может дать однозначное решение только если заданы условия однозначности. В случае дифференциального уравнения параболического типа должно быть задано начальное условие

Что касается граничных условий, то-есть условий теплообмена на границе рассматриваемого объёма с окружающей (контактирующей с ним) средой, то здесь имеют место несколько (а именно, четыре) возможностей, каждая из которых характеризует тот или иной тип теплового взаимодействия с внешней средой. Эти возможности обычно нумеруются римскими цифрами. Перечислим их.

I. Граничные условия I рода

В этом случае задаётся распределение температур на физической границе рассматриваемого объёма, т.е. задаётся функция координат поверхности и времени

II. Граничные условия II рода

Задаётся плотность теплового потока на границе рассматриваемого тела, что позволяет записать

Такие граничные условия обычно имеют место при решении задач теплопроводности в твёрдых телах с теплообменом излучением на границах. Чаще всего такие задачи возникают при решении задач в металлургической теплотехнике, в астрофизике и т.д.

III. Граничные условия III рода

Граничные условия III рода наиболее распространены при решении задач теплопроводности в энергетике, в металлургии и в химической технологии.

Граничные условия III рода описывают в математической форме условия теплообмена внешней поверхности твёрдого тела с контактирующей с ним жидкостью или газом, т.е. со средами, допускающими конвективные движения с перемешиванием.

Математическая формулировка граничных условий III рода базируется на гипотезе (законе) Ньютона-Рихмана, согласно которой тепловой поток с поверхности к омывающей её жидкости пропорционален разности температур, т.е.

Здесь 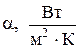есть по определению коэффициент теплоотдачи, представляющий собой количество теплоты, снимаемое в единицу времени с единичной поверхности при единичной разности температур.

Экспериментальное обоснование гипотезы Ньютона-Рихмана состоит в том, что, как показывают экспериментальные исследования, количество теплоты, снимаемое с поверхности твёрдого тела, прямо пропорционально поверхности и разности температур поверхности и жидкости вдали от неё (как говорят, в ядре потока). Нахождение величины коэффициента теплоотдачи 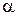является задачей экспериментальной теплофизики (вплоть до теоретических исследований) и будет обсуждено в дальнейшем изложении курса. В задачах теплопроводности значения коэффициентов теплоотдачи будут считаться заданными и постоянными.

IV. Граничные условия IV рода

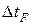
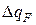
Граничные условия IV рода задают условия теплообмена на границе контакта твёрдых поверхностей. В частности, если контакт твёрдых поверхностей неидеален, то на границе их контакта в математическом смысле будет иметь место скачок температуры , а при наличии тепловыделения на поверхностях контакта будет иметь место дополнительный поток тепла . В этом случае граничные условия математически запишутся в виде

Видео:Решение уравнения теплопроводности / граничные условия второго и третьего родаСкачать

Теплопроводность через стенку

Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.

Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача — величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической — по логарифмическому закону, т.е.

Q = const и T = f(x) — линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).

Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.

Теплопередача через непроницаемую стенку включает в себя следующие процессы:

теплоотдачу от горячей среды к стенке;
теплопроводность внутри стенки;
теплоотдачу от стенки к холодной среде.

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

Теплопередача через плоскую стенку (граничные условия первого рода)

Теплопроводность — первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.

Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.

Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.

Тепловой поток Q [Вт] — это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).

Поверхностная плотность теплового потока рассчитывается по формуле:

где Q — тепловой поток [Вт]; F — площадь стенки [м 2 ].

На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:

где δ = dx — толщина стенки, λ

λ/δ; [Вт/м 2 *К] — коэфициент тепловой проводности стенки.

а обратная величина —

R = δ/λ; [м 2. К/Вт] — термическое сопротивление стенки.

Для теплового потока формулу так же можно представить в виде:

Общее количество теплоты проходящее через площадь стены S за время t можно представить как:

Видео:6-1. Уравнение теплопроводностиСкачать

Распределение температуры в плоской стенке

Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C₁; T=C₁х+С₂ (1). Определим С₁ и С₂ через граничные условия.

При х=0 T=T₁, подставим в уравнение (1) и получим T₁=С₂.
При х=δ T=T₂, подставим в уравнение (1) и получим T₂=С₁*δ+С₂, T₂=С₁*δ+T₁, получим: С₁=(Т₂-T₁)/δ. Теперь подставим в уравнение (1) найденные С₁ и С₂, получим следующее распределение температуры в нашей стене:

Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:

Видео:Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать

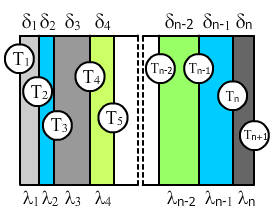
Теплопроводность через многослойную стенку

Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λ_i и разной толщиной δ_i.

Термическое сопротивление стенки считается так:

Для теплового потока формула будет иметь вид:

Температура на границе слоя вычисляется по следующей формуле:

Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:

Эквивалентная теплопроводность многослойной стенки:

Видео:Решение уравнения теплопроводности методом конечных разностейСкачать

Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)

Теплопередача — это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.

Коэффициент теплоотдачи α, Вт/(м 2 ·К) — это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.

Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:

q = k * (T_{возд.внутри} — T_{возд.снаружи}); Вт/м 2

Коэффициент теплопередачи для n слойной стенки:

Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:

Тогда общее термическое сопротивление теплопередаче будет равно:

Температуры на поверхности стенки можно определить по формулам:

Видео:Закон и уравнение теплопроводностиСкачать

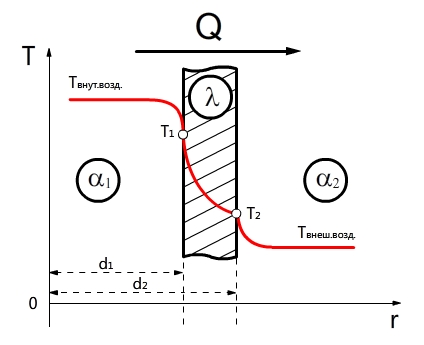
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)

Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа «труба в трубе», кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.

Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:

Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы принимают следующий вид:

Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.

Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.

Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.

Сайт может содержать контент, запрещенный для просмотра лицам до 18 лет.