Уравнения Максвелла — это 4 уравнения, которые описывают, как электрические и магнитные поля распространяются и взаимодействуют; т.е. эти уравнения (правила или даже законы) описывают процессы/взаимодействия электромагнетизма.
Эти правила описывают, как проходит управление поведением электрических и магнитных полей. Уравнения Максвелла показывают, что электрический заряд (положительный и отрицательный):
- Порождает электрическое поле (также если заряд изменяется со временем, то он вызывает появление электрического поля).
- В дальнейшем он вызывает появление магнитного поля.
- Уравнения Максвелла в дифференциальной форме
- Уравнение 1: Закон Гаусса или Теорема Гаусса
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- Уравнения Максвелла в интегральной и дифференциальной форме
- Уравнение 1: Закон Гаусса (Теорема Гаусса)
- Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
- Уравнение 3: Закон Гаусса для магнетизма
- Уравнение 4: Закон Ампера
- 2.6. Электромагнитные волны
- Связь между электрическим и магнитным полями
- 📹 Видео
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Уравнения Максвелла в дифференциальной форме
Уравнение 1: Закон Гаусса или Теорема Гаусса
Дивергенция электрического поля равняется плотности заряда. Существует вязь между электрическим полем и электрическим зарядом.
Дивергенция в физике показывает, насколько данная точка пространства является источником или потребителем потока поля.
Очень кратко: Электрические поля расходятся от электрических зарядов: электрический заряд создаёт поле вокруг себя и, таким образом, действует как источник электрических полей. Это можно сравнить с краном, который является источником воды.
Ещё закон Гаусса говорит о том, что отрицательные заряды действуют как сток для электрических полей (способ, как вода стекает через отверстие стока). Это означает, что линии электрического поля имеют начало и поглощаются при электрическом заряде.
Заряды с одинаковым знаком отталкиваются друг от друга, а противоположные заряды притягиваются друг к другу (если есть два положительных заряда, они будут отталкиваться; а если есть один отрицательный и один положительный, они будут притягиваться друг к другу).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
Можно создать электрическое поле, изменив магнитное поле.
Очень кратко: Закон Фарадея гласит, что изменяющееся магнитное поле внутри контура вызывает индуцированный ток, который возникает из-за силы или напряжения внутри контура. Это значит:
- Электрический ток порождает магнитные поля, а эти магнитные поля (вокруг цепи) вызывают электрический ток.
- Изменяющееся во времени магнитное поле вызывает распространение электрического поля.
- Циркулирующее во времени электрическое поле вызывает изменение магнитного поля во времени.
Уравнение 3: Закон Гаусса для магнетизма
Дивергенция магнитного потока любой замкнутой поверхности равна нулю. Магнитного монополя не существует.
Закон Гаусса для магнетизма утверждает (очень кратко):
- Магнитных монополей не существует.
- Расхождение полей B или H всегда равно нулю в любом объёме.
- На расстоянии от магнитных диполей (это круговой ток) магнитные поля текут по замкнутому контуру.
Уравнение 4: Закон Ампера
Магнитное поле создаётся с помощью тока или изменяющегося электрического поля.
Очень кратко: Электрический ток порождает магнитное поле вокруг тока. Изменяющийся во времени электрический поток порождает магнитное поле.
Видео:1.1 Векторы напряженности и индукции электрического и магнитного полейСкачать

Уравнения Максвелла в интегральной и дифференциальной форме
Вспомним сначала в дифференциальной форме и следом будет в интегральной форме.
Уравнение 1: Закон Гаусса (Теорема Гаусса)
Это же уравнение в интегральной форме:
Поток вектора электрической индукции D через любую замкнутую поверхность равняется сумме свободных зарядов, охваченных этой поверхностью. Электрическое поле создаётся нескомпенсированными электрическими зарядами (это те, что создают вокруг себя своё собственное электрическое поле).
Уравнение 2: Закон электромагнитной индукции (Закон Фарадея)
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Е вихревого электрического поля (по любому замкнутому контуру) равняется скорости изменения магнитного потока через площадь контура (S) с противоположным знаком.
Уравнение 3: Закон Гаусса для магнетизма
И это же уравнение в интегральной форме:
Силовые линии магнитного поля замкнуты, т.к. поток вектора индукции В магнитного поля через любую замкнутую поверхность равняется нулю.
Уравнение 4: Закон Ампера
И это же уравнение в интегральной форме:
Циркуляция вектора напряжённости Н магнитного поля по замкнутому контуру равняется алгебраической сумме токов, которые пронизывают этот контур. Магнитное поле создаётся не только током проводимости, но и переменным электрическим полем.
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

2.6. Электромагнитные волны
Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды (
Величины 

Постоянные 

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.
Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.
Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.
При строго гармоническом изменении во времени векторов 

Получим из уравнений Максвелла волновые уравнения для векторов 

Волновое уравнение для электромагнитных волн
Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.
Возьмем ротор от обеих частей уравнения
При этом воспользуемся доказываемой в курсе математики формулой:
где 
Получаем в итоге:
Выразим rotB через электрическое поле с помощью уравнения Максвелла:
и используем это выражение в правой части (2.93). В результате приходим к уравнению:
и вводя показатель преломления среды
запишем уравнение для вектора напряженности электрического поля в виде:
Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:
Взяв ротор от обеих частей уравнения Максвелла
и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:
Полученные волновые уравнения для 

В отсутствие среды (при 
Основные свойства электромагнитных волн
Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:
Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:
Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:
Дифференцирование плоских волн по времени дает:
Тогда из уравнений Максвелла следует:
Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:
Далее, ни у 

Иными словами и в изотропной среде,
электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.
Тогда можно выбрать координатные оси так, чтобы вектор 
Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне
В этом случае уравнения (2.103) приобретают вид:
Отсюда следует, что вектор 
Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:
Отсюда вытекает обычная связь волнового вектора, частоты и скорости:
а также связь амплитуд колебаний полей:
Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.
Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.
Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).
На рис. 2.28 представлена шкала электромагнитных волн.
Рис. 2.28. Шкала электромагнитных волн
Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.
Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.
http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.
http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».
http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.
http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.
Эффект Доплера для электромагнитных волн
Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:
Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:
Подставим эти выражения в выражение для фазы 

Это выражение можно записать как
где 

Для электромагнитной волны в вакууме
Пусть направление распространения волны составляет в первой системе отсчета угол 
Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:
Это и есть формула Доплера для электромагнитных волн.
Если 
Если 
При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E0 вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H0 и вектора магнитной индукции B0 в волне.
Ответ находим сразу из уравнений (3.127), где полагаем 
Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:
Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время 

На площадку действует со стороны волны сила
Давление Р, оказываемое волной, равно
Если средняя плотность энергии в волне равна , то на площадь А за время 

Отсюда находим давление электромагнитной волны (света):
Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.
Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:
Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.
Видео:Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Связь между электрическим и магнитным полями
Билет№1.
1. Материальность электромагнитного поля (ЭМП).
Взаимосвязь электрического и магнитного полей обусловливает распространение электромагнитного поля в пространстве. Представим себе, что по проводнику течет переменный электрический ток. Тогда вокруг этого проводника существует переменное магнитное поле В (рис. 126). Это поле, в свою очередь, создает переменное электрическое поле Е в соседних участках пространства. Затем переменное электрическое поле порождает переменное магнитное поле, которое снова вызывает появление переменного электрического поля и т.д.. Итак, распространяясь на все новые участки пространства, электромагнитное поле перемещается из областей, где оно только существовало. Скорость распространения электромагнитного поля равна примерно 300 000 км / с.
Таким образом, электромагнитное поле может существовать самостоятельно, не будучи связанным с зарядами и токами. А это является убедительным доказательством материальности электромагнитного поля. В материальности электромагнитного поля убеждает и тот факт, что оно имеет определенную энергию. Распространение в пространстве электромагнитного поля, в котором напряженность электрического и индукция магнитного полей изменяются периодически, называется электромагнитной волной. Векторы напряженности Е и магнитной индукции В в электромагнитной волне в любой точке пространства всегда взаимно перпендикулярны, так как линии напряженности электрического поля охватывают линии индукции магнитного поля.
В 1865 г. Максвелл теоретически предсказал существование электромагнитных волн, открытых впоследствии Герцем. Из теории Максвелла следовало, что свет имеет электромагнитную природу — это электромагнитные волны с длиной около 10 -7 м. Максвелл показал, что электромагнитная волна переносит определенную энергию, при падении на препятствие она должна оказывать давление. Теория позволяла, в частности, вычислить давление света на поглощающую или отражающую поверхность.
Давление электромагнитных волн означает, что электромагнитное поле переносит вместе с энергией определенный импульс. Электромагнитная волна может оказывать и вращающее действие на препятствие. Все это доказательства материальности электромагнитного поля.
2. Электростатическое экранирование.
Если в электрическое поле внести проводник, то в результате поляризации электроны в нем начнут перемещаться в сторону положительно заряженной пластины и на части проводника, обращенной к этой пластине, возникает отрицательный потенциал, а противоположная часть поверхности проводника окажется заряженной положительно. Положительная и отрицательная части проводника создают свое собственное вторичное поле, которое равно внешнему и имеет направление противоположное ему.
Следовательно, внешнее электрическое поле и внутреннее поле создаваемое проводником, компенсируют друг друга во всех точках внутри тела проводника. Этим и объясняется распределение зарядов только на поверхности проводника.
Внутри проводника поле отсутствует (рис. 1).
Рис.1. Электрическое поле внутри проводника.
В самом деле, поскольку всюду внутри металлического тела поле равно нулю, то достаточно поместить в его внутренней полости устройство, подверженное влиянию электростатического поля и тем самым исключить влияние поля на это устройство. В этом случае эффективность экранирования оказывается независимой ни от формы экрана, ни от толщины его стенок, ни от металла, из которого он изготовлен.
Поместим заряд +q в центре сферической металлической оболочки (рис. 2).
Рис. 2. Заряд в центре металлической оболочки.
На внутренней поверхности оболочки возникают заряды –q, а на внешней — +q, и экран оказывается не эффективным. Однако, если теперь подключить металлическую оболочку к земле (к корпусу) (рис. 3), то это приведет к тому, что заряды, находящиеся на внешней поверхности оболочки, стекут на землю (корпус), т.к. он обладает очень большой емкостью, вне оболочки поле окажется равным нулю.
Рис. 3. Заземленная металлическая оболочка.
Таким образом электростатическое экранирование по существу сводится к замыканию электростатического поля на поверхность металлического экрана и отводу электрических зарядов на землю (рис.3).
Если между элементом А, создающим электрическое поле, и элементом Б, который необходимо защитить от этого поля, поместить экран Э, соединенный с землей, то этот экран будет перехватывать электрические силовые линии, защищая Б.
Заземление электростатического экрана является необходимым элементом при реализации электростатического экранирования. При этом заземлитель желательно выполнять короткими широкими шинами с малой индуктивностью. Применение металлических экранов позволяет практически полностью устранить влияние электростатического поля.
Основной задачей экранирования электрических полей является снижение емкостной связи между источником наводки и защищаемым устройством. Следовательно, эффективность экранирования определяется в основном отношением емкостной связи между источником наводки и защищаемым элементом до и после установки заземленного экрана. Поэтому любые действия, приводящие к снижению емкостной связи, увеличивают эффективность экранирования.
Билет 2
1. Векторы ЭМП и основные физические величины.
2. Стационарное электрическое поле постоянных токов. Основные уравнения
Билет 3
Связь между электрическим и магнитным полями
Согласно Максвеллу всякое изменение электрического поля порождает магнитное поле с замкнутыми силовыми линиями, охватывающими линии вектора Е и наоборот: всякое изменение магнитного поля порождает электрическое поле с замкнутыми силовыми, охватывающими линии вектора В. Таким образом, переменные электрическое и магнитное поля существуют всегда совместно, образуя единое электромагнитное поле. Взаимно порождая друг друга, электрическое и магнитное поля распространяются, образуя электромагнитные волны. Источником электромагнитных волн является переменный ток или ускоренное движение отдельных зарядов. Электромагнитные волны поперечные, т.к. в каждой точке пространства векторы Е и В, будучи перпендикулярны друг к другу, колеблются в направлениях, перпендикулярных к направлению распространения волны
2) Аналогия между полем в проводящей среде и электростатическим полем
. Электростатическое поле создается неподвижными и неизменными во времени зарядами, а поле в проводящей среде – это поле зарядов, имеющих упорядоченное движение под действием внешнего источника. Тем не менее между этими двумя полями может быть проведена формальная аналогия, которая заключается в следующем.
1.Электростатическое поле в областях, не занятых зарядом, и поле в проводящей среде в областях, свободных от источников ЭДС, описываются одним и тем же уравнением – уравнением Лапласа. Для электростатического поля мы уже показывали, что 







2. В каждом из этих полей могут быть найдены сходные величины, основные из которых указаны в табл.
| Электростатическое поле |  | j |  | ea |  |
| Поле в проводящей среде |  | j |  | g |  |

Билет 4
1. 1) Первое уравнение Максвелла в интегральной и дифференциальной формах.
E – векторное электрическое поле (здесь и далее жирным шрифтом выделены векторные величины, а курсивом — скалярные);
∇· – значок оператора дивергенции (потока);
ρ – суммарный заряд;
εo = 8,85418782. •10 -12 Ф/м – диэлектрическая постоянная вакуума, измеряется экспериментально по силе притяжения между зарядами.


2)Линии напряжённости поля и линии тока утечки в изоляции можно считать направленными по радиусам
Провндём внутри изоляции цилиндрическую поверхность имеющую радиус r и длину l в направлении оси кабеля. Имеем i=2пrl J и следовательно E=J/Y=i/2пrly
Напряжение Uab между проводами найдём сосавляя линейный интеграл напряженности электрического поля вдоль радиуса

Билет 5
1.Второе уравнение Максвелла— это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве

где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС. ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.

Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. То есть переменное магнитное поле возбуждает вихревое электрическое поле.
Получим второе уравнение Максвелла в интегральной форме
Уравнение 1.19 – второе уравнение Максвелла в интегральной форме.
Воспользуемся уравнением Стокса 1.13, преобразуем левую часть уравнения 1.19:
Уравнение 1.20 есть второе уравнение Максвелла в дифференциальной форме.
В изотропных средах
Подставим в уравнение 1.21, получим
Сопротивление заземления
Сопротивление заземления (сопротивление растеканиЮ электрического тока) определяется как величина «противодействия» растеканию электрического тока в земле, поступающего в нее через заземлитель.
Измеряется в Ом и должно иметь минимально низкое значение. Идеальный случай — нулевая величина, что означает отсутствие какого-либо сопротивления при пропускании «вредных» электротоков, что гарантирует их ПОЛНОЕ поглощение землей.
Так как идеала достигнуть невозможно, все электрооборудование и электроника создаются исходя из некоторых нормированных величин сопротивления заземления = 60, 30, 15, 10, 8, 4, 2, 1 и 0,5 Ом.
- для частных домов, с подключением к электросети 220 Вольт / 380 Вольт необходимо иметь локальное заземление с рекомендованным сопротивлением не более 30 Ом
При подключении локального заземления к нейтрали трансформатора / генератора в системе TN суммарное сопротивление заземления (локального + всех повторных + заземления трансформатора / генератора) должно быть не более 4 Ом (ПУЭ 1.7.101). Данное условие выполняется без каких-либо дополнительных мероприятий при правильном заземлении источника тока (трансформатора либо генератора)
Подробнее об этом на странице «Заземление дома».
- при подключении газопровода к дому должно выполняться стандартное требование для заземления дома. Однако из-за использования опасного оборудования необходимо выполнять локальное заземление с сопротивлением не более 10 Ом
(ПУЭ 1.7.103; для всех повторных заземлений)
Подробнее об этом на странице «Заземление газового котла / газопровода».
- для заземления, использующегося для подключения молниеприемников, сопротивление заземления должно быть не более 10 Ом (РД 34.21.122-87, п. 8)
Подробнее об этом на странице «Молниезащита и заземление».
- для источника тока (генератора или трансформатора) сопротивление заземления должно быть не более 2, 4 и 8 Омсоответственно при линейных напряжениях 660, 380 и 220 В источника трехфазного тока или 380, 220 и 127 В источника однофазного тока (ПУЭ 1.7.101)
- для уверенного срабатывания газовых разрядников в устройствах защиты воздушных линий связи (например, локальная сеть на основе медного кабеля или радиочастотный кабель) сопротивление заземления, к которому они (разрядники) подключаются должно быть не более 2 Ом. Встречаются экземпляры с требованием в 4 Ом.
- при подключении телекоммуникационного оборудования, заземление обычно должно иметь сопротивление
не более 2 или 4 Ом
- для подстанции 110 кВ сопротивление растеканию токов должно быть не более 0,5 Ом (ПУЭ 1.7.90)
Приведенные выше нормы сопротивления заземления справедливы для нормальных грунтов с удельным электрическим сопротивлением
не более 100 Ом*м (например, глина / суглинки).
Если грунт имеет более высокое удельное электрическое сопротивление — то часто (но не всегда) минимальные значения сопротивление заземления повышаются на величину 0,01 от удельного сопротивления грунта.
Например, при песчаных грунтах с удельным сопротивлением
500 Ом*м минимальное сопротивление локального заземления дома с системой TN-C-S повышается в 5 раз — до 150 Ом (вместо 30 Ом).
Расчет заземления (расчет сопротивления заземления) для одиночного глубинного заземлителя на основе модульного заземления 
Формула расчета сопротивления заземления одиночного вертикального заземлителя:

где:
ρ – удельное сопротивление грунта (Ом*м)
L – длина заземлителя (м)
d – диаметр заземлителя (м)
T — заглубление заземлителя (расстояние от поверхности земли до середины заземлителя) (м)
π — математическая константа Пи (3,141592)
ln — натуральный логарифм
Для готовых комплектов модульного заземления ZANDZ формула расчета сопротивления упрощается до вида:


где:
ρ – удельное сопротивление грунта (Ом*м)
Для расчета взяты следующие величины:
L = 15 (30) метров
d = 0,014 метра = 14 мм
T = 8 (15,5) метров: с учетом заглубления электрода на глубине 0,5 метра
БИЛЕТ 7
1.Принцип непрерывности магнитного потока в интегральной и дифференциальной формах: Основной физической величиной, характеризующей магнитное поле, является вектор магнитной индукции 
Для анализа магнитного поля в некоторой части пространства (рис.2.1) вводится понятие магнитного потока 




Поток вектора магнитной индукции сквозь некоторую поверхность s называют кратко магнитным потоком сквозь эту поверхность и обозначают через Ф
Магнитный поток измеряется в веберах (Вб).
📹 Видео
Билеты №32, 33 "Уравнения Максвелла"Скачать

Электрические и магнитные поляСкачать

Электрическое и магнитное поля. Занимательная физика.Скачать

Уравнения Максвелла в вакууме. Потенциалы электромагнитного поля.Скачать

60. Уравнения МаксвеллаСкачать

Как магнитное поле назвали магнитной индукциейСкачать

Раскрытие тайн электромагнитной волныСкачать

Лекция №9. Уравнения МаксвеллаСкачать

МАГНИТНОЕ ПОЛЕ за 24 минуты. ЕГЭ Физика. Николай Ньютон. ТехноскулСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
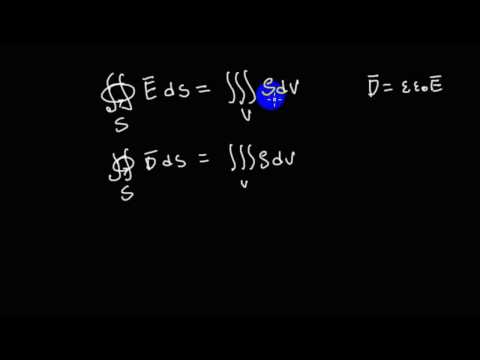
3 14 Уравнения МаксвеллаСкачать

Урок №45. Электромагнитные волны. Радиоволны.Скачать

Уравнения Максвелла Лекция 10-1Скачать

Математика это не ИсламСкачать

Система уравнений Максвелла. Связь интегральной и дифференциальной формы уравнений.Скачать

Вывод уравнения электромагнитной волныСкачать







































































