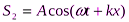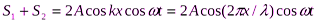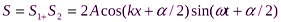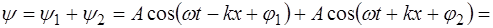Уравнение стоячей волны координаты узлов и пучностей (5 видео)

Уравнение стоячей волны координаты узлов и пучностей

§4 Интерференция волн.

Принцип суперпозиции. Понятие о когерентности волн

Если в среде распространяется несколько волн одновременно, то колебания частиц среды равны геометрической сумме колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются, не возмущая друг друга – принцип суперпозиции (наложения) волн.

Две волны называются когерентными, если разность их фаз не зависит от времени

—
условие когерентности.

Источники когерентных волн называются когерентными источниками.

т.к. для когерентных источников разность начальных фаз , то амплитуда А_резв различных точках зависит от величины , называемой разностью хода. Если

то наблюдается максимум.

При наложении волн от когерентных источников наблюдаются минимумы и максимумы, результирующей амплитуды, т.е. взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих, волн — суть явления интерференции.

§5 Стоячие волны

Частным случаем интерференции являются стоячие волны — волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу волн с одинаковыми амплитудами н частотами.

Для вывода уравнения стоячей волны примем: 1) волны распространяются в среде без затухания; 2) А₁ = А₂ =А — имеют равные амплитуды; 3) ω₁ = ω₂= ω — равные частоты; 4)φ₁₀ = φ₂₀ = 0.

Уравнение бегущей волны, распространяющейся вдоль положительного направления оси х (т.е. уравнение падающей волны):

(1)

Уравнение бегущей волны, распространяющейся в отрицательном направлении оси х (т.е. уравнение отраженной волны):

(2)

Сложив (1) и (2) получим уравнение стоячей волны:

Особенностью стоячей волны является то, что амплитуда зависит от координаты х. При перемещении от одной точки к другой амплитуда меняется по закону:

— амплитуда стоячей волны.

Те точки среды, в которых амплитуда стоячей волны максимальна и равна 2А, называются пучностями. Координаты пучностей можно найти из условия, что

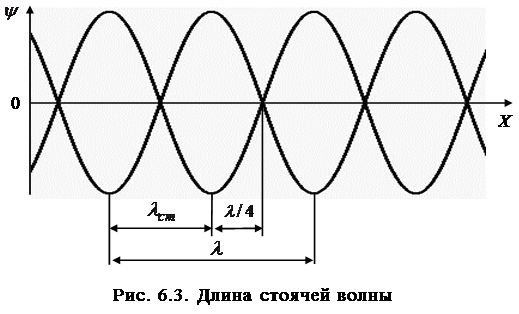
Расстояние между двумя соседними пучностями равно .

Точки, в которых амплитуда стоячей волны минимальна и равна 0 , называются узлами. Координата узлов можно найти из условия

Расстояние между двумя соседними узлами равно .

В отличие от бегущей волна, все точки которой колеблются с одинаковой амплитудой, но с разными фазами, зависящими от координаты х точки ( ), точки стоячей волны между двумя узлами колеблется с разными амплитудами, но с одинаковыми фазами( ). При переходе через узел множитель меняет свой знак, поэтому фаза колебаний по разные стороны от узла отличается на π, т.е. точки лежащие по разные стороны от узла колеблются в противофазе.

Стоячая волна получается в результате интерференции падающей и отраженной волн. На характере отражения сказывается граница раздела двух сред, от которой происходит отражение. Если волна отражается от среды менее плотной (рис. а), то фаза волны на границе раздела не меняется и на границе раздела двух сред будет пучность. Если волна отражается от более плотной среды, то её фаза изменяется на противоположную, т.е. отражение от более плотной среды происходит с потерей половины длины волны (λ/2). Бегущая волна переносит энергию колебательного движения в направлении распространения волны. Стоячая волна энергию не переносит, т.к. падаюшая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия результирующей стоячей волны, заключенной между узлами остается постоянной. Лишь в пределах расстояний равных λ/2 происходит превращение кинетической энергии в потенциальную.

Видео:«Стоячая волна» на экране осциллографаСкачать

Узлы стоячей волны

Стоячие волны

Волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.

Уравнение стоячей волны

(учли, что k = 2π/λ)—уравнение стоячей волны.

Пучности стоячей волны

Точки, в которых амплитуда максимальна (A_ст = 2Аcos(2πx/λ)) . Это точки среды, для которых

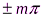
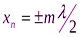
2πx/λ= (m=0,1,2,….)

(m = 0,1, 2. ).

Узлы стоячей волны

Точки, в которых амплитуда колебаний равна нулю (A_ст = 0). Это точки среды, для которых

(m = 0,1, 2. ).

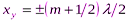
Расстояния пучность—пучность и узел—узел равны λ/2, а расстояние пучность—узел равно λ/4.

Образование стоячих волн наблюдают при

интерференции бегущей и отраженной волн. Например, если конец веревки закрепить неподвижно, то отраженная в месте закрепления веревки волна будет интерферировать с бегущей волной и образует стоячую волну. На границе, где происходит отражение волны, в данном случае получается узел. Будет ли на границе отражения узел или пучность, зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения получается пучность, если более плотная — узел. Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы происходит сложение колебаний противоположных направлений, в результате чего получается узел. Если волна отражается от менее плотной среды, то изменения фазы не происходит, и у границы колебания складываются с одинаковыми фазами — получается пучность.

Уравнение стоячей волны и его анализ

Частным случаем интерференции волн, являются стоячие волны.

Стоячей волной называется волна, образующаяся в результате наложения двух бегущих синусоидальных волн, которые распространяются навстречу друг другу и имеют одинаковые частоты и амплитуды, а в случае поперечных волн еще и одинаковую поляризацию.

Поперечная стоячая волна образуется, например, на натянутой упругой нити, один конец которой закреплен, а другой приводится в колебательное движение.

При наложении двух когерентных бегущих плоских волн вида

и где α-разность фаз волн в точках плоскости x=0, образуется плоская синусоидальная стоячая волна, описываемая уравнением

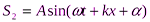
Амплитуда стоячей волны в отличие от амплитуды бегущих волн является периодической функцией координаты x.

Точки ,в которых амплитуда стоячей волны равна 0, называются узлами, а точки где амплитуда двойная –пучности.

Положение узлов и пучностей находится из условий

k*x+α/2=m*n (пучности) ,где m=0,1,2…

Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн.

В бегущей волне фаза колебаний зависит от координаты x рассматриваемой точки. В стоячей волне все точки между двумя узлами колеблются с различными амплитудами, но с одинаковыми фазами (синфазно), так как аргумент синуса в уравнении стоячей волны не зависит от координаты x. При переходе через узел фаза колебаний изменяется скачком на π,так как при этом cos(k*x+α/2) изменяет свой знак на противоположный.

Видео:Урок 375. Стоячие волныСкачать

Стоячие волны. 6.1 Стоячие волны в упругой среде

6.1 Стоячие волны в упругой среде

Согласно принципу суперпозиции, при распростране-нии в упругой среде одновременно нескольких волн воз-никает их наложение, причем волны не возмущают друг друга: колебания частиц среды являются векторной сум-мой колебаний, которые совершали бы частицы при рас-пространении каждой из волн в отдельности.

Волны, создающие колебания среды, разности фаз меж-ду которыми в каждой точке пространства постоянны, на-зываются когерентными.

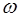
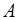
При сложении когерентных волн возникает явление интерференции, заключающееся в том, что в одних точ-ках пространства волны усиливают друг друга, а в других точках – ослабляют. Важный случай интерференции наб-людается при наложении двух встречных плоских волн с одинаковой частотой и амплитудой . Возникающие при этом колебания называют стоячей волной. Чаще все-го стоячие волны возникают при отражении бегущей вол-ны от преграды. При этом падающая волна и отраженная навстречу ей волна при сложении дают стоячую волну.

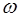
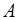
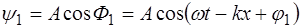
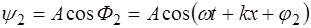
Получим уравнение стоячей волны. Возьмем две плос-кие гармонические волны, распространяющиеся навстечу друг другу вдоль оси X и имеющие одинаковую частоту и амплитуду :

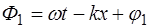
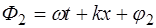
где – фаза колебаний точек среды при про-хождении первой волны;

– фаза колебаний точек среды при про-хождении второй волны.

Разность фаз в каждой точке на оси X не будет зави-сеть от времени, т.е. будет постоянной:

(6.2)

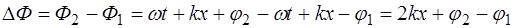
Следовательно, обе волны будут когерентными.

Возникшее в результате сложения рассматриваемых волн колебание частиц среды будет следующим:

. (6.3)

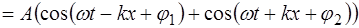
Преобразуем сумму косинусов углов по правилу (4.4) и получим:

(6.4)

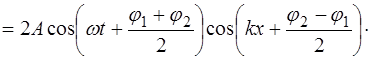
Перегруппировав множители, получим:

(6.5)

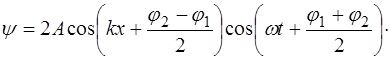
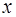
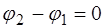
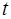
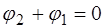
Для упрощения выражения выберем начало отсчета так, чтобы разность фаз и начало отсчета времени , чтобы и сумма фаз была равна нулю: .

Тогда уравнение для суммы волн примет вид:

. (6.6)

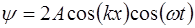
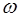
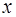
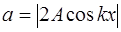
Уравнение (6.6) называется уравнением стоячей вол-ны. Из него видно, что частота стоячей волны равна частоте бегущей волны, а амплитуда, в отличие от бегу-щей волны, зависит от расстояния от начала отсчета :

. (6.7)

С учетом (6.7) уравнение стоячей волны принимает вид:

. (6.8)

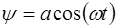
Таким образом, точки среды колеблются с частотой 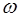, совпадающей с частотой бегущей волны, и амплитудой a, зависящей от положения точки на оси X. Соответственно, амплитуда изменяется по закону косинуса и имеет свои максимумы и минимумы (рис. 6.1).

Уравнение стоячей волны координаты узлов и пучностей

Для того, чтобы наглядно представить расположение минимумов и максимумов амплитуды заменим, согласно (5.29), волновое число его значением:

. (6.9)

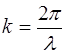
Тогда выражение (6.7) для амплитуды примет вид

(6.10)

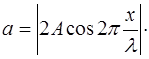
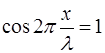
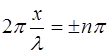
Отсюда становится видно, что амплитуда смещения мак-симальна при , т.е. в точках, координата кото-рых удовлетворяет условию:

, (6.11)

где

Отсюда получаем координаты точек, где амплитуда сме-щения максимальна:

; (6.12)

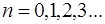
Точки, где амплитуда колебаний среды максимальна, называются пучностями волны.

Амплитуда волны равна нулю в точках, где 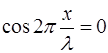. Координата таких точек, называемых узлами волны, удов-летворяет условию:

, (6.13)

где

Из (6.13) видно, что координаты узлов имеют зна-чения:

, (6.14)

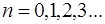
На рис. 6.2 показан примерный вид стоячей волны, от-мечено расположение узлов и пучностей. Видно, что со-седние узлы и пучности смещения отстоят друг от друга на одно и то же расстояние.

Найдем расстояние между соседними пучностями и уз-лами. Из (6.12) получаем расстояние между пучностями:

(6.15)

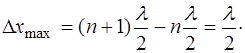
Расстояние между узлами получаем из (6.14):

(6.16)

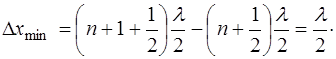
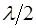
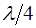
Из полученных соотношений (6.15) и (6.16) видно, что расстояние между соседними узлами, как и между сосед-ними пучностями, постоянно и равно ; узлы и пуч-ности сдвинуты относительно друг друга на (рис. 6.3).

Из определения длины волны можно записать выра-жение для длины стоячей волны: она равна половине дли-ны бегущей волны:

(6.17)

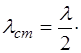
Запишем, с учетом (6.17), выражения для координат уз-лов и пучностей:

, (6.18)

, (6.19)

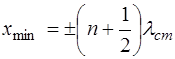
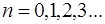
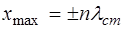
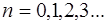
Множитель 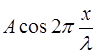, определяющий амплитуду стоя-чей волны, меняет свой знак при переходе через нулевое значение, вследствие чего фаза колебаний по разные сто-роны от узла отличается на . Следовательно, все точки, лежащие по разные стороны от узла, колеблются в про-тивофазе. Все точки, находящиеся между соседними уз-лами, колеблются синфазно.

Узлы условно разделяют среду на автономные области, в которых гармонические колебания совершаются незави-симо. Никакой передачи движения между областями нет, и, значит, перетекания энергии между областями нет. То есть нет передачи возмущения вдоль оси 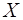. Поэтому волна называется стоячей.

Итак, стоячая волна образуется из двух противополож-но направленных бегущих волн равных частот и амп-литуд. Векторы Умова каждой из этих волн равны по мо-дулю и противоположны при направлению, и при сложе-нии дают ноль. Следовательно, стоячая волна энергии не переносит.

6.2 Примеры стоячих волн

6.2.1 Стоячая волна в струне

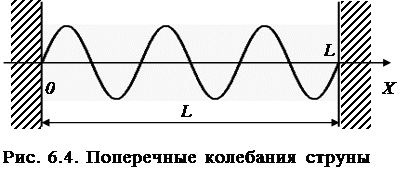
Расмотрим струну длиной L, закрепленную с обоих кон-цов (рис. 6.4).

Расположим вдоль струны ось X таким образом, чтобы левый конец струны имел координату x=0, а правый – x=L. В струне возникают колебания, описываемые урав-нением:

(6.20)

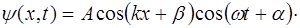
Запишем граничные условия для рассматриваемой стру-ны. Поскольку её концы закреплены, то в точках с коор-динатами x=0 и x=L колебаний нет:

(6.21)

(6.22)

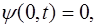
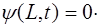
Найдем уравнение колебаний струны исходя из запи-санных граничных условий. Запишем уравнение (6.20) для левого конца струны с учетом (6.21):

(6.23)

Соотношение (6.23) выполняется для любого времени t в двух случаях:

1. . Это возможно в том случае, если коле-бания в струне отсутствуют ( ). Данный случай инте-реса не представляет, и мы его рассматривать не будем.

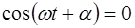
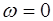
2. . Здесь фаза . Этот случай и позволит нам получить уравнение колебаний струны.

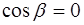
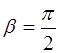
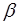
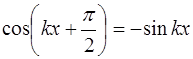
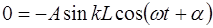
Подставим полученное значение фазы в граничное условие (6.22) для правого конца струны:

. (6.25)

, (6.26)

. (6.27)

Снова возникают два случая, при которых выполняется соотношение (6.27). Случай, когда колебания в струне от-сутствуют ( 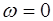), мы рассматривать не будем.

Во втором случае должно выполняться равенство:

, (6.27)

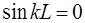
а это возможно, только когда аргумент синуса кратен це-лому числу :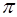

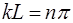
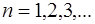
, (6.28)

Значение мы отбрасываем, т.к. при этом , а это означало бы или нулевую длину струны (L=0) или вол-новое число k=0. Учитывая связь (6.9) между волновым числом и длиной волны видно, что для того, чтобы вол-новое число равнялось бы нулю, длина волны должна бы быть бесконечной, а это означало бы отсутствие колебаний.

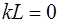
Из (6.28) видно, что волновое число при колебаниях струны, закрепленной с обоих концов, может принимать только определенные дискретные значения:

(6.30)

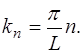
Учитывая (6.9), запишем (6.30) в виде:

(6.31)

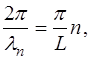
откуда волучаем выражение для возможных длин волн в струне:

(6.31)

Другими словами, на длине струны L должно уклады-ваться целое число n полуволн:

(6.32)

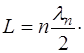
Соответствующие частоты колебаний можно опреде-лить из (5.7):

. (6.33)

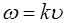
Здесь – фазовая скорость волны, зависящая, соглас-но (5.102), от линейной плотности струны и силы на-тяжения струны :

(6.34)

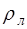
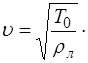
Подставив (6.34) в (6.33), получим выражение, описы-вающее возможные частоты колебаний струны:

, (6.36)

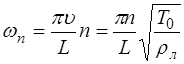
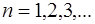
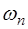
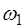
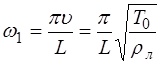
Частоты называют собственными частотами стру-ны. Частоту (при n = 1):

(6.37)

называют основной частотой (или основным тоном) струны. Частоты, определяемые при n>1 называются обертонами или гармониками. Номер гармоники равен n-1. Например, частота :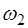

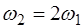
(6.38)

соответствует первой гармонике, а частота :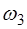

(6.39)

сответствует второй гармонике, и т.д. Поскольку струну можно представить в виде дискретной системы с беско-нечным числом степеней свободы, то каждая гармоника является модой колебаний струны. В общем случае коле-бания струны представляют собой суперпозицию мод.

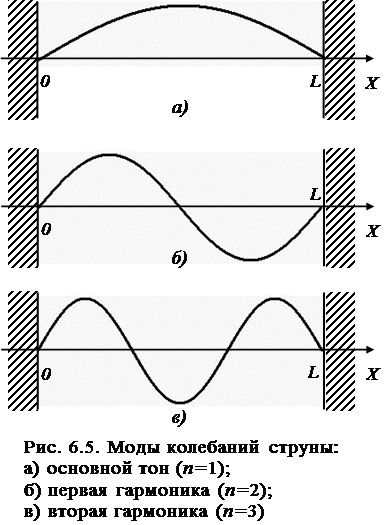Каждой гармонике соответствует своя длина волны. Для основного тона (при n=1) длина волны:

, (6.40)

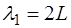
соответственно для первой и второй гармоники (при n=2 и n=3) длины волн будут:

, (6.41)

(6.42)

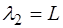
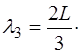
На рис.6.5 показан вид нескольких мод колебаний, осуществляемых струной.

Таким образом, струна с закрепленными концами реа-лизует в рамках классической физики исключительный случай – дискретный спектр частоты колебаний (или длин волн). Таким же образом ведет себя упругий стер-жень с одним или обоими зажатыми концами и колебания воздушного столба в трубах, что и будет рассмотрено в последующих разделах.

6.2.2 Влияние начальных условий на движение

непрерывной струны. Фурье-анализ

Колебания струны с зажатыми концами помимо дис-кретного спектра частот колебаний обладают еще одним важным свойством: конкретная форма колебаний струны зависит от способа возбуждения колебаний, т.е. от на-чальных условий. Рассмотрим подробней.

Уравнение (6.20), описывающее одну моду стоячей вол-ны в струне, является частным решением дифференциаль-ного волнового уравнения (5.61). Поскольку колебание стру-ны складывается из всех возможных мод (для струны – бес-конечное количество), то и общее решение волнового уравнения (5.61) складывается из бесконечного числа частных решений:

, (6.43)

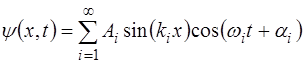
где i – номер моды колебаний. Выражение (6.43) записа-но с учетом того, что концы струны закреплены:

, (6.44)

, (6.45)

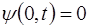
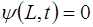
а также с учетом связи частоты i-й моды и ее волнового числа:

(6.46)

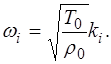
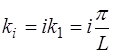
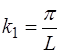
Здесь – волновое число i-й моды;

– волновое число 1-й моды;

Найдем величину начальной фазы для каждой моды колебаний. Для этого в момент времени t=0 придадим струне форму, описываемую функцией f₀(x), выражение для которой получим из (6.43):

. (6.47)

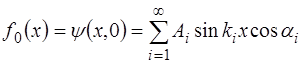
На рис. 6.6 показан пример формы струны, описывае-мой функцией f₀(x).

В момент времени t=0 струна еще покоится, т.е. ско-рость всех ее точек равна нулю. Из (6.43) найдем выраже-ние для скорости точек струны:

, (6.48)

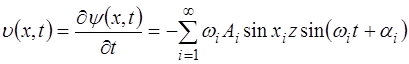
и, подставив в него t=0, получим выражение для скорос-ти точек струны в начальный момент времени:

. (6.49)

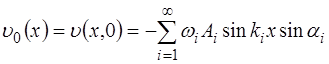
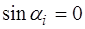
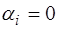
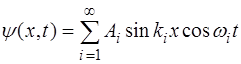
Поскольку в начальный момент времени скорость рав-на нулю, то выражение (6.49) будет равно нулю для всех точек струны, если . Из этого следует, что на-чальная фаза для всех мод тоже равна нулю ( ). С учетом этого выражение (6.43), описывающее движение струны, принимает вид:

, (6.50)

а выражение (6.47), описывающее начальную форму стру-ны, выглядит как:

. (6.51)

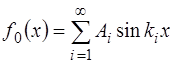
Стоячая волна в струне описывается функцией, перио-дичной на интервале 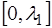, где равна двум длинам струны (рис. 6.7):

. (6.52)

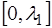
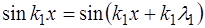
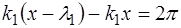
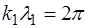
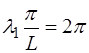
Это видно из того, что периодичность на интервале означает:

. (6.53)

; (6.54)

; (6.55)

, (6.56)

что и приводит нас к выражению (6.52).

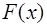
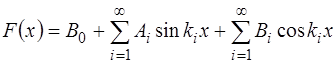
Из математического анализа известно, что любая пе-риодическая функция может быть разложена с высо-кой точностью в ряд Фурье:

, (6.57)

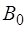
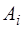
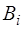
где , , – коэффициенты Фурье.

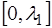
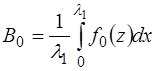
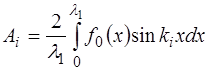
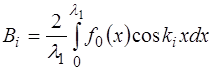
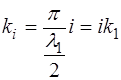
В нашем случае, когда функция является периодичес-кой на интервале , коэффициенты Фурье, согласно [1], рассчитываются как:

, (6.58)

, (6.59)

, (6.60)

. (6.61)

В математике в курсе Фурье-анализа показано, что по-лученные таким образом коэффициенты Фурье для разло-жения периодической функции 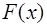фактически и явля-ются коэффициентами разложения функции f₀(x).

Фурье-анализ позволяет разложить колебание, совер-шаемое струной в спектр, т.е. выяснить, какие моды ко-лебаний действительно имеют место при данном способе возбуждения струны.

Рассмотрим два способа возбуждения колебаний струны.

Способ 1. Струне в начальный момент времени прида-ется форма, соответствующая первой моде колебаний и описываемая функцией:

. (6.62)

После того, как струна отпускается, она начинает со-вершать колебания из начального положения. Расчеты по-казывают, что коэффициенты Фурье для этого случая все равны нулю, кроме одного, который равен амплитуде A:

. (6.63)

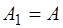
При таком способе возбуждения возникает только одна мода колебаний; никаких обертонов нет.

Способ 2. Струна отводится от положения равновесия посередине, как это происходит в струнных инстру-ментах. Вид начальной формы представлен на рис. 6.8.

Форма струны, изображенная на рис. 6.8, описывается функцией:

при ,

при .

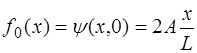
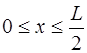
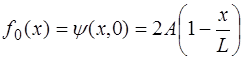
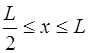
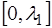
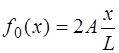
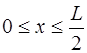
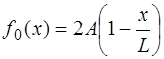
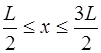
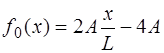
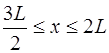
Функция, соответствующая (6.64), и которая является пе-риодической на интервале , записывается следую-щим образом:

при ,

при , (6.65)

при .

Вид периодической функции (6.65) показан на рис.6.9:

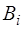
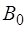
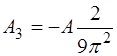
Расчеты показывают, что все коэффициенты Фурье для такой функции равны нулю (включая и коэффициент ). Первые три коэффициента A₁, A₂, A₃ соответственно равны:

, (6.66)

, (6.67)

. (6.68)

Как уже отмечалось, полученные таким образом коэф-фициенты Фурье для разложения периодической функ-ции фактически и являются коэффициентами разло-жения функции f₀(x).

Тогда, с учетом трех первых слагаемых ряда Фурье, функция (6.64) может быть приближенно представлена следующим образом:

(6.69)

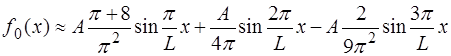
Мы нашли только три первых члена Фурье-разложения функции (6.64). Конечно, полученный нами ряд Фурье (6.69) при конечном количестве членов, в нашем случае равном трём, может воспроизвести исходную функцию лишь при-ближённо. Однако, вычисления коэффициентов Фурье могут быть продолжены. Получится, что при рассматриваемом на-ми случае колебаний в струне возникает много гармоник (теоретически, бесконечный ряд гармоник).

Сравнивая первый и второй рассмотренные случаи, мы видим, что в первом из них была только одна мода, а во втором возникает много гармоник.

Таким образом, рассмотренные случаи показывают, что конкретная форма колебаний струны, зажатой с двух сторон, существенно зависит от способа возбуждения ко-лебаний, т.е., от начальных условий.