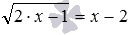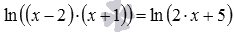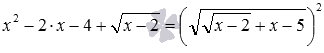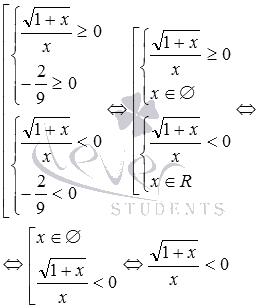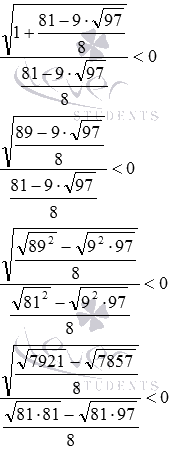Решение уравнений через переход к уравнениям-следствиям может привести к появлению так называемых посторонних корней. В этой статье мы, во-первых, детально разберем, что такое посторонние корни. Во-вторых, поговорим о причинах их возникновения. И в-третьих, на примерах рассмотрим основные способы отсеивания посторонних корней, то есть, проверки корней на предмет наличия среди них посторонних с целью исключения их из ответа.
- Посторонние корни уравнения, определение, примеры
- Причины возможного появления посторонних корней
- Что такое отсеивание посторонних корней?
- Способы отсеивания посторонних корней
- Проверка подстановкой
- По ОДЗ
- По условиям ОДЗ
- Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
- Уравнения-следствия: возведение уравнения в четную степень. 11-й класс
- Ход уроков
- I. Актуализация знаний
- II. Разбор теории: Возведение уравнения в чётную степень
- Возведение уравнения в четную степень не может привести к появлению посторонних корней
- 💥 Видео
Видео:11 класс, 26 урок, Равносильность уравненийСкачать

Посторонние корни уравнения, определение, примеры
В школьных учебниках по алгебре не дается определение постороннего корня. Там представление о постороннем корне формируется путем описания следующей ситуации: при помощи некоторых преобразований уравнения осуществляется переход от исходного уравнения к уравнению-следствию, находятся корни полученного уравнения-следствия, и осуществляется проверка найденных корней подстановкой в исходное уравнение, которая показывает, что некоторые из найденных корней не являются корнями исходного уравнения, эти корни называют посторонними корнями для исходного уравнения [1, с. 174-175; 2, с. 202; 3, с. 187-188].
Отталкиваясь от этой базы, для себя можно принять такое определение постороннего корня:
Посторонние корни – это корни полученного в результате проведения преобразований уравнения-следствия, не являющиеся корнями исходного уравнения.
Приведем пример. Рассмотрим уравнение 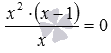
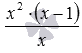
Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать

Причины возможного появления посторонних корней
Если для получения уравнения-следствия не использовать никакие «экзотические» преобразования, а использовать только основные преобразования уравнений, то посторонние корни могут возникнуть лишь по двум причинам:
- из-за расширения ОДЗ и
- из-за возведения обеих частей уравнения в одну и ту же четную степень.
Здесь стоит напомнить, что расширение ОДЗ в результате преобразования уравнения в основном происходит
- При сокращении дробей;
- При замене нулем произведения с одним или несколькими нулевыми множителями;
- При замене нулем дроби с нулевым числителем;
- При использовании некоторых свойств степеней, корней, логарифмов;
- При использовании некоторых тригонометрических формул;
- При умножении обеих частей уравнения на одно и то же выражение, обращающееся в нуль на ОДЗ для этого уравнения;
- При освобождении в процессе решения от знаков логарифмов.
Пример из предыдущего пункта статьи иллюстрирует появление постороннего корня из-за расширения ОДЗ, которое имеет место при переходе от уравнения 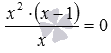
Также приведем пример появления постороннего корня из-за возведения обеих частей уравнения в одну и ту же четную степень. Иррациональное уравнение 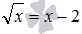
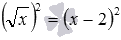
Заметим, что расширение ОДЗ и возведение обеих частей уравнения в одну и ту же четную степень, не всегда приводит к появлению посторонних корней. Например, при переходе от уравнения 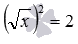
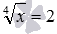
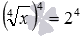
Видео:СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать

Что такое отсеивание посторонних корней?
Термин «отсеивание посторонних корней» лишь с натяжкой можно назвать устоявшимся, он встречается далеко не во всех учебниках алгебры, но является интуитивно понятным, из-за чего обычно и используется. Что понимают под отсеиванием посторонних корней, становится понятно из следующей фразы: «… проверка – обязательный этап решения уравнения, который поможет обнаружить посторонние корни, если они есть, и отбросить их (обычно говорят «отсеять»)» [1, с.176].
Отсеивание посторонних корней – это обнаружение и отбрасывание посторонних корней.
Теперь можно переходить к способам отсеивания посторонних корней.
Видео:8 класс, 38 урок, Иррациональные уравненияСкачать

Способы отсеивания посторонних корней
Проверка подстановкой
Основной способ отсеивания посторонних корней – это проверка подстановкой. Он позволяет отсеять посторонние корни, которые могли возникнуть и по причине расширения ОДЗ, и по причине возведения обеих частей уравнения в одну и ту же четную степень.
Проверка подстановкой состоит в следующем: найденные корни уравнения-следствия по очереди подставляются в исходное уравнение или в любое равносильное ему уравнение, те из них, которые дают верное числовое равенство, являются корнями исходного уравнения, а те, которые дают неверное числовое равенство или выражение, не имеющее смысла, являются посторонними корнями для исходного уравнения.
Покажем на примере, как проводится отсеивание посторонних корней через подстановку в исходное уравнение.
Решите уравнение
В некоторых случаях отсеивание посторонних корней целесообразнее проводить другими способами. Это относится в основном к тем случаям, когда проверка подстановкой связана со значительными вычислительными трудностями или когда стандартный способ решения уравнений какого-то определенного вида предполагает другой проверки (например, отсеивание посторонних корней при решении дробно-рациональных уравнений проводится по условию не равенства нулю знаменателя дроби). Разберем альтернативные способы отсеивания посторонних корней.
По ОДЗ
В отличие от проверки подстановкой, отсеивание посторонних корней по ОДЗ уместно не всегда. Дело в том, что этот способ позволяет отсеивать лишь посторонние корни, возникающие по причине расширения ОДЗ, и он не гарантирует отсеивание посторонних корней, которые могли возникнуть по другим причинам, например, из-за возведения обеих частей уравнения в одну и ту же четную степень. Более того, не всегда просто отыскать ОДЗ для решаемого уравнения. Тем не менее, способ отсеивания посторонних корней по ОДЗ стоит держать на вооружении, так как часто его использование требует меньших вычислительных работ, чем использование других способов.
Отсеивание посторонних корней по ОДЗ проводится следующим образом: все найденные корни уравнения-следствия проверяются на предмет принадлежности области допустимых значений переменной для исходного уравнения или любого равносильного ему уравнения, те из них, которые принадлежат ОДЗ, являются корнями исходного уравнения, а те из них, которые не принадлежат ОДЗ, являются посторонними корнями для исходного уравнения.
Анализ приведенной информации приводит к выводу, что отсеивание посторонних корней по ОДЗ целесообразно проводить, если единовременно:
- легко находится ОДЗ для исходного уравнения,
- посторонние корни могли возникнуть только по причине расширения ОДЗ,
- проверка подстановкой связана со значительными вычислительными сложностями.
Покажем, как проводится отсеивание посторонних корней, на практике.
Решите логарифмическое уравнение
По условиям ОДЗ
Как мы сказали в предыдущем пункте, если посторонние корни могли возникнуть лишь по причине расширения ОДЗ, то их можно отсеять по ОДЗ для исходного уравнения. Но не всегда просто найти ОДЗ в виде числового множества. В таких случаях можно проводить отсеивание посторонних корней не по ОДЗ, а по условиям, определяющим ОДЗ. Разъясним, как проводится отсеивание посторонних корней по условиям ОДЗ.
Найденные корни по очереди подставляются в условия, определяющие ОДЗ для исходного уравнения или любого равносильного ему уравнения. Те из них, которые удовлетворяют всем условиям, являются корнями уравнения. А те из них, которые не удовлетворяют хотя бы одному условию или дают не имеющее смысла выражение, являются посторонними корнями для исходного уравнения.
Приведем пример отсеивания посторонних корней по условиям ОДЗ.
Решить иррациональное уравнение
Отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в четную степень
Понятно, что отсеивание посторонних корней, возникающих из-за возведения обеих частей уравнения в одну и ту же четную степень, можно осуществить путем подстановки в исходное уравнение или в любое равносильное ему уравнение. Но такая проверка может быть связана со значительными вычислительными трудностями. На этот случай стоит знать альтернативный способ отсеивания посторонних корней, о котором мы сейчас и поговорим.
Отсеивание посторонних корней, которые могут возникнуть при возведении в одну и ту же четную степень обеих частей иррациональных уравнений вида 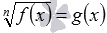
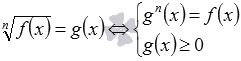
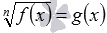
Покажем, как на практике отсеиваются посторонние корни указанным способом.
Решите уравнение
В заключение скажем, что рассмотренный подход является частным случаем более общего подхода к отсеиванию посторонних корней, возникающих при возведении обеих частей уравнения в одну и ту же четную степень. Отсеять посторонние корни, которые могут возникнуть при возведении обеих частей уравнения f(x)=g(x) в одну и ту же четную степень, можно по условию 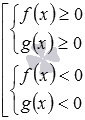
Приведем пример отсеивания посторонних корней предложенным способом. Возьмем уравнение 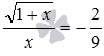
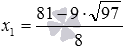

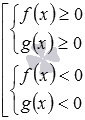
Подстановка в неравенство 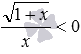
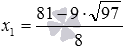
Полученное неравенство верное, так как в числителе положительное число, а в знаменателе – отрицательное, поэтому, отношение этих чисел есть отрицательное число. Значит, 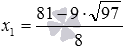
Подстановка в неравенство 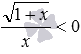

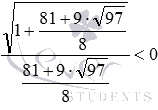

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Уравнения-следствия: возведение уравнения в четную степень. 11-й класс
Разделы: Математика
Класс: 11
Продолжительность: 2 урока.
Цель урока:
- (для учителя) формирование у учащихся целостного представления о методах решения иррациональных уравнений.
- (для учащихся) Развитие умения наблюдать, сравнивать, обобщать, анализировать математические ситуации (слайд 2). Подготовка к ЕГЭ.
План первого урока (слайд 3)
- Актуализация знаний
- Разбор теории: Возведение уравнения в чётную степень
- Практикум по решению уравнений
План второго урока
- Дифференцированная самостоятельная работа по группам «Иррациональные уравнения на ЕГЭ»
- Итог уроков
- Домашнее задание
Видео:Решение биквадратных уравнений. 8 класс.Скачать

Ход уроков
I. Актуализация знаний
Цель: повторить понятия, необходимые для успешного освоения темы урока.
– Какие два уравнения называются равносильными?
– Какие преобразования уравнения называют равносильными?
– Данное уравнение заменить равносильным с пояснением применённого преобразования: (слайд 4)
а) х



– Какое уравнение называют уравнением-следствием исходного уравнения?
– Может ли уравнение-следствие иметь корень, не являющийся корнем исходного уравнения? Как называются эти корни?
– Какие преобразования уравнения приводят к уравнениям-следствиям?
– Что называется арифметическим квадратным корнем?
Остановимся сегодня более подробно на преобразовании «Возведение уравнения в чётную степень».
II. Разбор теории: Возведение уравнения в чётную степень
Объяснение учителя при активном участии учащихся:
Пусть 2m (m


Очень часто это утверждение применяется при решении иррациональных уравнений.
Определение. Уравнение, содержащее неизвестное под знаком корня, называется иррациональным.
При решении иррациональных уравнений используют следующие методы: (слайд 5)
Переход к равносильной системе:
а) 



Из двух систем решают ту, которая проще.
б) 

если а ≥ 0, то 


если а 19.06.2011
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Возведение уравнения в четную степень не может привести к появлению посторонних корней
_____________ системы трех уравнений с тремя неизвестными называют такую упорядоченную тройку чисел (х0; у0; z0), при подстановке которой в каждое из уравнений системы имеют смысл выражения f1(х0; y0; z0), g1(х0; у0; z0), f2(x0; y0; z0), g2(x0; y0; z0), f3(х0; у0; z0), g3(x0; y0; z0) и справедливы числовые равенства:
Верны ли утверждения?
А) Возведение неравенства в нечетную степень 2m + 1 (mÎN) приводит данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел
В) Логарифмирование неравенства a f(x)>a g(x) т.е. заменa этого неравенства при а>1 неравенством f(x)>g(x), а при 0 1 неравенством f(x)>g(x), а при 0 0 не имеет решений
В) Множество всех решений неравенства |х2 – 4| +|x + 1| – 3 > 0 на промежутке [-1; 2) составляет интервал (-1; 2)
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке (-∞; -2] по определению абсолютной величины |х2-4| = х2-4
В) На промежутке (-∞; -2] по определению абсолютной величины |x + 1| = -x- 1
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке (-∞; 1) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению: -(x — 1) — (x — 2) — (x — 3) = 6
В) На промежутке (-∞; 1) уравнение |x — 1| + |x — 2| + |x — 3| = 6 имеет один корень
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [-1; 2): |х2-4| = -х2 + 4
В) На промежутке [-1; 2): |x+1| = -x-1
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [1; 2) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению: x — 1 + x – 2 + x — 3 = 6
В) На промежутке [1; 2) уравнение |x — 1| + |x — 2| + |x — 3| = 6 имеет единственный корень, равный 1,5
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [1; 2) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению: x — 1 -(x-2)-(x-3) = 6
В) На промежутке [1; 2) уравнение |x — 1| + |x — 2| + |x — 3| = 6 не имеет корней
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [2; +∞) |х2-4| = -х2 + 4
В) На промежутке [2; +∞) |x+1| = -x-1
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [2; +∞) |х2-4| = х2 — 4
В) На промежутке [2; +∞) |x+1| = x+1
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [2; 3) уравнение |x — 1| + |x — 2| + |x — 3| = 6 не имеет корней
В) На промежутке [2; 3) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению x-1 + x-2-(x-3) = 6
Подберите правильный ответ
Верны ли утверждения?
А) На промежутке [3; +∞) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению x-1+x-2+x-3 = 6
В) На промежутке [3; +∞) уравнение |x-1| + |x-2| + |x-3| = 6 имеет единственный корень 4
Подберите правильный ответ
Верны ли утверждения?
А) Неравенства >1 и х2 > 1 не являются равносильными на множестве всех действительных чисел, но они равносильны на множестве всех положительных чисел
В) Неравенства x>1 и x3>1 являются равносильными на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Неравенства af(x)>ag(x) и f(x)>g(x) равносильны при 0 ag(x) и f(x) ag(x) и f(x)>g(x) равносильны при a > 1
В) Неравенства af(x)>ag(x) и f(x) 1
Подберите правильный ответ
Верны ли утверждения?
А) Неравенства af(x)>ag(x) и f(x)>g(x) равносильны при а > 1
В) Неравенства af(x)>ag(x) и f(x) logag(x) при а>1 равносильно двойному неравенству: 0 logag(x) при 0 g(x)>0
Подберите правильный ответ
Верны ли утверждения?
А) Неравенство logaf(x)>logag(x) при а>1 равносильно двойному неравенству: f(x)>g(x)>0
В) Неравенство logaf(x)>logag(x) при 0 0, а≠1) приводит к уравнению f(x) = g(x), равносильному исходному на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Перенос члена неравенства (с противоположным знаком) из одной части неравенства в другую приводит данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел
В) Умножение (деление) обеих частей неравенства на положительное число приводит данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Перенос члена уравнения (с противоположным знаком) из одной части уравнения в другую приводит данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
В) Умножение (деление) обеих частей уравнения на не равное нулю число приводит данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Переход от уравнения log2(х5 + х2 – 4) = log2(х5 + 4х – 7) к уравнению-следствию х5 + х2 — 4 = х5 + 4х – 7 осуществляется при помощи потенцирования исходного уравнения
В) Уравнение 2х — 14 = х2 — 6х – 7 является следствием уравнения
Подберите правильный ответ
Верны ли утверждения?
А) Потенцирование уравнения lg(x2-4) = lg(4x-7) приводит к уравнению-следствию: х2 — 4 = 4х — 7, имеющему корень, посторонний для исходного уравнения
В) Освобождение уравнения от знаменателей приводит к уравнению-следствию (х2-1)(x + 3) = (х2-9)(x-2), имеющему корень, посторонний для исходного уравнения
Подберите правильный ответ
Верны ли утверждения?
А) При переходе к уравнению-следствию невозможно потерять корни исходного уравнения
В) Если при решении данного уравнения совершен переход к уравнению-следствию, то необходимо проверить, все ли корни уравнения-следствия являются корнями исходного уравнения
Подберите правильный ответ
Верны ли утверждения?
А) При решении уравнений нельзя применять преобразования, приводящие к потере корней исходного уравнения
В) Уравнение: , являющееся следствием уравнения имеет корень, посторонний для уравнения
Подберите правильный ответ
Верны ли утверждения?
А) Приведение подобных членов (f(x) — f(x)=0) приводит к уравнению, равносильному исходному на том множестве М, на котором определена функция f(x)
В) Применение некоторых формул (логарифмических, тригонометрических и др.) приводит к уравнению, равносильному исходному на том множестве М, на котором одновременно определены обе части применяемой формулы
Подберите правильный ответ
Верны ли утверждения?
А) Приведение подобных членов уравнения приводит к уравнению-следствию
В) Если при решении некоторого уравнения проводилось приведение подобных членов, то необходима проверка всех найденных корней
Подберите правильный ответ
Верны ли утверждения?
А) Применение правил умножения многочленов и формул сокращенного умножения многочленов приводит данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел
В) Приведение подобных членов многочлена, не зависящих от х, приводит данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Применение правил умножения многочленов и формул сокращенного умножения многочленов приводит данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
В) Приведение подобных членов многочлена, не зависящих от x, приводит данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Простейшее логарифмическое уравнение — уравнение: loga х = b, где а — данное положительное, не равное 1 число, b — данное действительное число
В) Простейшее показательное уравнение — уравнение: ах = b, где а — данное положительное, не равное 1 число, b — данное действительное число
Подберите правильный ответ
Верны ли утверждения?
А) Простейшие логарифмические неравенства — неравенства: loga x > b и loga x b, ах g(x) и
В) Пусть 2m + 1 — нечетное натуральное число (m Î N), тогда равносильны неравенства:
Подберите правильный ответ
Верны ли утверждения?
А) Пусть 2m — четное натуральное число (m Î N) и пусть на некотором множестве М обе функции f(x) и g(x) неотрицательны, тогда на этом множестве равносильны уравнения: f(x) = g(x) и
В) Пусть 2m+ 1 — нечетное натуральное число (m Î N), тогда равносильны уравнения: f(x) = g(x) и
Подберите правильный ответ
Верны ли утверждения?
А) Пусть n — фиксированное четное натуральное число. Тогда уравнение: (f(x))n = (g(x))n является следствием уравнения f(x) = g(x)
В) Уравнения, содержащие неизвестное под знаком корня — иррациональные уравнения
Подберите правильный ответ
Верны ли утверждения?
А) Пусть n — фиксированное четное натуральное число. Тогда уравнение: f(x) = g(x) является следствием уравнения (f(x))n = (g(x))n
В) Пусть а — данное число, такое, что а>0 и а≠1. Тогда уравнение: f(x) = g(x) является следствием уравнения logaf(x) = logag(x)
Подберите правильный ответ
Верны ли утверждения?
А) Пусть R — область существования функции f(u) и пусть эта функция непрерывна на R. Тогда если функция f(u) возрастает на R, то равносильны неравенства f(a(x))>f(b(x)) и a(x)>b(x)
В) Пусть R — область существования функции f(u) и пусть эта функция непрерывна на R. Тогда если функция f(u) убывает на R, то равносильны неравенства f(a(x))>f(b(x)) и a(x) c и f(x)>ac при 0 ac при 0 c и f(x)>ac при 0 ac при а>1
Подберите правильный ответ
Верны ли утверждения?
А) Пусть а и с — данные числа, тогда равносильны неравенства: logaf(x)>c и f(x)>ac при а>1
В) Пусть а и с — данные числа, тогда равносильны неравенства: loga f(x) ac при 0 c и f(x)>ac при а>1
В) Пусть а и с — данные числа, тогда равносильны неравенства: loga f(x) ac при а>1
Подберите правильный ответ
Верны ли утверждения?
А) Пусть на некотором множестве М обе функции f(x) и g(x) положительны, тогда на множестве М равносильны неравенства: logaf(x) > logag(x) и f(x) > g(x) при а>1
В) Пусть на некотором множестве М обе функции f(x) и g(x) положительны, тогда на множестве М равносильны неравенства: logaf(x) > logag(x) и f(x) logag(x) и f(x) > g(x) при а>1
В) Пусть на некотором множестве М обе функции f(x) и g(x) положительны, тогда на множестве М равносильны неравенства: logaf(x) > logag(x) и f(x) > g(x) при 0 logag(x) и f(x) 1
В) Пусть на некотором множестве М обе функции f(x) и g(x) положительны, тогда на множестве М равносильны неравенства: logaf(x) > logag(x) и f(x) g(x) и f(x)j(x)>g(x)j(x)
В) Пусть на некотором множестве М функция j(x) отрицательна, тогда на этом множестве равносильны неравенства f(x)>g(x) и f(x)j(x) f(b(x)) равносильно системе:
В) Пусть область существования функции f(u) есть промежуток М и пусть эта функция непрерывна на промежутке М. Тогда если функция f(u) убывает на этом промежутке М, то неравенство f(a(x))>f(b(x)) равносильно системе:
Подберите правильный ответ
Верны ли утверждения?
А) Пусть фиксированное число а таково, что а>0 и а ≠ 1, и пусть на некотором множестве М обе функции f(x) и g(x) положительны. Тогда на множестве М уравнения: f(x) = g(x) и равносильны
В) Пусть фиксированное число а таково, что а g(x) неравенством: f(x)j(x)>g(x)j(x), является равносильным преобразованием только на том множестве М, на котором функция j(x) положительна
В) Приведение подобных членов (f(x) — f(x) = 0) приводит к неравенству, равносильному исходному только на том множестве М, на котором определена функция f(x)
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение 2log2x = 1 имеет два корня
В) Уравнение log2x2=1 имеет два корня
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение 2log2x = 1 имеет один корень
В) Уравнение log2x2=1 имеет один корень
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение один корень
В) Уравнение х2 — 4х + 3 = 2х – 5 имеет два корня
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение имеет два корня
В) Уравнение х2 = 1 имеет только один корень
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение имеет только один корень
В) Уравнение х2 = 1 имеет два корня
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение равносильно совокупности нескольких систем, если любое решение уравнения является решением хотя бы одной из этих систем, а любое решение каждой из систем является решением уравнения
В) Неравенство равносильно совокупности нескольких систем, если любое решение неравенства является решением хотя бы одной из этих систем, а любое решение каждой из систем является решением неравенства
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение х2 – x — 6 = 0 имеет два корня: х1 = 3 и х2 = -2
В) Уравнение х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1) имеет единственный корень х1= 3
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение х2 = 1 есть следствие уравнения
В) Уравнение есть следствие уравнения х2 = 1
Подберите правильный ответ
Верны ли утверждения?
А) Уравнение: х2 – x — 6 = 0 является следствием уравнения х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1)
В) Уравнение х2 – x — 6 = 0 имеет единственный корень х1= 3
Подберите правильный ответ
Верны ли утверждения?
А) Уравнения 2log2x = 1 и log2x2=1 не являются равносильными на множестве всех действительных чисел
В) Уравнения 2log2x = 1 и log2x2=1 являются равносильными на множестве всех положительных действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Уравнения =1 и х2=1 не являются равносильными на множестве всех действительных чисел
В) Уравнения =1 и х2=1 являются равносильными на множестве всех неотрицательных действительных чисел
Подберите правильный ответ
Верны ли утверждения?
А) Уравнения и х2 = 1 не являются равносильными на множестве всех действительных чисел
В) Уравнения и х2 = 1 являются равносильными на множестве всех целых чисел
Подберите правильный ответ
Верны ли утверждения?
А) Число 1 является корнем уравнения
В) Число 1 является корнем уравнения (log2x)2 – 2log2x = 0
Подберите правильный ответ
Верны ли утверждения?
А) Число х1= 3 является корнем уравнения х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1)
В) Число х2= -2 не является корнем уравнения х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1)
Подберите правильный ответ
__________
____________ (а; b) — множество всех действительных чисел x, удовлетворяющих двойному неравенству а 0 надо решить уравнения х2-4=0 и x+1=0 и отметить на координатной оси полученные корни: __________
Для решения нестрогого неравенства f(x) ³ g(x) надо: решить ____________
Если два неравенства равносильны на множестве всех действительных чисел, то говорят, что неравенства ______________
Если два уравнения равносильны на множестве всех действительных чисел, то в таких случаях говорят, что уравнения _____________
Если к уравнению применить формулу , то получится уравнение: ______________, которое является следствием исходного уравнения
Если множество решений системы уравнений пустое, то в этом случае говорят, что система ____________________ (два варианта)
Если уравнение x2 — 2x + log2x = 3 + log2x имеет корни, то эти корни принадлежат множеству М = _________________
Замену одного неравенства другим неравенством, равносильным ему на множестве М, называют
Замену одного уравнения другим уравнением, равносильным ему на множестве М, называют равносильным ___________ на множестве М от одного уравнения к другому
Замену разности f(x) — f(x) нулем называют ____________________
Иногда для записи равносильности уравнений, неравенств, систем, совокупностей систем употребляют знак ____.
Иногда для записи совокупности систем их записывают друг под другом и объединяют скобкой вида: ___
К системе-следствию приводят следующие преобразования: __________________
Каждое из неравенств f(x)g(x)>0 и равносильно совокупности двух систем _____
Корень уравнения 2log2x = 1 равен х1= ____
Корень уравнения log2(х5 + х2 – 4) = log2(х5 + 4х – 7) равен _________________
Корень уравнения log2x2=1 равны: ____
Корень уравнения равен _________________
Корень уравнения равен: ______________
Корень уравнения: равен _______________
Корни уравнения (log2x)2 – 2log2x = 0 равны: ______________
Корни уравнения 2х — 14 = х2 — 6х – 7 равны: _________________
Любое решение уравнения lg(1 – x2) = lg 2x находится на множестве М = _________
Множество всех решений неравенства: есть интервал _____________
На множестве всех положительных чисел каждое из уравнений: 2log2x = 1 и log2x2=1 имеет только один корень х = _______
На множестве М=(0; 1) уравнение lg(1 – x2) = lg 2x равносильно уравнению
На промежутках ____________ уравнение |x — 1| + |x — 2| + |x — 3| = 6 не имеет корней
На промежутке (-2; -1) неравенство |х2 – 4| +|x + 1| – 3 > 0 равносильно неравенству: ____________________
На промежутке (-∞; -2] неравенство |х2 – 4| +|x + 1| – 3 > 0 равносильно неравенству: ____________________
На промежутке (-∞; 1) по определению абсолютной величины: ____________
На промежутке (-∞; 1) уравнение |x — 1| + |x — 2| + |x — 3| = 6 имеет единственный корень, равный ____
На промежутке (-∞; 1) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению: __________________
На промежутке [-1; 2) неравенство |х2 – 4| +|x + 1| – 3 > 0 равносильно неравенству:
На промежутке [1; 2) по определению абсолютной величины: ____________
На промежутке [1; 2) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению: ________________
На промежутке [2; +∞) неравенство |х2 – 4| +|x + 1| – 3 > 0 равносильно неравенству:
На промежутке [2; 3) по определению абсолютной величины: _____________________
На промежутке [2; 3) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению ____________________
На промежутке [3; +∞) по определению абсолютной величины: ____________
На промежутке [3; +∞) уравнение |x — 1| + |x — 2| + |x — 3| = 6 равносильно уравнению ____________________
Неравенства af(x)>ag(x) и f(x)>g(x) равносильны при _________
Неравенства af(x)>ag(x) и f(x) 0 равносильно совокупности систем: ______________
Неравенство равносильно совокупности систем _____________
Неравенство равносильно системе
Неравенство равносильно системе __________
Неравенство равносильно совокупности двух систем _____
Неравенство равносильно двойному неравенству _____
Неравенство log2(3x — 1) g(x) + j(x) равносильно системе ____________
Неравенство logaf(x)>logag(x) при 0 logag(x) при а > 1 равносильно двойному неравенству ______________
Неравенство |f(x)| |x + 6| имеет множество решений: _____________
Объединение множеств А и В обозначают
Освобождение уравнения от знаменателей приводит к уравнению-следствию (х2-1)(x + 3) = (х2-9)(x-2), имеющему корень _______, посторонний для исходного уравнения
Переход от уравнения log2(х5 + х2 – 4) = log2(х5 + 4х – 7) к уравнению-следствию х5 + х2 — 4 = х5 + 4х – 7 осуществляется при помощи _______________ исходного уравнения
Полуинтервал [а; b) множество всех действительных чисел, удовлетворяющих ___________
Полуинтервал [а; b) множество точек оси x, состоящее из
Потенцирование уравнения lg(x2-4) = lg(4x-7) приводит к уравнению-следствию: х2 — 4 = 4х — 7, имеющему корень, равный _________, посторонний для исходного уравнения
Преобразования неравенства, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел: _______________
Преобразования неравенства, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел: _______________
Преобразования неравенства, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел: _______________.
Преобразования неравенства, приводящие исходное неравенство к неравенству, равносильному ему на некотором множестве чисел, но не равносильному на множестве всех действительных чисел: _______________
Преобразования неравенства, приводящие исходное неравенство к неравенству, равносильному ему на некотором множестве чисел, но не равносильному на множестве всех действительных чисел: _______________
Преобразования уравнения, приводящие данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
Преобразования уравнения, приводящие данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
Преобразования уравнения, приводящие данное уравнение к уравнению, равносильному ему на множестве всех действительных чисел
Преобразования уравнения, приводящие исходное уравнение к уравнению, равносильному ему на некотором множестве чисел, но не равносильному на множестве всех действительных чисел
Преобразования уравнения, приводящие исходное уравнение к уравнению, равносильному ему на некотором множестве чисел, но не равносильному на множестве всех действительных чисел
Преобразования уравнения, приводящие исходное уравнение к уравнению, равносильному ему на некотором множестве чисел, но не равносильному на множестве всех действительных чисел
При решении неравенства: |х2 – 4| +|x + 1| – 3 > 0 после того, как отметили на координатной оси полученные корни, обращающие в ноль выражения под знаком модуля, получаются четыре числовых промежутка: __________
Простейшее логарифмическое уравнение — уравнение __________________
Простейшее показательное уравнение — уравнение __________________
Простейшие логарифмические неравенства — неравенства __________________
Простейшие показательные неравенства — неравенства __________________
Пусть n — фиксированное четное натуральное число. Тогда уравнение: (f(x))n = (g(x))n является следствием уравнения f(x) = g(x)
Пусть R — область существования функции f(u) и пусть эта функция непрерывна на R. Тогда если функция f(u) возрастает на R, то равносильны неравенства ________________
Пусть R — область существования функции f(u) и пусть эта функция непрерывна на R. Тогда если функция f(u) убывает на R, то равносильны неравенства ________________
Пусть а и с — данные числа, тогда равносильны неравенства: loga f(x)>c и f(x)>ac при _____
Пусть а и с — данные числа, тогда равносильны неравенства: loga f(x) ac при _____
Пусть дано несколько уравнений и несколько неравенств с неизвестным x и пусть требуется найти все числа x, каждое из которых удовлетворяет каждому из этих уравнений и неравенств. Тогда говорят, что дана _________ уравнений и неравенств
Пусть даны два уравнения: f(x) = g(x) и р(x) = j(x). Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называют __________ первого
Пусть область существования функции f(u) есть промежуток М и пусть эта функция непрерывна и строго монотонна (т.е. возрастает или убывает) на этом промежутке. Тогда уравнение: f(a(x))= f(b(x)) равносильно системе ______________
Пусть область существования функции f(u) есть промежуток М и пусть эта функция непрерывна на промежутке М. Тогда если функция f(u) убывает на этом промежутке М, то неравенство f(a(x))>f(b(x)) равносильно системе ______________
Пусть область существования функции f(u) есть промежуток М и пусть эта функция непрерывна на промежутке М. Тогда, если функция f(u) возрастает на этом промежутке М, то неравенство f(a(x))>f(b(x)) равносильно системе ______________
Пусть число а таково, что а>0, а≠1. Тогда уравнение: равносильно системе
Расположите по порядку действия необходимые для решения неравенства: |х2 – 4| +|x + 1| – 3 > 0
Расположите числовые промежутки в порядке увеличения количества целых чисел, принадлежащих этим промежуткам
Система, равносильная исходной системе, получается также, если в одном из уравнений: __________________
Система-____________ данной системы уравнений — система уравнений, для которой является решением каждое решение данной системы уравнений
Систему уравнений: называют ____________ системы если каждое решение второй системы является решением первой системы
Следствием уравнения является уравнение: __________________
Следствием уравнения является уравнение: __________________
Следствием уравнения является уравнение: __________________
Следствием уравнения является уравнение: ______________
Уравнение (log2x)2 – 2log2x = 0 имеет ______________ корень(ня)
Уравнение (sinx — 1)(tgx — 1) = 0 равносильно совокупности систем _______________
Уравнение 1 — х2 = 2х имеет __________ корень(ня)
Уравнение 2log2x = 1 имеет ______________ корень(ня)
Уравнение 2х — 14 = х2 — 6х – 7 _________________ корерь(ня, ей)
Уравнение равносильно системе ____________
Уравнение равносильно системе ____________
Уравнение равносильно системе ____________
Уравнение равносильно системе ____________
Уравнение равносильно системе ____________
Уравнение равносильно системе: ___________
Уравнение lg(1 – x2) = lg 2x имеет __________ корень(ня)
Уравнение lg(1 – x2) = lg 2x имеет корень _________
Уравнение log2(х5 + х2 – 4) = log2(х5 + 4х – 7) _________________ корень(ня, ей)
Уравнение log2x2=1 имеет ______________ корня(ня)
Уравнение sin 6x = 0 имеет только _____________________ серию(и) решений
Уравнение sin 6x = 0 имеет только одну серию решений _______________,
Уравнение имеет корни, равные
Уравнение равносильно уравнению
Уравнение ________________ корень(ня, ей)
Уравнение единственный корень х1= ________________
Уравнение равносильно совокупности систем _______________
Уравнение имеет только _____________________ серию(и) решений
Уравнение имеет только одну серию решений _______________,
Уравнение _________________ корень(ня, ей)
Уравнение имеет ______________ корень(ня)
Уравнение имеет ______________ корень(ня)
Уравнение f(x) + j(x) = g(x) + j(x) равносильно системе ____________
Уравнение ___________ является следствием уравнения
Уравнение _____________ является следствием уравнения
Уравнение |f(x)| = g(x) равносильно совокупности систем _______________
Уравнение |x + 1| = 2х — 3 равносильно совокупности систем: ______________
Уравнение |x| = 2 равносильно совокупности уравнений __________
Уравнение |х2 — 2х — 2| = x — 1 равносильно совокупности двух систем _______________
Уравнение х2 — 2х = x – 2 имеет корни, равные
Уравнение х2 — 4х + 3 = 2х – 5 _______________ корень(ня, ей)
Уравнение х2 — 4х + 3 = 2х – 5 имеет два корня, равные: ______
Уравнение х2 – x — 6 = 0 имеет два корня: _________
Уравнение х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1) имеет единственный корень х1= __
Уравнение, ______________ системе, — уравнение такое, что каждое его решение является решением системы, а каждое решение системы является решением уравнения
Уравнение, ______________ совокупности нескольких систем — уравнение такое, что любое его решение является решением хотя бы одной из этих систем, а любое решение каждой из систем является решением уравнения
Уравнение: равносильно системе
Уравнение: равносильно системе ____________
Уравнение: f(x) = g(x) является следствием уравнения logaf(x) = logag(x) при ____________________
Уравнение: равносильно совокупности систем ______________, где М1 — область существования функции f1(x), а М2 — область существования функции f2(x)
Уравнение: имеет ______________ корень(я)
Уравнение: имеет корень, равный ____
Уравнение: _______________ решение(я, й)
Уравнение: равносильно совокупности систем _______________.
Уравнение: _______________
Уравнение: равносильно совокупности систем: _______________
Уравнение: , являющееся следствием уравнения имеет корень ___, посторонний для уравнения
Уравнение: ____________ является следствием уравнения log2(x — l) + log2(x + l) = 3
Уравнение: ______________ является следствием уравнения х2 + log2(x3 + x — l) = x + 6 + log2(х3 + x — 1)
Уравнения 2log2x = 1 и log2x2=1 являются равносильными на множестве всех ___________ чисел
Уравнения и х2 = 1 ____________________ чисел
Уравнения =1 и х2=1 являются равносильными на множестве всех ___________ чисел
Уравнения, _____________ на множестве М – два уравнения, такие, что любой корень первого уравнения, принадлежащий множеству М, является корнем второго уравнения, а любой корень второго уравнения, принадлежащий множеству М, является корнем первого уравнения
Уравнения, содержащие неизвестное под знаком корня, — это ______________ уравнения
Функции возрастающие и убывающие называются _________ монотонными функциями
Функция, ____________ на данном промежутке X — функция y = f(x), определенная на промежутке X, для которой для любой пары чисел х1 и х2 из этого промежутка из неравенства х1 f(x2)
Функция, _____________ на промежутке — функция, которая непрерывна в любой точке промежутка
Числовые _____________ — общее название для числовых отрезков, интервалов, полуинтервалов
Чтобы записать систему, обычно записывают друг под другом все входящие в нее уравнения и неравенства и объединяют их слева фигурной скобкой вида: ___
💥 Видео
Уравнение четвертой степениСкачать

Посторонние корни иррационального уравненияСкачать

Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Иррациональные уравнения без проверки.Скачать

Как решать иррациональные уравнения. Методы решения иррациональных уравнений. (часть 1).Скачать

Вспоминаем схему Горнера и уравнения высших степенейСкачать

Возведение в степень произведения и степени. Алгебра, 7 классСкачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Иррациональные уравнения — часть 1Скачать

Дробно-рациональные уравнения. 8 класс.Скачать

Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать