Уравнение спроса на некоторый товар имеет вид p 134 q 2 (4 видео)

Математический анализ Практическая задача № 1 и № 2 – Решение

Дисциплина	Математические
Тип работы	Контрольные
Количество страниц	9
Год сдачи	2017
Номер работы	703

Содержание

О работе
Содержание
Спрос, предложение, равновесие. Многофакторная функция спроса. Избыточный спрос (дефицит). Запись функции спроса и предложения, равновесие
Страницы работы
Содержание работы
Примение аналитическое геометрии и математического анализа в экономики (стр. 2 )
🎥 Видео

О работе

Содержание

Дисциплина Математический анализ
Направление – Экономика
ПРАКТИЧЕСКАЯ ЗАДАЧА № 1
по освоению профессиональных компетенций ПК-1, ПК-2, ПК-6
Задание 1:
Функция издержек имеет вид C(x)=10+x^2/10 .
На начальном этапе фирма организует производство так, чтобы минимизировать средние издержки A(x). В дальнейшем на товар устанавливается цена, равная 4 усл. ед. за единицу. На сколько единиц товара фирме следует увеличить выпуск?
Решение

Задание 2.
Фирма минимизирует средние издержки, которые получаются в результате равными 30 руб./ед. Чему равны при этом предельные издержки?
Решение

Задание 3.
Считается, что увеличение реализации y от затрат на рекламу x (млн. руб.) определяется соотношением :y=0,1√x . Доход от реализации единицы продукции равен 20 тыс. руб. Найти уровень рекламных затрат, при котором фирма получит максимальную прибыль.
Решение

Задание 4.
Зависимость дохода монополии от количества выпускаемой продукции x определяется как D(x)=100x-1000√x (400≤x≤900). Функция издержек на этом промежутке имеет вид :C(x)=50x+4/(5 ) x√x . Найти оптимальное для монополии-производителя значение выпуска продукции.
Решение

ПРАКТИЧЕСКАЯ ЗАДАЧА № 2
по реализации профессиональной компетенции ПК-4,ПК-5,ПК-10,ПК-15.
Задание 1:
Изменение производительности производства с течением времени от начала внедрения нового технологического процесса задается функцией z=32-2^(-0,5t+5) ,где t – время в месяцах. Найти объем продукции, произведенной а) за первый месяц ; б) за третий месяц;
в) за шестой месяц; г) за последний месяц года, считая от начала внедрения рассматриваемого технологического процесса.
Решение

Задание 2.
Найти объем продукции, выпущенной предприятием за год (258 рабочих дней), если ежедневная производительность этого предприятия задана функцией
f(t)=-0,0033 t^(2 )-0,089 t+20,96 , где 1≤t≤8 -время в часах.
Решение

Задание 4.
Уравнение спроса на некоторый товар имеет вид p=134- x^(2 ).
Найти выигрыш потребителей, если равновесная цена равно 70.
Решение

Вы можете убедиться в качестве данной работы. Часть контрольной представлена ниже:

Видео:Спрос и предложение разбор задачСкачать

Спрос, предложение, равновесие. Многофакторная функция спроса. Избыточный спрос (дефицит). Запись функции спроса и предложения, равновесие

Страницы работы

Содержание работы

Задача 1. Функция спроса и предложения, равновесие.

Кривая спроса на туристические рюкзаки в небольшом городе N описывается следующим уравнением:

Где Q_D – объем спроса в месяц, P – цена. Кривая предложения рюкзаков описывается следующим уравнением:

Где Q_S – месячный объем предложения. Каковы равновесные цена и объем товара?

В равновесии объем спроса равен объему предложения, потому можно приравнять правые части уравнений:

Получлили уравнение с одной переменной Р. Упростив, получим 4Р+2Р=600-300.

Отсюда 6Р=300; а Р=50.

Подставим теперь известную величину в уравнение спроса или предложения, и найдем равновесный объем:

Уравнение спроса : Q_D =600-2×50=500.

Уравнение предложения: Q_S=300+4×50=500

Итак, равновесный объем равен 500 рюкзаков, а равновесная цена – 50 руб.

Необходимо переписать наши уравнения относительно Р, т.е. уравнение спроса запишется как 2Р=Q_D+600, или Р= -1/2 Q_D+300, а уравнение предложения как 4Р= Q_S-300, или P=-1/2Q_S-300/4. Точка прсечения графиков сроса и предложения описывает состояние равновесия.

Задача 2.Многофакторная функция спроса.

Спрос на товар Х описывается формулой:

Где Q- величина спроса на товар X, P- цена товара X, I – доход потребителей,PR – цена на сопряженный товар Y.

А) является ли товар Х нормальным товаром?

Б) являются ли товары X и Y взаимозаменяемыми товарами?

С) на сколько изменится величина спроса, если цена на товар Х возрастет на 2 единицы?

А) нормальным называется товар, спрос на который увеличивается пр росте дохода. Следовательно, если I возрастает, то должна увеличится и величина Q. Действительно, при росте дохода на единицу спрос увеличивается на 0,6,следовательно, товар нормальный.

Б) Два товара называются взаимозаменяемыми, если при росте цены на товар Y спрос на товар Х увеличивается; если с ростом цены на товар Y спрос на товар Х увеличивается, о товары являются взаимодополняющими. В нашем случае, если цена на товар Y вырастет на единицу, то спрос упадет на 5 единиц, следовательно, это два взаимодополняющих товара.

С) Если цена на товар Х возрастетна две единицы, то спрос упадет на 9 единиц.

Задача 3. Избыточный спрос (дефицит)

Если на рынке существует избыточный спрос на товар, то:

Цена на товар превышает равновесную цену;

Товар – низшей категории;

Объем предложения превышает объем спроса;

Цена на товар ниже равновесной цены.

Из графика видно, что если:

А)т.е. цена Р₁, то предложение больше ем спрос (Q₁>Q₀), другими словами, это избыточное предложение;

Б) т.е. товар низшей категории, спрос на который падает с ростом дохода, то это напрямую не влияет на соотношениемежду спросом и предложениемв данном контексте;

Верный ответ г) так как в этом лучае величина спроса (Q₃) , будет превышать величину предложения (Q₄) при цене Р₂ и поэтому возникает избыточный спрос или дефицит.

Задача 4. Запись функции спроса и предложения, равновесие.

При цене светильника 10 руб. величина спроса составляет 100 шт. При увеличении цены на 1 руб. величина спроса уменьшается на 20 светильников. При цене светильников 5 руб. товаропроизводители не готовы выпускать светильники на рынок. Увеличение цены на 1 руб. влечет за собой рост величины предложения на 10 единиц.

1) Определите функции спроса и предложения, предполагая, что эти функции являются линейными.

2) Найдите равновесную цену и равновесное количество выпускаемой продукции.

=20;

=10;

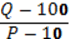
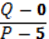
2) Приравняем функции редложения и спроса, иполучим равовесную цену и качество:

Р=11(6) рб. И Q=66(6) шт.

Задача 5. Равновесная цена и равновесный объем, излишек (выигрыш) потребителя и производителя.

Функцию спроса на квашенную капусту имеет вид: Q_D=1000-5P, где Q- количество капусты в день, измеряемое ведрами (в 1 ведро входит 10 кг капусты), а Р- цена капусты в рублях за ведро. Предложение квашенной капусты представлено уравнением: Q_S=4P-80.

1) Определите равновесное количество и равновесную цену. Сколько всего будет потрачено на квашенную капусту? Каков излишек (выигрыш) потребителя в этой точке равновесия? Каков излишек (выигрыш) производителя в этой же точке?

2) Если предположить, что выпуск вынужденно ограничен 300 ведрами в день, о какими будут новые излишек (выигрыш) потребителя и излишек (выигрыш) производителя.каковы будут совокупные птери излишка потребителей и производителей?

Излишек потребителя= ½(200-120)×400=16000 руб.

Излишек производителя = S(120-20)×400=20000 руб.

Совокупный излишек=16000+20000=36000 руб.

Излишек потребителя=1/2(200-140)×300=9000 руб.

Излишек производителя= ½((140-20)+(140-95))×300=24750 руб.

Совокупный излишек=9000+24750=33750 руб.

Чистые потери общества=36000-33750=2250 руб.

Видео:Эластичность спроса и предложения | Как цена влияет на спросСкачать

Примение аналитическое геометрии и математического анализа в экономики (стр. 2 )

Уравнение спроса на некоторый товар имеет вид p 134 q 2

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3

Находим максимум функции T:

T² = -10 0, -1 р0. Найдем выигрыш потребителей от установленной цены р0. Разобьем отрезок [0, х0] на п частей и обозначим точки разбиения:

На каждом интервале выберем точку . Выигрыш потребителей на этом отрезке равен:

где .

Суммируя все выигрыши, получаем:

Если функция спроса непрерывна и п ® ¥, а длина максимального отрезка разбиения max ½Δх½ ® 0, то эта интегральная сумма имеет предел, равный:

Таким образом, выигрыш потребителей:

Аналогично находится выигрыш поставщиков:

Очевидно, что выигрыш потребителей равен площади, заключенной между кривой спроса D и прямой р = ро. Выигрыш поставщиков равен площади, заключенной между прямой р = ро и кривой предложения S (см. рис. 11).

Известны законы спроса и предложения:

Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.

Найдем точку рыночного равновесия:

откуда – не удовлетворяя

Среднее значение. Среднее значение непрерывной функции на промежутке [a, b] находится по формуле

Среднее значение функции используется при вычислении налога на имущество предприятия. Величина налога

где k – коэффициент, зависящий от вида предприятия; f(c) – среднее значение стоимости имущества за год; [a, b] – промежуток времени, равный году.

Интеграл вычисляется приближенно по формуле трапеций с разбиением года на 12 месяцев:

где f(0) – стоимость имущества на 1 января; f(1) – стоимость имущества на 1 февраля; … f(11) – стоимость имущества на 1 декабря; f(12) – стоимость имущества на 1 января следующего года.

Задача максимальной прибыли. В ряде отраслей промышленности, например в горнодобывающей, после некоторого момента времени прибыль начинает убывать. В этом случае необходимо найти момент времени, в который прибыль принимает максимальное значение, и своевременно остановить производство.

Скорости изменения издержек и дохода во времени имеют следующий вид:

Найти максимальное значение прибыли, которое можно получить от этого производства. Когда производство следует остановить?