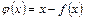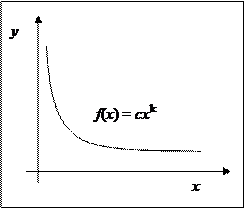ЗАДАНИЕ
Требуется выполнить 10 упражнений по решению экономических задач. Вычисления необходимо проводить средствами пакета MATLAB. Выполненные задания (файлы WORD с решениями и кодом команд MATLAB) просьба сохранить в папку Z:I11COMMONСалтан.
Выигрыш потребителей и выигрыш поставщиков.
Пусть 


Некоторые потребители могут заплатить за товар цену 

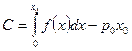
Аналогично находится выигрыш поставщиков:

Очевидно, выигрыш потребителей равен площади, заключенной между кривой спроса D и прямой 

Упражнение 1.
Известны законы спроса и предложения:
Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.
Упражнение 2.
Уравнение спроса на некоторый товар имеет вид:

Найти выигрыш потребителей, если равновесное количество товара равно 10.
Коэффициент неравномерности распределения дохода
Рассмотрим функцию 




На рисунке ниже приведен пример графика функции 
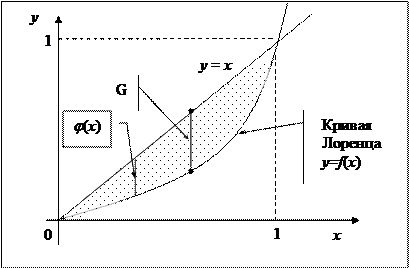
Если бы распределение доходов было совершенным, то 10% населения получали бы 10% совокупного дохода, 20% населения – 20% дохода и т.д. Тогда кривой распределения доходов была бы прямая y=x.
Отклонение реального распределения доходов от идеального измеряется отношением L площади между прямой y=x икривой Лоренца к площади, ограниченной прямыми y=x, x=1 и y=0, и называется коэффициентом неравномерности распределения доходов (коэффициент Джини). Коэффициент Джини (индекс Джини) — статистический показатель, свидетельствующий о степени расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку (например, уровню годового дохода).
Очевидно, что 
Кривые Лоренца применяют для исследования неравномерности распределения не только доходов, но и имущества домохозяйств, долей рынка для фирм в отрасли, природных ресурсов по государствам и т.д.
Кроме коэффициента Джини в экономике используется индекс Робин Гуда (Robin Hood index), также известный как индекс Гувера (Hoover index) — это ещё один показатель неравенства по доходам, имеющий связь с кривой Лоренца. Он равен той доле дохода общества, которую необходимо перераспределить для достижения равенства. Это самый длинный вертикальный отрезок, соединяющий фактическую кривую Лоренца с линией равенства. Обозначим индекс Робин Гуда через G, тогда.

Если, например, индекс Робин Гуда, 
Упражнение 1.
Распределение дохода в некоторой стране определяется кривой Лоренца:

a. Какую часть дохода получают 12% наиболее низко оплачиваемого населения?
b. Подсчитать коэффициент неравномерности распределения совокупного дохода.
c. Какую часть дохода получают 5% наиболее высоко оплачиваемого населения?
d. Чему равен индекс Робин Гуда.
Упражнение 2.
Распределение дохода в некоторой стране определяется кривой Лоренца: 
Какую часть дохода получают 8% наиболее низко оплачиваемого населения? Подсчитать коэффициент неравномерности распределения совокупного дохода. Какую часть дохода получают 4% наиболее высоко оплачиваемого населения. Чему равен индекс Робин Гуда?
Функция обучения
После выпуска определенной партии продукции (изделий) возникает необходимость оценить, сколько времени потребуется для производства некоторого дополнительного количества продукции. Для подобных расчетов пользуются так называемой функцией обучения.
Функция обучения 

Обычно используются функции вида:
где c – затраты времени на первое изделие;

Очевидно, функция 
Среднее время, затрачиваемое на изготовление одного изделия за период освоения от a до b (т.е. от изделия с номером a до изделия с номером b) найдется в соответствии с теоремой о среднем:
Время 


Упражнение 1.
После сборки первой партии изделий было установлено, что время убывает в соответствии с формулой:
Найти время, которое потребуется для сборки изделий в период освоения от a=100 до b=121 и среднее время сборки одного изделия за данный период.
Упражнение 2.
Найти среднее время, затраченное на освоение одного изделия в период освоения от a=30 до b=80 изделий, полагая в функции обучения c=20, k=-0,312.
Видео:Как спрос и предложение задают ценыСкачать

Примение аналитическое геометрии и математического анализа в экономики (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
Находим максимум функции T:
T² = -10 0, -1 р0. Найдем выигрыш потребителей от установленной цены р0. Разобьем отрезок [0, х0] на п частей и обозначим точки разбиения:

На каждом интервале выберем точку 
где 
Суммируя все выигрыши, получаем:

Если функция спроса непрерывна и п ® ¥, а длина максимального отрезка разбиения max ½Δх½ ® 0, то эта интегральная сумма имеет предел, равный:



Аналогично находится выигрыш поставщиков:

Очевидно, что выигрыш потребителей равен площади, заключенной между кривой спроса D и прямой р = ро. Выигрыш поставщиков равен площади, заключенной между прямой р = ро и кривой предложения S (см. рис. 11).
Известны законы спроса и предложения:

Найти выигрыш потребителей и выигрыш поставщиков, если было установлено рыночное равновесие.
Найдем точку рыночного равновесия:
откуда 
Среднее значение. Среднее значение непрерывной функции на промежутке [a, b] находится по формуле
Среднее значение функции используется при вычислении налога на имущество предприятия. Величина налога
где k – коэффициент, зависящий от вида предприятия; f(c) – среднее значение стоимости имущества за год; [a, b] – промежуток времени, равный году.
Интеграл вычисляется приближенно по формуле трапеций с разбиением года на 12 месяцев:
где f(0) – стоимость имущества на 1 января; f(1) – стоимость имущества на 1 февраля; … f(11) – стоимость имущества на 1 декабря; f(12) – стоимость имущества на 1 января следующего года.
Задача максимальной прибыли. В ряде отраслей промышленности, например в горнодобывающей, после некоторого момента времени прибыль начинает убывать. В этом случае необходимо найти момент времени, в который прибыль принимает максимальное значение, и своевременно остановить производство.
Скорости изменения издержек и дохода во времени имеют следующий вид:
Найти максимальное значение прибыли, которое можно получить от этого производства. Когда производство следует остановить?
Видео:Равновесная цена | Крест МаршаллаСкачать

Задачи с решениями
Задача 1.1. В условной экономической системе производится два вида продукции: X и У. Для производства 1 ед. продукции X требуется 50 ед. ресурса, продукции У — 25 ед. Общий объем полностью взаимозаменяемого ресурса, которым располагает экономическая система, составляет 400 ед.
Определите альтернативные издержки производства последней единицы продукта X.
Прежде всего отметим, что альтернативные издержки на изготовление любой единицы продукции, как X, так и У, неизменны, поскольку ресурс, из которого они изготавливаются, полностью взаимозаменяем. Принимая это во внимание, рассчитаем объемы (количества) выпуска продукции обоих видов, разделив величину располагаемого объема ресурса (400 ед.) на соответствующие нормативы его затрат для изготовления продукции X и У. В результате получим 8 ед. продукции X и 16 ед. продукции У. Далее, используя определение альтернативных издержек (количество другого вида продукции, которым необходимо пожертвовать для увеличения объема производства данной продукции на единицу), рассчитаем искомые альтернативные затраты, связанные с изготовлением последней единицы продукции X: 16/8 = 2 ед. продукции У.
Задача 1.2. Самолетом из города А в город В можно добраться за 1 ч, а автобусом — за 5 ч. Стоимость билета на самолет 500 ден. ед., на автобус — 100 ден. ед.
Рассчитайте минимальный часовой заработок, начиная с которого выгодным станет передвижение (в рабочее время) на самолете.
Так как экономические издержки представляют собой сумму явных (бухгалтерских) затрат, а также альтернативных издержек упущенных возможностей, условие равновыгодности рассматриваемых вариантов передвижения из одного города в другой может быть записано так: 500 + х = 100 + 5х, где х — часовой заработок «путешественника».
Значит, передвижения на самолете становится экономически целесообразным, если часовой заработок превышает 100 ден. ед.
Задача 1.3. У фермера три поля, каждое из которых однородно, хотя их урожайность неодинакова. Па этих полях выращивают пшеницу и картофель. На первом поле фермер может вырастить либо 40 т пшеницы, либо 100 т картофеля, на втором — 100 и 150 соответственно, а на третьем — 50 и 100.
Постройте кривую производственных возможностей фермера.
Чтобы построить кривую производственных возможностей фермера, необходимо рассчитать альтернативные издержки, связанные с выращиванием пшеницы и картофеля. Расчеты целесообразно представлять в табличной форме, которая для рассматриваемого примера будет иметь следующий вид.
Третье поле (III)
На оси абсцисс отложим объемы выращиваемого картофеля, а на оси ординат — пшеницы. Тогда, с учетом положений закона возрастания альтернативных издержек, а также производительности соответствующих полей кривая производственных возможностей фермера будет иметь следующий вид.
Задача 1.4. Предположим, что в небольшой мастерской по пошиву брюк работают два человека: мастер и его помощник.
Производительность их труда на раскрое и пошиве брюк (при одинаковом качестве работы) такова:
Затраты времени на ед. товара, ч
Без разделения труда за месяц (120 ч рабочего времени) в мастерской может быть пошито 28 брюк (20 мастером и 8 помощником).
Каким должно быть разделение груда между мастером и помощником, чтобы минимизировать объем выпуска продукции в мастерской?
Работники должны специализироваться в соответствии с принципом сравнительных преимуществ, определяемых по минимуму альтернативных издержек
на выполнение рассматриваемых работ.
Результаты расчета для данного примера приведены ниже.
Помощник должен заниматься раскроем (12 брюк за месяц). За эго же время мастер сможет раскроить 18 и пошить 30 брюк.
Итак, только за счет оптимального распределения обязанностей производительность труда в мастерской выростет на 7% (30 брюк вместо 28).
Задача 1.5. Спрос и предложение конкретного товара в некоторой слаборазвитой стране характеризовались аналитическими зависимостями Q D = 200 — Р и (I s = = -100 + 2 Р.
Правительство страны в целях защиты беднейших слоев населения зафиксировало цену данного товара на уровне ниже равновесного. Результатом этих действий правительства стало сокращение расходов населения на приобретение рассматриваемого товара на 28%.
Определите уровень цены, зафиксированный правительством.
Найдем исходное равновесное состояние рынка рассматриваемого товара и соответствующие ему расходы потребителей:
В условиях зафиксированной цены (/-*,) расходы потребителей данного товара, а значит, и доходы его производителей составили 72 000 ден. ед.
Определяя объем предложения товара в рассматриваемых условиях как 72 000/Р,, запишем уравнение 72 000/Р, = -100 + 2Р,, решая которое, находим: Р, = 90 ден. ед.
Задача 1.6. Функция спроса на некоторый товар имеет вид (У > = 400 — ЮР. Функция предложения данного товара имеет линейный характер, а равновесный объем продаж равен 100 ед. продукции. Известно также, что в рассматриваемых условиях выигрыш потребителей в 2 раза превышает выигрыш производителей.
Определите величину дефицита (перепроизводства) продукции, если на товар будет установлен фиксированный уровень цен — 28 ден. ед.
Решение данной задачи целесообразно проиллюстрировать при помощи графической модели, представленной ниже.
Потребительский излишек соответствует площади треугольника РеР2Е и может быть определен так: 0,5(Р2 — РЕ) • 100. В свою очередь равновесная цена РЕ может быть найдена из уравнения 400 — 10Pf = 100, в результате РЕ = 30 ден. сд. Р2 можно рассчитать аналогично: 400 — 10Р2 = 0, откуда Р2 = 40 ден. ед.
Потребительский излишек составит, таким образом, 500 ден. ед. Из формулы расчета излишка производителей, равного 250 ден. ед., найдем: 1 = 25 ден. ед. : : 0,5(PE-Pt) ? 100 = 250.
Далее определим параметры функции предложения Q v = а + ЬР, используя для этого систему уравнений:
В результате получим (Р = -500 + 20Р.
Так как результатом фиксирования цены Р на уровне 28 ден. ед. станет возникновение дефицита, определим его по формуле:
Задача 1.7. Функции спроса и предложения для некоторого товара имеют вид Q n = 1000 — 5Р и 0 s = -100 + 2,5Р.
В результате фиксирования цены товара возник дефицит, для устранения которого были приняты меры по увеличению предложения данного товара на 100%.
Определите объем (в единицах продукции) устраненного дефицита.
Воспользуемся графической иллюстрацией решения, представленной ниже и в значительной степени облегчающей понимание его процесса.
- 1) Q 5 i =2Q S = -200 + 5Р;
- 2) 1000 — 5Р = -200 + 5Р, Р = 120, Q = 400;
- 3) дефицит = Q D — Q s =1100- 7,5Р= 1100 — 7,5 • 120 = 200 ед. продукции.
Задача 1.8. Функции спроса и предложения на конкретный товар имеют вид: Q° = 8 — Р и 0 s = -4 + 2Р.
Определите, как изменится равновесный объем продаж, если на товар вводится налог в размере 30% от цены, который уплачивает (вносится в бюджет) производитель.
Равновесный объем продаж товара до введения на него налога определим из уравнения 8 — Р = -4 + 2Р, откуда Рравн = 4, QpaBll = 4.
Функция предложения данного товара после введения на него налога примет вид: Q‘ 9 i = -4 + 2(Р-0,ЗР).
Приравняв функцию предложения функции спроса, найдем объем продаж товара в условиях его налогообложения: он составит 3 сд., т.е. уменьшится на 25%.
Задача 1.9. Сирое на некоторый товар характеризуется уравнением Q D = 120 — Р, а предложение этого же товара — уравнением Q s = -30 + 2Р.
Определите, какой минимальный налог на единицу продаваемого товара необходимо установить, чтобы получить в государственный бюджет 600 ден. ед.
Обозначив через N искомый размер налога, определим цену единицы товара в условиях налогообложения: 120 — Р = -30 + 2(Р — N), откуда Р = 50 + 2/3N.
Подставив в найденное выражение P(N) в функцию Q D , найдем: Q(N) = = 70 — 2/3N. Общая сумма налога в этом случае: (70 — 2/3N) • А7 = 600. Решив данное уравнение, найдем: N= 9,4.
Задача 1.10. Рынок некоторого товара характеризуется следующими функциями спроса и предложения: Q D = 740 — 2Р и Q? = -100 + Р.
Правительство установило на данный товар единый налог, максимизирующий общий объем налоговых поступлений в государственный бюджет.
Определите, какая часть налогового бремени легла на плечи потребителей рассматриваемого товара.
Алгоритм решения данной задачи может быть следующим:
1) определим равновесную цену в условиях налога (N):
2) рассчитаем объем продаж:
3) определим размер налога:
4) установим равновесную цену в условиях отсутствия налога:
5) определим размер переплаты за каждую единицу товара, покупаемую потребителями в условиях уплаты налога:
6) рассчитаем общее налоговое бремя потребителей рассматриваемого товара:
Задача 1.11. Функции спроса и предложения для товара, производители (продавцы) которого облагаются единым по величине налогом, установленным на каждую единицу товара, имеют вид: Q D = 800 — 3Р и Q s = -250 + 2Р.
Общий объем налоговых поступлений в государственный бюджет составляет в рассматриваемых условиях 4250 ден. ед.
Определите, на сколько единиц возрастет объем предложения данного товара при отмене введенного на него налога.
Рассматриваемая задача может быть решена в следующей последовательности:
1) определим параметры равновесия в условиях налогообложения товара:
2) рассчитаем величину налога:
3) получим уравнение функции предложения после отмены налога:
4) определим параметры равновесия после отмены налога:
5) рассчитаем прирост объема продаж рассматриваемого товара после отмены на него налога:
Задача 1.12. Рынок некоторого товара, функционирующий в условиях налогообложения его производителей, характеризуется функцией спроса с единичной ценовой эластичностью и функцией предложения: Q 51 = -20 + 2Р. Равновесный объем продаж при этом составлял 10 ед. товара. При отмене налога цена товара сократилась на 1/3. Каким будет объем продаж данного товара после отмены на него налога?
Рассмотрим графическую иллюстрацию данной задачи.
- 1. Определим равновесную цену товара в условиях уплаты налога: 10 = -20 + + 2Р, откуда Р = 15.
- 2. После отмены налога на товар цена снизилась на 10 ден. ед.
- 3. Так как для всех точек единичной функции спроса PQ = const, находим объем продаж в условиях отмены налога: 15 ед. продукции.
Задача 1.13. Предельные полезности для товаров Л, В и С равны соответственно 10, 20 и 18 ед. Известны также цены товаров Л и С: РА = 5 ден. ед., Рс = 9 ден. ед.
При каком уровне цены товара В потребитель будет находиться в положении равновесия?
В состоянии равновесия отношения предельных полезностей к ценам соответствующих товаров должны быть равны. В нашем случае должно выполняться условие
откуда следует, что Рв= 10 ден. ед.
Задача 1.14. Функция полезности потребителя имеет вид: U(A, В, С) = 6а + + 8b + 4с. Известны цены товаров А и В: Рл = 3 ден. ед., Рв = 4 ден. ед.
Определите цену товара С, если потребитель находится в положении равновесия.
Предельная полезность равна частной производной полезности данного товара, следовательно, Mf/4 = б, MUB = 8 и MUC = 4.
Тогда согласно условию равновесия потребителя
Задача 1.15. Определите выбор потребителя, если известны: функция полезности U = 2XY, где X, Y — объемы товаров; цены товаров Рх = 8 ден. ед., PY= 5 ден. ед.; располагаемый доход М = 96 ден. ед.
Необходимо найти такие количественные значения X и Y, при которых функция полезности достигает максимума при заданных бюджетных ограничениях. Последовательность решения задачи может быть следующей:
1) определим предельные полезности товаров:
2) формализуем уравнение бюджетного ограничения:
3) сделаем формализованную запись принципа равновесного состояния потребителя:
4) решим систему уравнений:
Ответ: X = б, У =9,6, 17= 115,2.
Задача 1.16. Спрос на некоторый условный товар характеризуется функцией Q» = 60 — 3Р.
Равновесное состояние рынка данного товара соответствует точке с единичной эластичностью спроса по цене. Известно также, что ценовая эластичность предложения в точке равновесия E s = 1 2 /з- Правительство решило зафиксировать цены на уровне 8 ден. ед.
Определите, что будет наблюдаться в рассматриваемой экономической системе.
Определим координаты точки равновесия:
Найдем параметры функции предложения Q s = а + ЬР> используя формулу расчета точечной эластичности предложения:
Для наших исходных данных получим 5 /3 = 6 10 /30» откуда b = 5.
Определим параметр а: 30 = а + 5 • 10, откуда а = -20.
Итак, функция предложения имеет вид Q s = -20 + 5Р.
Поскольку цена зафиксирована на уровне ниже равновесного, будет иметь место дефицит, объем которого следует рассчитать так:
Задача 1.17. Известно, что функции спроса и предложения на некоторый товар линейны, а кроме того, функция предложения проходит через начало координат и точку с единичной ценовой эластичностью спроса.
Пределите, что будет наблюдаться в рассматриваемой экономической системе.
Для линейной функции спроса (Q? = а — ЬР) координаты точки с единичной эластичностью составляют
Тогда наклон кривой предложения, проходящей но условиям задачи через данную точку, равен
Для линии спроса
Поскольку выполняется условие, можно сделать вывод об индифферентности рынка данного товара.
Задача 1.18. Рынок некоторого товара, функционирующий в условиях налогообложения его производителей, характеризуется функцией спроса с единичной ценовой эластичностью и функцией предложения 0 s = -20 + 2Р. Равновесный объем продаж при этом 10 ед. товара.
При отмене налога предложение товара возросло на 15 ед. для любого уровня цены. Каким будет объем продаж данного товара после отмены на него налога?
Решение данной задачи проиллюстрируем при помощи графической модели.
1. Определим равновесную цену товара в условиях налога:
2. Определим равновесное количество товара в условиях отмененного налога: Qe= 15 • 10/РЕ.
3. Решим уравнение 
Рис. к задаче 1.18
Задача 1.19. Спрос на конкретную продукцию может быть формализован при помощи уравнения Q D = 600 — 2Р.
Выручка производителей (продавцов) дайной продукции составила 45 000 ден. ед.
Определите коэффициент ценовой эластичности спроса, обусловивших указанный размер выручки производителей продукции.
Выручка производителей (продавцов) данной продукции может быть рассчитана так: PQ = Р(600 — 2Р) = 45 000, откуда Р = 150 и Q = 300.
Задача 1.20. Рыночное равновесие некоторого товара с равновесной ценой Р = =100 ден. ед. и равновесным количеством продаж Q = 400 ед. характеризуется эластичностью спроса по цене, равной Е° = -0,5. Известно, что функция спроса на рассматриваемый товар линейна.
Определите максимально возможный объем выручки, который мог бы получить производитель данной продукции в условиях монополизации им рынка рассматриваемого товара.
Для решения данной задачи необходимо определить параметры в явном виде не заданной функции спроса: Q D = а — ЬР. Сделать это можно следующим образом.
1.
2. 400 = а — 2 • 100, следовательно, а = 600.
Задача 1.22. Определите точечную эластичность спроса на товар по его цене, если известно, что уменьшение цены на 5% привело к снижению выручки на 2%.
Используем символы Р, Q и PVQV обозначающие цены и количества до и после изменения цены товара.
Тогда на основании исходных данных можно записать:
Разделим обе части уравнения па PQ и после несложных арифметических преобразований получим AQ/Q = 0,0316.
Тогда
🎥 Видео
2.3 Рыночное равновесиеСкачать

Спрос, предложение и общественное благосостояниеСкачать

Функция потребленияСкачать

Спрос и предложение разбор задачСкачать

Экономика. Теория потребительского выбора. Вывод функции спроса на товарСкачать

2.1 Спрос и величина спросаСкачать
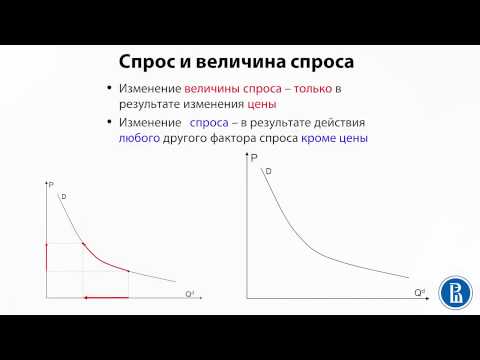
Олимпиадная экономика. Спрос и предложение. Уровень Хард - Курс Пси 22/23 - Неделя 1 - ЛекцияСкачать

Доход потребителя, закон и эластичность спросаСкачать

Потребительский поиск. Лекция 3 (Азамат Кашакбаев)Скачать

Спрос и предложение. Олмат.Экономика.Скачать

Спрос, предложение и анализ основных моделей рыночного равновесияСкачать

#19 Тесты по экономике, часть 2.1 тема: эластичность спроса и предложенияСкачать

Как решать задачи Регионального этапа ВСОШ по экономикеСкачать

Разбор регионального этапа ВСОШ 2023. Экономика. 9 классСкачать

Урок 28. Экономика. Решение экономических задач.Скачать

ЭКОНОМИКА ОЛИМПИАДЫ. Вся необходимая теория для муниципального этапаСкачать

Олимпиадная Экономика 2020. Кривая торговых возможностей (КТВ), построение.Скачать

Все тесты ВСОШ за 3 часа! ЭкономикаСкачать