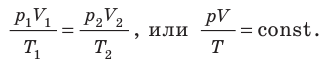Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение состояния идеального газа
- Уравнение состояния идеального газа
- Термодинамические параметры газа
- Объединенный газовый закон. Приведение объема газа к нормальным условиям
- Молярная газовая постоянная. Определение числового значения постоянной Больцмана
- Уравнение Клапейрона — Менделеева. Плотность газа
- Зависимость средней квадратичной скорости молекул газа от температуры
- Изохорический процесс
- Изобарический- процесс
- Изотермический процесс
- Внутренняя энергия идеального газа
- Работа газа при изменении его объема
- Идеальный газ. Формула концентрации молекул газа. Пример задачи
- Идеальный газ
- Универсальное уравнение
- Понятие о концентрации молекул: виды концентраций
- Формула концентрации молекул газа
- Пример задачи
- 📸 Видео
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение состояния идеального газа
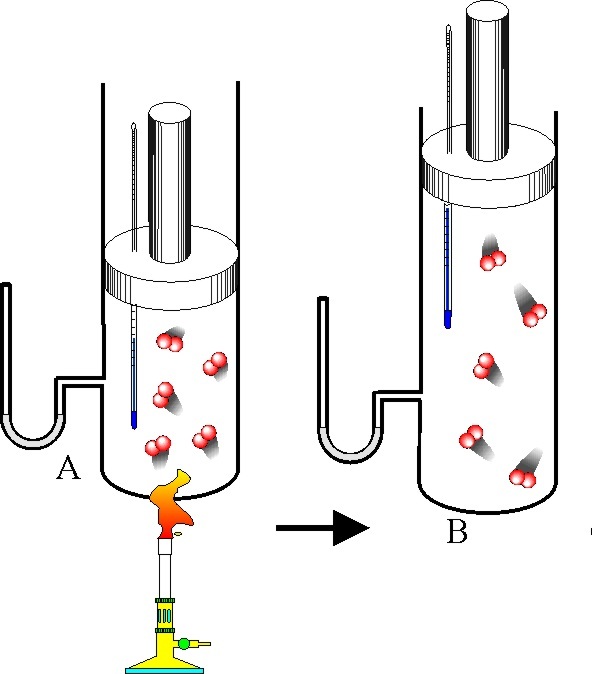
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 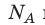
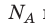
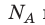
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
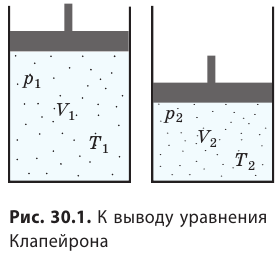
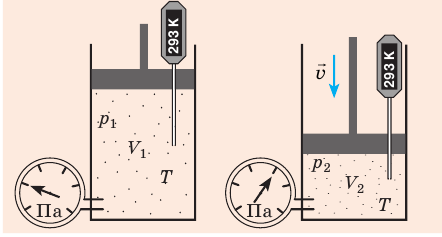
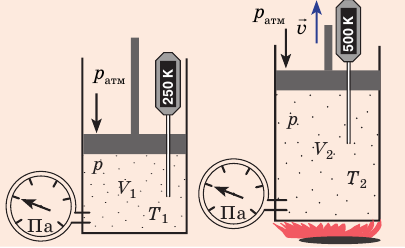
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (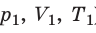
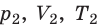
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 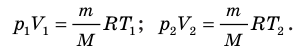
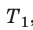
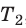
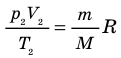
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (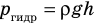
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (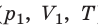
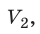
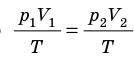
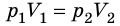
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 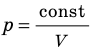
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (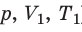
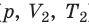
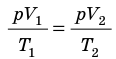
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
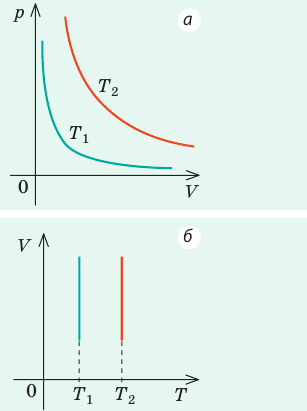
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (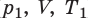
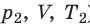
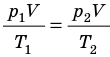
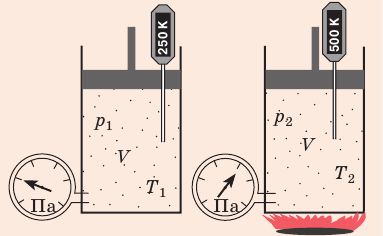
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
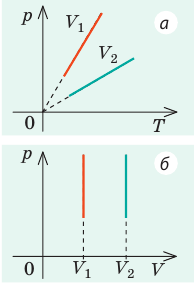
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 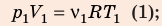
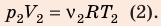

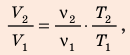
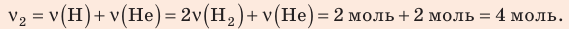
Ответ: примерно в 2,7 раза.
Пример №2
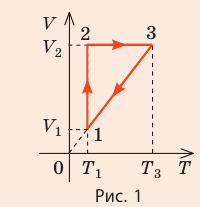
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
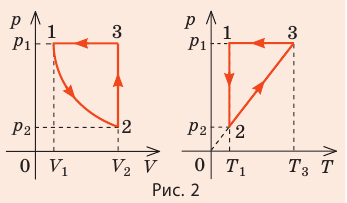
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа
Содержание:
Уравнение состояния идеального газа получило название «уравнение Менделеева-Клапейрона». Давление смеси химически невзаимодействующих газов равно сумме их парциальных давлений: закон Дальтона.
На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение состояния идеального газа
Уравнение состояния идеального газа — это p = nkT называется уравнением Менделеева Клапейрона и оно даёт взаимосвязь трёх важнейших макроскопических параметров, описывающих состояние идеального газа давления, объёма и температуры. Поэтому уравнение Менделеева Клапейрона называется ещё уравнением состояния идеального газа.
Термодинамические параметры газа
В предыдущих главах было показано, что при описании свойств газа можно пользоваться величинами, характеризующими молекулярный мир (микромир), например энергией молекулы, скоростью ее движения, массой и т. п. Числовые значения таких величин мы можем определять только с помощью расчета. Все такие величины принято называть микроскопическими (от греческого «микрос» — малый).
Однако для описания свойств газов можно пользоваться и такими величинами, числовые значения которых находят простым измерением с помощью приборов, например давлением, температурой и объемом газа. Значения таких величин определяются совместным действием огромного числа молекул, поэтому они называются макроскопическими (от греческого «макрос» — большой).
Соотношение (4.1): 
Если взять определенную массу газа т, то при постоянных р, V и Т газ будет находиться в равновесном состоянии. Когда происходят изменения этих параметров, то в газе протекает тот или иной процесс. Если этот процесс состоит из ряда непрерывно следующих друг за другом равновесных состояний газа, то он называется равновесным процессом. Равновесный процесс должен протекать достаточно медленно, так как при быстром изменении параметров давление и температура не могут иметь соответственно одинаковые значения во всем объеме газа. В этой главе рассматриваются только равновесные процессы в газах, при которых масса газа остается постоянной.
Когда процесс в газе заканчивается, то газ переходит в новое состояние, а его параметры приобретают новые постоянные числовые значения, вообще говоря, отличные от их значений в начале процесса. Если же при постоянной массе газа значения всех его параметров в начале и в конце процесса окажутся одинаковыми, то процесс называется круговым или замкнутым.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом. Газовый закон, выражающий связь между всеми тремя параметрами газа, называется объединенным газовым законом.
Отметим еще, что такого процесса в газе, при котором изменялся бы только один параметр газа, не существует, так как значения этих параметров взаимосвязаны. Примером сказанного является закон Шарля, выражающий связь между р и Т.
Объединенный газовый закон. Приведение объема газа к нормальным условиям
Связь между давлением, объемом и температурой определенной массы газа устанавливается с помощью соотношения (4.9):
Поскольку 

Так как при постоянной массе газа N остается неизменным, 
Поскольку значения р, V и Т в (5.2) относятся к одному и тому же состоянию газа, можно следующим образом сформулировать объединенный газовый закон: при постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Следовательно, если числовые значения параметров в начале процесса, происходящего с какой-либо определенной массой газа, обозначить через р1 , V1 и Т1, а их значения в конце процесса соответственно через р2 , V2 и Т2, то
Формулы (5.2) и (5.3) представляют собой математическое выражение объединенного газового закона.
На практике иногда нужно установить, какой объем V0 займет имеющаяся масса газа при нормальных условиях, т. е. при Т0=273 К и при р0=1,013 . 10 5 Па. Если значения параметров для этой массы газа в каком-либо произвольном состоянии, отличном от нормального, обозначить через р, V и Т, то на основании (5.3) получаем 
Формула (5.4) позволяет приводить объем заданной массы газа к нормальным условиям.
Молярная газовая постоянная. Определение числового значения постоянной Больцмана
Формула (5.1) справедлива для любой массы газа, в которой содержится N молекул. Если применить эту формулу к одному молю какого-либо газа, то N нужно заменить постоянной Авогадро NA, а V — объемом одного моля Vмоль
Так как в одном моле любого газа содержится одно и то же число молекул NA, то произведение 

Числовое значение R можно найти, если применить (5.5) к состоянию одного моля газа при нормальных условиях, так как при этом 
Это числовое значение R в СИ необходимо запомнить, так как им часто пользуются при расчетах и при решении задач.
Теперь легко найти числовое значение постоянной Больнмана 



Уравнение Клапейрона — Менделеева. Плотность газа
Выясним, как будет выглядеть соотношение (5.1), если в него ввести молярную газовую постоянную R. Так как N — полное число молекул в массе газа т, а 
где 
Поскольку 


Соотношение (5.7) называется уравнением Клапейрона — Менделеева или уравнением состояния для произвольной массы идеального газа. Для одного моля идеального газа уравнение Клапейрона — Менделеева принимает вид
С помощью формулы (5.7) легко выяснить, какими величинами определяется плотность газа. Так как 
Зависимость средней квадратичной скорости молекул газа от температуры
Выясним теперь, как можно с помощью вычислений находить среднюю квадратичную скорость движения молекул газа 



Отметим, что под т в формуле (5.10) подразумевается масса одной молекулы в кг. Так как 



Наконец, из (5.9) следует, что 
Среднюю квадратичную скорость можно находить по любой из формул (5.10)—(5.12). Из функции Максвелла можно получить формулы для средней арифметической скорости и наивероятнейшей скорости. Средняя арифметическая скорость
Наконец, наивероятнейшую скорость вычисляют так:
(Используя график функции Максвелла (рис. 3.3), поясните, почему 


Изохорический процесс
Процессы, при которых масса газа и один из его параметров остаются постоянными, называются изопроцессами (от греческого «изос» — равный, одинаковый). Поскольку имеется три параметра газа, существует три различных изопроцесса. Первый из них (изохорический) рассмотрен выше (§ 4.3). Процесс в газе, который происходит при постоянной массе и неизменном объеме, называется изохорическим (от греческого «хора» — пространство). Графики для этого процесса называются изохорами (рис. 4.3).
Отметим, что к любому изопроцессу применим объединенный газовый закон и формулы (5.3), (5.7) и (5.8) с учетом того, что один из параметров остается постоянным. При изохорическом процессе постоянным остается объем V, поэтому формула (5.3) после сокращения на V принимает вид
Итак, изохорический процесс подчиняется закону Шарля: при постоянной-массе газа и неизменном объеме давление газа прямо пропорционально его абсолютной температуре. Это видно и из уравнения Клапейрона — Менделеева (5.7):
Так как V, т, 
Изобарический- процесс
Процесс в газе, который происходит при постоянной массе и неизменном давлении, называется изобарическим (от греческого «барос» — тяжесть). Этот процесс был изучен французским физиком Л. Гей-Люссаком в 1802 г.
Поскольку при изобарическом процессе р постоянно, то после сокращения на р формула (5.3) принимает вид
Формула (5.16) является математическим выражением закона Гей-Люссака: при постоянной массе газа и неизменном давлении объем газа прямо пропорционален его абсолютной температуре. (Это видно и из уравнения Клапейрона — Менделеева (5.7): так как р, т, 
На рис. 5.1 схематически изображен опыт Гей-Люссака. Колба с газом помещается в сосуд с водой и льдом.
В пробку вставлена трубка, изогнутая таким образом, что свободный конец ее горизонтален. Газ в колбе отделен от окружающего воздуха небольшим столбиком ртути в трубке. Температуру газа определяют по термометру, а объем — по положению столбика ртути. Для этого на трубке нанесены деления, соответствующие определенному внутреннему объему трубки (при градуировке трубки можно учесть и расширение сосуда при нагревании, но оно сравнительно мало’).
Сначала по положению столбика ртути 1 определяют 
Оказывается, что изобара представляет собой прямую линию (рис. 5.2, а), которая пересекается с осью абсцисс в точке А.
Из подобия треугольников на рис. 5.2, а следует
Обозначив 

Здесь 
Если повторять этот опыт для разных газов или для разных масс газа, то все графики будут пересекаться в точке А, соответствующей t=—273°С (рис. 5.2, б), т. е. коэффициент 
Отметим, что для газов коэффициенты 


Изотермический процесс
Процесс в газе, который происходит при постоянной температуре, называется изотермическим.
Изотермический процесс в газе был изучен английским ученым Р. Бойлем и французским ученым Э. Мариоттом. Установленная ими опытным путем связь получается непосредственно из формулы (5.3) после сокращения на Т:
Формула (5.18) является математическим выражением закона Бойля — Мариотта: при постоянной массе газа и неизменной температуре давление газа обратно пропорционально его объему. Иначе говоря, в этих условиях произведение объема газа на соответствующее давление есть величина постоянная: 
Соотношение (5.19) можно получить и из (5.7) или (5.8), так как при постоянном Г справа в формулах (5.7) и (5.8) стоит постоянная величина. График зависимости р от V при изотермическом процессе в газе представляет собой гиперболу и называется изотермой. На рис. 5.3 изображены три изотермы для одной и той же массы газа, но при разных температурах Т.
Отметим еще, что из формулы (5.9) непосредственно вытекает, что при изотермическом процессе плотность газа изменяется прямо пропорционально давлению:
(Подумайте, как проверить закон Бойля — Мариотта на опыте.)
Внутренняя энергия идеального газа
Как отмечалось, силы взаимодействия молекул в идеальном газе отсутствуют. Это означает, что молекулярно-потенциальной энергии у идеального газа нет. Кроме того, атомы идеального газа представляют собой материальные точки, т. е. не имеют внутренней структуры, а значит, не имеют и энергии, связанной с движением и взаимодействием частиц внутри атома. Таким образом, внутренняя энергия идеального газа представляет собой только сумму знамений кинетической энергии хаотического движения всех его молекул:
Поскольку у материальной точки вращательного движения быть не может, то у одноатомных газов (молекула состоит из одного атома) молекулы обладают только поступательным движением. Так как среднее значение энергии поступательного движения молекул определяется соотношением(4.8): 



Для произвольной массы одноатомного идеального газа имеем
Если молекула газа состоит из двух жестко связанных атомов (двухатомный газ), то молекулы при хаотическом движении приобретают еще и вращательное движение, которое происходит вокруг двух взаимно перпендикулярных осей. Поэтому при одинаковой температуре внутренняя энергия двухатомного газа больше, чем одноатомного, и выражается формулой
Наконец, внутренняя энергия многоатомного газа (молекула содержит три или больше атомов) в два раза больше, чем у одно-атомного при той же температуре:
поскольку вращение молекулы вокруг трех взаимно перпендикулярных осей вносит в энергию теплового движения такой же вклад, как поступательное движение молекулы по трем взаимно перпендикулярным направлениям.
Отметим, что формулы (5.23) и (5.24) теряют силу для реальных газов при высоких температурах, так как при этом в молекулах возникают еще колебания атомов, что ведет к увеличению внутренней энергии газа. (Почему это не относится к формуле (5.22)?)
Работа газа при изменении его объема
Физический смысл молярной газовой постоянной. Опыт показывает, что сжатый газ в процессе своего расширения может выполнять работу. Приборы и агрегаты, действия которых основаны на этом свойстве газа, называют пневматическими. На этом принципе действуют пневматические молотки, механизмы для закрывания и открывания дверей на транспорте и т. д.
Представим себе цилиндр с подвижным поршнем, заполненный газом (рис. 5.4).
Пока давление газа внутри цилиндра и окружающего наружного воздуха одинаковы, поршень неподвижен. Пусть при этом температура газа и окружающей среды равна 
Будем теперь медленно нагревать газ в цилиндре до температуры 






Нетрудно сообразить, что при изохорическом процессе работа газа равна нулю, так как никакого изменения объема, занятого газом, в этом случае не происходит. Вообще следует помнить, что газ выполняет работу только в процессе изменения своего объема, т. е. при 


Выясним, как можно определить работу газа по графику зависимости р от V в том или ином газовом процессе. При изобарическом процессе график зависимости р от V представляет собой прямую линию, параллельную оси абсцисс, так как р постоянно. Из рис. 5.5 видно, что работа газа в этом случае численно равна заштрихованной площади.
Выясним, как найти работу газа при изотермическом процессе. На рис. 5.6 изображена изотерма идеального газа. При таком процессе газ выполняет работу, так как 




Разбивая интервал 





Можно строго доказать, что работа газа при любом процессе выражается площадью, ограниченной двумя ординатами, отрезком оси абсцисс и графиком того процесса в координатах V и р.
Выясним теперь физический смысл молярной газовой постоянной R. Применяя формулу (5.25) к одному молю идеального газа, получим
Но из уравнения Клапейрона — Менделеева (5.8) для одного моля можно записать для двух состояний газа:
Подставляя это выражение в (5.26), будем иметь 
Из (5.27) следует, что молярная газовая постоянная численно равна работе, совершаемой одним молем идеального газа при его изобарическом нагревании на один кельвин.
Из соотношения 
Услуги по физике:
Лекции по физике:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Уравнение состояния идеального газаСкачать

Идеальный газ. Формула концентрации молекул газа. Пример задачи
В физике текучих субстанций большое внимание уделяется изучению газов, которое осуществляют при помощи использования модели идеального газа. В этой области было открыто много законов. В приведенной ниже статье изучим формулу концентрации молекул газа (идеального) и покажем, как ее следует применять при решении практической проблемы.
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Идеальный газ
Что же это такое? Прежде чем записать формулу концентрации молекул газа, расскажем, что собой представляет модель идеального газа. В соответствии с кинетической теорией текучих субстанций, в таких веществах молекулы и атомы движутся хаотически по прямым траекториям. Расстояния между ними намного больше, чем их собственные линейные размеры, поэтому последними пренебрегают при выполнении вычислений. Кроме того, считают, что взаимодействий между молекулами не существует, поскольку их кинетическая энергия слишком велика по сравнению со слабыми потенциальными взаимодействиями.
Любые реальные газы, которые находятся при низких давлениях и достаточно высоких абсолютных температурах, по своему поведению приближаются к описанной модели. Тем не менее существуют текучие субстанции, у которых помимо ван-дер-ваальсовых взаимодействий между частицами действуют взаимодействия более сильного характера. Примером является водяной пар, у которого молекулы друг с другом связаны водородными (полярными) связями. Для описания поведения таких субстанций нельзя использовать модель идеального газа.
Видео:10 класс, 4 урок, Уравнение состояния идеального газаСкачать

Универсальное уравнение
Модель идеального газа удобна при выполнении практических расчетов тем, что уравнение состояния вещества, полученное на ее основе, связывает три термодинамических параметра: температуру T, объем системы V и абсолютное давление P. Это уравнение записано ниже:
Где R — постоянная, равная 8,314 Дж/(моль*К), n — количество вещества.
Современная молекулярно-кинетическая теория газов позволяет путем несложных рассуждений и математических выкладок получить теоретически это уравнение. Впервые же оно было записано в результате анализа многочисленных экспериментов, которые в течение двух веков выполняли европейские ученые, начиная от Роберта Бойля (вторая половина XVII века) и заканчивая Амедео Авогадро (начало XIX века).
Считается, что уравнение состояния идеального газа первым получил Эмиль Клапейрон, а к современной форме его привел русский химик Дмитрий Менделеев, поэтому его часто называют законом Клапейрона-Менделеева.
Видео:Уравнение состояния идеального газаСкачать

Понятие о концентрации молекул: виды концентраций
Когда изучают текучие субстанции, то знать концентрации компонентов, которые их образуют, является важным при решении многих практических задач. Например, от этого показателя и размеров молекул зависит общая площадь поверхности активного вещества, а значит, его реакционная способность. Другой пример, концентрация некоторых веществ в воздухе определяет допустимые их пределы для нормального протекания жизненно необходимых процессов в организме человека.
В случае газов, как правило, пользуются тремя следующими концентрациями:
- Атомная. Она определяется, как процентное содержание количества атомов или молекул компонента по отношению к объему всей системы.
- Массовая. Показывает отношение массы компонента к объему газа.
- Молярная. Она равна отношению количества вещества изучаемого компонента к объему системы.
Заметим, что все виды концентраций вычисляются по отношению к объему системы. Справедливость этих величин действительна, поскольку каждый компонент системы полностью заполняет ее объем.
Среди всех типов концентраций наиболее удобной на практике является молярная. Ниже в статье приведем формулу именно для нее.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Формула концентрации молекул газа
В соответствии с приведенным в предыдущем пункте определением, молярная концентрация i-го компонента системы cn(i) вычисляется так:
Предположим, что мы имеем однокомпонентный (чистый) газ. Это может быть кислород, азот, гелий и так далее. В этом случае можно применить формулу Клапейрона-Менделеева и выразить из нее молярную концентрацию молекул. Имеем:
cn = n / V = P / (R * T).
Из записанной формулы концентрации молекул газа легко получить атомную (молекулярную) концентрацию. Покажем, как это делается:
Здесь NA и kB — число Авогадро и постоянная Больцмана. Соответственно, N — число молекул в системе. Поскольку величина kB имеет маленькое значение (1,38 * 10 -23 ), то cN принимает огромные значения, что неудобно для ее практического использования.
Видео:МКТ идеального газа. Уравнения состояния идеального газа | Физика, онлайн-форумСкачать

Пример задачи
В результате изобарного нагрева закрытой системы с идеальным газом его температура увеличилась на 100 К и стала равной 400 К. Как изменится концентрация молекул газа, если давление в системе составляет 1,5 атмосферы.
Поскольку давление в процессе нагрева не изменилось, а температура была равна 300 К согласно условию задачи, то молярная концентрацию молекул до нагрева системы составляла:
cn1 = 1,5 * 101 325 / (8,314 * 300) = 60,9 моль/м 3 .
Число молекул в системе не изменилось при нагреве, так как система является закрытой. После нагрева газа его концентрация составила:
cn2 = 1,5 * 101 325 / (8,314 * 400) = 45,7 моль/м 3 .
Изменение концентрации составило:
Отрицательный знак говорит, что концентрация уменьшилась, что является очевидным, поскольку увеличился объем системы после нагрева, а число частиц в ней осталось прежним.
📸 Видео
Физика 10 класс (Урок№19 - Температура. Энергия теплового движения молекул.)Скачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Урок 146. Основное уравнение МКТ идеального газа - 2Скачать

Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Все формулы молекулярной физики, МКТ 10 класс, + преобразования и шпаргалкиСкачать

Уравнение состояния идеального газа. Газовые законыСкачать

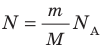
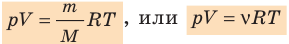
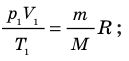
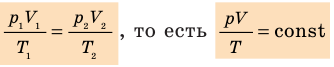
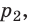
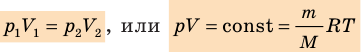

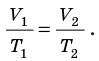
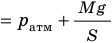
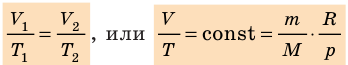
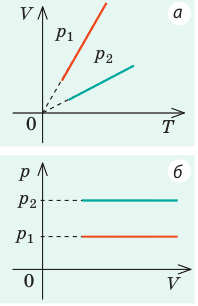

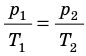
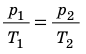
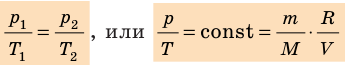

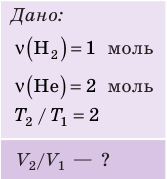
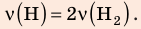

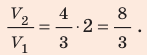
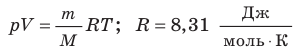 — универсальная газовая постоянная.
— универсальная газовая постоянная.