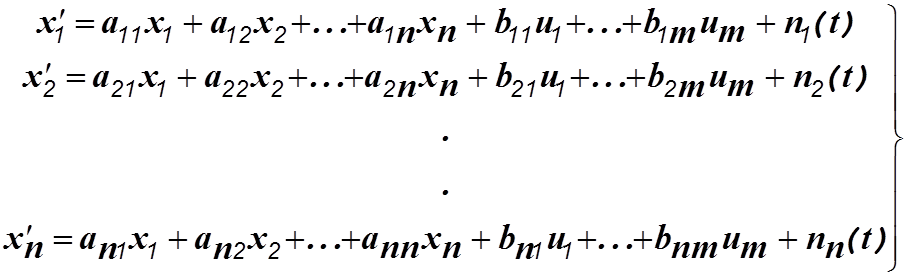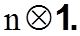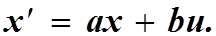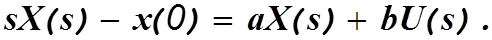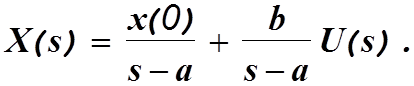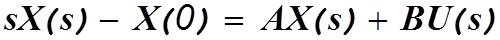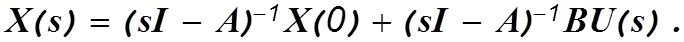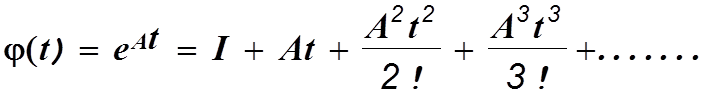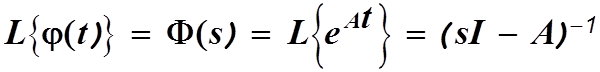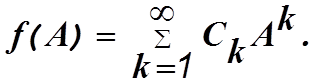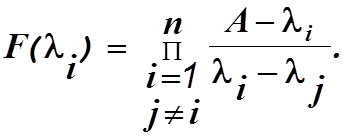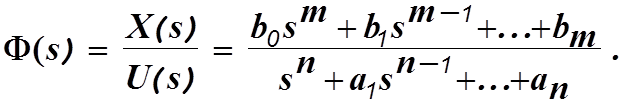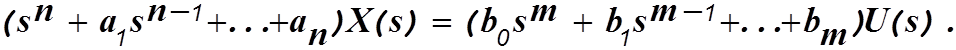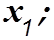Уравнение состояния динамической системы представляет собой

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Основные понятия современной теории управления

Страницы работы

Содержание работы

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

1. Основные понятия современной теории управления.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Оглавление

Видео:Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

1.1. Переменные состояния и уравнения состояния динамической

1.2. Матричная передаточная функция………………………………5

1.3. Понятия управляемости и наблюдаемости системы……………5

1.1. Переменные состояния и уравнения состояния динамической системы.

Состояние динамической системы- это совокупность физических переменных 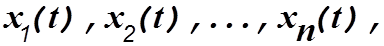характеризующих поведение системы в будущем при условии, что известны ее начальное состояние и приложенные воздействия.

Динамическая система может быть описана системой дифференциальных уравнений первого порядка

Запишем эту систему в матричной форме

(1.1)

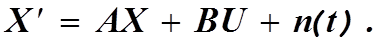
В этом выражении X--матрица параметров (координат) состояния, А-матрица состояния, составленная из коэффициентов системы уравнений, B-матрица управления, U-матрица управляющих воздействий, n(t)-вектор возмущений размерности

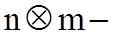
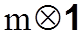
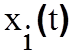
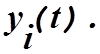
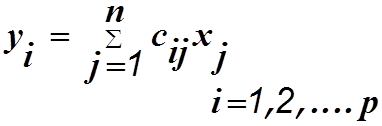
Все или только некоторые параметры состояния для использования в целях управления должны быть измерены приборами специальной измерительной системы. Поэтому для полного описания динамической системы уравнение состояния (1.1) должно быть дополнено уравнением, связывающим переменные состояния и выходные переменные измерительной системы Эти выходные переменные в общем случае являются линейной комбинацией параметров состояния с некоторыми весами и связь между ними выражается системой линейных алгебраических уравнений

(1.2)

В векторно-матричной форме уравнение (1.2) можно записать следующим образом

(1.3)

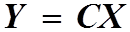
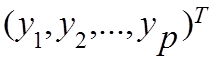
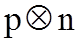
Матрицу столбец Y= называют выходным вектором или вектором наблюдения. Матрица С размера называется матрицей выхода или матрицей наблюдения.

Решение векторно-матричного уравнения (1.1) при n(t)=0 можно найти так же, как и решение обыкновенного дифференциального уравнения 1-го порядка. Рассмотрим обыкновенное дифференциальное уравнение вида

В изображениях по Лапласу получим

Использовав процедуру обратного преобразования Лапласа, получим

(1.4)

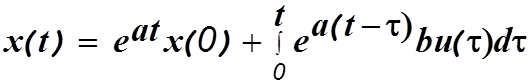
Решение векторного уравнения (1.1) определяется аналогично.

В этом выражении I-единичная матрица. По аналогии с (1.4) запишем

(1.5)

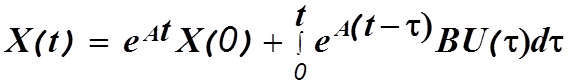
Функция 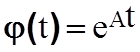называется фундаментальной или переходной матрицей.

Методы вычисления фундаментальной матрицы.

а).Метод разложения в ряд.

Ограничившись конечным числом членов ряда и произведя их суммирование, можно получить приближенное выражение для фундаментальной матрицы.

б).Метод, основанный на определении собственных значений матрицы состояния.

В соответствии с преобразованием Лапласа получим

(1.6)

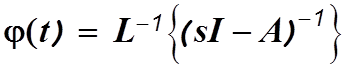
Определение фундаментальной матрицы сводится к вычислению собственных значений матрицы состояния и последующему использованию процедуры обратного преобразования Лапласа.

в).Метод, основанный на теореме Сильвестра.

Предположим, что имеется некоторая функция f(A) от матрицы А, которую можно представить в виде степенного ряда

Допустим, что все собственные числа матрицы А различны. Тогда согласно теореме Сильвестра

где

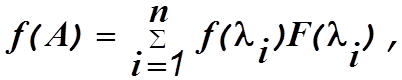
Здесь 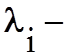собственные числа матрицы состояния А.

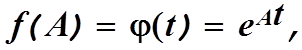
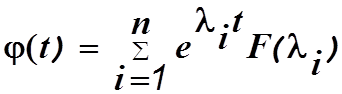
В частном случае, когда получим

(1.7)

После определения фундаментальной матрицы строится решение (1.5).

Часто возникает задача найти описание системы в понятиях пространства состояний, если известна ее передаточная функция в обычном понимании, т.е. в системе “вход-выход”. Пусть эта передаточная функция имеет вид

Дифференциальное уравнение в изображениях по Лапласу будет следующим

Допустим вначале, что m=n.

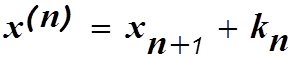
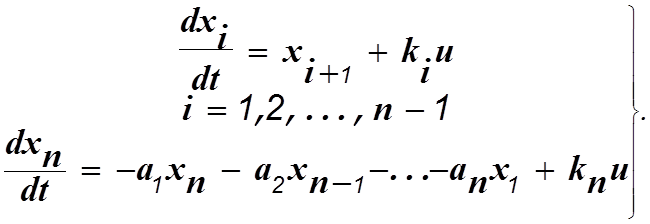
Сделаем замену и перейдем к системе уравнений первого порядка.

(1.8)

Для определения неизвестных коэффициентов 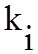проделаем следующие операции:

а) перейдем в системе (1.8) к изображениям по Лапласу при нулевых начальных условиях;

б) найдем характеристический определитель полученной алгебраической системы уравнений;

в)решим эту систему уравнений относительно переменной

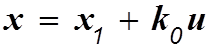
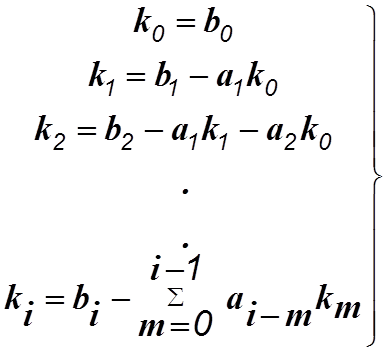
г)учитывая, что найдем выражения для x(s) и, приравнивая числитель полученного выражения числителю исходной передаточной функции, получим рекуррентные соотношения для определения коэффициентов

(1.9)

В практических приложениях всегда m

Видео:Уравнение состояния идеального газаСкачать

Пространство состояний в задачах проектирования систем оптимального управления

Введение

Исследование системы управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа.

Состоянию системы соответствует точка в определённом евклидовом пространстве, а поведение системы во времени характеризуется траекторией, описываемой этой точкой.

При этом математический аппарат включает готовые решения по аналоговому и дискретному LQR и DLQR контролерам, фильтра Калмана, и всё это с применением матриц и векторов, что и позволяет записывать уравнения системы управления в обобщённом виде, получая дополнительную информацию при их решении.

Целью данной публикации является рассмотрение решения задач проектирования систем оптимального управления методом описания пространства состояний с использованием программных средств Python.

Теория кратко

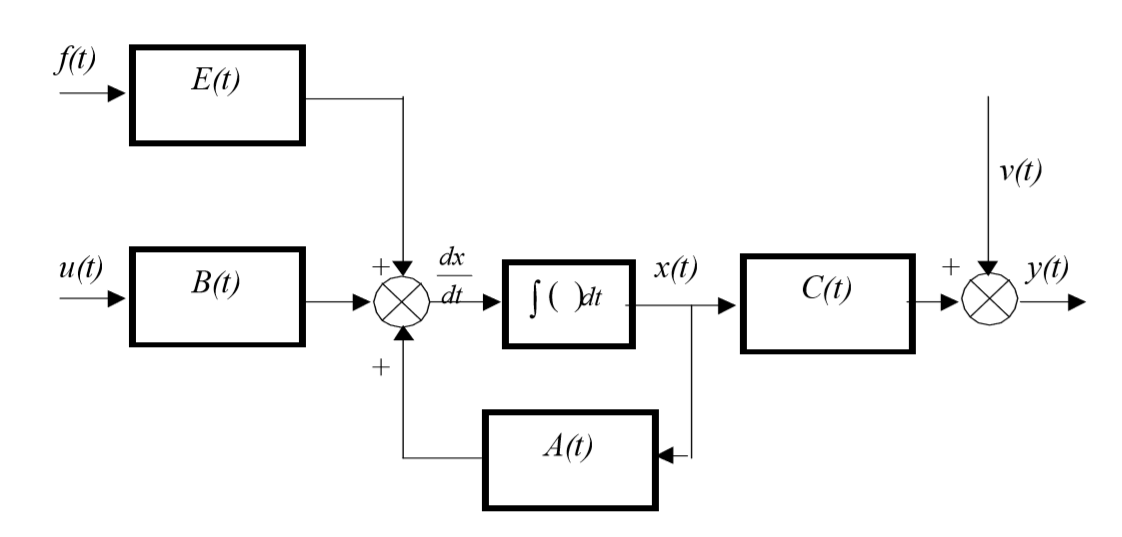
Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:

(1)

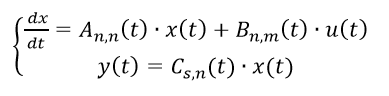
Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным объектом. В противном случае объект будет нестационарным.

При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:

(2)

где y(t) – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).

Структура линейной непрерывной системы, реализующая уравнения (1) и (2), приведена на рисунке:

Данная структура соответствует математической модели объекта, построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).

Для примера рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов. Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть так:

(3)

Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе — условия механического равновесия. В качестве обобщенных координат выберем ток якоря I и частоту вращения якоря ω.

Управлением являются напряжение на якоре U, возмущением — момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см (в системе СИ: Cе=См).

Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.

(4)

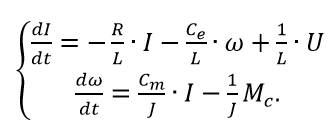
В матричном виде уравнения (4) примут вид (1):

(5)

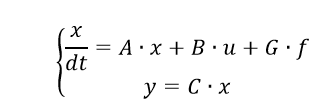
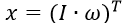
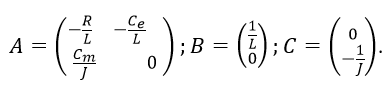
где вектор обобщенных координат , вектор управлений U =u (в рассматриваемом случае он является скаляром), вектор (скаляр) возмущений Mc=f. Матрицы модели:

(6)

Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде:

(7)

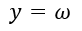
а матрица измерений примет вид:

Сформируем модель двигателя в Python. Для этого вначале зададим конкретные значения параметров двигателя: U = 110 В; R =0,2 Ом; L = 0,006 Гн; J =0,1 кг/м2;Ce =Cm=1,3 В/С и найдем значения коэффициентом матриц объекта из (6).

Разработка программы формирующей модель двигателя с проверкой матриц на наблюдаемость и управляемость:

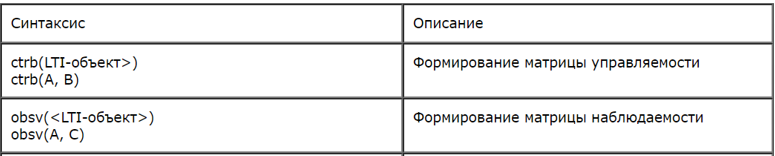
При разработке программы использовалась специальная функция def matrix_rank для определения ранга матрицы и функции, приведенные в таблице:

Результаты работы программы:

Матрица А:
[[ -33.33333333 -216.66666667]
[ 13. 0. ]]
Матрица B:
[[166.66666667]
[ 0. ]]
Матрица C:
[[0 1]]
Скаляр D:
0
Передаточная функция двигателя:
2167/(s^2 + 33.33 s + 2817)
Ранг матрицы управляемости: 2
Ранг матрицы наблюдаемости: 2

1. На примере двигателя постоянного тока с независимым магнитным возбуждением рассмотрена методика проектирования управления в пространстве состояний;

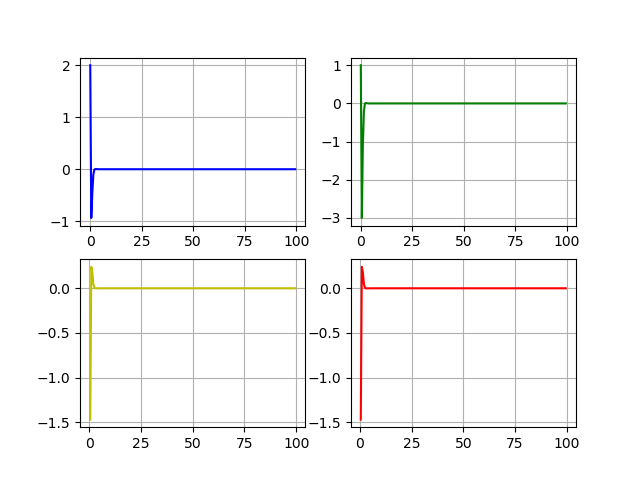
2. В результате работы программы получены передаточная функция, переходная характеристика, а так же ранги матриц управляемости и наблюдаемости. Ранги совпадают с размерностями пространства состояний, что подтверждает управляемость и наблюдаемость модели.

Пример проектирования оптимальной системы управления с дискретным dlqr контролером и полной обратной связью

Определения и терминология

Линейно-квадратичный регулятор (англ. Linear quadratic regulator, LQR) — в теории управления один из видов оптимальных регуляторов, использующий квадратичный функционал качества.

Задача, в которой система описывается линейными дифференциальными уравнениями, а показатель качества, представляет собой квадратичный функционал, называется задачей линейно-квадратичного управления.

Широкое распространение получили линейно-квадратичные регуляторы (LQR) и линейно-квадратичные гауссовы регуляторы (LQG).

Приступая к практическому решению задачи всегда нужно помнить об ограничениях

Для синтеза оптимального дискретного регулятора линейных стационарных систем нужна функция численного решения уравнения Беллмана.Такой функции в библиотеке Python Control Systems [1] нет, но можно воспользоваться функцией для решения уравнения Риккати, приведенной в публикации [2]:

Но нужно ещё учесть ограничения на синтез оптимального регулятора, приведенные в [3]:

• система, определяемая матрицами (A, B) должна быть стабилизируема;
• должны выполняться неравенства S> 0, Q – N/R–N.T>0, пара матриц (Q – N/R–N.T,
  A – B/R–B.T) не должна иметь наблюдаемые моды с собственными значениями на
  действительной оси.

После копаний в обширной и не однозначной теории, которую, по понятным причинам, я не привожу, задачу удалось решить, и все ответы можно прочитать прямо в комментариях к коду.

Структурная схема регулятора системы управления с обратной связью по всем переменным состояния изображена на рисунке:

Для каждого начального состояния x0 оптимальный линейный регулятор порождает оптимальное программное управление u*(x, k) и оптимальную траекторию х*(k).

Программа, формирующая модель оптимального управления с dlqr контролером

K=
[[ 0.82287566 -0.17712434]
[ 0.82287566 -0.17712434]]
P=
[[ 3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E=
[0.17712434+0.17712434j 0.17712434-0.17712434j]

Динамика состояний и управлений: x1, x2, u1, u2.

Вывод

Отдельные задачи оптимального управления по типу приведенных можно решать средствами Python, комбинируя возможности библиотек Python Control Systems, SciPy,NumPy, что, безусловно, способствует популяризации Python, учитывая, что ранее такие задачи можно было решать только в платных математических пакетах.

Видео:Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать

Переменные состояния динамической системы

Анализ и синтез систем управления во временной области основан на понятии состояния системы. Состояние системы—это совокупность таких переменных, знание которых, наряду со входными функциями и уравнениями, описывающими динамику системы, позволяет определить ее будущее состояние и выходную переменную. Для динамиче­ской системы ее состояние описывается набором переменных состояния [ЛГ[(?), X2(t) Х„(0]- Это такие переменные, которые определяют будущее поведение систе­мы, если известно ее текущее состояние и все внешние воздействия. Рассмотрим систему, изображенную на рис. 3.1, где^,^) иy2(t) есть выходные переменные, a ux(t) и u2(t)— вход­ные переменные. Для ЭТОЙ системы переменные (*[, х2. хп) имеют следующий смысл: если в момент времени t0 известны начальные значения [^(fo), x2(t0), . xn(tQ)] и входные сигналы щ(і) и u2(f) для t > t0, то этой информации достаточно, чтобы определить будущие значения всех переменных состояния и выходных переменных.

Структурная схема системы управления

Переменные состояния описывают поведение системы в будущем, если извест­ны текущее состояние, внешние воздействия и уравнения динамики системы.

Общий вид динамической системы приведен на рис. 3.2.

Простым примером переменной состояния может служить положение выключателя электролампочки. Выключатель может быть в одном из двух положений — «включено» или «выключено», поэтому его состоянию соответствует одно из двух возможных значе­ний. Если мы знаем, в каком состоянии (положении) находится выключатель в момент времени t0, и если мы прикладываем к нему воздействие, то мы всегда можем определить будущее состояние элемента.

Состояние системы x(t)

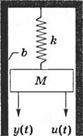
Понятие о переменных состояния, описывающих динами­ческую систему, можно проиллюстрировать на примере меха­нической системы «масса-пружина» с затуханием, изображен­ной на рис. 3.3. Число переменных состояния, выбираемых для описания системы, должно быть по возможности минималь­ным, чтобы среди них не было излишних. Для данной системы вполне достаточно иметь две переменные состояния — поло­жение и скорость движения массы. Таким образом, мы примем В качестве переменных СОСТОЯНИЯ совокупность (Х[, х2), где

Трение о стенки

Рис. 3.3. Система «масса-пружина» с затуханием

Дифференциальное уравнение, описывающее поведение системы, обычно записывается в виде

+ b^- + ky = u(t dt2 dt

С учетом введенных выше переменных состояния это уравнение примет вид:

Следовательно, исходное дифференциальное уравнение второго порядка мы можем пред­ставить в виде эквивалентной системы двух дифференциальных уравнений первого поряд­ка:

Эти уравнения по сути описывают поведение системы в терминах скорости изменения каждой переменной состояния.

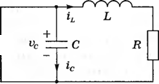
Другим примером системы, которую можно описать переменными состояния, яв­ляется ТЛС-цепь, изображенная на рис. 3.4.

Состояние системы характеризуется двумя переменными (Х[, х2) где хх есть напряжение на конденсаторе vc(/), и х2 — ток через ин­дуктивность //(/). Выбор этих переменных интуитивно понятен, т. к. общая энергия, за­пасенная в цепи, непосредственно зависит от них, как

Таким образом, Х](/0) и x2(t0) несут информацию о полной начальной энергии в цепи и, сле­довательно, о состоянии системы в момент t = /0. Для описания пассивной ЛіС-цепи число необходимых переменных состояния равно числу независимых элементов, накапливаю­щих энергию. Используя закон Кирхгофа для токов, запишем дифференциальное уравне­ние первого порядка, определяющее скорость изменения напряжения на конденсаторе:

Закон Кирхгофа для напряжений, примененный к правому контуру, дает уравнение, опре­деляющее скорость изменения тока через индуктивность:

Выход системы определяется линейным алгебраическим уравнением:

Уравнения (3.6) и (3.7) мы можем переписать в виде системы двух дифференциальных уравнений относительно переменных состояния хх и х2:

Тогда выходной сигнал будет равен

^i(0 = v0(0 = R х2. (3.10)

Используя уравнения (3.8) и (3.9), а также начальные условия [x,(f0), х2(/0)], мы сможем определить будущее поведение системы и ее выходную переменную.

Переменные состояния, описывающие систему, не являются единственными, и все­гда можно выбрать альтернативную комбинацию таких переменных. Например, для сис­темы второго порядка, такой как масса-пружина или RLC-цепь, в качестве переменных состояния можно выбрать любые две линейно независимые комбинации xx<t) и x2(t). Так, для RLC-цепи мы могли бы принять за переменные состояния два напряжения, vc(/) и v; (/), где vL — напряжение на индуктивности. Тогда новые переменные состояния, х, их'2, будут связаны со старыми переменными хх и х2 соотношениями:

х* = Vj =vc — RiL =х, — Rx2. (3.12)

Уравнение (3.12) связывает напряжение на индуктивности со старыми переменными состояния vc и iL. В реальной системе всегда можно образовать несколько комбинаций пе­ременных состояния, которые определяют энергию, запасенную в системе, и, следовате­льно, адекватно описывают ее динамику. На практике в качестве переменных состояния часто выбирают такие физические переменные, которые легко могут быть измерены.

Альтернативный метод получения модели в переменных состояния основан на испо­льзовании графа связей. Такие графы могут быть построены для электрических, механи­ческих, гидравлических и тепловых элементов или систем, а также для комбинаций эле­ментов различных типов. Графы связей позволяют получить систему уравнений относи­

тельно переменных состояния.

Переменные состояния характеризуют динамику системы. Инженера в первую оче­редь интересуют физические системы, в которых переменными являются напряжения, токи, скорости, перемещения, давления, температуры и другие аналогичные физические величины. Однако понятие состояния применимо к анализу не только физических, но так­же биологических, социальных и экономических систем. Для этих систем понятие состоя­ния не ограничивается рамками представлений об энергии и подходит к переменным со­стояния в более широком смысле, трактуя их как переменные любой природы, описываю­щие будущее поведение системы.

🌟 Видео

Метод пространства состояний САУ: описание конкретной системыСкачать

Волновая функция (видео 5) | Квантовая физика | ФизикаСкачать

Дифференциальное уравнение Эйлера. Основное уравнение гидростатикиСкачать

Лекция 1 | Динамические системы | Сергей Пилюгин | ЛекториумСкачать

c15 1, Пространство состояний: представлениеСкачать

Термодинамические системы, параметры. Равновесное, неравновесное состояния терм. систем. 10 класс.Скачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Равновесные флуктуации динамической системыСкачать

Нелинейные динамические системы, хаос и численные методы (сокращённый вариант)Скачать

Приходько А.А. «Динамические системы. Комбинаторика. Информация. Сложность» лекция 2Скачать

Динамические системы и бифуркации // Виктор КлепцынСкачать

Знакомство с теорией динамических системСкачать

Кислов А.В.- Климатология с основами метеорологии - Динамические системыСкачать

Уравнения состояния вещества — Игорь ЛомоносовСкачать