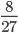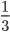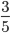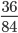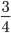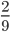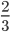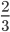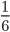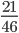Уравнение сокращение дробей 6 класс

О чем эта статья:

Видео:Основное свойство дроби. Сокращение дробей. 5 класс.Скачать

Что такое «сокращение дробей»

Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.

Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.

В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.

С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:

=

=

где a, b, m — натуральные числа.

Графически сокращение дробей обычно записывается вот так:

Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.

Больше наглядных примеров и понятных объяснений — на курсах обучения математике в онлайн-школе Skysmart.

Пример 1. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 3.

= =

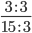
Сокращение выполнено: =

Пример 2. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 2.

= =

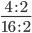
Сокращение выполнено: =

Видео:6 класс, 9 урок, Сокращение дробейСкачать

Приведение дробей к несократимому виду

Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.

Так, в результате сокращения в примере 2, мы из дроби получили дробь

Выходит, что дробь выдержит еще одно сокращение и придет к виду

Сокращая дробь, стремитесь в итоге получить несократимую дробь.

Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.

— несократимая дробь, так как по свойствам НОД мы знаем, что:

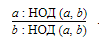
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.

• Несократимые дроби: ; ; ;

Пример 3. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 12

Найдем частное: 12 : 12 = 1

= =

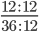
Сокращение выполнено: =

Пример 4. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 5

Найдем частное: 15 : 5 = 3

= =

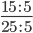
Сокращение выполнено: =

Видео:Сокращение дробей. 6 классСкачать

Правило сокращения дробей

Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.

Выполняйте сокращение дробей по следующему алгоритму:

1. Найдите НОД числителя и знаменателя дроби.
2. Разделите числитель и знаменатель дроби на НОД.

В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.

Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.

• Например, дана дробь

Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.

Пример 5. Сократите дробь

Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5

Мысленно убираем все общие множители и перемножаем оставшиеся.

= =

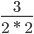
Сокращение выполнено: =

Пример 6. Сократите обыкновенную дробь

Найдем НОД числителя и знаменателя. НОД = 9

= =

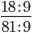
Сокращение выполнено: =

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.

Пример 6. Сократите дробь:

= = =

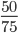
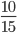
Сокращение выполнено: =

Пример 7. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

168 = 2 * 2 * 2 * 3 * 7

240 = 2 * 2 * 2 * 2 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24

НОД 168 и 240 равен 24

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

= =

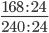
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

360 = 2 * 2 * 2 * 3 * 3 * 5

540 = 2 * 2 * 3 * 3 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180

НОД 360 и 540 равен 180

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

= =

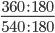
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

420 = 2 * 2 * 3 * 5 * 7

2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420

НОД 420 и 2520 равен 420

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

= =

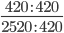
Сокращение выполнено. Дробь приведена к несократимому виду: =

Пример 9. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

1575 = 3 * 3 * 5 * 5 * 7

3450 = 2 * 3 * 5 * 5 * 23

Перемножаем все общие множители между собой 3 * 5 * 5 = 75

НОД 1575 и 3450 равен 72

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

= =

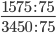
Сокращение выполнено. Дробь приведена к несократимому виду: =

Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.

Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.

Видео:Основное свойство дроби. Сокращение дробей. Математика 6 класс.Скачать

Тема дроби 6 класс, правильные, неправильные, смешанные. Примеры решения дроби 6 класс. Действия с дробями 6 класс, деление, умножение, сокращение

С дробями ученики знакомятся еще в 5 классе. Раньше людей, которые умели производить действия с дробями, считали очень умными. Первой дробью была 1/2, то есть половина, дальше появились 1/3 и т.д. Несколько веков примеры считались слишком сложными. Сейчас же разработаны подробные правила по преобразованию дробей, сложению, умножению и другим действиям. Достаточно немного разобраться в материале, и решение будет даваться легко.

Видео:Сокращение дробей - это похудение дробей))) 6 класс. Для тех, кто не понимаетСкачать

Повторение обычные дроби 6 класс

Обыкновенная дробь, которую называют простой дробью, записывается как деление двух чисел: m и n.

m — это делимое, то есть числитель дроби, а делитель n называют знаменателем.

Выделяют правильные дроби (m n).

Правильная дробь меньше единицы (к примеру 5/6 — это значит, что от единицы взято 5 частей; 2/8 — от единицы взято 2 части). Неправильная дробь равна или больше 1 (8/7 — единицей будет 7/7 и плюсом взята еще одна часть).

Так, единица, это когда числитель и знаменатель совпали (3/3, 12/12, 100/100 и другие).

Видео:Способы сокращения дробей. Сократимая и несократимая дроби. Математика 6 классСкачать

Действия с обыкновенными дробями 6 класс

С простыми дробями можно производить следующие действия:

• Расширять дробь. Если умножить верхнюю и нижнюю часть дроби на какое-либо одинаковое число (только не на ноль), то значение дроби не поменяется (3/5 = 6/10 (просто умножили на 2).
• Сокращение дробей — схоже расширению, но тут делят на какое-либо число.
• Сравнивать. Если у двух дробей числители одинаковыми, то большей окажется дробь с меньшим знаменателем. Если одинаковые знаменатели, то больше будет дробь с наибольшим числителем.
• Выполнять сложение и вычитание. При одинаковых знаменателях это сделать просто (суммируем верхние части, а нижняя не меняется). При разных придется найти общий знаменатель и дополнительные множители.
• Умножить и разделить дроби.

Примеры действий с дробями рассмотрим ниже.

Видео:Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Сокращенные дроби 6 класс

Сократить — значит поделить верхнюю и нижнюю часть дроби на какое-либо одинаковое число.

На рисунке представлены просты примеры сокращения. В первом варианте можно сразу догадаться, что числитель и знаменатель делятся на 2.

На заметку! Если число четное, то оно по-любому делится на 2. Четные числа — это 2, 4, 6…328 (заканчивается на четное) и т. д.

Во втором случае при делении 6 на 18 сразу видно, что числа делятся на 2. Разделив, получаем 3/9. Эта дробь делится еще на 3. Тогда в ответе получается 1/3. Если перемножить оба делителя: 2 на 3, то выйдет 6. Получается, что дробь была разделена на шестерку. Такое постепенное деление называется последовательным сокращением дроби на общие делители.

Кто-то сразу поделит на 6, кому-то понадобится деление частями. Главное, чтобы в конце осталась дробь, которую уже никак не сократить.

Отметим, что если число состоит из цифр, при сложении которых получится число, делящееся на 3, то и первоначальное также можно сократить на 3. Пример: число 341. Складываем цифры: 3 + 4 + 1 = 8 (8 на 3 не делится, значит, число 341 нельзя сократить на 3 без остатка). Другой пример: 264. Складываем: 2 + 6 + 4 = 12 (делится на 3). Получаем: 264 : 3 = 88. Это упростит сокращение больших чисел.

Помимо метода последовательного сокращения дроби на общие делители есть и другие способы.

НОД — это самый большой делитель для числа. Найдя НОД для знаменателя и числителя, можно сразу сократить дробь на нужное число. Поиск осуществляется путем постепенного деления каждого числа. Далее смотрят, какие делители совпадают, если их несколько (как на картинке ниже), то нужно перемножить.

Видео:МАТЕМАТИКА 6 класс: Сокращение дробей | ВидеоурокСкачать

Смешанные дроби 6 класс

Все неправильные дроби можно превратить в смешанные, выделив в них целую часть. Целое число пишется слева.

Часто приходится из неправильной дроби делать смешанное число. Процесс преобразования на примере ниже: 22/4 = 22 делим на 4, получаем 5 целых (5 * 4 = 20). 22 — 20 = 2. Получаем 5 целых и 2/4 (знаменатель не меняется). Поскольку дробь можно сократить, то делим верхнюю и нижнюю часть на 2.

Смешанное число легко превратить в неправильную дробь (это необходимо при делении и умножении дробей). Для этого: целое число умножим на нижнюю часть дроби и прибавим к этому числитель. Готово. Знаменатель не меняется.

Видео:Сокращение дробей | Математика 6 класс #9 | ИнфоурокСкачать

Вычисления с дробями 6 класс

Смешанные числа можно складывать. Если знаменатели одинаковые, то сделать это просто: складываем целые части и числители, знаменатель остается на месте.

При сложении чисел с разными знаменателями процесс сложнее. Сначала приводим числа к одному самому маленькому знаменателю (НОЗ).

В примере ниже для чисел 9 и 6 знаменателем будет 18. После этого нужны дополнительные множители. Чтобы их найти, следует 18 разделить на 9, так находится дополнительное число — 2. Его умножаем на числитель 4 получилась дробь 8/18). То же самое делают и со второй дробью. Преобразованные дроби уже складываем (целые числа и числители отдельно, знаменатель не меняем). В примере ответ пришлось преобразовать в правильную дробь (изначально числитель оказался больше знаменателя).

Обратите внимание, что при разности дробей алгоритм действий такой же.

При умножении дробей важно поместить обе под одну черту. Если число смешанное, то превращаем его в простую дробь. Далее умножаем верхнюю и нижнюю части и записываем ответ. Если видно, что дроби можно сократить, то сокращаем сразу.

В указанном примере сокращать ничего не пришлось, просто записали ответ и выделили целую часть.

В этом примере пришлось сократить числа под одной чертой. Хотя сокращать можно и готовый ответ.

При делении алгоритм почти такой же. Сначала превращаем смешанную дробь в неправильную, затем записываем числа под одной чертой, заменив деление умножением. Не забываем верхнюю и нижнюю часть второй дроби поменять местами (это правило деления дробей).

При необходимости сокращаем числа (в примере ниже сократили на пятерку и двойку). Неправильную дробь преобразуем, выделив целую часть.

Видео:Сократить дробь. Пример 08.Скачать

Основные задачи на дроби 6 класс

На видео показано еще несколько задач. Для наглядности использованы графические изображения решений, которые помогут наглядно представить дроби.

Видео:Как сокращать дроби просто. Математика 6 классСкачать

Примеры умножения дроби 6 класс с пояснениями

Перемножающиеся дроби записываются под одной линией. После этого их сокращают путем деления на одни и те же числа (например, 15 в знаменателе и 5 в числителе можно разделить на пятерку).

Видео:СОКРАЩЕНИЕ ДРОБЕЙ 5 и 6 класс математикаСкачать

Сравнение дробей 6 класс

Чтобы сравнить дроби, нужно запомнить два простых правила.

Правило 1. Если знаменатели разные

Правило 2. Когда знаменатели одинаковые

Например, сравним дроби 7/12 и 2/3.

1. Смотрим на знаменатели, они не совпадают. Значит нужно найти общий.
2. Для дробей общим знаменателем будет 12.
3. Делим 12 сначала на нижнюю часть первой дроби: 12 : 12 = 1 (это доп. множитель для 1-й дроби).
4. Теперь 12 делим на 3, получаем 4 — доп. множитель 2-й дроби.
5. Умножаем полученные цифры на числители, чтобы преобразовать дроби: 1 х 7 = 7 (первая дробь: 7/12); 4 х 2 = 8 (вторая дробь: 8/12).
6. Теперь можем сравнивать: 7/12 и 8/12. Получилось: 7/12 Примеры с дробями 6 класс для тренировки

В качестве тренировки можно выполнить следующие задания.

Видео:как решать дробиСкачать

Сложение дробей 6 класс с разными знаменателями

Видео:Сокращение дробейСкачать

Совет: если сложно найти наименьший общий знаменатель у дробей (особенно, если значения их небольшие), то можно перемножить знаменатель первой и второй дроби. Пример: 2/8 и 5/9. Найти их знаменатель просто: 8 умножаем на 9, получится 72.

Видео:СОКРАЩЕНИЕ ДРОБЕЙ. Видеоурок | МАТЕМАТИКА 6 классСкачать

Решение уравнений с дробями 6 класс

В решении уравнений требуется вспомнить действия с дробями: умножение, деление, вычитание и сложение. Если неизвестен один из множителей, то произведение (итог) делится на известный множитель, то есть дроби перемножаются (вторая переворачивается).

Если неизвестно делимое, то знаменатель умножается на делитель, а для поиска делителя нужно делимое разделить на частное.

Представим простые примеры решения уравнений:

Здесь требуется лишь произвести разность дробей, не приводя к общему знаменателю.

На видео представлено решение более сложных уравнений.

Видео:Ошибки при сокращении дробей.Скачать

Многоэтажные дроби 6 класс примеры с пояснениями

Многоэтажной дробью называют дробь, записанную в несколько строк. Пример решения многоэтажной дроби:

Как решали пример способом 1:

1. Убрали двухэтажную дробь, чтобы пример выглядел проще. Деление записали в виде двоеточия.
2. Деление на 1/2 заменили умножением на 2 (перевернули дробь).
3. Складывая 1/2 и 3/4, пришли к общему знаменателю 4. При этом для первой дроби понадобился дополнительный множитель 2, из 1/2 вышло 2/4.
4. Сложили 2/4 и 3/4 — получили 5/4.
5. Не забыли про умножение 5/4 на 2. Путем сокращения 2 и 4 получили 5/2 или 2 целых и 1/2

Ответ получился в виде неправильной дроби. Ее можно преобразовать в 2 целых и 1/2.

Во втором способе числитель и знаменатель умножили на 4, чтобы сократить нижнюю часть, а не переворачивать знаменатель.

Об Авторе

Смотрите также

Видео:Основное свойство дроби. Сокращение дробей. Практическая часть - решение задачи. 5 класс.Скачать

Красивый подарок маме своими руками, 8 марта короткие пожелания, открытка 8 марта своими руками для детей: открытки на 8 марта своими руками шаблоны, цветные шаблоны открыток

Видео:Математика 6 класс. Сокращение дробей.Скачать

Явления живой и неживой природы 2 класс: биология живая неживая природа, признаки живой и неживой природы

Видео:Сокращение дробей за 60 секундСкачать

Подарок маме на 8 марта своими руками, какую сделать поделку для мамы: в детском саду, в школе, лучшие поделки своими руками. Рисунок маме 8 марта: рисование простые рисунки

4 комментария

Отличная статья, ставлю пятерку.
Имея высшее техническое образование и помогая внучке в шестом классе я с удовольствием узнал, что внучка и без меня хорошо в дробях разбирается, а я уже и подзабыл НОК. Спасибо.

Спасибо за оценку!

Как у вас в последнем примере из 5/2 получилось 1 целая 3/5? Будет же 2 целых 1/2

большое спасибо, примите наши извинения за досадную ошибку

Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Алгебраические дроби. Сокращение алгебраических дробей в более сложных случаях

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы вспомним понятие алгебраической дроби и основы работы с ней. Мы приступим к решению более сложных примеров, в которых не всегда нужно применять очевидные формулы, а иногда стоит задуматься и приступить к разложению совсем с другой стороны.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»
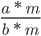
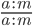
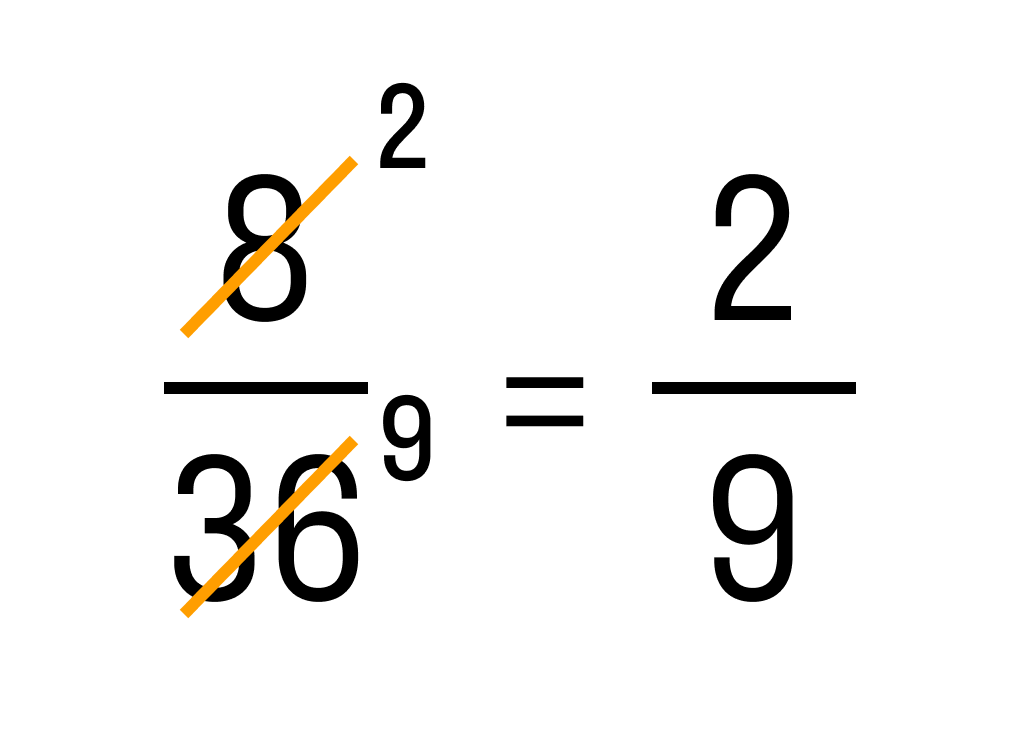
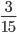
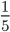
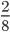
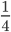
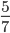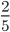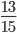