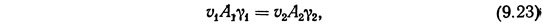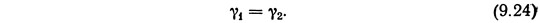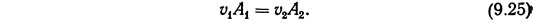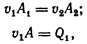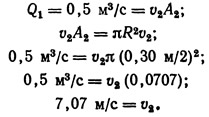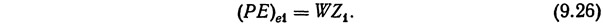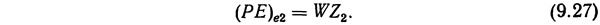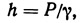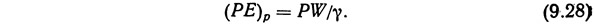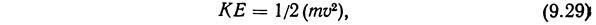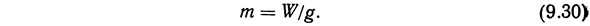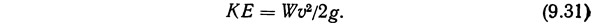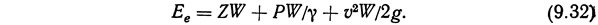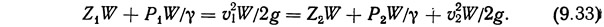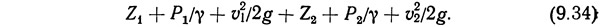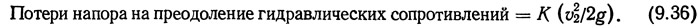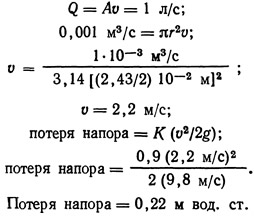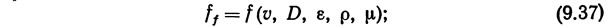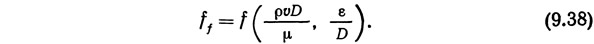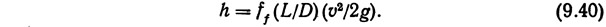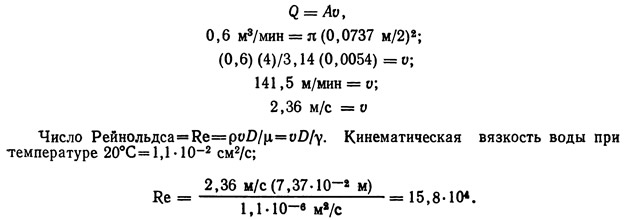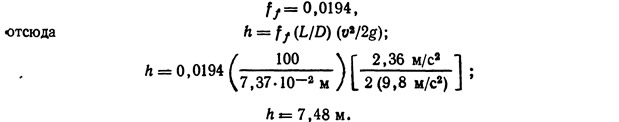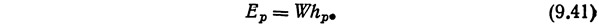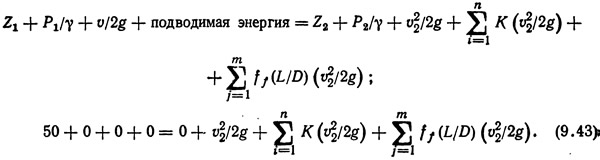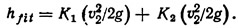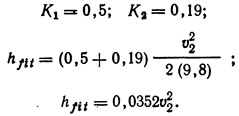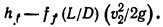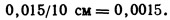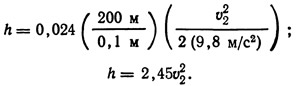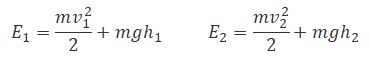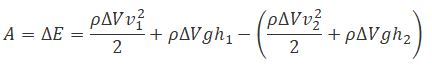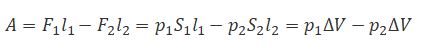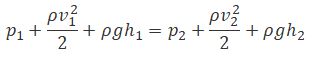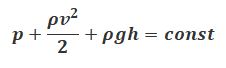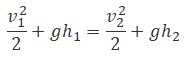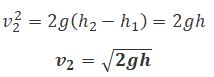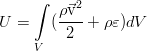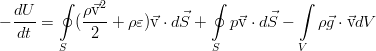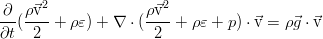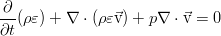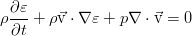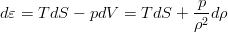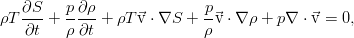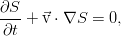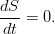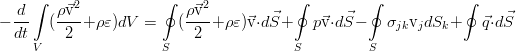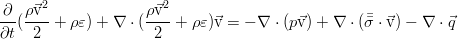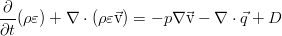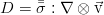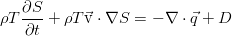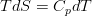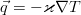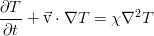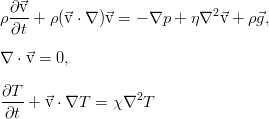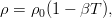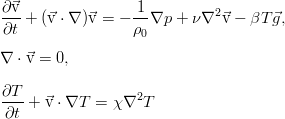Уравнение сохранения энергии в гидродинамике (2 видео)

Теория гидродинамики жидкостей

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости. Поскольку специалисты по разведению водных организмов имеют дело с движущейся водой, вопросы гидродинамики имеют для них первостепенное значение. В основе теории движения жидкостей лежат четыре физических закона: режим движения; закон сохранения масс; закон сохранения энергии и три закона движения Ньютона.

Содержание

Режим движения
Закон сохранения масс
Закон сохранения энергии
Уравнение сохранения энергии в гидродинамике
Кратко о гидродинамике: сохранение энергии
Перенос энергии в идеальной жидкости
Учёт вязкости. Уравнение теплопроводности
Конвекция. Приближение Буссинеска
Проблема инструментария
Далее
🎦 Видео

Видео:Закон БернуллиСкачать

Режим движения

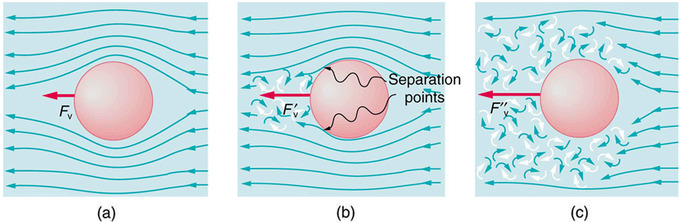
Режим движения жидкостей может быть ламинарным и турбулентным. Если представить жидкость как тело, состоящее из отдельных частиц или элементов, то ламинарный режим движения можно определить как движение, при котором все частицы тела движутся в одном направлении с одинаковой скоростью. Таким образом, частицы образуют струйки (или слои), движение которых относительно друг друга постоянно и завихрения отсутствуют.

Турбулентное движение характеризуется поперечным перемещением струй, завихрениями и другими хаотичными движениями. Потери энергии в турбулентном потоке больше, чем в ламинарном, из-за значительного внутреннего трения.) Для ламинарных потоков благоприятны низкие скорости потоков, трубопроводы небольшого диаметра и высокие вязкости жидкости. Для турбулентного режима благоприятны) противоположные условия. На предприятиях по разведению водных организмов, как правило, имеют дело с турбулентными потоками, так как при высоких ско-ростях1 движения жидкости стоимость эксплуатации трубопроводов уменьшается.

Видео:7.1.6 Уравнение энергии в гидродинамике. Потоки теплоты и работы. Уравнение состояния веществаСкачать

Закон сохранения масс

В замкнутом трубопроводе количество жидкости, протекающее через все его сечения, постоянно. На рис. 9.8 изображен участок замкнутого трубопровода, по длине которого взято два сечения — 1 и 2.

Поскольку через оба сечения должно пройти одинаковое количество воды, для этой системы на основе закона сохранения масс можно записать следующее уравнение:

где v — скорость; А — площадь поперечного сечения; γ — удельный вес жидкости.

Учитывая несжимаемость жидкости, проходящей через сечения 1 и 2, можно принять, что

Тогда уравнение (9.23) принимает вид

Уравнение (9.25) называется уравнением неразрывности и является одним из основных уравнений гидродинамики. Полученное Для движения несжимаемой жидкости по замкнутому трубопроводу уравнение (9.25) распространяется также, на движение несжимаемой жидкости в открытом канале.

Пример 9.4. Определить скорость потока в сечении 2 (см. рис. 9.8), если в сечении 1 она составляет 0,5 м/с, а диаметр трубопровода в сечении 2 равен 30 см.

где Q₁ — объем жидкости, протекающей в единицу времени через сечение 1.

Видео:Урок 122. Закон сохранения полной механической энергииСкачать

Закон сохранения энергии

Из закона сохранения энергии вытекает еще одно уравнение гидродинамики, позволяющее решать различные задачи. Энергия, которой обладает частица жидкости в любой точке, состоит из потенциальной энергии положения, потенциальной энергии давления и кинетической энергии движения.

Частица жидкости в сечении 1 (см. рис. 9.8) обладает потенциальной энергией, обусловленной ее положением относительно плоскости сравнения или плоскости нулевого энергетического потенциала. Эту энергию (РЕ) е можно выразить как произведение веса частицы W на ее геометрическую высоту над плоскостью сравнения Z₁:

Аналогично для частицы в сечение 2 (см. рис. 9.8) можно записать

Если жидкость находится под давлением, она обладает потенциальной энергией давления. На рис. 9.9 показан резервуар, заполненный жидкостью, нижняя часть которого переходит в горизонтальный трубопровод. На конце трубопровода установлен клапан, предотвращающий свободное вытекание жидкости из резервуара. Потенциальная энергия частицы в точке 1 (см. рис. 9.9) определяется только ее геометрической высотой, так как единственное давление, оказываемое на поверхность жидкости в! этой точке,— это атмосферное давление, величина которого совпадает с нулевым значением на манометрической шкале отсчета. При закрытом клапане на трубопроводе давление в точке 2 согласно уравнению (9.7) будет равно γh (h — высота заполнения резервуара жидкостью). Это давление способно производить работу, поэтому его можно рассматривать как одну из форм потенциальной энергии. Энергия давления (РЕ)_р может быть выражена как произведение веса элементарной частицы жидкости на приложенное к ней давление. В соответствии с уравнением (9.7) давление жидкости можно определить по формуле

Движущиеся жидкости обладают кинетической энергией, которую можно определить из основного уравнения

где m — масса; v — скорость.

В соответствии с законами Ньютона

Подставляя формулу (9.30) в уравнение (9.29), получим

Уравнение (9.31) характеризует кинетическую энергию частицы жидкости, движущейся со скоростью V.

Полная энергия частицы жидкости Е_е является сумммой потенциальной и кинетической энергии. На основании уравнений (9.26). (9.28) и (9.31) можно получить следующее математическое выражение для величины полной энергии:

В соответствии с законом сохранения энергии полная энергия частицы жидкости в точке 1 должна быть равна полной энергии частицы жидкости в точке 2 (см. рис. 9.9):

Разделив левую и правую части последнего уравнения на W, получим

Уравнение (9.34), известное как уравнение Бернулли, применимо к идеальной жидкости, не имеющей энергетических потерь на участке между сечениями 1 и 2.

В реальных жидкостях всегда имеются потери на трение жидкости о стенки трубопроводов. С учетом этих потерь уравнение Бернулли должно быть переписано следующим образом:

Из уравнения (9.35) видно, что подводимая энергия (например, от насоса, расположенного между точками 1 и 2) должна входить в левую часть уравнения как положительная величина. Потери, обусловленные гидравлическими сопротивлениями, и потери на трение жидкости о стенки трубопровода должны фигурировать в правой части уравнения, относящейся к частице жидкости, расположенной в нижнем по направлению движения жидкости сечении трубопровода, так как они выражают энергетические потери на преодоление сопротивлений трения при движении жидкости от точки 1 до точки 2.

Потери, связанные с преодолением местных гидравлических сопротивлений, возникают при изменении размера поперечного сечения в направлении потока, входе и выходе жидкости и вследствие других изменений Величина таких потерь определяется экспериментально и учитывается при расчетах коэффициентом потерь K, умноженным на скоростной напор:

Полученные экспериментально коэффициенты потерь для трубопроводов приведены в табл. 9.2.

Если на рассматриваемом участке между двумя сечениями трубопровода системы имеется два или более гидравлических сопротивления, потери на их преодоление суммируются.

Пример 9.5. Определить потерю напора в колене трубопровода, изогнутого под углом 90°, с номинальным диаметром, равным 2,54 см, если расход жидкости через это колено составляет 60 л/мин.

Внутренний диаметр трубы с номинальным диаметром 2,54 см равен 2,43 см.

Потери на трение, обусловленные трением жидкости о стенки трубопровода, зависят от скорости движения жидкости, ее плотности, вязкости, диаметра трубопровода и характера шероховатости его стенок. Математически это выражается следующим образом:

где f₁ — коэффициент сопротивления трения; v — скорость потока; D — диаметр трубопровода; ε — шероховатость стенок трубопровода (абсолютная); ρ — плотность жидкости; μ — вязкость жидкости; f — функция.

Пять членов этой формулы можно представить в виде двух безразмерных величин:

Одна из этих безразмерных величин ρυD/μ известна как число Рейнольдса (которое может быть выражено так же как υD/v, где v — кинематическая вязкость); другая называется относительной шероховатостью. Можно рассматривать число Рейнольдса как отношение сил инерции к силам вязкости. Число Рейнольдса определяет режим движения потока (ламинарный или турбулентный). Если Re>2000, режим ламинарный, при Re>4000 режим становится турбулентным. В диапазоне чисел Рейнольдса от 2000 до 4000 режим движения потока нестабильный (неустановившееся течение). Потоки, характеризующиеся числами Рейнольдса в этом диапазоне, считаются неблагоприятными в инженерной практике и их следует по возможности избегать.

Вторая безразмерная величина в уравнении (9.37) — ε/D — это относительная шероховатость. Она представляет собой отношение высоты выступов шероховатости на внутренней поверхности трубы к диаметру трубы. Коэффициент сопротивления трения f_f также является безразмерной величиной.

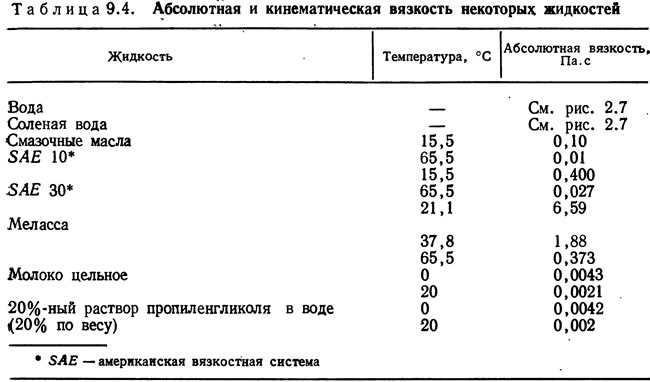
Экспериментальные работы Муди по определению значений безразмерных членов уравнения (9.38) позволили представить зависимость между этими величинами в виде диаграммы, известной теперь как диаграмма Муди (рис. 9.10). По горизонтальной оси диаграммы Муди отложены числа Рейнольдса, по вертикальной — коэффициент сопротивления трения, значения относительной шероховатости представлены отдельной кривой. В ламинарном режиме (Re 4000 имеет место турбулентное движение, в этом режиме зависимость между числом Рейнольдса и коэффициентом сопротивления трения носит нелинейный характер. Коэффициент шероховатости зависит от материала стенки (табл. 9.3). Для определения числа Рейнольдса можно воспользоваться данными, приведенными в табл. 9.4.

Определив коэффициент сопротивления трения, можно подсчитать потерю напора на преодоление местных сопротивлений:

где h — потеря напора, связанная с местными сопротивлениями, м; f_f — коэффициент сопротивления трения (безразмерная величина); L — длина трубопровода, м; D — диаметр трубопровода, м; v — скорость потока, м/с; g — ускорение силы тяжести, м/с 2 .

Пример 9.6. Определить потерю напора в оцинкованном трубопроводе длиной 100 м с номинальным диаметром 7,62 см, по которому перепускается вода температурой 20 °С. Расход воды составляет 0,06 м/мин.

Внутренний диаметр трубы с номинальным диаметром 7,62 см равен 7,37 см по американским стандартам на трубопроводы.

Абсолютная шероховатость оцинкованной трубы по табл. 9.3. равна 0,015 см. Отношение абсолютной шероховатости к диаметру трубы дает относительную шероховатость, в этом примере она равна 0,002. По диаграмме Муди коэффициент сопротивления трения

Подводимая энергия на участке трубы между двумя сечениями 1 и 2 [уравнение (9.35)] — это энергия, обычно обеспечиваемая насосом. Необходимо уточнить и конкретизировать эту величину, чтобы получить для нее математическое выражение. Сообщаемую насосом энергию Е_р можно представить как произведение веса жидкости W на полный напор системы h_p, который должен преодолевать этот насос [уравнение (9.38)];

Вводя это выражение в левую часть уравнения (9.33) вместо величина напора hp, создаваемая насосом, и будет характеризовать величину подводимой энергии в уравнении (9.35).

Теперь уравнение (9.35) можно записать с учетом формул (9.36), (9.40) и (9.41):

Пример 9.7. Определить расход через оцинкованный трубопровод (рис. 9.11) диаметром 10 см и длиной 200 м; h₁=20 м, h₂=30 м. В начале трубы расположена полностью открытая задвижка. Число Рейнольдса для трубы равно 1·10 5 .

Для двух сечений, взятых по длине трубопровода 1 и 2, может быть записано уравнение Бернулли. Выбор этих сечений обусловлен соображениями удобства: скорость течения жидкости в сечении 1 может быть принята равной нулю, если учесть, что вместимость резервуара достаточно велика, чтобы движением жидкости в этом сечении 1 можно было пренебречь. Поскольку оба сечения 1 и 2 соединены с атмосферой, манометрическое давление, оказываемое на жидкость в этих сечениях, равно нулю. Уравнение Бернулли будет иметь вид

Отдельно для каждого гидравлического сопротивления необходимо определить потерю напора: h_fit = потеря напора на входе (кромка прямоугольной формы) + потеря напора в задвижке;

Из табл. 9.2 берут значения:

Потеря напора, вызванная трением жидкости о стенки трубы,

Коэффициент сопротивления трения берется по диаграмме Муди.

Число Рейнольдса задано, оно равно 1·10 5 .

Относительная шероховатость оцинкованной трубы составит

От точки 1·10 5 на горизонтальной оси диаграммы Муди следует восстановить перпендикуляр до пересечения с кривой относительной шероховатости,, соответствующей значению 0,0015, и, следя по горизонтальной оси, найти значение коэффициента сопротивления трения, которое будет равно примерно 0,024.

С помощью уравнения (9.40) можно определить

Подстановка полученных значений в уравнение (9.43) дает выражение для расхода:

Видео:Урок 126. Задачи на закон сохранения энергии (ч.1)Скачать

Уравнение сохранения энергии в гидродинамике

Гидродинамика — раздел физики сплошных сред, изучающий движение идеальных и реальных жидкости и газа.

Как и в других разделах физики сплошных сред, прежде всего осуществляется переход от реальной среды, состоящей из большого числа отдельных атомов или молекул, к абстрактной сплошной среде, для которой и записываются уравнения движения.

Идеальная среда

Гидродинамика изучает поведение идеальной жидкости — воображаемой среды без вязкости, сил трения и теплопроводности. Касательные напряжения равны нулю. Её можно представить, как систему небольших упругих шаров с пренебрежимо малым объёмом, не прилипающих друг к другу. Они часто сталкиваются друг с другом. Поэтому каждый шар переносит при движении массу, импульс, момент импульса, энергию.

Ламинарное и турбулентное движения жидкости

Экспериментально установлено, что в природе существуют два различных вида движения потока — ламинарное (слоистое, упорядоченное), при котором отдельные слои жидкости скользят друг относительно друга, и турбулентное (неупорядоченное), когда частицы жидкости движутся по сложным, все время изменяющимся траекториям.

Вследствие этого затрата энергии на турбулентное движение потока больше, чем на ламинарное.

Турбулентность — название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средний значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов. Происходит их нелинейное вихревое взаимодействие и распространение в пространстве и времени.

Турбулентность может возникать и при нарушении сплошности среды, например, при кавитации (кипении). При опрокидывании и разрушении волны прибоя возникает многофазная смесь воды, воздуха, пены. Мгновенные параметры среды становятся хаотичными.

Ламинарное течение

Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости.

Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.

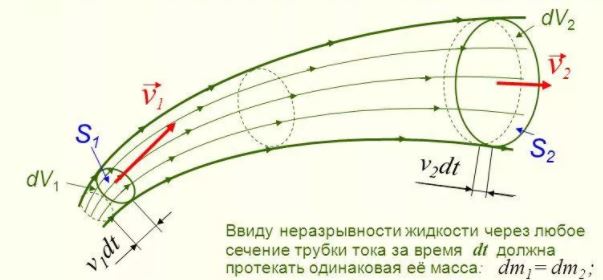
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости — потоком. Графически движение жидкостей изображается с помощью линий тока. Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, ограниченная линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока, называется элементарной струйкой.

Для случая установившегося движения элементарной струйке придаются следующие свойства:

форма элементарной струйки остается неизменной с течением времени;
через стенки элементарной струйки движение жидкости не происходит (обмена энергией жидкости между элементарными струйками нет);
вследствие малости поперечного сечения элементарной струйки скорость и гидродинамическое давление во всех точках ее поперечного сечения одинаковы.

Уравнение неразрывности жидкости

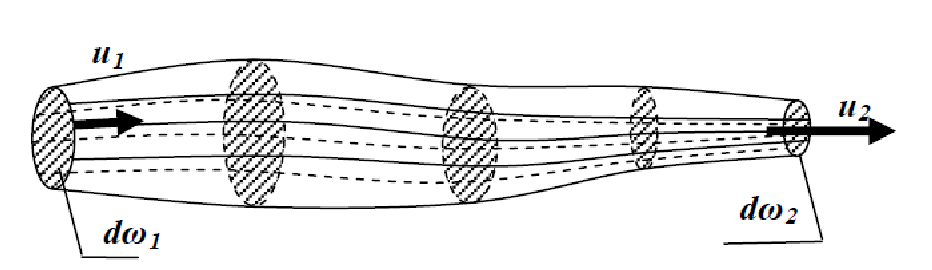
В гидравлике обычно рассматривают потоки, в которых не образуются разрывы. Если выделить в потоке два любых сечения, отстоящих друг от друга на некотором расстоянии, то за время Δ t через сечение S проходит объем жидкости SvΔ t; следовательно, за 1 с через S 1 пройдет объем жидкости S 1 v 1 , где v 1 — скорость течения жидкости в месте сечения S 1 . Через сечение S 2 за 1 с пройдет объем жидкости S 2 v 2 , где v 2 — скорость течения жидкости в месте сечения S 2 . Здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ = const), то через сечение S 2 пройдет такой же объем жидкости, как и через сечение S 1 , т. е.

Произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение называется уравнением неразрывности для несжимаемой жидкости.

Уравнение Бернулли

При движении идеальной жидкости не происходит превращения механической энергии во внутреннюю, поэтому выполняется закон сохранения механической энергии.

Стационарным принято называть такой поток жидкости, в котором не образуются вихри. В стационарном потоке частицы жидкости перемещаются по неизменным во времени траекториям, которые называются линиями тока. Опыт показывает, что стационарные потоки возникают только при достаточно малых скоростях движения жидкости.

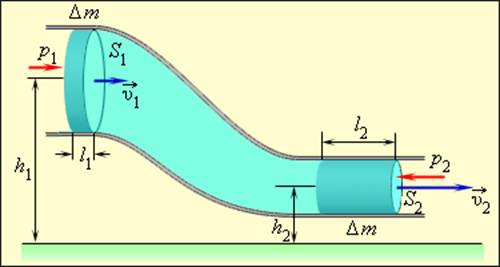
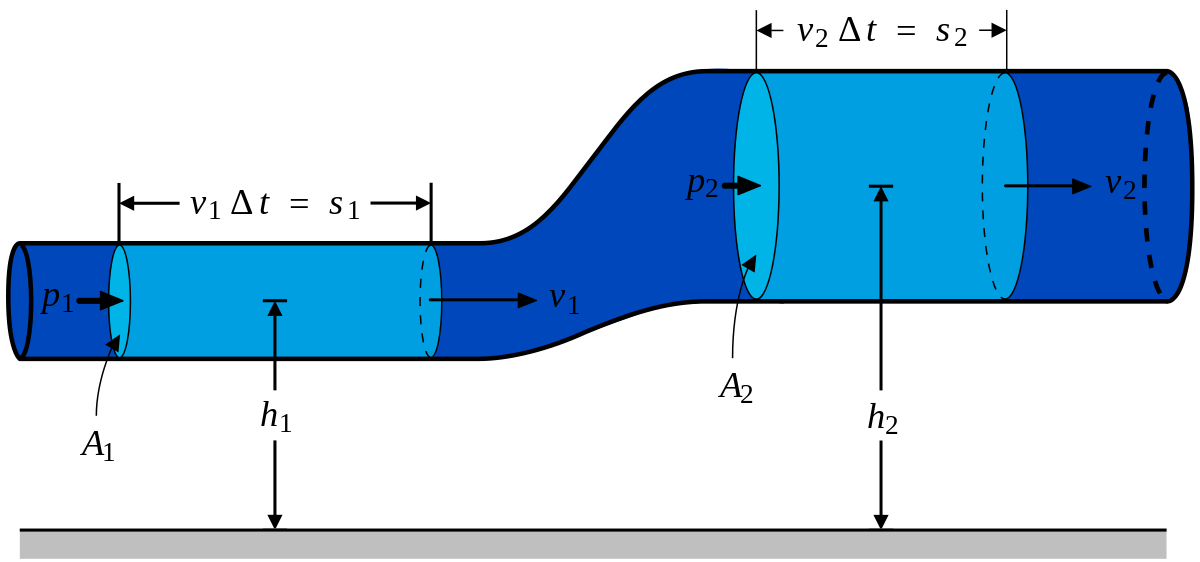
Рассмотрим стационарное движение идеальной несжимаемой жидкости по трубе переменного сечения. Различные части трубы могут находиться на разных высотах. У идеальной жидкости трение полностью отсутствует.

Выделим в стационарно текущей несжимаемой идеальной жидкости трубку тока, ограниченную сечениями S₁ и S₂, по которой жидкость течет слева направо. Пусть в месте сечения S₁ скорость течения v₁ давление р₁ и высота, на которой это сечение расположено, h₁. Аналогично, в месте сечения S₂ скорость течения v₂, давление р₂, высота сечения h₂. За малый промежуток времени Δt жидкость перемещается от сечения S₁ к сечениюS‘₁, от S₂ к S’₂.

Согласно закону сохранения энергии, изменение полной энергии Е₂ — Е₁ идеальной несжимаемой жидкости должно быть равно работе А внешних сил по перемещению массы т жидкости, где

— полные энергии жидкости массой т в местах сечений S₁ и S₂ соответственно.

С другой стороны, А — это работа, совершаемая при перемещении всей жидкости, заключенной между сечениями S₁ и S₂, за рассматриваемый малый промежуток времени Δt:

где р — статическое давление (давление жидкости на поверхность обтекаемого ею тела),

ρv 2 /2 — динамическое давление.

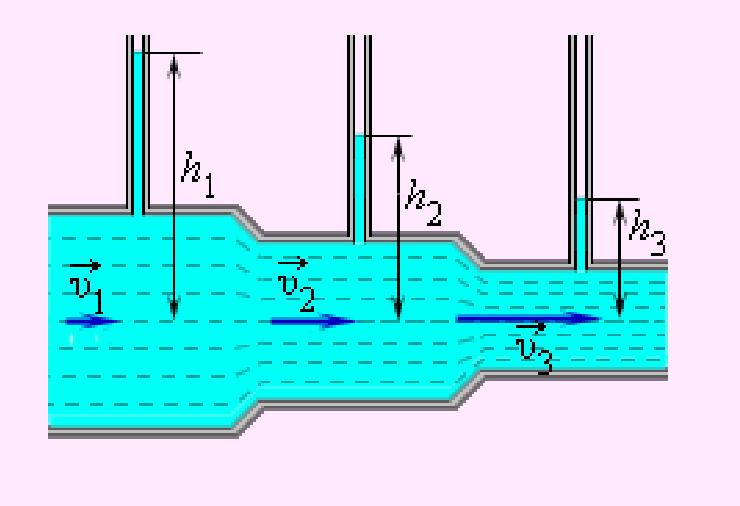
1. Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности следует, что при те чении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах, т. е. там, где скорость меньше.

Это можно продемонстрировать, установив вдоль трубы ряд манометров. В соответствии с уравнением Бернулли опыт показывает, что в манометрической трубке В, прикрепленной к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, прикрепленных к широкой части трубы.

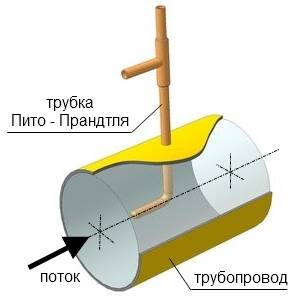
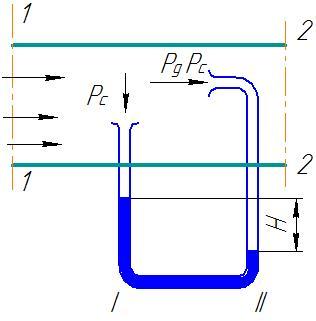
2. Так как динамическое давление связано со скоростью движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито — Прандтля. Прибор состоит из двух изогнутых под прямым углом трубок, противоположные концы которых присоединены к манометру. С помощью одной из трубок измеряется полное давление (р₀), с помощью другой — статическое (р).Манометром измеряется разность давлений:

где ρ — плотность жидкости в манометре. С другой стороны, согласно уравнению Бернулли, разность полного и статического давлений равна динамическому давлению:

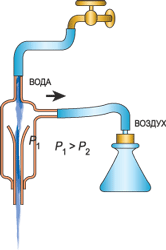
3. Уменьшение статического давления в точках, где скорость потока больше, положено в основу работы водоструйного насоса. Струя воды подается в трубку, открытую в атмосферу, так что давление на выходе из трубки равно атмосферному. В трубке имеется сужение, по которому вода течет с большей скоростью. В этом месте давление меньше атмосферного. Это давление устанавливается и в откачанном сосуде, который связан с трубкой через разрыв, имеющийся в ее узкой части. Воздух увлекается вытекающей с большой скоростью водой из узкого конца. Таким образом можно откачивать воздух из сосуда до давления 100 мм рт. ст. (1 мм рт. ст. = 133,32 Па).

4. Уравнение Бернулли используется для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, в боковой стенке которого на некоторой глубине ниже уровня жидкости имеется маленькое отверстие.

Рассмотрим два сечения (на уровне h₁ свободной поверхности жидкости в сосуде и на уровне h₂ выхода ее из отверстия). Напишем для них уравнение Бернулли:

Так как давления р₁ и р₂ в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. p₁ = p₂ , то уравнение будет иметь вид

Из уравнения неразрывности следует, что v₂/v₁ = S₁/S₂, где S₁ и S₂ — площади поперечных сечений сосуда и отверстия. Если S₁>>S₂, то членом v 2 ₁/2 можно пренебречь и

Это выражение получило название формулы Торричелли .

Видео:Закон сохранения и превращения энергии. 9 класс.Скачать

Кратко о гидродинамике: сохранение энергии

В очередной раз извиняюсь за медленное написание постов в запланированной серии. В этот раз причина промедления объективна, в виде конференции в Вене, хотя и имеет значимую субъективную составляющую в виде собственного там участия и некоторых бюрократических моментов подготовки и оплаты.

Данный пост рассматривает законы сохранения энергии в идеальной и вязкой жидкости. Они заведомо необходимы для полноты описания движения, однако, в изотермическом случае теплообмена как такового нет, и потому для описания достаточно использовать уравнение Навье-Стокса и уравнение неразрывности. Надеюсь, этот пост будет последним из достаточно абстрактных постов, описывающих общую теорию и не практически привязанных к конкретным постановкам задач.

Постараюсь уменьшить количество выкладок, ибо они, конечно, важны, но результаты в виде конечных уравнений — важнее.

Перенос энергии в идеальной жидкости

Итак, сохранение энергии. Подход к описанию абсолютно стандартный — мы вводим некоторую величину, находим, какие механизмы отвечают за её изменение и пишем закон сохранения сперва в интегральной форме, а затем, сведя все поверхностные интегралы к объёмным по теореме Гаусса — в дифференциальной.

Энергия жидкости в классической гидродинамике, не учитывающей также такой эффект, как электропроводность и соответствующее взаимодействие с внешними и внутренними электромагнитными полями, складывается из внутренней и кинетической энергии. Она равна такому интегралу:

Изменяться в пределах нашего объёма V энергия может за счёт простого её перетекания вместе с потоком жидкости, работы сил давления от внешних элементов жидкости и работы внешних сил (ниже показаны на примере силы тяжести):

В идеальной жидкости нет трения, и потому нет рассеяния энергии за счёт вязкости. Кроме того, здесь пренебрегается и процессами теплопроводности, что так же присуще идеальной жидкости как отсутствие ещё одного механизма диссипации энергии. В дифференциальной форме закон сохранения полной энергии выглядит так:

Однако, его можно благополучно упростить. Воспользовавшись уравнением Эйлера (см. предыдущий пост), скалярно домноженным на скорость, можно выделить из полученного закона сохранения такую часть:

А это уже преобразуется к ещё более простому виду:

Тут уже можно вспомнить термодинамику. Первое начало термодинамики (с пометкой — для удельного объёма жидкости, т.е. объёма, масса которого равна единице):

позволяет вполне очевидным образом связать производные энергии, энтропии и плотности (как обратной объему величины). Используя эту связь дифференциалов величин в уравнении для энергии:

а также закон сохранения массы, получим ещё одно уравнение, которое описывает эволюцию энтропии в жидкости:

В движущейся системе отсчёта, привязанной к тому элементу жидкости, для которого это всё написано, уравнение упрощается ещё сильнее:

То есть, энтропия отдельной произвольной жидкой частицы (в идеальной жидкости) сохраняется. Энтропия просто пассивно переносится потоком, попутно связывая уравнением состояния давление и плотность среды.

Учёт вязкости. Уравнение теплопроводности

Теперь учтём вязкую и теплопроводную диссипацию. В интегральном виде они представляется парой добавочных слагаемых в законе сохранения:

Они описывают работу сил вязкого трения на границе элемента жидкости и тепловой поток через границу. В дифференциальной форме уравнение сохранения полной энергии:

Произведя ряд операций над этим соотношением с применением уравнения переноса импульса в общем виде (для произвольного тензора вязких напряжений) и уравнения неразрывности (а именно — домножив закон сохранения массы на половину квадрата скорости, закон сохранения импульса — на скорость, сложив их между собой и вычтя итог из уравнения для полной энергии), мы избавимся от слагаемых с кинетической энергией:

Здесь возникает диссипативная функция, равная двойной свёртке тензора вязких напряжений и тензора, который условно иногда называют градиентом скорости:

Применив здесь уравнение баланса массы и первое начало термодинамики аналогично тому, как это сделано выше, приходим к уравнению баланса энтропии:

Видно, что оно отличается от уравнения в идеальной жидкости только ненулевой правой частью. Для несжимаемой жидкости мы можем благополучно перейти от энтропии к более осязаемой величине, то бишь — к температуре, используя определение теплоёмкости при постоянном давлении:

Наконец, можно пренебречь диссипативной функцией, т.к. она описывает выделение за счёт внутреннего трения, и потому существенна только в жидкостях с очень большими вязкостями, а для потока тепла воспользоваться законом теплопроводности Фурье, позволяющим выразить его через температуру:

В итоге получается уравнение теплопроводности несжимаемой вязкой жидкости:

Согласно ему, температура элемента жидкости изменяется за счёт непосредственного конвективного переноса с потоком жидкости, а также за счёт вполне обычного механизма молекулярной теплопроводности (правая часть).

Конвекция. Приближение Буссинеска

Собственно, с описания задачи конвекции на хабре и начался весь этот гидродинамический «балаганчик». Итак, мы смотрим на баночку с несжимаемой вязкой жидкостью, например, водой. Движение её в случае неоднородной температуры в объёме описывается тремя уравнениями:

В общем случае в эту систему входит ещё уравнение состояния, связывающее плотность, давление и температуру. Однако тогда жидкость уже нельзя считать несжимаемой. Практика же (да и математика) показывает, что с достаточной точностью можно принять плотность постоянной везде, кроме слагаемого с силой тяжести. Более того, достаточно ограничиться линейным разложением по температуре:

Сразу отметим, что здесь записана уже не абсолютная температура, а уже отклонение от некоторого «нулевого» уровня, при котором плотность равна 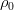. Писать так нам позволяет уравнение теплопроводности, благо оно линейное и к таким сдвигам инвариантно. Можно выделить в слагаемом при силе тяжести независимую от температуры часть (гидростатический градиент) и спрятать её в давление:

И тогда мы приходим к уравнениям конвекции в приближении Буссинеска:

Данная модель практически общеупотребительна при изучении конвективных явлений, и на её основе было получено огромное количество самых разных по значимости результатов. В частности, в задачах устойчивости равновесия жидкости и прочих.

Проблема инструментария

Немного отступлю от темы, хотя прекрасно понимаю, что это может только разжечь лишнюю и отвлекающую дискуссию.

Знаете, что удивило в комментариях по предыдущему посту? То, что читатели уделяют много внимания вопросу математической строгости выкладок, которой тут, в общем-то, немного. Гидродинамика создана Эйлером и Навье во времена господства французского материализма, когда строгие результаты аналитической механики описали, казалось, весь мир. Но уровень строгости этих результатов таков, каким он мог быть в те времена, в едва только-только созданном Ньютоном и другими дифференциальном исчислении, и не выше. И таким он остался по сей день, и такой же является математическая строгость гидродинамики. Практически, это последняя классическая область науки, которая ещё имеет нерешённые фундаментальные проблемы. Может быть, не решены они именно потому, что сформулированы на том, старом, не сильно развитом и не богатом значительными средствами языке. Помнится, есть отдельные наработки в математике, где к уравнениям Навье-Стокса применяют аппарат, не к ночи будь помянут, биспиноров и гамма-матриц Дирака (основу квантовой теории поля) или ещё чего похуже. Но они до сих пор отдельные и практически неизвестные.

Лично я предполагаю, что развитие аппарата для решения уравнений Навье-Стокса ещё попросту не состоялось. Ведь, как известно, эти уравнения отлично описывают и упорядоченные ламинарные течения, и хаос турбулентности. А в уравнениях для этого всего-то достаточно изменить один управляющий параметр. Как в нелинейных системах (а-ля система Лоренца), которые тоже не имеют общих аналитических решений, да и, в целом, конкретного детального анализа свойств решений именно как математических функций. Многое на уровне поведения — тут хаос, там упорядочение, там синхронизация, здесь влияние параметра, а переход, по-видимому, происходит вот таким образом. Но ни о гладкости решений, ни об их существовании вопроса в таких задачах нет, в отличие от Навье-Стокса. Ведь мы же до сих пор практически не знаем — существуют ли вообще их общие гладкие решения.

Увидев в комментариях вещи навроде «набла — это 1-форма», сперва сильно задумался, не упустил ли чего в своём образовании. Да, про разного рода n-формы у меня в курсах упоминалось (но не более) в одном семестровом спецкурсе под названием теории групп в физике, из которого, правда, много вынести не удалось ввиду отсутствия серьёзной структурированности изложения. Но рассуждать о том, набла — вектор или же нет, никогда не приходится. В физике, не касающейся значительно математизированных проблем уровня, скажем, общей теории относительности и неотъемлемо нужной для неё дифференциальной геометрии, набла всегда была практически вектором. Конечно, не совсем обычным, не коммутирующим с ними и обладающим рядом иных свойств. Простой, в общем-то даже обычный оператор, который показывает, какую компоненту вектора и каким образом мы будем дифференцировать. Просто инструмент, которым мы умеем пользоваться в заданных пределах и осознаём, что нужно проверить его пригодность при выходе за границу привычной области, даже, например, при переходе от декартовых координат к тем же сферическим.

Иногда можно потратить излишне много времени на понимание устройства молотка, но так толком и не научиться забивать им гвозди. Например, почему он имеет такую форму, почему разные молоты имеют разную форму, а затем начать копать глубже — почему блестит металл, а деревянная ручка — нет, и др. Но от этого понимания сущность наиболее частого применения молотка не поменяется. Им будут забивать гвозди, выравнивать металл по оправке и т.д. — им всё равно будут стучать, желательно, не по пальцам.

На таком уровне находится моё личное знакомство с аппаратом квантовой электродинамики. По принципу — помню, что-то проходил. Более того, даже методичку в прошлом году издали с преподавателем этого предмета, но как-то оно всё равно в стороне — не занимаюсь этим.

Следующий пост будет посвящён проблемам устойчивости для равновесия и стационарного течения. Там в очередной раз мы увидим, что даже простейшие задачи гидродинамики не могут быть решены аналитически в полном виде, и потому приходится применять множество различных, на первый взгляд весьма спорных, но в то же время прекрасно работающих и обоснованных методик. Надеюсь, что уже удастся перейти от абстрактности к более осязаемым вещам.