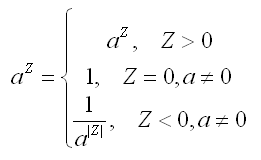Уравнение со степенями в паскале (5 видео)

Содержание

Возведение числа в степень
Задача
Решение
Уравнение со степенями в паскале
Создание программы решения уравнений второй и выше степени в системе Pascal ABC
Функция Power
Подпишись на новости, чтобы ничего не пропустить
Пример использования функции Power
Возведение в степень в Паскале
🎦 Видео

Видео:Математические выражения их запись в ПаскалеСкачать

Возведение числа в степень

Задача

Как на языке Pascal возвести число в степень.

Решение

Алгоритм решения задачи:

Чтобы возвести число в степень, его надо умножить само на себя количество раз, равное показателю степени. Т.е. возведение числа n в степень d будет выглядеть так:

n d = n₁ * n₂ * n₃ * … * n_d, где индексы внизу просто указывают очередное по счету n.

Если d равно нулю, то, какое бы число не стояло в основании степени, результат всегда будет равен единице:

Если показатель степени отрицателен (d Добавить комментарий

Видео:Уравнение четвертой степениСкачать

Уравнение со степенями в паскале

Видео:Математика это не ИсламСкачать

Создание программы решения уравнений второй и выше степени в системе Pascal ABC

Автор работы награжден дипломом победителя II степени

На сегодняшний день невозможно представить себе какую-либо область деятельности, обходящуюся без применения компьютерной техники. Компьютеры используются при проведении бухгалтерских расчетов, при решении инженерных задач, в процессе управления производством, при получении оценок производственных ситуаций и во многих других случаях. Уравнения второго и выше порядка встречаются довольно часто при изучении прикладных предметов. При решении уравнений нередко возникает необходимость разложить на множители многочлен, степень которого равна двум, трем или выше, а затем требуется проверить решение. Чтобы быстро справиться с проверкой решения таких уравнений, можно воспользоваться средствами вычислительной техники – составить программу на языке программирования Pascal ABC.

Таким образом, актуальность исследования объясняется тем, что проблемы проверки решения уравнения порядка второго и выше остро стоят перед обучающимися, а решиться такие проблемы могут через совершенствования математических знаний и составления прикладных программ. В свою очередь эти знания могут применяться на практике для решения уравнений, что улучшит проверку знаний обучающихся и значительно сократит время на их решение.

Объектом исследования является схема Горнера, и система программирования Pascal ABC.

Предметом исследования выступают алгоритм Горнера для решения уравнений второго порядка и выше в системе программирования Pascal ABC.

Цель исследования – реализация решения уравнений второго и выше порядка, основываясь на схеме Горнера в среде программирования Pascal ABC.

Цель и предмет исследования обусловили необходимость решения следующих задач:

Исследовать важность данной проблемы у обучающихся 9 – 11 классов и выявить эффективность взаимосвязи математического алгоритма и системы программирования Pascal ABC.

Определить эффективность создания программы решения уравнений.

Оценить перспективы от создания программы.

Основу гипотезы исследования составили предположения о том, что если изучить схему Горнера, то найти решение для автоматического определения корней уравнения второго и выше порядка будет проще.

В процессе исследования использовались методы системного, математического и информационного анализа. В качестве информационной базы были использованы материалы, научные труды специалистов в области программирования, и справочные материалы, концепции, представленные в современной математике.

В ходе исследования были использованы следующие группы методов:

теоретические: теоретический анализ литературы по проблеме; систематизация полученной информации; обобщение выводов.

эмпирические: опросно – диагностические методы (интервьюирование, беседы) и др.;

статистические: анализ статистических данных.

Исследована важность проблемы и сравнены способы решения уравнений второго и выше порядка в различных источниках.

Определена эффективность создания программы решения уравнений второго и выше порядка в системе программирования Pascal ABC.

Оценены перспективы от создания программы.

Теоретическая значимость исследования состоит в разработке алгоритма решения уравнений второго и выше порядка при составлении программы на языке программирования Pascal ABC.

Практическая значимость выводов и рекомендаций, содержащихся в работе, связана с тем, что выполненное исследование направлено на решение конкретной задачи. Работа может быть использована также учителями, проверяющими решение уравнений различных порядков.

Теоретические выводы и практические рекомендации, полученные в результате исследования, могут быть использованы школьниками и учителями различных регионов при решении уравнений второго и выше порядка, а также при составлении программы решения уравнений.

Подготовительный (Подборка и изучение материала по данной теме, выделение проблем. Подборка вопросов для анкетирования)

Анкетирование (Анкетирование учащихся школы по разработанным анкетам)

Обработка анкет и анализ полученных результатов (Работа включает в себя выбор программного обеспечения для обработки анкет. Обработка данных и анализ результатов.)

Разработка алгоритма решения уравнений второго и выше порядка (На этом этапе на основе изученной литературы разрабатывается алгоритм решения уравнений второго и выше порядка.)

Составление и тестирование программы.

Презентация проекта (Представление итогового проекта для обсуждения и оценивания.)

Методы исследования. Анализ информационных источников, статистическая обработка результатов.

Глава 1. Теоретическая часть «Описание математических методов решения уравнений второго и выше порядка»

В настоящее время решение уравнений второго порядка и выше на практике в связи с масштабными затратами времени, выполнение повторных действий заставляет задуматься о составлении программы. В целях обеспечения эффективного решения проблем в области работы с цифрами, когда на любом этапе можно допустить вычислительные ошибки, необходимо создание программы, находящей корни уравнения для проверки собственного решения.

Различные уравнения решали более 25 веков назад. Множество способов решения таких уравнений были созданы в Вавилоне, Индии. Потребность в уравнениях была и будет. Нами приведены способы решения (нахождения корней) квадратных уравнений и уравнений высших степеней. Целое уравнение третьей или более высокой степени в отдельных случаях удается решить, используя точечные приемы. Один из приемов решения уравнения вида Р(х)=), где Р(х) – многочлен, степень которого больше двух, состоит в разложении многочлена на множители. Вспомним, какие способы разложения многочлена на множители мы изучали в 7 классе.

Вынесение общего множителя за скобки

С помощью формул сокращенного умножения

С помощью корней квадратного трехчлена.

В основном это способы решения для уравнений частного характера, то есть в каждой группе уравнений, объединенных какими – либо общими свойствами, приведено особое правило, которое применяется только для этой группы уравнений. Этот способ (подбора к каждому уравнению собственной формулы) гораздо легче, чем нахождение корней через дискриминант. Для деления многочленов применяется правило «деления углом», или схема Горнера.

1.1. Схема Горнера. Возможности.

В этой части нами рассмотрено решения уравнений второго и выше порядка по схеме Горнера. Большинство этих формул решения уравнений частного характера. Эти свойства очень удобны так, как гораздо легче решать уравнения по отдельной формуле для этого уравнения, а не по общему принципу. К каждому из способов мы рассмотрели несколько примеров.

Уильям Джордж Горнер (1786 – 1837), известный по схеме Горнера. Опубликована теорема была в 1815г. в Англии.

Схема Горнера позволяет:

Найти значение многочлена в точке a;

Выяснить, является ли число a – корнем многочлена;

Найти новый многочлен от деления на двучлен (понизить степень);

Используя схему Горнера, мы одновременно проверяем, является ли числоa корнем многочлена и делим этот многочлен на двучлен . Это нам потребуется для понижения степени уравнения и мы сможем воспользоваться вспомогательным алгоритмом.

Выделим существенные правила, которые нам могут пригодиться при решении уравнений второго и выше порядка. Здесь нам помогут такие факты:

Если сумма всех коэффициентов многочлена равна нулю, то число 1 является корнем многочлена.

Если сумма коэффициентов многочлена при четных степеняхравна сумме коэффициентов при нечетных степенях, то число -1 является корнем многочлена.

Для приведенного многочлена степени (из теоремы Виета следует, что) если корни многочлена целые, то они являются делителями его свободного члена, который также является целым числом.

Вывод: Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена. Рассмотрим виды уравнений и вычислим корни.

1.2. Виды уравнений. 1.2.1. Уравнения второй степени (квадратные)

Квадратное уравнение — алгебраическое уравнение 2 — й степени. Общий вид уравнения: . Корни уравнения : Формулы верны при любых коэффициентах.

1.2.2. Уравнения третьей степени (кубические)

Кубическое уравнение — алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ax 3 + bx 2 + cx + d = 0, где а ≠ 0

Используя правила Горнера решим уравнение такого вида. (Приложение 2). Понизив степень многочлена мы продолжаем решение обычного квадратного уравнения, рассмотренного ранее.

1.2.3. Уравнения четвертой степени

Уравнение четвертой степени — алгебраическое уравнение четвертой степени. Общий вид кубического уравнения: аx 4 + bx 3 + cx 2 + dх+е = 0,где а ≠ 0.

Используя схему Горнера решим уравнение этого вида.(Приложение 3). Понизив степень многочлена мы продолжаем решение кубического уравнения, используя схему Горнера, поставив перед собой цель, понизить степень до квадратного уравнения.

В теоретической части нашей работы нами рассмотрены решение квадратных уравнений и уравнений третьей, четвертой степени методом Горнера, определена схема решения уравнений второго, третьего, четвертого порядка, выведены новые, ранее нам неизвестные формулы. Мы проработали много вариантов примеров перед тем, как сделать вывод: используя схему Горнера, мы решаем уравнения третьей, четвертой и выше степеней аналогично. Мы уже представляем себе, как составить программу , которая будет решать уравнения такого вида. Каждое решение пригодится нам в дальнейшей учебе. Эта работа помогла классифицировать старые знания и познать новые.

Глава 2. Экспериментальная часть «Реализация метода Горнера на практике» 2.1. Эксперимент 1. Выявление основных методов решения уравнений второй и выше степени.

Цель: проанализировать основные методы решения уравнений на практике; проанализировать время, которое тратится на решение уравнений второй и выше степени.

Для того чтобы грамотно реализовать собственную программу, необходимо не только ознакомится с мнением, решением, ошибками других, и понять причины, по которым они произошли, но и, возможно, применять особые приемы программирования и специализированные средства разработки.

По результатам анкетирования (приложение 1) учащихся 9 – 11 классов (всего 55 оппонентов) оценки правильного нахождения корней уравнений второго и выше порядка выделено:

Умеют решать квадратные уравнения через дискриминант 50 оппонентов; кубические уравнения делением «уголочком» подбором корней 10 оппонентов; 4 степени подбором корней 3 оппонента и заменой переменной; уравнения выше 4 степени не пробовал решать никто.

Время, которое затрачивается обучающимся на решение уравнений:

Из графика видно, что временные затраты на решение даже одного уравнения существенно. А если их надо решить несколько? Время увеличится в разы.

2.2. Эксперимент 2. Создание алгоритма решения уравнений второго порядка и выше.

Цель: проанализировать эффективность метода Горнера при составлении программы; выработать схему использования вспомогательного алгоритма.

Проанализировав анкеты, мы выяснили, что при решении уравнений второго и выше пличными методами: методом подбора корней, делением уголочком многочлена на многочлен, что довольно долгий процесс решения.

Рассмотренные теоретические вопросы дают возможность создания алгоритма решения поставленной цели. Этот алгоритми будем разрабатывать.

Обращаясь к вспомогательному алгоритму решения квадратного уравнения (приложение 3) и алгоритму «понижения степени» многочлена (нахождения делителей многочлена, разложение многочлена на множители), воспользуемся схемой Горнера. 2.3. Эксперимент 3 . Создание программы, реализующей схему Горнера при решении уравнений второй и выше степени.

Цель: составить программу, позволяющую решать уравнения второй и выше степени; проанализировать работу программы.

Для составления программы мы выбрали среду программирования Pascal ABC. Данная программная среда является языком высокого уровня и в последнее время пользуется не только профессиональными программистами, но и начинающим, а также на уроках информатике и ИКТ в гимназии.

В системе программирования четко реализованы принципы структурного программирования. Сначала мы написали программы отдельно для каждого вида уравнений. Затем воспользовались вспомогательным алгоритмом нахождения квадратного уравнения (приложение 3), кубического уравнения (приложение 4), решили объединить, составили программу с использованием процедуры. Рассмотренные теоретические вопросы дают возможность создания программы на Pascal ABC для решения.

Текст программы решения уравнений второй и выше степени, приведен в приложении 5.

В данной главе рассмотрен алгоритм решения уравнений с использованием схемы Горнера. Составленная программа решения уравнений второй и выше степени может быть использована в практической деятельности для помощи учащимся и учителям решать и проверять соответственно задания , где требуется нахождения корней уравнений второй, третьей, четвертой степени , значительно сократив время на проверку.

Математическая энциклопедия. — М.: Советская энциклопедия.И. М. Виноградов.1977—1985.

В.В. Фараонов «Турбо Паскаль». Издание 7-е переработанное

Интернет http://ru.wikipedia.org «Википедия» — универсальная энциклопедия

Приложение 1 Анкета для обучающихся

Умеете ли Вы решать уравнения вида ах 2 + вх+с=0 (уравнения второго порядка)?

а) да Если «ДА» каким способом _____________________

в) никогда не делал этого ( не встречал в своей жизни)

Сколько занимает времени решение одного уравнения второго порядка?

а) от 1 до 5 минут б) от 5до 10 минут

в) от 10 до 30 минут г) около часа

Умеете ли Вы решать уравнения вида ах 3 + вх 2 +сх+d=0 (уравнения третьего порядка)?

а) да Если «ДА» каким способом ______________________

в) никогда не делал этого ( не встречал в своей жизни)

Сколько занимает времени решение одного уравнения третьего порядка?

а) от 1 до 5 минут б) от 5до 10 минут

в) от 10 до 30 минут г) около часа

Умеете ли Вы решать уравнения вида ах 4 + вх 3 +сх 2 +dx+e=0 (уравнения четвертого порядка)?

а) да Если «ДА» каким способом ______________________

в) никогда не делал этого ( не встречал в своей жизни)

Сколько занимает времени решение одного уравнения четвертого порядка ?

а) от 1 до 5 минут б) от 5до 10 минут

в) от 10 до 30 минут г) около часа

Умеете ли Вы решать уравнения более высокого порядка ?

а) да Если «ДА» каким способом ______________________

в) никогда не делал этого ( не встречал в своей жизни)

Хотели бы Вы научиться решать уравнения второго порядка и выше?

а) да б) нет в) предпочитаю списать

Хотели бы Вы иметь у себя программу, решающую уравнения второго порядка и выше?

Приложение 2 Решение уравнения методом Горнера

Находим делители свободного члена ±1; ± 2; ± 3; ± 6.

Видео:Бином Ньютона максимально простым языкомСкачать

Функция Power

Подпишись на новости, чтобы ничего не пропустить

Функция Power в Паскале (и многих других языках программирования) выполняет возведение числа в степень.

Синтаксис для вещественных чисел:

function Power(Base: Double; Expon: Double) : Double;

Синтаксис для целых чисел:

function Power(Base: LongInt; Expon: LongInt) : LongInt;

Эта функция возводит число Base в степень Expon и возвращает результат. В реальности функция возвращает результат выражения:

Всё, что сказано выше, взято из официальной документации FreePascal. Однако документация иногда расходится с действительностью. Во всяком случае, мой компилятор не соответствует документации. А именно:

В документации сказано, что функция объявлена в модуле SYSTEM. Однако без подключения модуля MATH компилятор выдаёт ошибку. Из этого следует, что на самом деле функция объявлена в модуле MATH.
В документации приведён синтаксис как для целых, так и для вещественных чисел. Однако на самом деле функция работает только с вещественными числами. При попытке использовать целые числа компилятор также выдаёт ошибку.
Возможно, в более новых версиях эти проблемы уже исправлены. Но у меня было именно так (версия FPC 3.0.0).

Видео:Как решать уравнения высших степеней, очень лёгкий способ!!!Скачать

Пример использования функции Power

Пример приведён ниже:

Здесь мы число 2 (переменная Х) возводим в степень 3 (переменная Y), то есть вычисляем следующую формулу:

Обратите внимание на подключенный модуль MATH.

Эта статья входит в раздел о подпрограммах модуля SYSTEM. И по идее описания функции Power здесь не должно быть. Но, так как в документации сказано, что функция Power объявлена в модуле SYSTEM, я решил включить данную статью именно в этот раздел (я же не виноват, что в документации косяк))).

Видео:Степень с натуральным показателем. Свойства степеней. 7 класс.Скачать

Возведение в степень в Паскале

Возведение в степень в Паскале можно выполнить и без какой-то специальной функции, используя функцию вычисления натурального логарифма и функцию вычисления экспоненты. О том, как это сделать, я рассказал здесь.

Однако, если есть специальная функция для возведения числа в степень, то почему бы ей и не воспользоваться? С одной стороны. С другой стороны — эта функция совершенно неожиданно требует подключения модуля MATH.

В документации сказано, что по сути функция Power работает по формуле возведения в степень в Паскале:

Однако, если мы будем делать именно так, эта формула будет неправильно работать с отрицательными числами, потому что в документации сказано, что функция Ln работает только с положительными числами.

Так что функция Power в реальности несколько сложнее, чем приведённая выше формула.

Поэтому для разминки мы напишем свой аналог функции Power, который будет работать правильно. Но для начала вспомним как вычисляется степень числа:

Также напомню, что любое число в нулевой степени равно 1, а ноль в любой степени равен 0 (кроме нуля в нулевой — ноль в нулевой степени не определён, но мы будем возвращать в таких случаях ноль, хотя функция Power возвращает 1).

А теперь наш аналог функции Power:

Я сознательно немного всё усложнил, чтобы вас запутать )))

Пример использования функций Power и её аналога в программе:

Здесь есть один подвох — если вы попытаетесь возвести отрицательное число в не целую степень, например, так:

то стандартная функция Power вызовет ошибку во время выполнения программы. В своём аналоге я этого избежал, но надо понимать, что результат в этом случае будет неправильным (хотя с моей точки зрения это всё-равно лучше, чем аварийное завершение программы).

Это происходит потому, что при таком раскладе результатом являются комплексные числа, а операции с комплексными числами выполняются по другим правилам.

В реальных программах подобные ситуации надо дополнительно обрабатывать (хотя бы предупреждать пользователя о том, что при отрицательном основании и не целой степени функция вернёт неправильный результат).

Ещё в моей функции используется функция Odd, о которой я ещё не рассказывал. Вкратце скажу, что она определяет, является ли число чётным. Более подробно о ней расскажу в отдельной статье.