Говорят что факторы включенные в уравнение регрессии мультиколлинеарны если (7 видео)

Мультиколлинеарность

Содержание

Последствия и признаки мультиколлинеарности
Признаки мультиколлинеарности
Парные (линейные) и частные коэффициенты корреляции
Пошаговая регрессия
Мультиколлинеарность
Матрица парных коэффициентов корреляции
Коллинеарность и мультиколлинеарность факторов во множественной регрессии
🔥 Видео

Видео:Мультиколлинеарность. Алгоритм Фаррара-Глобера. Эконометрика. Регрессия. Multicollinearity.Скачать

Последствия и признаки мультиколлинеарности

Если факторные переменные связаны строгой функциональной зависимостью, то говорят о полной мультиколлинеарности. В этом случае среди столбцов матрицы факторных переменных Х имеются линейно зависимые столбцы, и, по свойству определителей матрицы, det(X T X) = 0 , т. е. матрица (X T X) вырождена, а значит, не существует обратной матрицы. Матрица (X T X) -1 используется в построении МНК-оценок. Таким образом, полная мультиколлинеарность не позволяет однозначно оценить параметры исходной модели регрессии.

Признаки мультиколлинеарности

Регрессионные коэффициенты значительно изменяются по мере удаления или добавления новых предикторов;
Регрессионный коэффициент отрицательный, хотя, исходя из теории, значения зависимой переменной должны расти пропорционально изменению предиктора(или наоборот);
Ни один из коэффициентов не обладает статистической значимостью, однако F-статистика показывает значимость коэффициента детерминации.
Регрессионный коэффициент не является значимым, хотя теоретически связь между ним и зависимой переменной должна быть существенной.
При изменении данных (увеличении или уменьшении выборки) оценки коэффициентов значительно изменяются

К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?

Мультиколлинеарность может привести к нежелательным последствиям:

оценки параметров становятся ненадежными. Они обнаруживают большие стандартные ошибки. С изменением объема наблюдений оценки меняются (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированны; параметры линейной регрессии теряют экономический смысл;
становится невозможным определить изолированное влияние факторов на результативный показатель.

Мультиколлинеарность повышает стандартную ошибку коэффициентов, тем самым искусственно снижая значимость.

Вид мультиколлинеарности, при котором факторные переменные связаны некоторой стохастической зависимостью, называется частичной. Если между факторными переменными имеется высокая степень корреляции, то матрица (X T X) близка к вырожденной, т. е. det(X T X) ≈ 0.
Матрица (X T X) -1 будет плохо обусловленной, что приводит к неустойчивости МНК-оценок. Частичная мультиколлинеарность приводит к следующим последствиям:

увеличение дисперсий оценок параметров расширяет интервальные оценки и ухудшает их точность;
уменьшение t-статистик коэффициентов приводит к неверным выводам о значимости факторов;
неустойчивость МНК-оценок и их дисперсий.

Точных количественных критериев для обнаружения частичной мультиколлинеарности не существует. О наличии мультиколлинеарности может свидетельствовать близость к нулю определителя матрицы (X T X). Также исследуют значения парных коэффициентов корреляции. Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.

Существуют различные подходы преодоления сильной межфакторной корреляции. Простейший из них – исключение из модели фактора (или факторов), в наибольшей степени ответственных за мультиколлинеарность при условии, что качество модели при этом пострадает несущественно (а именно, теоретический коэффициент детерминации -R 2 _{y(x1. xm)} снизится несущественно).

С помощью какой меры невозможно избавиться от мультиколлинеарности?
a) увеличение объема выборки;
b) исключения переменных высококоррелированных с остальными;
c) изменение спецификации модели;
d) преобразование случайной составляющей.

Видео:Множественная регрессия в Excel и мультиколлинеарностьСкачать

Парные (линейные) и частные коэффициенты корреляции

Парный коэффициент корреляции изменяется в пределах от –1 до +1. Чем ближе он по абсолютной величине к единице, тем ближе статистическая зависимость между x и y к линейной функциональной. Положительное значение коэффициента свидетельствует о том, что связь между признаками прямая (с ростом x увеличивается значение y ), отрицательное значение – связь обратная (с ростом x значение y уменьшается).
Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции: если |r| 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.
Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некой генеральной совокупности, вычисленные по этим данным коэффициенты корреляции будут выборочными, т. е. они лишь оценивают связь. Необходима проверка значимости, которая отвечает на вопрос: случайны или нет полученные результаты расчетов.
Значимость парных коэффициентов корреляции проверяют по t-критерию Стьюдента. Выдвигается гипотеза о равенстве нулю генерального коэффициента корреляции: H₀: ρ = 0. Затем задаются параметры: уровень значимости α и число степеней свободы v = n-2. Используя эти параметры, по таблице критических точек распределения Стьюдента находят t_кр, а по имеющимся данным вычисляют наблюдаемое значение критерия:
, (2)
где r – парный коэффициент корреляции, рассчитанный по отобранным для исследования данным. Парный коэффициент корреляции считается значимым (гипотеза о равенстве коэффициента нулю отвергается) с доверительной вероятностью γ = 1- α, если t_Набл по модулю будет больше, чем t_крит.
Если переменные коррелируют друг с другом, то на значении коэффициента корреляции частично сказывается влияние других переменных.

Частный коэффициент корреляции характеризует тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Частный коэффициент корреляции оценивает тесноту связи между двумя переменными при фиксированном значении остальных факторов. Если вычисляется, например, r_yx_1|_x2 (частный коэффициент корреляции между y и x₁ при фиксированном влиянии x₂), это означает, что определяется количественная мера линейной зависимости между y и x₁, которая будет иметь место, если устранить влияние x₂ на эти признаки. Если исключают влияние только одного фактора, получают частный коэффициент корреляции первого порядка.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции r_yx_1|_x2 получится меньше, чем соответствующий парный коэффициент r_yx₁, значит, взаимосвязь признаков y и x₁ в некоторой степени обусловлена воздействием на них фиксируемой переменной x₂. И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная x₂ ослабляет своим воздействием связь y и x₁.
Частный коэффициент корреляции между двумя переменными (y и x₂) при исключении влияния одного фактора (x₁) можно вычислить по следующей формуле:
. (3)
Для других переменных формулы строятся аналогичным образом. При фиксированном x₂
;
при фиксированном x₃
.
Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным v = n – l -2, где l – число фиксируемых факторов.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.

Видео:Эконометрика. Множественная регрессия и корреляция.Скачать

Пошаговая регрессия

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Пример №1 . По 20 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x1 (% от стоимости фондов на конец года) и от ввода в действие новых основных фондов x2 (%).

Y	X1	X2
6	10	3,5
6	12	3,6
7	15	3,9
7	17	4,1
7	18	4,2
8	19	4,5
8	19	5,3
9	20	5,3
9	20	5,6
10	21	6
10	21	6,3
11	22	6,4
11	23	7
12	25	7,5
12	28	7,9
13	30	8,2
13	31	8,4
14	31	8,6
14	35	9,5
15	36	10

Требуется:

Построить корреляционное поле между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации. Выдвинуть гипотезу о тесноте и виде зависимости между показателями X1 и Y .
Оценить тесноту линейной связи между выработкой продукции на одного работника и удельным весом рабочих высокой квалификации с надежностью 0,9.
Рассчитать коэффициенты линейного уравнения регрессии для зависимости выработки продукции на одного работника от удельного веса рабочих высокой квалификации.
Проверить статистическую значимость параметров уравнения регрессии с надежностью 0,9 и построить для них доверительные интервалы.
Рассчитать коэффициент детерминации. С помощью F -критерия Фишера оценить статистическую значимость уравнения регрессии с надежностью 0,9.
Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих.
Рассчитать коэффициенты линейного уравнения множественной регрессии и пояснить экономический смысл его параметров.
Проанализировать статистическую значимость коэффициентов множественного уравнения с надежностью 0,9 и построить для них доверительные интервалы.
Найти коэффициенты парной и частной корреляции. Проанализировать их.
Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
С помощью F -критерия Фишера оценить адекватность уравнения регрессии с надежностью 0,9.
Дать точечный и интервальный прогноз с надежностью 0,9 выработки продукции на одного работника для предприятия, на котором высокую квалификацию имеют 24% рабочих, а ввод в действие новых основных фондов составляет 5%.
Проверить построенное уравнение на наличие мультиколлинеарности по: критерию Стьюдента; критерию χ2. Сравнить полученные результаты.

Решение проводим с помощью калькулятора. Далее приводится ход решения п.13.
Матрица парных коэффициентов корреляции R:

—	y	x₁	x₂
y	1	0.97	0.991
x₁	0.97	1	0.977
x₂	0.991	0.977	1

При наличии мультиколлинеарности определитель корреляционной матрицы близок к нулю. Для нашего примера: det = 0.00081158 , что свидетельствует о наличии сильной мультиколлинеарности.
Для отбора наиболее значимых факторов x_i учитываются следующие условия:
— связь между результативным признаком и факторным должна быть выше межфакторной связи;
— связь между факторами должна быть не более 0.7. Если в матрице есть межфакторный коэффициент корреляции r_xjxi > 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.;
— при высокой межфакторной связи признака отбираются факторы с меньшим коэффициентом корреляции между ними.
В нашем случае r_{x₁ x₂} имеют |r|>0.7, что говорит о мультиколлинеарности факторов и о необходимости исключения одного из них из дальнейшего анализа.
Анализ первой строки этой матрицы позволяет произвести отбор факторных признаков, которые могут быть включены в модель множественной корреляционной зависимости. Факторные признаки, у которых |r_yxi| 0.3 – связь практически отсутствует; 0.3 ≤ |r| ≤ 0.7 — связь средняя; 0.7 ≤ |r| ≤ 0.9 – связь сильная; |r| > 0.9 – связь весьма сильная.
Проверим значимость полученных парных коэффициентов корреляции с помощью t-критерия Стьюдента. Коэффициенты, для которых значения t-статистики по модулю больше найденного критического значения, считаются значимыми.
Рассчитаем наблюдаемые значения t-статистики для r_yx₁по формуле:

где m = 1 — количество факторов в уравнении регрессии.

По таблице Стьюдента находим Tтабл
t_крит(n-m-1;α/2) = (18;0.025) = 2.101
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
Рассчитаем наблюдаемые значения t-статистики для r_yx₂по формуле:

Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значимю
Таким образом, связь между (y и x_x₁), (y и x_x₂) является существенной.
Наибольшее влияние на результативный признак оказывает фактор x₂ (r = 0.99), значит, при построении модели он войдет в регрессионное уравнение первым.
Тестирование и устранение мультиколлинеарности.
Наиболее полным алгоритмом исследования мультиколлинеарности является алгоритм Фаррара-Глобера. С его помощью тестируют три вида мультиколлинеарности:
1. Всех факторов (χ 2 — хи-квадрат).
2. Каждого фактора с остальными (критерий Фишера).
3. Каждой пары факторов (критерий Стьюдента).
Проверим переменные на мультиколлинеарность методом Фаррара-Глоубера по первому виду статистических критериев (критерий «хи-квадрат»).
Формула для расчета значения статистики Фаррара-Глоубера:
χ 2 = -[n-1-(2m+5)/6]ln(det[R])
где m = 2 — количество факторов, n = 20 — количество наблюдений, det[R] — определитель матрицы парных коэффициентов корреляции R.
Сравниваем его с табличным значением при v = m/2(m-1) = 1 степенях свободы и уровне значимости α. Если χ 2 > χ_табл 2 , то в векторе факторов есть присутствует мультиколлинеарность.
χ_табл 2 (1;0.05) = 3.84146
Проверим переменные на мультиколлинеарность по второму виду статистических критериев (критерий Фишера).
Определяем обратную матрицу D = R -1 :

D =

55,365	-2,256	-52,656
-2,256	22,386	-19,642
-52,656	-19,642	72,373

Вычисляем F-критерии Фишера:

где d_kk — диагональные элементы матрицы.
Рассчитанные значения критериев сравниваются с табличными при v₁=n-m и v₂=m-1 степенях свободы и уровне значимости α. Если F_k > F_Табл, то k-я переменная мультиколлинеарна с другими.
v₁=20-2 = 18; v₂=2-1 = 1. F_Табл(18;1) = 248

Поскольку F₁ > F_табл, то переменная y мультиколлинеарна с другими.

Поскольку F₂ > F_табл, то переменная x₁ мультиколлинеарна с другими.

Поскольку F₃ > F_табл, то переменная x₂ мультиколлинеарна с другими.

Проверим переменные на мультиколлинеарность по третьему виду статистических критериев (критерий Стьюдента). Для этого найдем частные коэффициенты корреляции.
Частные коэффициенты корреляции.
Коэффициент частной корреляции отличается от простого коэффициента линейной парной корреляции тем, что он измеряет парную корреляцию соответствующих признаков (y и x_i) при условии, что влияние на них остальных факторов (x_j) устранено.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.

Теснота связи низкая.
Определим значимость коэффициента корреляции r_{yx₁ /x₂}.
Для этого рассчитаем наблюдаемые значения t-статистики по формуле:

где k = 1 — число фиксируемых факторов.

По таблице Стьюдента находим Tтабл
t_крит(n-k-2;α/2) = (17;0.025) = 2.11
Поскольку t_набл t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
Как видим, связь y и x₂ при условии, что x₁ войдет в модель, снизилась. Отсюда можно сделать вывод, что ввод в регрессионное уравнение x₂ остается нецелесообразным.
Можно сделать вывод, что при построении регрессионного уравнения следует отобрать факторы x₁ , x₂.

Видео:Математика #1 | Корреляция и регрессияСкачать

Мультиколлинеарность

Коэффициенты интеркорреляции (т. е. сила связи между объясняющими переменными) позволяют исключить из модели регрессии дублирующие факторы. Две переменных явно коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции > 0,7.

Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение в эконометрике отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеет наименьшую тесноту связи с другими факторами. Т.е. коэффициент корреляции между факторами меньше 0,3 или, в идеале, близок к нулю. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.

Видео:Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Матрица парных коэффициентов корреляции

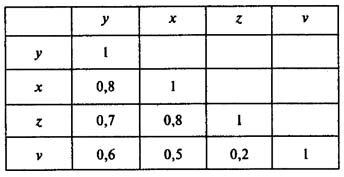
Пусть, например, при изучении зависимости у = f(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:

Факторы х и z дублируют друг друга, т.к. связь между ними сильная (больше 0,7). В анализ нужно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора х с у, но значительно слабее межфакторная связь Rzv

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Коллинеарность и мультиколлинеарность факторов во множественной регрессии

Под мультиколлинеарностью понимают взаимосвязь двух или нескольких объясняющих переменных. Если объясняющие переменные связаны строгой функциональной зависимостью, то говорят о совершенной мультиколлинеарности. На практике высокая (или близкая к ней) мультиколлинеарность может стать проблемой при построении множественной регрессии. Поясним это на примере совершенной мультиколлинеарности.

Предположим, что искомое уравнение регрессии имеет

а между объясняющими переменными существует строгая линейная зависимость

Подставив (107) в (108), получим или

Далее, обозначив Р₀ + р₂у₀ = а; Р, + Р₂у, = Ь. получаем уравнение парной линейной регрессии:

Воспользовавшись МНК, можно определить коэффициенты а и b. Тогда для определения истинных коэффициентов регрессии получим систему из двух уравнений:

в которую входят три неизвестных величины: Р₀, p,_f р₂. Такая система и подавляющем числе случаев имеет бесконечно много решений. Таким образом, совершенная мультиколлинеарность не позволяет однозначно определить коэффициенты регрессии уравнения (107) и разделить вклады объясняющих переменных X, и Х₂ в их влиянии на зависимую переменную У. В этом случае невозможно сделать обоснованные статистические выводы об этих коэффициентах. Следовательно, в случае мультиколлинеарности выводы по коэффициентам и по самому уравнению регрессии будут ненадежными.

Естественно, что мультиколлинеарность в реальных ситуациях проявляется не как функциональная, а как сильная корреляционная зависимость между объясняющими переменными. Поэтому ее можно охарактеризовать значением коэффициента корреляции р между соответствующими объясняющими переменными. Причем, чем ближе абсолютное значение р к единице, тем совершеннее мультиколлинеарность.

Как мы уже показали аналитически, мультиколлинеарность затрудняет разделение влияния факторов на зависимую переменную и делает оценки коэффициентов регрессии ненадежными. Наглядно это подтверждается с помощью диаграммы Венна (рис. 10).

Если коррелированность между объясняющими переменными X, и Х₂ отсутствует (рис. 10, а), то влияние каждой из них на У отражается не перекрывающимися частями кругов Х_< и Х₂ в круге У. По мере усиления связи между и Х₂ соответствующие круги все больше накладываются друг на друга (заштрихованная область на рис. 10, б, в). Наконец, при совершенной мультиколлинеарности (рис. 10. г), невозможно разграничить степени индивидуального влияния объясняющих переменных X, и Х₂ на зависимую переменную У. В итоге могут проявиться следующие последствия мультиколлинеарности.

1. Возрастают дисперсии (стандартные ошибки) оценок коэффициентов регрессии, что расширяет доверительные интервалы оценки и ухудшает точность модели.
2. Уменьшаются ^-статистики коэффициентов, что может привести к неоправданному выводу о существенности влияния объясняющей переменной на результирующий показатель.
3. Оценки коэффициентов по методу наименьших становятся очень чувствительными к малейшим изменениям данных, т. е. они становятся неустойчивыми.
4. Определить вклад каждой из объясняющих переменных в изменчивость зависимой переменной практически невозможно, причем, не исключается даже получение неверного знака у коэффициентов регрессии.

Для выявления мультиколлинеарности можно использовать несколько признаков.

Во-первых, в этом случае коэффициент детерминации R 2 достаточно высок, но некоторые из коэффициентов регрессии статистически незначимы (имеют низкие f-статистики).

Во-вторых, парная корреляция между малозначимыми объясняющими переменными достаточно высока. Следует, однако, учитывать, что данный признак будет надежным лишь в случае двух объясняющих переменных. При большем их количестве целесообразнее анализировать частные коэффициенты корреляции, которые определяют силу линейной зависимости между двумя переменными без учета влияния на них других переменных.

В-третьих, проявляется сильная вспомогательная (дополнительная) регрессия, увеличивающая коэффициент детерминации.

Чаще всего для оценки степени мультиколлинеарности используют расчет определителя матрицы парных коэффициентов корреляции.

Если факторы модели не взаимосвязаны, то матрица парных коэффициентов корреляции должна быть единичной, поскольку все ее недиагональные элементы в этом случае равны нулю. К примеру, для включающей три переменных регрессионной модели

матрица коэффициентов корреляции между факторами имела бы определитель:

поскольку г_„ = Г = г _х = 1 и г = г =г = 0.

Следовательно, чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность и ненадежнее выводы по построенной множественной регрессии.

Поскольку значение определителя остается величиной случайной, то проверку на мультиколлинеарность проводят по критерию х 2 Для гипотезы H_Q: Det|R| = 1. Доказано, что величина

имеет распределение х 2 с числом степеней свободы Если фактическое значение х 2 превосходит табличное (критическое) Хфакт > Х?абл«*.о) • то

гипотеза Н₀ отклоняется и мультиколлинеарность исследуемых факторов считается доказанной, а, следовательно, и избранная форма модели должна быть признана неадекватной.

Отметим, что в ряде случаев мультиколлинеарность не является таким уж серьезным «злом», чтобы прилагать существенные усилия по ее выявлению и устранению. В основном все зависит от целей исследования.

Если основная задача модели — прогноз будущих значений зависимой переменной, то при достаточно болыиом коэффициенте детерминации Я 2 (? 0,9) наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели. Хотя это утверждение будет обоснованным лишь в том случае, что и в будущем между коррелированными переменными будут сохраняться те же отношения, что и ранее.

Если же целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую переменную, то наличие мультиколлинеарности, приводящее к увеличению стандартных ошибок, исказит истинные зависимости между переменными и мультиколлинеарность станет серьезной проблемой.

Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных. Необходимо, однако, сохранять соответствие спецификации модели общетеоретическим представлениям.

Далее, поскольку мультиколлинеарность напрямую зависит от выборки, то целесообразно проверить модель и на других данных. Возможно, что при другой выборке мультиколлинеарность не будет столь серьезной. Иногда достаточно просто увеличить объем выборки. Увеличение количества данных сокращает дисперсии коэффициентов регрессии и тем самым увеличивает их статистическую значимость.

Зачастую при построении модели множественной регрессии можно воспользоваться предварительной информацией, в частности, известными значениями некоторых коэффициентов регрессии. Для иллюстрации приведем следующий пример. Предположим, что строится регрессия вида (107), но оказалось, что переменные Х₁ и Х₂ коррелированны. Если на предварительном этапе исследования для парной регрессии У = у₀ + у,Х, + v был определен статистически значимый коэффициент у, (для определенности пусть Yi =0,8), связывающий Ус X,, и есть основания считать, что связь между У и X, останется неизменной, то можно положить y_t = Р, = 0,8. Тогда (107) примет вид:

В результате уравнение (111) фактически представляет парную регрессию, для которой проблема мультиколлинеарности не существует.

В ряде случаев минимизировать либо вообще устранить проблему мультиколлинеарности можно с помощью преобразования переменных.

Например, пусть эмпирическое уравнение регрессии имеет вид

причем, X, и Х₂ — коррелированные переменные. В этой ситуации можно попытаться построить регрессионные зависимости для относительных величин:

Не исключено, что в новой модели проблема мультиколлинеарности будет отсутствовать.

Возможны и другие преобразования, близкие по своей сути к вышеописанным. Например, если в уравнении рассматриваются взаимосвязи номинальных экономических показателей, то для снижения мультиколлинеарности можно попытаться перейти к реальным показателям и т. п.