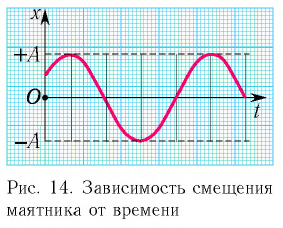
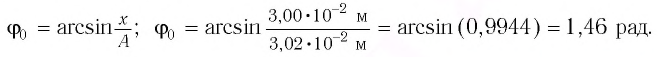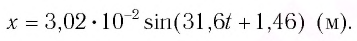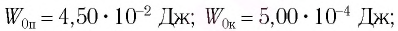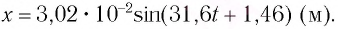Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
| . |
В этом соотношении – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:
| . |
Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими .
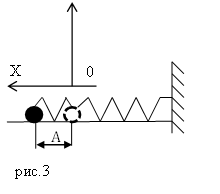
Таким образом, груз некоторой массы , прикрепленный к пружине жесткости , второй конец которой закреплен неподвижно (рис. 2.2.1), составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором .
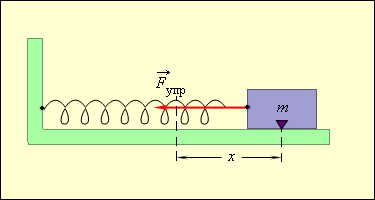 | |||||||||||||||||||
| Рисунок 2.2.1. Круговая частота свободных колебаний груза на пружине находится из второго закона Ньютона:
откуда
Частота называется собственной частотой колебательной системы. Период гармонических колебаний груза на пружине равен
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину , равную
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты и периода колебаний справедливы и в этом случае. Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела и координатой : ускорение является второй производной координаты тела по времени :
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде
или
где Все физические системы (не только механические), описываемые уравнением (*), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида
Уравнение (*) называется уравнением свободных колебаний . Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний или период . Такие параметры колебательного процесса, как амплитуда m и начальная фаза , определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени. Если, например, груз был смещен из положения равновесия на расстояние и затем в момент времени отпущен без начальной скорости, то m = , . Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость Таким образом, амплитуда m свободных колебаний и его начальная фаза определяются начальными условиями . Существует много разновидностей механических колебательных систем, в которых используются силы упругих деформаций. На рис. 2.2.2 показан угловой аналог линейного гармонического осциллятора, совершающий крутильные колебания. Горизонтально расположенный диск висит на упругой нити, закрепленной в его центре масс. При повороте диска на угол возникает момент сил упругой деформации кручения:
Это соотношение выражает закон Гука для деформации кручения. Величина аналогична жесткости пружины . Второй закон Ньютона для вращательного движения диска записывается в виде (см. §1.23)
где – момент инерции диска относительно оси, проходящий через центр масс, – угловое ускорение. По аналогии с грузом на пружине можно получить:
Крутильный маятник широко используется в механических часах. Его называют балансиром. В балансире момент упругих сил создается с помощью спиралевидной пружинки. Содержание
Видео:9 класс, 34 урок, Колебания математического маятника и груза на пружинеСкачать  Формулы пружинного маятникаВидео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  Определение и формулы пружинного маятникаПружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз. Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе. Видео:колебания груза на пружинеСкачать  Уравнения колебаний пружинного маятникаПружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид: где $^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция: где $_0=sqrt<frac>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний. В экспоненциальном виде колебания пружинного маятника можно записать как: [Re tilde=Releft(Acdot exp left(ileft(_0t+varphi right)right)right)left(3right).] Видео:Грузы на пружинах.Скачать  Формулы периода и частоты колебаний пружинного маятникаЕсли в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы: Так как частота колебаний ($nu $) — величина обратная к периоду, то: Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  Формулы амплитуды и начальной фазы пружинного маятникаЗная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $). Амплитуду можно найти как: начальная фаза при этом: где $v_0$ — скорость груза при $t=0 c$, когда координата груза равна $x_0$. Видео:ОГЭ ЕГЭ 2021 Математика Прикладная задача о колебании груза на пружинеСкачать  Энергия колебаний пружинного маятникаПри одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии. Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис.2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат. Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая: учитывая, что для пружинного маятника $F=-kx$, тогда потенциальная энергия ($E_p$) пружинного маятника равна: Закон сохранения энергии для пружинного маятника запишем как: где $dot=v$ — скорость движения груза; $E_k=frac<m<dot>^2>$ — кинетическая энергия маятника. Из формулы (10) можно сделать следующие выводы:
Видео:Гармонический осциллятор. Груз на пружине. 3 метода решения.Скачать  Примеры задач с решениемЗадание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac$? Решение. Сделаем рисунок. По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем: где $E_$ — потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_$ — кинетическая энергия шарика, в момент прохождения положения равновесия. Потенциальная энергия равна: В соответствии с (1.1) приравняем правые части (1.2) и (1.3), имеем: Из (1.4) выразим искомую величину: Вычислим начальное (максимальное) смещение груза от положения равновесия: Ответ. $x_0=1,5$ мм Задание. Пружинный маятник совершает колебания по закону: $x=A $где $A$ и $omega $ — постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_$. В какой момент времени это произойдет? Решение. Возвращающей силой для пружинного маятника является сила упругости, равная: Потенциальную энергию колебаний груза найдем как: В момент времени, который следует найти $F=F_0$; $E_p=E_$, значит: Видео:Математические и пружинные маятники. 11 класс.Скачать  Гармонические колебания в физике — формулы и определение с примерамиСодержание: Гармонические колебания: Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием. Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением ( Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня. Если груз, который находится в равновесии, потянем вправо на расстояние С течением времени смещение груза уменьшается относительно здесь: Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями. Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений. Видео:Физика Груз, колеблющийся на пружине, за 8 с совершил 32 колебания. Найдите период и частотуСкачать  Основные параметры гармонических колебанийa) период колебания
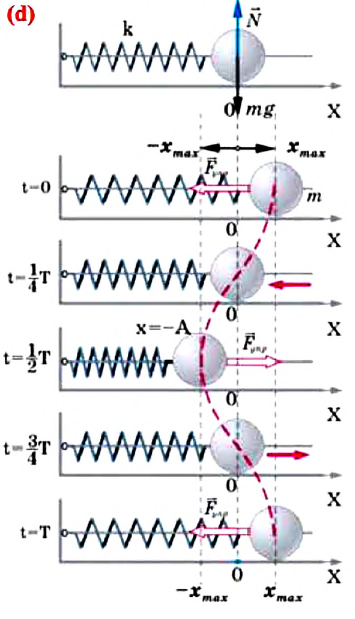
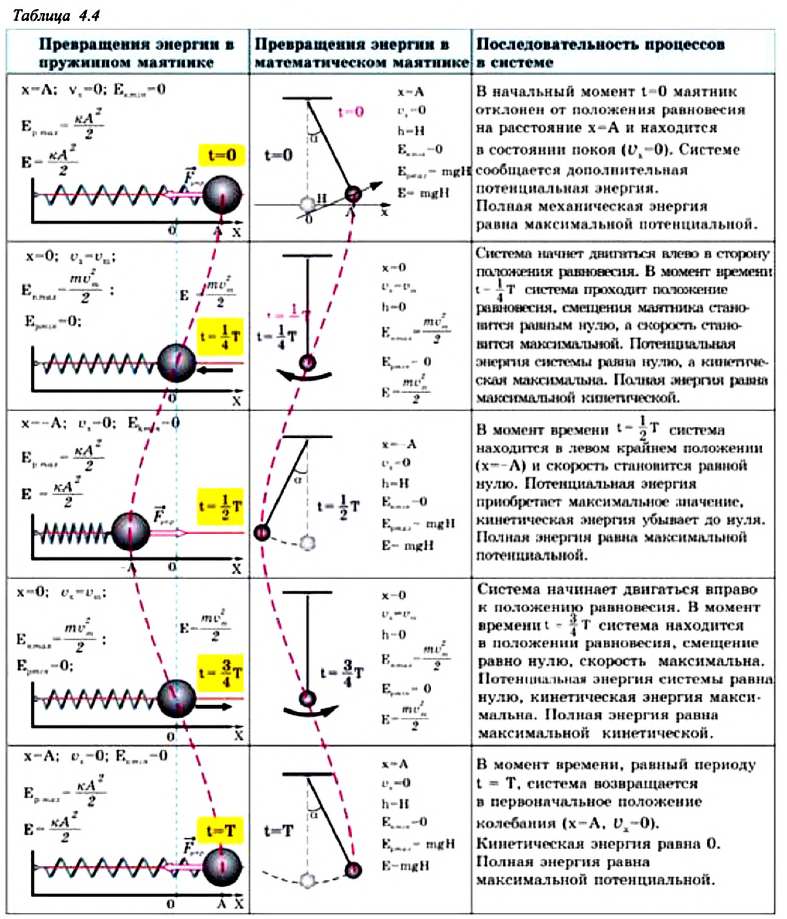
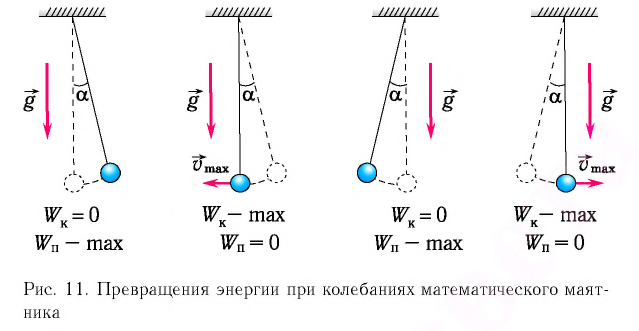
б) частота колебания Единица С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме. Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются. Пример решения задачи: Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м. Формула и решение: Видео:Колебания груза на вертикальной пружинеСкачать  Гармонические колебания пружинного маятникаВ 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний. Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник. Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями: Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения. Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой. С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d). В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника. Где Таким образом, уравнение движения пружинного маятника можно записать и так: Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями. Здесь Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника: Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему. Видео:Урок 92 (осн). Колебательное движение. МаятникиСкачать  Гармонические колебания математического маятникаДо наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника. Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника. Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити. Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b). Сила тяжести Приняв во внимание, что: Для уравнения движения математического маятника получим: Где Для данной колебательной системы отношение Таким образом, уравнение движения математического маятника можно записать и так: Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция: Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями. Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника: Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке. Скорость и ускорение при гармонических колебанияхВы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания. При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю Так как скорость является первой производной смещения (координат) по времени, то: Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний: Так как ускорение является первой производной скорости по времени, то получим: Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на Превращения энергии при гармонических колебанияхТеоретический материалПотенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга. В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения Если же маятник находится в точке равновесия, потенциальная энергия минимальна: Кинетическая энергия системы, наоборот, в точке возвращения минимальна На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения. Полная механическая энергия замкнутой колебательной системы в произвольный момент времени a) для пружинного маятника: b) для математического маятника: Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b): Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону: • Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний. Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают: Превращения энергии при гармонических колебанияхМеханическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется. Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю. При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна: Из закона сохранения механической энергии следует (рис. 8), что
Отсюда найдем модуль максимальной скорости маятника: Высоту Если колебания малые, то Подставив выражение для Подставляя выражения для Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную. В любом промежуточном положении Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний. В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза: где В промежуточных точках полная механическая энергия Отсюда можно вывести выражение для модуля скорости Так как Энергия при гармонических колебанияхМеханическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется. Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю. При отклонении маятника на угол Поскольку при прохождении положения равновесия потенциальная энергия равна нулю Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии: Отсюда найдем модуль максимальной скорости маятника: Высоту или Подставив выражение (3) для Подставляя выражения (3) для Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12). В крайних положениях, когда Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний. В положении равновесия, когда где В положениях между крайними точками полная энергия С учетом выражений для координаты Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная: Таким образом, начальное смещение Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13). Пример №1 Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние
По закону сохранения механической энергии
Пример №2 Груз массой
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний: Отсюда Ответ:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 📺 ВидеоФизика Найдите массу груза, который за 16 с совершил 20 колебаний на пружине жесткостью 250 Н/м.Скачать  Груз на пружине. Две формулы.Скачать  Колебания груза на пружине: 2 задачиСкачать  5.4 Уравнение гармонических колебанийСкачать  Колебания математического и пружинного маятников. 9 класс.Скачать  Физика Груз массой 400 г совершает колебания на пружине жесткостью 250 Н/м. Амплитуда колебаний 15Скачать  Колебание груза пружинеСкачать  Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать  Урок 330. Скорость и ускорение при гармонических колебанияхСкачать  |
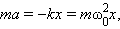
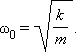
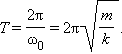
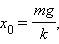
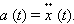
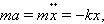
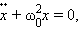
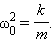
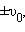 то
то 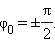
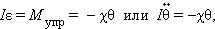
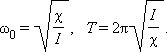
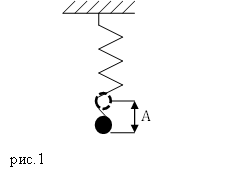
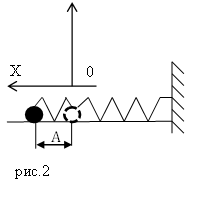
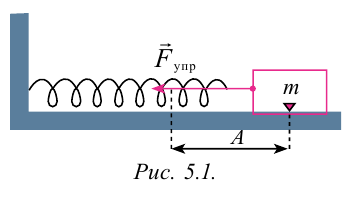
 , а ее масса ничтожна мала и можно ее не учитывать. Считаем, что масса системы сосредоточена в грузе, а упругость в пружине.
, а ее масса ничтожна мала и можно ее не учитывать. Считаем, что масса системы сосредоточена в грузе, а упругость в пружине.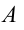 и отпустим, то под действием силы упругость, которая появляется в пружине, груз смещается в
и отпустим, то под действием силы упругость, которая появляется в пружине, груз смещается в 
 , но скорость груза при этом увеличивается. Когда груз доходит до равновесного состояния, его смещение (
, но скорость груза при этом увеличивается. Когда груз доходит до равновесного состояния, его смещение (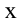 ) равняется нулю и соответственно сила упругости равняется нулю. Но груз по инерции начинает двигаться в левую сторону. Модуль силы упругости, которая появляется в пружине, тоже растет. Однако из-за того, что сила упругости постоянно направлена против смещения груза, она начинает тормозить груз. В результате движение груза замедляется, и, в результате, прекращается. Теперь груз под воздействием эластической силы сжатой пружины начинает двигаться в сторону равновесного состояния.
) равняется нулю и соответственно сила упругости равняется нулю. Но груз по инерции начинает двигаться в левую сторону. Модуль силы упругости, которая появляется в пружине, тоже растет. Однако из-за того, что сила упругости постоянно направлена против смещения груза, она начинает тормозить груз. В результате движение груза замедляется, и, в результате, прекращается. Теперь груз под воздействием эластической силы сжатой пружины начинает двигаться в сторону равновесного состояния. 
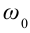 – циклическая частота, зависящая от параметров колеблющихся систем,
– циклическая частота, зависящая от параметров колеблющихся систем, 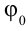 – начальная фаза, (
– начальная фаза, (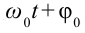 ) фаза колебания с течением времени
) фаза колебания с течением времени 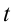 .
. 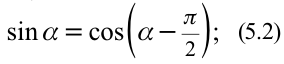 поэтому формулу (5.2.) можно записать в виде
поэтому формулу (5.2.) можно записать в виде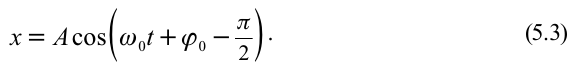
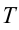 – время одного полного колебания:
– время одного полного колебания: )
)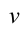 – количество колебаний, совершаемых за 1 секунду:
– количество колебаний, совершаемых за 1 секунду:
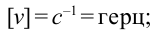
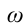 – количество колебаний за
– количество колебаний за 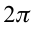 секунд:
секунд:
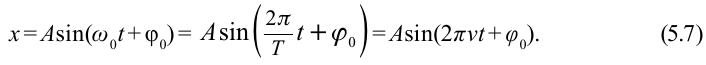
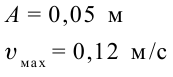
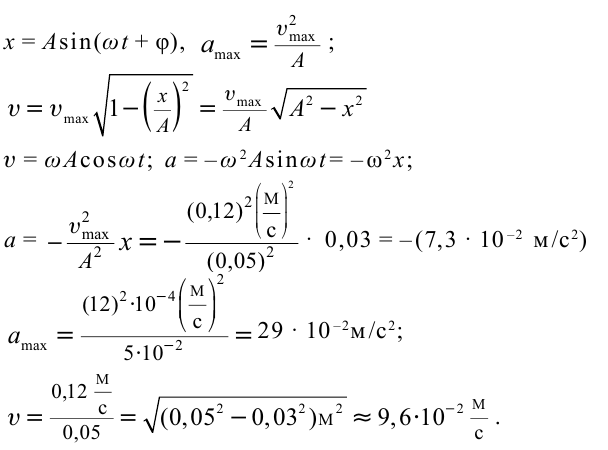
 сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:
сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так: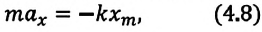
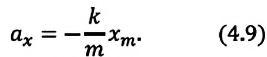
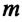 — масса шарика, закрепленного на пружине,
— масса шарика, закрепленного на пружине, 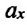 — проекция ускорения шарика вдоль оси
— проекция ускорения шарика вдоль оси 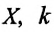 — жесткость пружины,
— жесткость пружины, 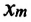 -удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение
-удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение 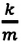 — постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения — известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение
— постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения — известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение 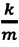 соответствует квадрату циклической частоты
соответствует квадрату циклической частоты 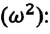
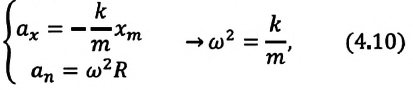
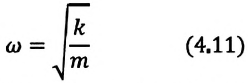
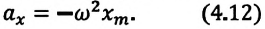
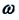 являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:
являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является: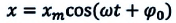
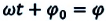 фаза колебания,
фаза колебания, 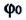 — начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах:
— начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах: 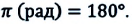 Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы
Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы 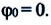 В этом случае формулу гармонических колебаний пружинного маятника можно записать так:
В этом случае формулу гармонических колебаний пружинного маятника можно записать так: или
или 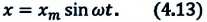
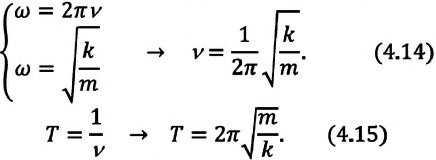
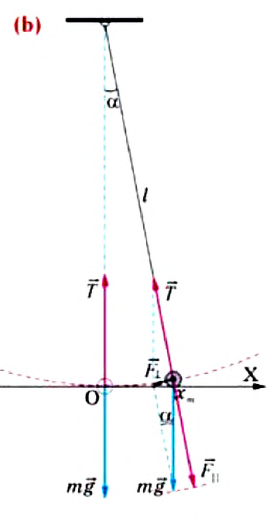
 действующая на шарик в положении равновесия маятника, уравновешивается силой натяжения нити
действующая на шарик в положении равновесия маятника, уравновешивается силой натяжения нити  Однако, если вывести маятник из состояния равновесия, сместив его на малый угол
Однако, если вывести маятник из состояния равновесия, сместив его на малый угол  в сторону, то возникают две составляющие вектора силы тяжести -направленная вдоль нити
в сторону, то возникают две составляющие вектора силы тяжести -направленная вдоль нити 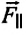 и перпендикулярная нити
и перпендикулярная нити 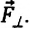 Сила натяжения
Сила натяжения 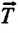 и составляющая силы тяжести
и составляющая силы тяжести 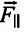 уравновешивают друг друга. Поэтому равнодействующая сила будет равна составляющей
уравновешивают друг друга. Поэтому равнодействующая сила будет равна составляющей 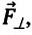 «пытающейся» вернуть тело в положение равновесия (см.: рис. b). Учитывая вышеуказанное и ссылаясь на II закон Ньютона, можно написать уравнение колебательного движения тела массой
«пытающейся» вернуть тело в положение равновесия (см.: рис. b). Учитывая вышеуказанное и ссылаясь на II закон Ньютона, можно написать уравнение колебательного движения тела массой 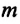 в проекциях на ось ОХ:
в проекциях на ось ОХ: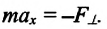
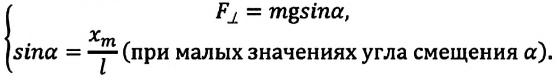
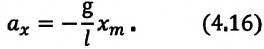
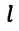 — длина математического маятника (нити),
— длина математического маятника (нити), 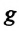 — ускорение свободного падения,
— ускорение свободного падения, 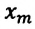 — амплитуда колебания.
— амплитуда колебания. — постоянная положительная величина, потому что ускорение свободного падения и длина нити не могут быть отрицательными. Если сравнить уравнения (4.16) и (4.10), с легкостью можно увидеть, что отношение
— постоянная положительная величина, потому что ускорение свободного падения и длина нити не могут быть отрицательными. Если сравнить уравнения (4.16) и (4.10), с легкостью можно увидеть, что отношение 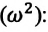


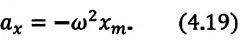
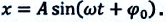
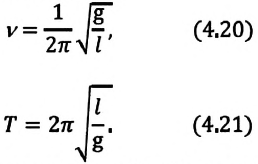
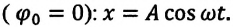
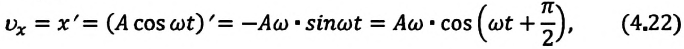
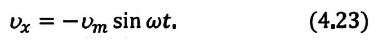
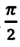 (а).
(а).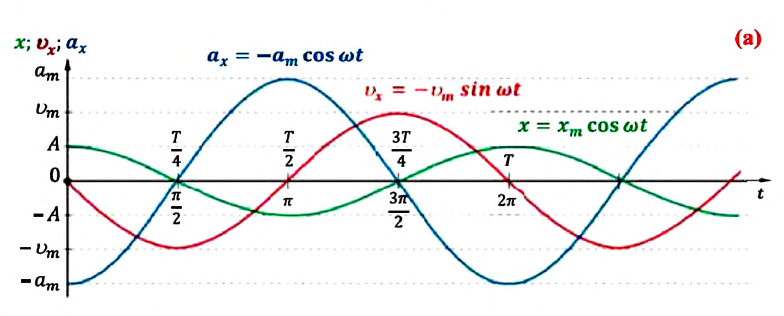
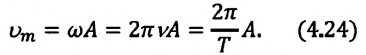
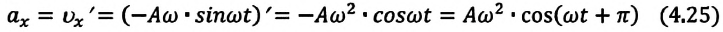

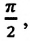 а колебания смещения на
а колебания смещения на (см.: рис. а). Максимальное (амплитудное) значение ускорения зависит от амплитуды, частоты и периода колебаний:
(см.: рис. а). Максимальное (амплитудное) значение ускорения зависит от амплитуды, частоты и периода колебаний: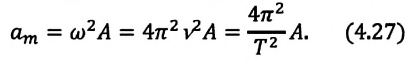
 имеет максимальное значение:
имеет максимальное значение: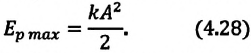
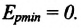
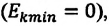 а в точке равновесия максимальна:
а в точке равновесия максимальна: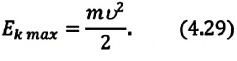
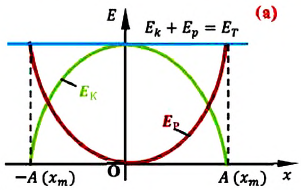
 остается постоянной (трение не учитывается):
остается постоянной (трение не учитывается):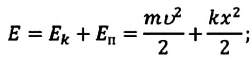
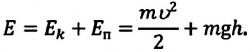
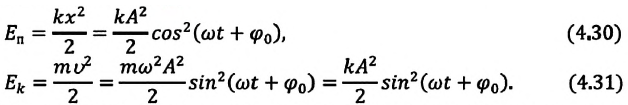
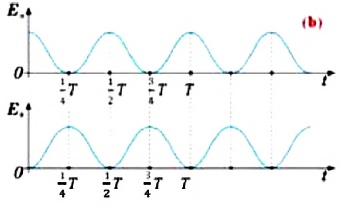
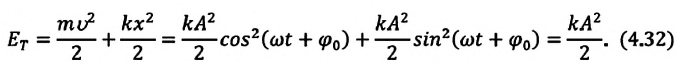
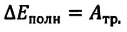
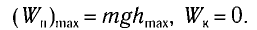
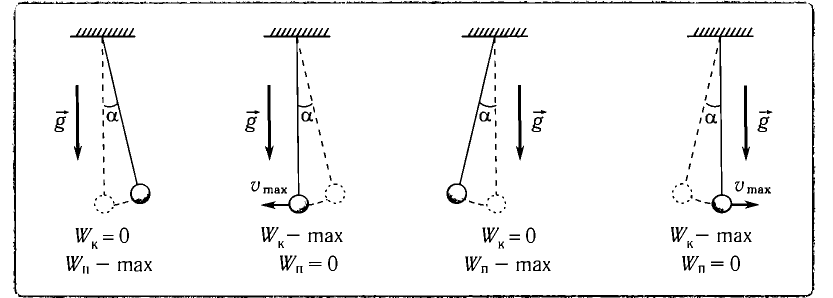
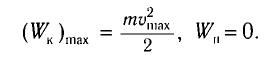
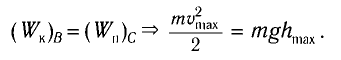 (1)
(1)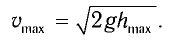 (2)
(2) можно выразить через длину маятника l и амплитуду колебаний А.
можно выразить через длину маятника l и амплитуду колебаний А.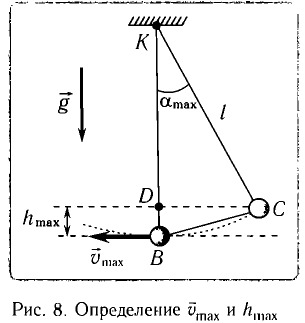
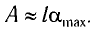 Из треугольника KCD на рисунке 8 находим
Из треугольника KCD на рисунке 8 находим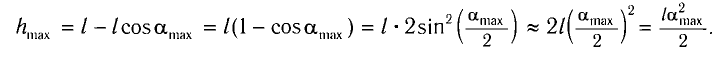
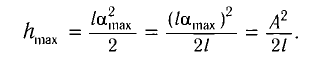
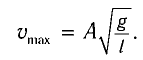
 и
и 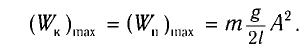
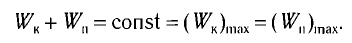
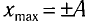 , модуль его скорости равен нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:
, модуль его скорости равен нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины: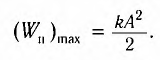
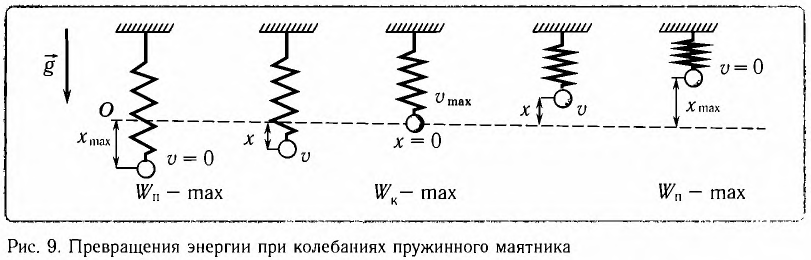
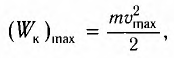
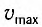 — модуль максимальной скорости груза при колебаниях.
— модуль максимальной скорости груза при колебаниях.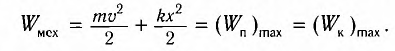
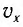 груза в точке с
груза в точке с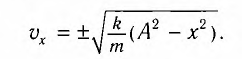
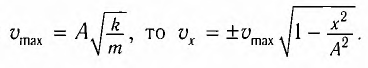
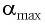 (рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
(рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю: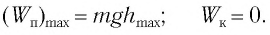
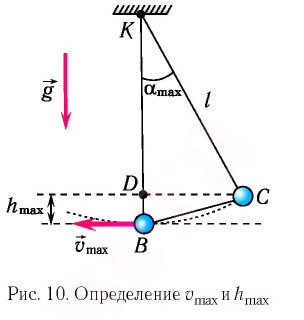
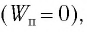 то из закона сохранения механической энергии следует (см. рис. 10), что
то из закона сохранения механической энергии следует (см. рис. 10), что 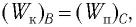 т. е. кинетическая энергия маятника (а следовательно, и скорость) рис. ю. Определение^иhmax будет максимальна:
т. е. кинетическая энергия маятника (а следовательно, и скорость) рис. ю. Определение^иhmax будет максимальна: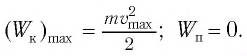
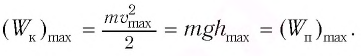
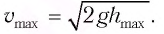
 можно выразить через длину
можно выразить через длину  маятника и амплитуду
маятника и амплитуду 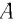 колебаний. Если колебания малые, то
колебаний. Если колебания малые, то 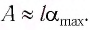 Из
Из 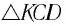 (см. рис. 10) находим:
(см. рис. 10) находим: 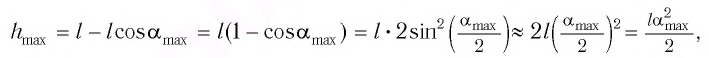
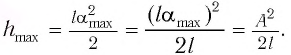
 в формулу (2), получим:
в формулу (2), получим: 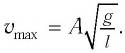
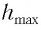 и (4) для
и (4) для 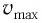 в соотношение (1), находим:
в соотношение (1), находим: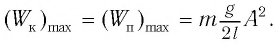
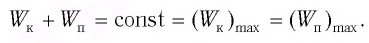
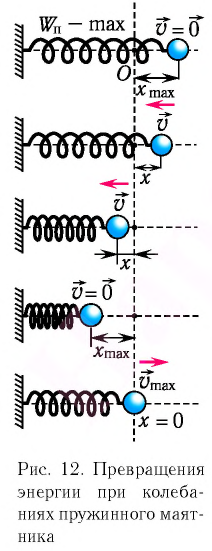
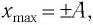 модуль скорости маятника
модуль скорости маятника 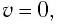 и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:
и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины: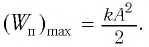
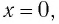 вся энергия пружинного маятника переходит в кинетическую энергию груза:
вся энергия пружинного маятника переходит в кинетическую энергию груза: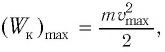
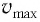 — модуль максимальной скорости груза при колебаниях.
— модуль максимальной скорости груза при колебаниях.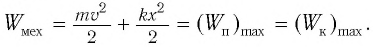
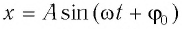 и проекции скорости груза
и проекции скорости груза 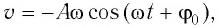 а также для
а также для 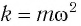 находим его потенциальную энергию
находим его потенциальную энергию 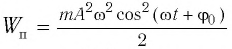 и кинетическую энергию
и кинетическую энергию 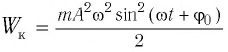 в произвольный момент времени
в произвольный момент времени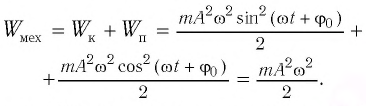
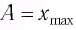 определяет начальную потенциальную, а начальная скорость
определяет начальную потенциальную, а начальная скорость 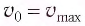 определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.
определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.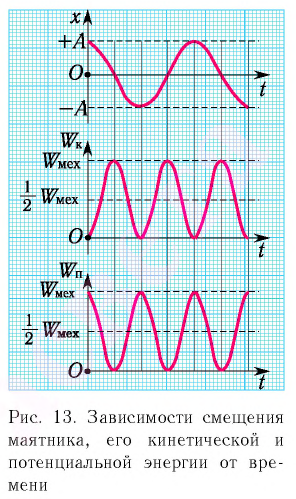
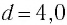 см и при прохождении положения равновесия достигает скорости, модуль которой
см и при прохождении положения равновесия достигает скорости, модуль которой 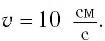 Определите период
Определите период 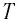 колебании маятника.
колебании маятника. 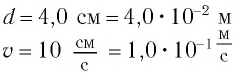
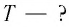
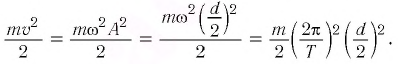
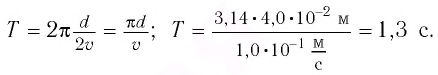
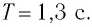
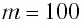 г находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью
г находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью 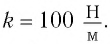 Его смешают на расстояние
Его смешают на расстояние 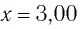 см от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой
см от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой 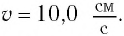 Определите потенциальную
Определите потенциальную 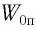 и кинетическую
и кинетическую 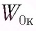 энергию груза в начальный момент времени. Запишите кинематический закон движения груза.
энергию груза в начальный момент времени. Запишите кинематический закон движения груза.
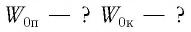
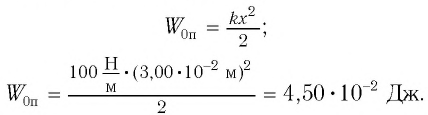
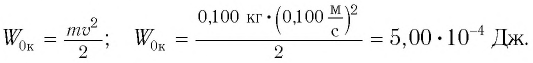
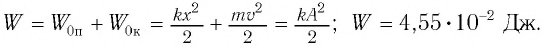
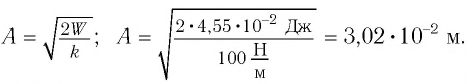
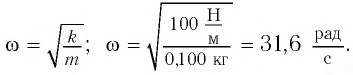
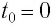 координата груза
координата груза 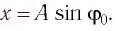 Отсюда начальная фаза:
Отсюда начальная фаза: