Будем рассматривать однородное линейное уравнение второго порядка
Ly ≡ a2(x)y» + a1(x)y’ + a0(x)y = 0. Его можно записать по-другому:
 | (15) |
Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х0) = уo, y'(xo) = y1, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида
 | (16) |
где α1, α2, β1, β2, A, B — заданные числа, причем по крайней мере одно из чисел α1, α2, и одно из чисел β1, β2, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).
Наряду с уравнением (15) рассмотрим уравнение
 | (17) |
содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.
Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде
<Lλy = 0, l1y = 0, l2y = 0>.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид
| y» + λy = 0. | (18) |
Из множества краевых условий вида (16) ограничимся тремя частными случаями:
1) краевые условия первого рода
| y(a) = y(b) = 0, | (19) |
2) краевые условия второго рода
| y'(a) = y'(b) = 0, | (20) |
3) краевые условия третьего рода
 | (21) |
Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.
Видео:Ягола А. Г. - Интегральные уравнения - Задача Штурма-Лиувилля. Теорема СтекловаСкачать

Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.
Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.
Доказательство. Напомним, что определителем Вронского функций у = y1(x) и у = у2(x) называется определитель вида
Рассмотрим однородные краевые условия общего вида (16). Пусть у1(x) и у2(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства
Числа α1, и α2 не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:
Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.
Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.
Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.
Видео:Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y1(x) и у2(x) — линейно зависимые функции.
Свойство 2. Две собственные функции у1(x) и у2(x), соответствующие различным собственным значениям λ1 и λ2 (λ1 ≠ λ2), на отрезке [а, b] ортогональны.
Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у1 и у2 и продифференцируем его:
Так как у1 и у2 — решения уравнения (18) при λ = λ1 и λ = λ2, соответственно, то получим
Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь


Функции y1(x) 0 и у2(х) 0, поэтому 
Значит, y1(x) и у2(х) на отрезке [а, b] ортогональны.
Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y1(x) и у2(х) ортогональны на отрезке [а, b] с весом r(x), если
Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:
Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.
Видео:Разбор решения задачи Штурма-ЛиувилляСкачать

Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).
Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.
Доказательство. Предположим, что задача Штурма-Лиувилля <Lλy = 0, l1y = 0, l2y = 0> имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то
Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае
Значит число 


Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.
Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля <Lλ y = 0, l1 y = 0, l2 y = 0> имеет бесконечное число собственных значений λ 1, λ2, . λn, . Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам
Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l1f = 0 и l2f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям yn(х) задачи Штурма-Лиувилля <Lλ y = 0, l1 y = 0, l2 y = 0> :
где коэффициенты Фурье Сn вычисляются по формулам:
Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Эта теорема применяется при решении уравнений математической физики методом Фурье.
Решение задач Штурма-Лиувилля
Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится.
Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r1 = k, r2 = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C1e kx + C2e -kx . Подставим краевые условия в общее решение и получим

Следовательно, система имеет только нулевое (тривиальное) решение C1 = C2 = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r1 = ki и r2 = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C1cos kx + C2sin kx. Подставим краевые условия в общее решение:
 | (22) |
Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть 


Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:
По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:
 | (23) |
и
 | (24) |
Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C1cos kx +C2sin kx, где 
а) для задачи (23)
Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, 


Собственные функции задачи (23) имеют вид 
 |
Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода
| y» + λy = 0, y'(0) = y'(l) = 0. | (25) |
Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C1cos kx + C2sin kx, 
Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или 



Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда
| y» + λy = 0, y'(0) = y(0), y'(l) = 0. | (26) |
При 

Видео:5.1 Задача Штурма-ЛиувилляСкачать


 | (27) |
Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда
coskl — ksinkl = 0 или
| ctgkl = k | (28) |
Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через rn, n = 1,2, . . Тогда 

Рис.13
Численными методами можно найти приближенные значения rn. Из системы (27) при k = rn получим C1n = rnC2n , где C2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид
Они являются собственными функциями краевой задачи (26) с собственными значениями
Уравнение штурма лиувилля решение примеры
        Требуется найти значения параметра     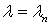
        При этом значения     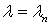
        Характеристическое уравнение исходного дифференциального уравнения
имеет мнимые корни 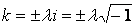
        Следовательно, общее решение исходного дифференциального уравнения
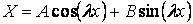
        Подставляем в первое граничное условие
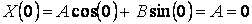
        Получаем
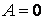

        Подставляем во второе граничное условие
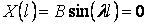
Если принять     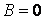

        Поэтому     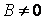
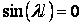
Видео:Решение задачи Штурма-ЛиувилляСкачать

        Отсюда находим собственные значения задачи Штурма-Лиувилля:
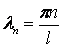
        Тогда собственные функции задачи Штурма-Лиувилля
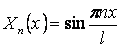
📺 Видео
Дифференциальные уравнения | задача Штурма - Лиувилля | формулировкаСкачать

Дифференциальные уравнения | задача Штурма - Лиувилля | мотивацияСкачать

УМФ решение краевой задачи уравнения колебания струны. Метод Фурье. Задача Штурма–Лиувилля. Пример.Скачать

Колыбасова В.В. - Методы математической физики. Семинары - 2. Задача Штурма-ЛиувилляСкачать

Боголюбов А. Н. - Методы математической физики - Задача Штурма-ЛиувилляСкачать

Колыбасова В.В. - Методы математической физики. Семинары - 8. Задача Штурма-Лиувилля в пол. коорд. 1Скачать

Разностная задача на собственные значения. Задача Штурма-Лиувилля. Численные методы. Лекция 12Скачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Методы математической физики. Задача Штурма-Лиувилля, Метод Фурье. Фролова Е.В.Скачать

Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 2Скачать

Горицкий А. Ю. - Уравнения математической физики - Задача Штурма-ЛиувилляСкачать

Волков В.Т. - Интегральные уравнения и вариационное исчисление - 4. Задача Штурма-ЛиувилляСкачать

Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 3Скачать