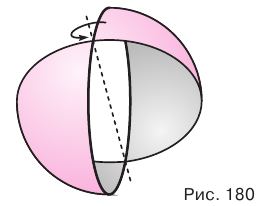
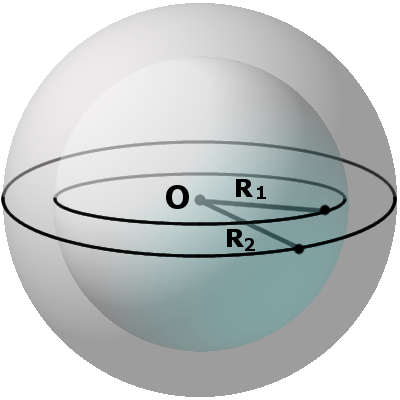
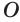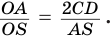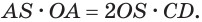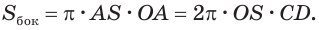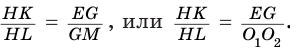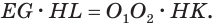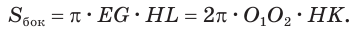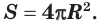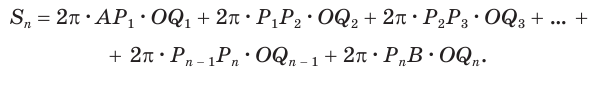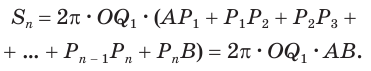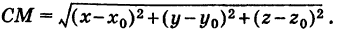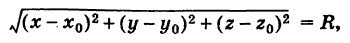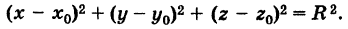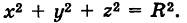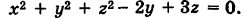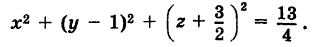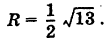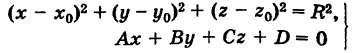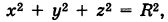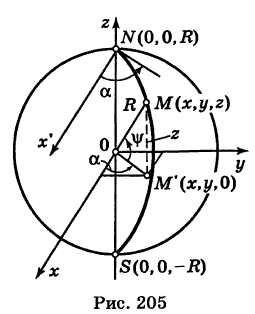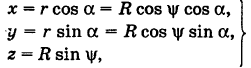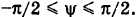Сферой называется поверхность, полученная вращением окружности вокруг какого-либо ее диаметра (рис. 180). Центр этой окружности называется центром сферы.
Отрезок, соединяющий центр сферы с любой ее точкой, называется радиусом сферы, отрезок, соединяющий две точки сферы, — хордой сферы, а хорда, которой принадлежит центр сферы, — диаметром сферы (рис. 181).
Из определения сферы следует, что все ее точки равноудалены от центра сферы. Поэтому все радиусы сферы равны друг другу.
- Теоремы
- Уравнение сферы
- Конспект занятия по теме «Уравнение окружности и сферы» (1 курс СПО)
- Сфера, шар, сегмент и сектор. Формулы и свойства сферы
- Уравнение сферы
- Основные свойства сферы и шара
- Секущая, хорда, секущая плоскость сферы и их свойства
- Касательная, касательная плоскость к сфере и их свойства
- 🎦 Видео
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Теоремы
Теорема 1.
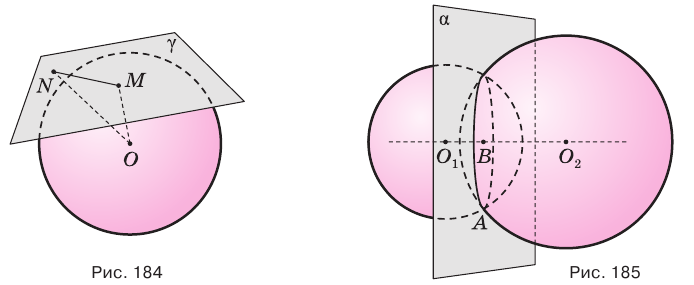
Сечение сферы плоскостью есть окружность, центр которой совпадает с основанием перпендикуляра, опущенного из центра сферы на секущую плоскость.
Доказательство:
Пусть сфера с центром
Пусть 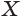
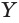
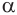
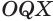
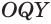
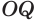
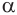
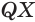
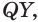
Отрезок 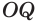
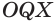
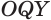
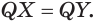
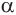


Следствие. Радиус 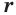
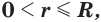
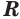
Сечение имеет наибольший радиус 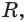
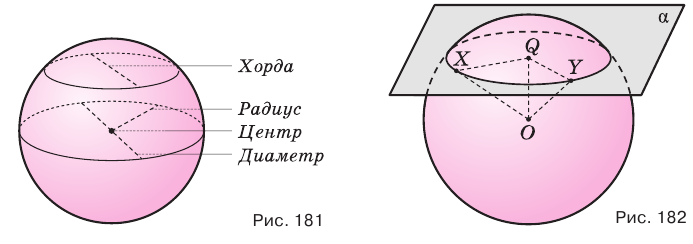
Плоскость, имеющая со сферой единственную общую точку, называется касательной плоскостью сферы. Общая точка сферы и касательной плоскости называется точкой касания.
Прямая касательной плоскости сферы, проходящая через точку касания, имеет со сферой единственную общую точку. Такая прямая называется касательной прямой сферы.
Теорема 2.
Касательная плоскость сферы перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
Пусть плоскость 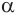
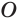

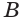
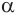

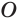

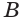
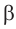
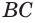

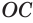
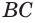
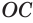
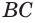

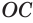
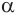
Теорема 3.
Если плоскость проходит через точку сферы и перпендикулярна радиусу, проведенному в эту точку, то она является касательной плоскостью сферы.
Доказательство:
Пусть плоскость 

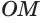
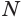


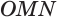
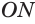
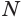





Теоремы 2 и 3 выражают соответственно свойство и признак касательной плоскости сферы.
Теорема 4.
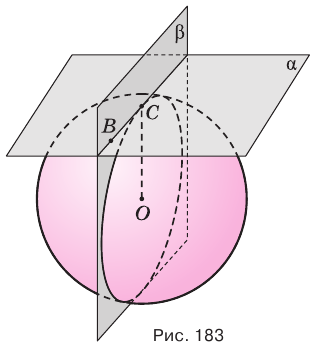
Две сферы пересекаются по окружности, плоскость которой перпендикулярна прямой, проходящей через центры сфер.
Доказательство:
Пусть имеются две пересекающиеся сферы с центрами 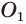
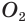
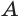
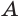
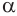
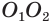
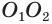

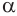


Других общих точек данные окружности не имеют. Допустим, что это не так. Пусть 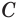

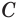
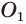
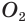
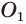
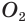

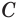
Но это противоречит утверждению о том, что две окружности имеют не более двух общих точек.
Прежде чем доказывать утверждение о поверхности сферы, обобщим утверждения о боковых поверхностях конуса, усеченного конуса и цилиндра.
Теорема 5.
Боковая поверхность конуса, усеченного конуса, цилиндра равна боковой поверхности цилиндра с той же высотой и радиусом основания, равным длине перпендикуляра, соединяющего середину образующей с точкой на оси этого тела.
Доказательство:
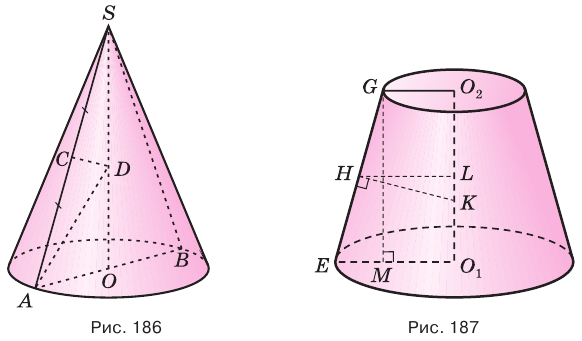
Пусть есть конус с вершиной 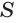
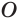
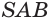
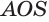
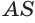
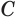
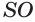
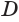
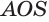
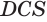
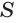
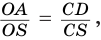
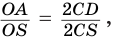
Отсюда
С учетом этого для боковой поверхности 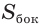
Пусть есть усеченный конус, полученный вращением прямоугольной трапеции 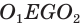
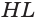
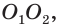
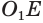
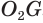
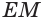
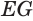
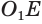
В плоскости 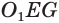
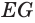
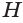
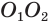
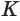
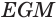
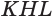
Отсюда
С учетом этого для боковой поверхности 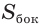
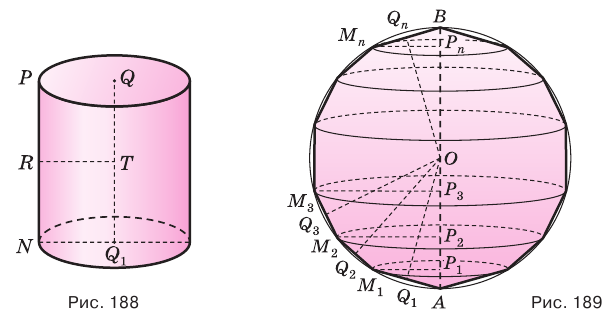
Для цилиндра утверждение очевидно (рис. 188).
Теорема 6.
Поверхность сферы равна учетверенной площади большого круга:
Доказательство:
Пусть есть сфера, образованная вращением полуокружности 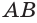
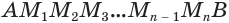
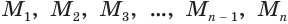
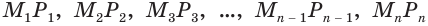
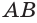


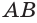
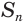
Учтем, что отрезки 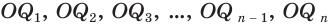
Пусть радиус сферы равен 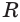
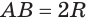
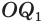
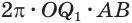
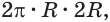
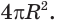
Учитывая, что 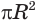
Видео:№577. Напишите уравнение сферы с центром А, проходящей через точку N, если: а) А ( — 2; 2; 0)Скачать

Уравнение сферы
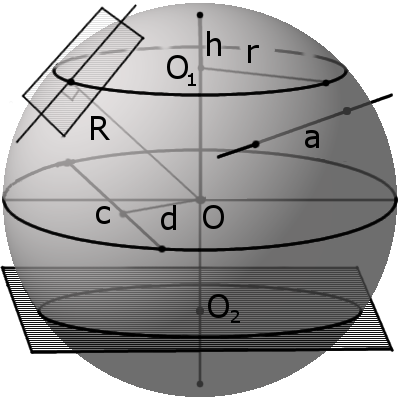
Определение: Сферой радиуса R называется множество всех точек пространства, расстояние от каждой из которых до данной точки (центра) равно R.
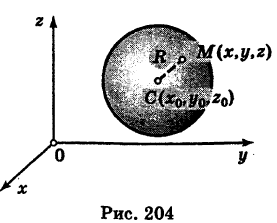
Выведем уравнение сферы. Пусть 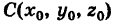
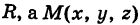
Приравнивая это выражение R, получим уравнение сферы
Если центр сферы совпадает с началом координат, то х0 = 0, у0 = 0, 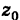
Пример:
Определить координаты центра и радиус сферы
Решение:
Объединяя члены, содержащие одноименные текущие координаты, и дополняя их до полных квадратов, будем иметь
Следовательно, центр сферы находится в точке 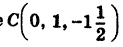
Заметим, что совокупность
уравнений сферы и плоскости определяет окружность, по которой пересекаются плоскость и сфера (если это множество не пусто). В частности, если 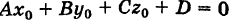
Уравнение окружности можно также писать в параметрическом виде.
Пример:
Написать параметрические уравнения меридиана сферы
проходящего через полюсы 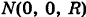
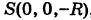
Решение:
За параметр текущей точки 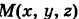
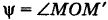
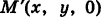
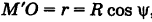
где
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники
- Окружность
- Призма в геометрии
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Конспект занятия по теме «Уравнение окружности и сферы» (1 курс СПО)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Занятие № 88. Уравнение окружности и сферы.
Окружностью называется множество всех точек плоскости, равноудаленных от данной точки этой плоскости, называемой центром.
Уравнение окружности с центром в точке О( a ; b ) и радиусом r имеет вид 
Пример. Составить уравнение окружности с центром в точке (5; -7) и проходящей через точку (2; -3).
Решение. Найдем радиус окружности как расстояние от центра до данной ее точки: 

1. Составьте уравнение окружности: 1) с центром в точке (-1; 4) и проходящей через точку (3; 5); 2) с центром в точке (-3; 0) и проходящей через точку (2; 4).
2. Составьте уравнение окружности, проходящей через начало координат и имеющей центр в точке: 1) (-2; 3); 2) (3; -5).
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки – центра сферы. Данное расстояние называется радиусом сферы.
Любой отрезок, соединяющий центр сферы и какую-нибудь точку сферы, также называют радиусом сферы. Отрезок, соединяющий две точки сферы, называется диаметром сферы. Тело, ограниченное сферой, называется шаром.
Выведем уравнение сферы радиуса R с центром C ( x 0 ; y 0 ; z 0 ) . Расстояние от произвольной точки М( x ; y ; z ) до точки С вычисляется по формуле 
Если точка М лежит на данной сфере, то МС= R , или МС 2 = R 2 , то есть координаты точки М удовлетворяют уравнению 
Если же точка М( x ; y ; z ) не лежит на данной сфере, то МС 2 ¹ R 2 , то есть координаты точки М не удовлетворяют уравнению. Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром C ( x 0 ; y 0 ; z 0 ) имеет вид 
Пример. Напишите уравнение сферы с центром А, проходящей через точку N , если А(0; 0; 0), N (5; 3; 1).
Решение. Уравнение сферы имеет вид 


Следовательно, уравнение сферы: 

1. Напишите уравнение сферы радиуса R с центром А, если: а) А(2; -4; 7), R =3; б) А(0; 0; 0), 
2. Напишите уравнение сферы с центром А, проходящей через точку N , если:
Видео:11 класс, 20 урок, Уравнение сферыСкачать

Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Формула. Объём шара:
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
Видео:Уравнение окружности (1)Скачать

Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2
Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Основные свойства сферы и шара
Видео:№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Секущая, хорда, секущая плоскость сферы и их свойства
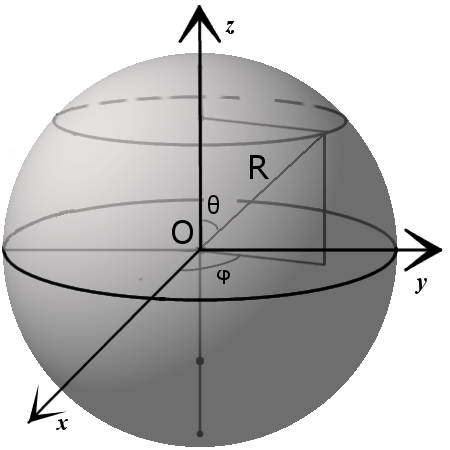
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Касательная, касательная плоскость к сфере и их свойства
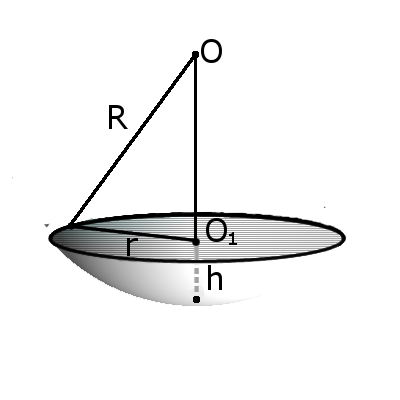
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h 2 π | (3R — h ) |
| 3 |
S = π R(2 h + √ 2 h R — h 2 )
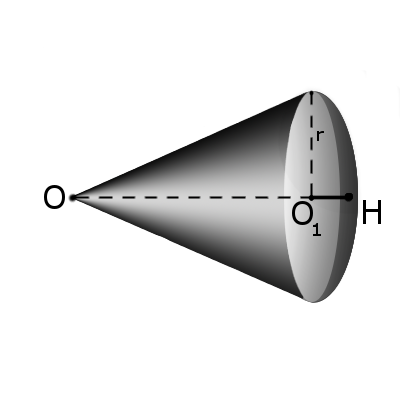
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2 π R 2 h |
| 3 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
🎦 Видео
Геометрия. 10 класс. Уравнение сферы /16.03.2021/Скачать

начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

Уравнение окружностиСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать