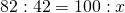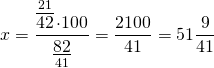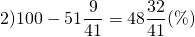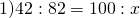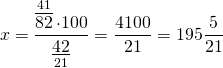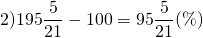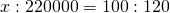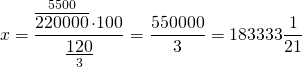О чем эта статья:
- Основные определения
- Типы задач на проценты
- Тип 1. Нахождение процента от числа
- Тип 2. Нахождение числа по его проценту
- Тип 3. Нахождение процентного отношения двух чисел
- Тип 4. Увеличение числа на процент
- Тип 5. Уменьшение числа на процент
- Тип 6. Задачи на простые проценты
- Тип 7. Задачи на сложные проценты
- Задачи на проценты с решением
- Как решать задачи на проценты в 6 классе
- 40 Comments
- Презентация по математике на тему «Решение задач на проценты с помощью уравнений» (6 класс)
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- 📺 Видео
Видео:Как решать задачи на ПРОЦЕНТЫ �Скачать

Основные определения
Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.
Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».
Процент — это одна сотая часть от любого числа. Обозначается вот так: %.
Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:
Видео:Решение задач на проценты способом пропорции. 6 класс.Скачать

Типы задач на проценты
В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.
Тип 1. Нахождение процента от числа
Чтобы найти процент от числа, нужно число умножить на процент.
Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?
Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).
Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.
Тип 2. Нахождение числа по его проценту
Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.
Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.
Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?
Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.
40 : 0,16 = 40 · 100 : 16 = 250
Ответ: 250 задач собрано в этом учебнике.
Тип 3. Нахождение процентного отношения двух чисел
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.
Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?
Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.
10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%
Ответ: в классе 40% девочек.
Тип 4. Увеличение числа на процент
Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.
А можно воспользоваться формулой:
a = b · (1 + с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?
Как решаем: можно найти 12% от 110:
Прибавить к исходному числу:
110 + 13,2 = 123,2 рубля.
Или можно воспользоваться формулой, тогда:
110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.
Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.
Тип 5. Уменьшение числа на процент
Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.
А можно воспользоваться формулой:
a = b · (1 − с : 100),
где a — число, которое нужно найти,
b — первоначальное значение,
c — проценты.
Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?
Как решаем: можно найти 25% от 100:
Вычесть из исходного числа 100 − 25 = 75 человек.
Или можно воспользоваться формулой, тогда:
100 · (1 − 25 : 100) = 75/p>
Ответ: 75 выпускников в этом году.
Тип 6. Задачи на простые проценты
Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.
Формула расчета выглядит так:
S = а · (1 + у · х : 100),
где a — исходная сумма,
S — сумма, которая наращивается,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?
Как решаем: подставим в формулу данные из условий задачи.
70 000 · (1 + 12 · 8 : 100) = 137 200
Ответ: 137 200 рублей вернет Мария через год.
Тип 7. Задачи на сложные проценты
Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.
Формула расчета выглядит так:
S = а · (1 + х : 100) y ,
где S — наращиваемая сумма,
a — исходная,
x — процентная ставка,
y — количество периодов начисления процента.
Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?
Как решаем: просто подставим в формулу данные из условий задачи:
10000 · (1 + 10 : 100)3 = 13 310
Ответ: 13 310 рублей снимет Антон через год.
Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!
Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.
- 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
- 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
- 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
- 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
- 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
|
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Видео:Как быстро решать задачи на процентыСкачать

Задачи на проценты с решением
Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.
Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
Ответ: масса воды 53,2 кг
Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?
Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.
Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:
0,6х — 0,25 * 0,6x = 0,45x
После двух понижений изменение цены составит:
Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.
Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?
По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто
Получается, что стоимость одной пары брюк — это 23% стоимости пальто.
Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.
Ответ: пять пар брюк на 15% дороже, чем одно пальто.
Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.
По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.
Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.
Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.
А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.
Ответ: заработок жены составляет 27%.
Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?
Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.
Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.
Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.
Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.
Видео:Математика 6 класс (Урок№9 - Понятие о проценте.)Скачать

Как решать задачи на проценты в 6 классе
Предлагаю вашему вниманию легкий способ разобраться, как решать задачи на проценты в 6 классе.
При решении задачи на проценты первым делом нужно определить вид задачи. Задачи на проценты в 6 классе можно подразделить на три вида:
Определить вид задачи на проценты можно по записи ее условия. Если напротив 100% стоит число, то это — задача на нахождение процентов от числа. Если число напротив 100% неизвестно, то это — задача на нахождение числа по его процентам. Если же неизвестное значение стоит в колонке процентов, то это — задача на нахождение процентного отношения двух чисел.
Рассмотрим на примерах, как научиться определять вид задачи на проценты.
1. Из картофеля выходит 20% крахмала. Сколько крахмала выйдет из 45 т картофеля?
| тонны | % | |
| Картофель | 45т | 100% |
| Крахмал | ? | 20% |
Это задача на нахождение процентов от числа (так как напротив 100% стоит число).
2. Руда содержит 67% железа. Сколько нужно руды для получения 13,4 т железа?
| тонны | % | |
| Руда | ? | 100% |
| Железо | 13,4т | 67% |
Это задача на нахождение числа по его процентам (так как напротив 100% стоит ?)
3. Из 400 зерен пшеницы взошло 360. Определить процент всхожести семян.
| Зерна | % | |
| Всего посеяли | 400 | 100% |
| Взошло | 360 | ? |
Это задача на процентное отношение (так как в колонке процентов стоит ?).
Видео:Математика 6 класс (Урок№11 - Задачи на проценты. Часть 1.)Скачать

40 Comments
Спасибо, вы очень помогли) Хороший сайт, интересный подход к задачам…только…не было бы этих пошлых реклам =
Уважаемый (ая) ххх! Работа над сайтом требует много сил и времени. Кроме того, нужно оплачивать хостинг и доменное имя. Поэтому хорошо, когда реклама есть.
Здравствуйте ваш сайт меня спасает , 🙂 у вас есть задачи на 8 — 9 классы ?
огромное вам спасибо мне завтра cдавать экзамены для поступления в кадетское училище и сайт очень помог я все вспомнил что мы проходили в школе
Саша, желаю Вам успешной сдачи экзаменов!
А расскажите, пожалуйста, простой способ, как можно решить подобную задачу:
Прайс повысился сначала на 7%, а потом еще на 5%. На сколько процентов выросла первоначальная цена?
Или вот еще такое:
УСН составляет 6% Как узнать, на сколько процентов нужно увеличить сумму платежа, чтобы полностью компенсировать эти 6% (если просто прибавить к сумме 6%, то и значение для 6% увеличится, а значит сумма «на руки» тоже получится чуть меньше…).
Мне скоро поступать в финский ВУЗ на бизнес-специальность. Математика была давно. А таких задач в тесте — больше половины 🙂 Вроде, и не сложно. Но я пока не могу сообразить, что к чему.
Самый простой способ (но это на мой взгляд) — первоначальную цену можно обозначить, к примеру, а. Это 100%. После увеличения на 7% цена составила 107% от первоначальной, то есть 1,07а. После увеличения цены еще на 5% получим 1,05∙1,07а=1,1235а. Разница между новой и первоначальной ценой составляет 1,1235а-а=0,1235. Переводим десятичную дробь в проценты: 0,1235=12,35%. Здесь подробнее.
Другую задачу завтра посмотрю. Извините, засыпаю. Еще ошибусь где-либо, дети станут возмущаться: «Как вы смеете других учить, а сами ошибки делаете?» 🙂
Я для себя решил немного по-другому. В задачах о процентах всегда есть первоначальное число — база (Б), результат изменения (Р) и пропорция — коэффициент изменения базы (к).
Одно соотношение: Р=Б*к.
Если база Б уменьшилась на 6%, то к=0,94.
при известном результате (сумма платежа, допустим 100 единиц) — Р, базу находим так:
проверка: если от 106,383 вычесть 6%, получится 100.
Вся беда и путаница в калькуляторах в том, что знак процентов работает только с одним типом задач «нахождение результата при известной базе».
Так мне кажется.
Спасибо огромное Вам, Светлана! Дочь проболела все задачи на проценты. Чтобы ей помочь, обратилась к Вашему сайту. Все так понятно и просто! Успехов Вам и удачи во всем!
Спасибо, Ольга! Желаю здоровья и успехов Вам и дочери!
спасибо завтра а олимпиаду ехать а я забыл темы много болел отличник но забыл по болезням
Игорь, желаю Вам здоровья и отличного результата на олимпиаде!
Здравствуйте Светлана. У меня такая задача сможете помочь с ответом. Гуля весит 42 кг, а Боря 82 кг. Вот вопрос на сколько % Гуля меньше чем Боря . И на скобки % Боря тежелее чем Гуля . У этой задачи 1 ответ должен быть . Или нет .
Гуля, это две разные задачи.
1. Так как нужно найти, на сколько процентов вес Гули меньше веса Бори, то 100% здесь — вес Бори (как уровень для сравнения).
________кг_______%
Боря____82____100
Гуля____42_____х
1) Составляем пропорцию и решаем её:
Значит, вес Гуля составляет 51 9/41 % от веса Бори.
на столько процентов вес Гули меньше веса Бори.
2. Так как требуется найти, на сколько Боря тяжелее, чем Гуля, в качестве 100% здесь берём вес Гули.
________кг_______%
Гуля____42_____100
Боря____82______х
столько процентов составляет вес Бори от веса Гули.
на столько процентов Боря тяжелее Гули.
Помогите пожалуйста решить задачку! Мужчина продал машину за 220000 руб, он заработал на ней 20%. за какую сумму он ее купил?
Первоначальная цена машины составляет 100%. Так как мужчина заработал на продаже 20%, то он продал её за 120% от первоначальной цены.
____________руб___________%
Купил_____х___________100
Продал___220000____120
Составляем пропорцию и решаем её:
За столько рублей мужчина купил машину.
Помогите пожалуйста с задачей!У Алёши 80 марок, у Бори на 20% больше,а у Вовы на 25% меньше. Сколько марок у Вовы и у Бори в отдельности?
20% — это 1/5 часть числа. 80:5=16. Значит, у Бори на 16 марок больше, чем у Алёши, то есть у него 80+16=96 марок.
25% — это 1/4 часть числа. 80:4=20. Следовательно, у Вовы на 20 марок меньше, чем у Алёши, то есть у Вовы 80-20=60 марок.
доброе утро. Сегодня котрольная,не могу решить такую залачу, помогите пожалуйста. Сплав, который используется при паянии, составляет 58% свинца и 2,5% разных примесей. Остальной сплав — олово. Найдите массу куска этого сплава, если в нем свинца на 22,2 г больше, чем олова.
Добрый день, Алёша!
1) 100-(58+2,5)=39,5 (%) сплава составляет олово
2) 58-39,5=18,5 (%) на столько свинца больше, чем олова.
3) 22,2:18,5=1,2 (г) в 1%
4) 1,2∙100=120 (г) масса сплава.
На покраску куба размером 2×2×2 требуется 2 грамма краски сколько краски потребуется на покраску куба размером 6×6×6
В 9 раз больше. Но какое отношение Ваш вопрос имеет к решению задач на проценты в 6 классе?
Последняя задача про краску не дает мне покоя, так как у меня другой ответ. Начинаю в себе сомневаться. Пожалуйста, подтвердите мое решение или опровергните, если не трудно.
2*2*2=8
6*6*6=216
216/8=27 раз
2г*27=54г
Заранее благодарна
Речь идет о площади поверхности куба. Поверхность куба состоит из 6 граней, каждая грань — квадрат со стороной а. Соответственно, площадь поверхности куба вычисляется по формуле S=6a². Для куба с ребром a=2 S=6∙2²=24, для куба с ребром a=6 — S=6∙6²=216. Площадь поверхности увеличилась в 9 раз.
Светлана Михайловна, спасибо большое!. Меня заклинило на объемах, я поняла.Очень Вам благодарна.
Задача про веса Бори и Гули очень помогла разобраться, спасибо большое!
Здравствуйте, Светлана.Решите пожалуйста задачу. Бак автомобиля вмещает 60 л бензина. Сколько литров бензина в баке, если заполнено 55% его объема?
Это задача на нахождение процентов от числа.
1) 55%=0,55
2) 0,55∙60=33(л) бензина в баке.
ПОМОГИТЕ РЕШИТЬ!!
В первый день посадили лес на 38% всей площади,во второй день на 32.8 %,а в третий на оставшихся 7.3га.Чему равна площадь отведенная под посадку леса?
Весь лес — 100%. На третий день посадили 100- (38+32,8)=29,2%. Проще всего решить задачу с помощью пропорции. Примем площадь леса за х:
х:100=7,3:29,2. Отсюда х=7,3∙100:29,2 и х=25.
Если пропорцию ещё не изучали — тогда нахождение числа по его процентам: 1)29,2%=0,292; 2) 7,3:0,292=35 (га).
Спасибо Светлана,вы очень помогли. Я очень отстаю по математике,хотя хорошистка. Здоровья вам)
Спасибо, Вам тоже здоровья и успехов в учёбе!
Светлана Михайловна, здравствуйте, обращаемся с просьбой помочь решить задачу:
Найти два натуральных числа а и в такие, что НОД ( а, в) = 288, а НОК ( а, в) = 11202, и каждое из чисел а и в больше 288. Заранее бланодарны за помощь!
НОК ( а, в) — это наименьшее число, которое делится и на а, и на в. НОК ( а, в) = 11202 = 2∙3∙1867.
НОД ( а, в) — это наибольшее число, на которое делится и а, и в. НОД ( а, в) = 288 = 2⁵∙3².
Таким образом, если разложить числа а и в на простые множители,то и а, и в должны в разложении содержать 2⁵∙3². Их наименьшее общее кратное также должно содержать это произведение. Но 2∙3∙1867 не содержит 2⁵∙3². Значит, задача не имеет решения.
Можно было рассуждать иначе. НОК ( а, в) — число, которое делится и на а, и на в. НОД ( а, в) — число, на которое делится и а, и в. Значит, НОК ( а, в) делится на НОД ( а, в). Но 11202 на 288 не делится.
помогите задача 6 класс со схемой проценты вчера продали 180 кг овощей а сегодня на 20% меньше сколько всего продализа 2 дня
180 кг — 100%
? кг — 80%.
1)80%=0,8
2)0,8∙180=144 (кг) овощей продали сегодня
3)180+144=324 (кг) продали всего.
С помощью пропорции можно также, если уже изучили эту тему.
и задумали число увеличили на 2%и получили 750
Видео:Решение задач на проценты способом пропорции. Практическая часть - решение задачи. 6 класс.Скачать

Презентация по математике на тему «Решение задач на проценты с помощью уравнений» (6 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Решения задач на проценты с помощью уравнений
Цель урока: Вспомнить понятие «процент»; Научиться решать задачи на проценты с помощью уравнений.
Процент? Процент – это сотая часть числа. 1% = = 0,01
Заполни таблицу 0,18 0,24 0,9 1 1,23 18 100 24 100 90 100 100 100 123 100 Проценты Обыкновенная дробь Десятичная дробь 18% 24% 90% 100% 123%
Найти соответствие http://aida.ucoz.ru а) 50% жителей 1) Четверть жителей б) 25% жителей 2) Примерно треть жителей в) 100% жителей 3) Половина жителей г) 33% жителей 4) Все жители
Найти 7% от 200 15% от 60 8% от 30% от X 5 16
5390 780 176 352 92,5 Товар: Скидка: Скидка в рублях: Шуба — 38 500 рублей 14 % Платье – 7 800 рублей 10% Шапка — 2 200 рублей 8 % Спортивный костюм — 3 200 рублей 11 % Кроссовки – 1 850 рублей 5 %
Основные этапы решения задачи 1. Проанализировать условие задачи, составить краткую запись. 2. Обозначить неизвестную величину буквой х. 3. Выразить все неизвестные величины через данные и х. 4. Составить уравнение. 5. Решить уравнение. 6. Найти искомую величину. 7. Проверить результат по смыслу задачи. 8. Записать ответ.
Задача № 1 Костя купил тетрадь, заплатив за неё 16 рублей. Оказалось, что он истратил 40% всех своих денег. Сколько денег было у Кости?
Задача № 2 Три ящика наполнены орехами. Во втором ящике лежит 70% орехов лежащих в первом. В третьем лежит 120% от того, что лежит во втором. Сколько орехов в каждом ящике, если в первом на 80 орехов больше, чем в третьем?
Итог урока Что узнали нового на уроке? Что называется процентом? Как найти 1 % от числа? Как перевести в проценты десятичную дробь? Как перевести десятичную дробь в проценты? Где встречается проценты в жизни?
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 925 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 684 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 309 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Математика 6 класс (Урок№84 - Сложные задачи на проценты.)Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 576 301 материал в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Другие материалы
- 19.04.2017
- 733
- 1
- 19.04.2017
- 1321
- 0
- 19.04.2017
- 1163
- 0
- 19.04.2017
- 2221
- 2
- 19.04.2017
- 2490
- 20
- 19.04.2017
- 722
- 3
- 19.04.2017
- 1689
- 2
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 19.04.2017 3170
- PPTX 784.6 кбайт
- 22 скачивания
- Оцените материал:
Настоящий материал опубликован пользователем Уткин Василий Михайлович. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 14147
- Всего материалов: 16
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Математика 6 класс (Урок№51 - Решение задач с помощью уравнений. Часть 1.)Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Объявлен конкурс дизайн-проектов для школьных пространств
Время чтения: 2 минуты
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
Тринадцатилетняя школьница из Индии разработала приложение против буллинга
Время чтения: 1 минута
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📺 Видео
Задача на проценты - три способа решенияСкачать

Как легко считать проценты #математика #проценты #5класс #примерыСкачать

Виленкин. 6 класс за 100 минут. Математика: теория чисел, дроби, уравненияСкачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Эту задачу каждый решал в 6 классе Ох, уж эти процентыСкачать

Решение задач с помощью уравнений. Видеоурок 29. Математика 6 классСкачать

6 класс, 20 урок, ОтношенияСкачать

Прямо пропорциональная и обратно пропорциональная зависимость. 6 класс.Скачать

Задачи на проценты 5 класс. Как найти процент от числа. Как решать задачи по математике. Часть 25.1Скачать

Урок 42. Основные задачи на проценты (6 класс)Скачать

ПРОЦЕНТЫ 😉 ЧАСТЬ I #егэ #математика #профильныйегэ #shorts #огэСкачать

Метод пропорции ⚖️Скачать