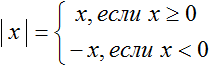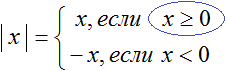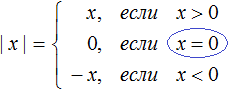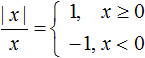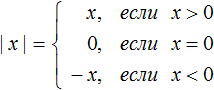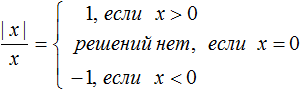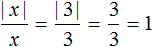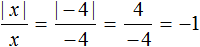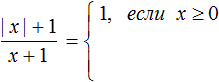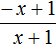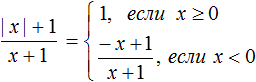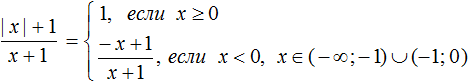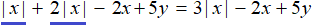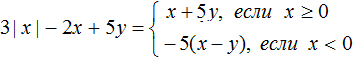В данном уроке мы рассмотрим понятие модуля числа более подробно.
Видео:Уравнения с модулемСкачать

Что такое модуль?
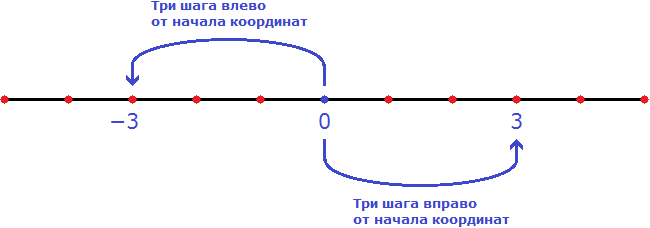
Модуль — это расстояние от начала координат до какого-нибудь числа на координатной прямой. Поскольку расстояние не бывает отрицательным, то и модуль всегда неотрицателен. Так, модуль числа 3 равен 3, как и модуль числа −3 равен 3
Предстáвим, что на координатной прямой расстояние между целыми числами равно одному шагу. Теперь если отметить числа −3 и 3, то расстояние до них от начала координат будет одинаково равно трём шагам:
Модуль это не только расстояние от начала координат до какого-нибудь числа. Модуль это также расстояние между любыми двумя числами на координатной прямой. Такое расстояние выражается в виде разности между этими числами, заключенной под знак модуля:
Где x1 и x2 — числа на координатной прямой.
Например, отметим на координатной прямой числа 2 и 5.
Расстояние между числами 2 и 5 можно записать с помощью модуля. Для этого запишем разность из чисел 2 и 5 и заключим эту разность под знак модуля:
Видим, что расстояние от числа 2 до числа 5 равно трём шагам:
Если расстояние от 2 до 5 равно 3, то и расстояние от 5 до 2 тоже равно 3
То есть, если в выражении |5 − 2| поменять числа местами, то результат не изменится:
Тогда можно записать, что |2 − 5| = |5 − 2|. Вообще, справедливо следующее равенство:
Это равенство можно прочитать так: Расстояние от x1 до x2 равно расстоянию от x2 до x1.
Видео:МодульСкачать

Раскрытие модуля
Когда мы говорим, что |3|= 3 или |−3|= 3 мы выполняем действие называемое раскрытием модуля.
Правило раскрытия модуля выглядит так:
Такую запись мы ранее не использовали. Дело в том, что равенство можно задавать несколькими формулами. Фигурная скобка указывает, что возможны два случая в зависимости от условия. В данном случае условиями являются записи «если x ≥ 0» и «если x .
В зависимости от того что будет подставлено вместо x, выражение |x| будет равно x, если подставленное число больше или равно нулю. А если вместо x подставлено число меньшее нуля, то выражение |x| будет равно −x.
Второй случай на первый взгляд может показаться противоречивым, поскольку запись |x| = −x выглядит будто модуль стал равен отрицательному числу. Следует иметь ввиду, что когда x
Пример 2. Пусть x = 5. То есть мы рассматриваем модуль числа 5
В данном случае выполняется первое условие x ≥ 0, ведь 5 ≥ 0
Поэтому используем первую формулу. А именно | x | = x. Получаем | 5 | = 5.
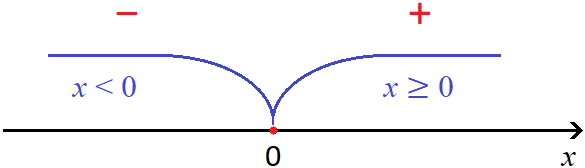
Ноль это своего рода точка перехода, в которой модуль меняет свой порядок раскрытия и далее сохраняет свой знак. Визуально это можно представить так:
На рисунке красные знаки минуса и плюса указывают как будет раскрываться модуль |x| на промежутках x и x ≥ 0 .
К примеру, если взять числа 1, 9 и 13 , а они принадлежат промежутку x ≥ 0, то согласно рисунку модуль |x| раскроется со знаком плюс:
А если возьмём числа, меньшие нуля, например −3, −9, −15, то согласно рисунку модуль раскроется со знаком минус:
Пример 3. Пусть x = √4 − 6. То есть мы рассматриваем модуль выражения √4 − 6,
Корень из числа 4 равен 2. Тогда модуль примет вид
x который был равен √4−6 теперь стал равен −4. В данном случае выполняется второе условие x |√4 − 6| = |2 − 6| = |−4| = −(−4) = 4
На практике обычно рассуждают так:
«Модуль раскрывается со знаком плюс, если подмодульное выражение больше или равно нулю; модуль раскрывается со знаком минус, если подмодульное выражение меньше нуля».
Примеры:
|2| = 2 — модуль раскрылся со знаком плюс, поскольку 2 ≥ 0
|−4| = −(−4) = 4 — модуль раскрылся со знаком минус, поскольку −4 x ≥ 0 расписано подробнее, а именно сказано что если x > 0 , то выражение |x| будет равно x , а если x =0, то выражение |x| будет равно нулю.
Пример 4. Пусть x = 0. То есть мы рассматриваем модуль нуля:
В данном случае выполняется условие x=0, ведь 0 = 0
Пример 5. Раскрыть модуль в выражении |x|+ 3
Если x ≥ 0, то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид x + 3.
Допустим, требуется найти значение выражения |x|+ 3 при x = 5. Поскольку 5 ≥ 0, то модуль, содержащийся в выражении |x|+ 3 раскрóется со знаком плюс и тогда решение примет вид:
Найдём значение выражения |x|+ 3 при x = −6. Поскольку −6 |x| + 3 = 3 − x = 3 − (−6) = 9
Пример 6. Раскрыть модуль в выражении x +|x + 3|
Если x + 3 ≥ 0, то модуль |x + 3| раскроется со знаком плюс и тогда исходное выражение примет вид x + x + 3 , откуда 2x + 3.
Найдём значение выражения x +|x + 3| при x = 4. Поскольку 4 ≥ −3, то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив 4 получим 11
Найдём значение выражения x +|x + 3| при x=−3.
Поскольку −3 ≥ −3 , то согласно нашему решению модуль выражения x +|x + 3| раскрывается со знаком плюс, и тогда исходное выражение принимает вид 2x+3, откуда подставив −3 получим −3
Пример 3. Раскрыть модуль в выражении
Как и прежде используем правило раскрытия модуля:
Но это решение не будет правильным, поскольку в первом случае написано условие x ≥ 0 , которое допускает что при x = 0 знаменатель выражения 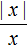
В данном примере удобнее использовать подробную запись правила раскрытия модуля, где отдельно рассматривается случай при котором x = 0
Перепишем решение так:
В первом случае написано условие x > 0 . Тогда выражение 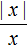
И так будет при любом x , бóльшем нуля.
Во втором случае написано условие x = 0 . Тогда решений не будет, потому что на ноль делить нельзя.
В третьем случае написано условие x . Тогда выражение 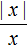
Пример 4. Раскрыть модуль в выражении
Если x ≥ 0 , то модуль, содержащийся в числителе, раскроется со знаком плюс, и тогда исходное выражение примет вид 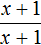
Если x , то модуль раскроется со знаком минус, и тогда исходное выражение примет вид
Но надо учитывать, что при x = − 1 знаменатель выражения 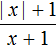
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Преобразование выражений с модулями
Модуль, входящий в выражение, можно рассматривать как полноценный множитель. Его можно сокращать и выносить за скобки. Если модуль входит в многочлен, то его можно сложить с подобным ему модулем.
Как и у обычного буквенного множителя, у модуля есть свой коэффициент. Например, коэффициентом модуля |x| является 1, а коэффициентом модуля −|x| является −1. Коэффициентом модуля 3|x+1| является 3, а коэффициентом модуля −3|x+1| является −3.
Пример 1. Упростить выражение |x| + 2|x| − 2x + 5y и раскрыть модуль в получившемся выражении.
Решение
Выражения|x| и 2|x| являются подобными членами. Слóжим их. Остальное оставим без изменений:
Раскроем модуль в получившемся выражении. Если x ≥ 0, то получим 3x − 2x + 5y , откуда x + 5y .
Если x , то получим − 3x − 2x + 5y , откуда − 5x + 5y . Вынесем за скобки множитель − 5 , получим − 5(x − y)
В итоге имеем следующее решение:
Пример 2. Раскрыть модуль в выражении: −|x|
Решение
В данном случае перед знаком модуля стоит минус. Его можно понимать как минус единицу перед знаком модуля. Если x ≥ 0 , то модуль раскроется со знаком плюс, и тогда исходное выражение примет вид −x
Если x , то модуль раскроется со знаком минус, и тогда исходное выражение примет вид −(−x) откуда получим просто x
Видео:Неравенства с модулем | Математика | TutorOnlineСкачать

Модули. Применение геометрического смысла модуля при решений уравнений и неравенств
Классы: 9 , 10 , 11
Ключевые слова: модуль числа , свойства модуля , геометрический смысл модуля
Цель: Актуализировать знания школьников о смысле понятия «модуль». Учить их применять эти знания при решении уравнении, неравенств и систем уравнении с модулями.
Для того, чтобы научиться решать уравнения и неравенства с модулем, необходимо хорошо разобраться с понятием модуля, его геометрическим смыслом и свойствами.
С рассмотрения этого материала мы и начнем наше занятие.
1. Определение: Модулем числа называется само число, если оно неотрицательно, или число противоположное данному, если оно отрицательно.
Следовательно, при любых значениях переменной |а| есть число неотрицательное.
2. Рассмотрим основные свойства модуля, которые используются при решении уравнений и неравенств, содержащих модуль.
Свойства модуля
— Модуль числа есть величина неотрицательная: |а|>0 или равно 0.
— Модули противоположенных чисел равны: |а|= |-а|
— Модуль произведения равен произведению модулей множителей: |а*в|= |а|*|в|.
— Модуль частного равен частному модулей числителя и знаменателя: |а/в|=|а|/|в|, где в не равен нулю.
— Квадрат модуля равен квадрату подмодульного выражения: |а| 2 =а 2 .
— Модуль суммы не больше суммы модулей ее слагаемых: |а+в|≤|а|+|в|.
При этом равенство |а+в|=|а|+|в| имеет место тогда и только тогда, когда слагаемые одного знака или одно из слагаемых равно нулю.
— Два числа, модули которых равны, либо равны между собой, либо отличаются только знаками, то есть являются противоположными: |а|=|в|, если, а=в или, а=–в.
Преобразование выражений, содержащих модули
При решении уравнении и неравенств с модулем, часто приходится преобразовывать их, раскрывая знак модуля.
Рассмотрим, по каким правилам раскрывается модуль.
Из определения модуля следует: чтобы раскрыть знак модуля, надо знать знак подмодульного выражения.
Составим схему раскрытия модуля:
а) если знак подмодульного выражения неотрицателен, то знак модуля опускается: |а| =а.
б) если знак подмодульного выражения отрицателен, то подмодульное выражение умножается на (-1), то есть заменяется противоположенным выражением: |а| =-1а.
Рассмотрим несколько примеров.
Пример 1.1
а) т.к. с 0, то -7х 5;
б) |3+х|, если х 5, то х-2 > 0, поэтому |х-2|=х-2;
в) т.к. х 0, |8-х|= 8 – х, х-6 (=) 2/3 3х – 2 >(=)0, следовательно, |3[ — 2|= 3х – 2.
4. Задания для самостоятельной работы
б) |- 3/7х|, если х 2 |, если а > 0;
г) |8 + х|, если х > -7;
д) |х — 5| — |х + 4|, если -3 13.
3. Решить неравенство самостоятельно:
4. Решить уравнение:
5. Решить уравнение:
6. Решить неравенство:
7. Найдите наибольшее натуральное значение параметра с при котором решение неравенства
- ||2х + 4| — 7| — 13 ≤ 2с 2 удовлетворяет условию х [-37; 35].
Это задание можно предложить сильным школьникам для домашней работы с последующей проверкой на уроке.
Решения и ответы:
1. Для решения уравнении используем рисунок на доске и правило: «Модуль — это расстояние»:
2. Для решения неравенства сделаем ещё два рисунка.
Значение выражения, стоящего под модулем, не должно превышать 2, значит
Значение выражения, стоящего под модулем, должно быть больше, чем 48 единиц, значит:
18 – х ≥ 48 или 18 – х ≤ -48 => х ≤ -30 или х ≥66.
Видео:Модуль числа. Практическая часть. 6 класс.Скачать

Уравнение с модулем упростить выражение
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
Сервис (своего рода программа для классов 5 и 7, 8, 9, 10, 11) позволяет упрощать математические выражения: алгебра (алгебраические выражения), тригонометрических выражений, выражения с корнями и другими степенями, сокращение дробей, также упрощает сложные буквенные выражения,
для упрощение комплексных выражений вам сюда(!)
Важно В выражениях переменные обозначаются ОДНОЙ буквой! Например, a, b, . z
© Контрольная работа РУ — калькуляторы онлайн
Видео:Как решать уравнение с модулем Уравнение с модулями как решать Как раскрыть модуль в уравненииСкачать

Где учитесь?
Для правильного составления решения, укажите:
📺 Видео
Уравнения с модулем. Часть 2 | Математика | TutorOnlineСкачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Уравнения с модулем за 1 минуту. #математикапрофиль2023 #егэ2023 #математика #школа #fypСкачать

УРАВНЕНИЯ С МОДУЛЕМ | метод интерваловСкачать

Модуль в модуле в уравнении. Алгебра 7 класс.Скачать

Упрощение выражения с модулямиСкачать

Уравнения с модулем. Что такое модуль числа. Алгебра 7 класс.Скачать

Задание №1 "Упростить выражение" по теме "Умножение и сложение многочленов и одночленов". Алгебра 7Скачать

МОДУЛЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Модуль выражения при решении уравнений. Алгебра 7 класс.Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

ВПР 6 КЛАСС. Задание с модулем.Скачать

УРАВНЕНИЕ ПО МОДУЛЮ 😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Упрощение выражения с модулями. Алгебра 8 класс.Скачать