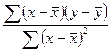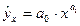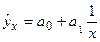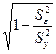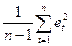Уравнение регрессии имеет вид на сколько изменится в среднем y если x изменится на единицу

4) какая доля вариации результативного признака y учтена в модели и обусловлена влиянием на нее переменной x

Задание № 60

Значение параметра 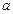в уравнении линейной парной регрессии определяется по формуле:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 61

Уравнение регрессии имеет вид . На сколько единиц своего измерения в среднем изменится при увеличении х на одну единицу своего измерения:

Выберите один из 4 вариантов ответа:

1) увеличится на 2,02

Увеличится на 0,78

3) увеличится на 2,80

Задание № 62

Какой критерий используют для оценки значимости уравнения регрессии:

Выберите один из 4 вариантов ответа:

F — критерий Фишера

2) t — критерий Стьюдента

3) критерий Пирсона

4) d- критерий Дарбина-Уотсона

Задание № 63

Какой коэффициент определяет среднее изменение результативного признака при изменении факторного признака на 1%:

Выберите один из 4 вариантов ответа:

1) коэффициент регрессии

2) коэффициент детерминации

3) коэффициент корреляции

Коэффициент эластичности

Задание № 64

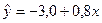
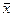
Чему равенсредний коэффициент эластичности, если уравнение регрессии имеет вид , а = 10:

Выберите один из 4 вариантов ответа:

2) 1,6

Задание № 65

Уравнение степенной функции имеет вид:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 66

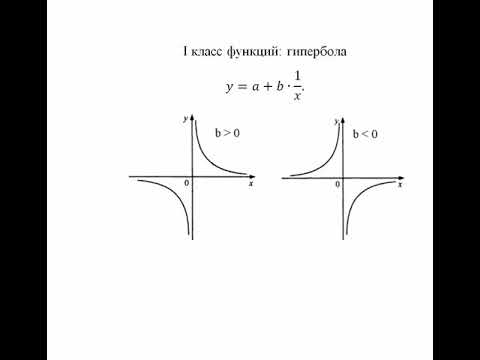
Уравнение гиперболы имеет вид:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 67

Индекс корреляции определяется по формуле:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 68

Несмещенной оценкой дисперсии возмущений в парной регрессии со свободным членом является оценка:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 69

Несмещенной оценкой дисперсии возмущений в парной регрессии без свободного члена является оценка:

Выберите один из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 70

Спецификация парной регрессионной модели может иметь вид:

Выберите несколько из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 71

Выборочное уравнение регрессии между зависимой переменной Y и регрессором X в парной регрессии может иметь вид:

Выберите несколько из 4 вариантов ответа:

1)

2)

3)

4)

Задание № 72

Число степеней свободы t-статистики для проверки значимости оценок параметров модели :

Выберите один из 3 вариантов ответа:

N-2

Задание № 73

Равенство TSS=RSS+ESS для парной регрессии справедливо:

Выберите один из 3 вариантов ответа:

Видео:Коэффициент линейной регрессии, 2 способаСкачать

Корреляция и регрессия

Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.

Для наших данных система уравнений имеет вид:

10a + 356b = 49
356a + 2135b = 9485

Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17

Уравнение регрессии:
y = 68.16 x — 11.17

1. Параметры уравнения регрессии.
Выборочные средние.

1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.

1.2. Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.

1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:

Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.

1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.

Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.

1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим t_крит:
t_крит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если t_набл > t_критич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку t_набл > t_крит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 _r = t 2 _b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:

S 2 _y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
S_y = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S _a — стандартное отклонение случайной величины a.

S_b — стандартное отклонение случайной величины b.

2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bx_p ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X _p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx _i ± ε)
где

С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.

2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H₀ о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H₁ не равно) на уровне значимости α=0.05.
t_крит = (7;0.05) = 1.895

Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).

Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — t_крит S_b; b + t_крит S_b)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — t_a)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.

где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:

где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).

Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.

Обнаружение автокорреляции

1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения e_i с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения e_i (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости e_i от e_i-1.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Контрольные вопросы по эконометрике

Контрольные вопросы по эконометрике.

Каковы основные цели эконометрики?

прогноз экономических и соц-экономических показателей, характеризующих состояние и развитие анализируемой системы. имитация различных возможных сценариев социально-экономического развития

Что понимают под спецификацией модели?

Это построение экономических моделей, т.е. представление экономических моделей в математической форме удобной для проведения эмпирического анализа

Что называется параметризацией?

Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным.

Проверка качества найденных параметров модели и самой модели в целом.

Что означает простая и множественная регрессии?

Простая регрессия представляет собой регрессию между двумя переменными – y и x, т. е. модель вида y=f(x).

Множественная регрессия представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида f=(x1,x2. xk)

Когда предпочтительна парная регрессия?

Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной.

Что понимается под ошибкой спецификации?

Это неправильно выбранная форма модели, недоучет какого-либо существенного фактора в уравнении регрессии, т. е. использование парной регрессии вместо множественной.

Какие основные источники ошибок эконометрических моделей?

Ошибки спецификации, ошибки выборки и ошибки измерения.

Какой вид имеет уравнение парной линейной регрессии?

МНК позволяет получить такие оценки параметров а и b, при которых сумма квадратов отклонений фактических значений от теоретических минимальна:

или.

Какой экономический смысл имеет коэффициент парной линейной регрессии?

Показывает среднее изменение результата с изменением фактора на одну единицу.

Что такое регрессор?

Регрессор – (признак — фактор) – независимая, или объясняющая переменная (х).

Что такое результативный признак?

Результативный признак – зависимая переменная (у)

Какой смысл может иметь свободный член в парной линейной регрессии?

Формально a – значение y при x=0. Если x не имеет и не может иметь нулевого значения, то такая трактовка свободного члена a не имеет смысла. Параметр a может не иметь экономического содержания. Попытки экономически интерпретировать его могут привести к абсурду, особенно при a 0. Интерпретировать можно лишь знак при параметре a. Если a> 0, то относительное изменение результата происходит медленнее, чем изменение фактора.

Чему равен свободный член, если все переменные в линейной модели взяты в отклонениях от средних значений?

Иногда линейное уравнение парной регрессии записывают для отклонений от средних значений: , где , . При этом свободный член равен нулю.

Какова связь между линейным коэффициентом корреляции и коэффициентом парной линейной регрессии?

При линейной регрессии в качестве показателя тесноты связи выступает линейный коэффициент корреляции . Коэффициент регрессии показывает, на сколько единиц в среднем изменится У, когда Х увеличивается на одну единицу. Однако он зависит от единиц измерения переменных. Для исправления Кр. Как показателя тесноты связи нужна такая стандартная система единиц измерения, в которой данные по различным характеристикам оказались бы сравнимы между собой. Эта система использует в качестве единицы измерения переменной её среднее квадратическое отклонение s

Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации как квадрат линейного коэффициента корреляции r2. Он характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:

Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака.

Каково среднее значение случайного отклонения при выполнении предпосылок МНК?

Выполнение предпосылок МНК – условие необходимое для получения несмещенных, состоятельных и эффективных оценок. И при их выполнении среднее значение случайного отклонения равняется нулю.

Что такое гомоскедастичность и гетероскедастичность?

Дисперсия случайных отклонений постоянна: .

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсии отклонений)

Что такое автокорреляция случайных отклонений?

Отсутствие независимости случайных отклонений друг от друга.

Что означает несмещенность оценок параметров уравнения регрессии и их эффективность?

Несмещенность оценки означает, что математическое ожидание остатков равно нулю.

Баланс для сумм квадратов отклонений результативного признака. или Q = Qr + Qe, где Q – общая сумма квадратов отклонений зависимой переменной от средней, Qr и Qe – соответственно, сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтённых факторов.

Что происходит, когда общая СКО равна остаточной?

Когда общая СКО в точности равна остаточной, сумма квадратов, обусловленная регрессией равняется нулю. Фактор х не оказывает влияния на результат, вся дисперсия y обусловлена воздействием прочих факторов, линия регрессии параллельна оси Ох и

В каком случае общая СКО равна факторной?

Общая СКО равна факторной, когда прочие факторы не влияют на результат, y связан с x функционально, и остаточная СКО равна нулю.

Что такое число степеней свободы?

Число степеней свободы (df-degrees of freedom)- это число независимо варьируемых значений признака.

Чему равны числа степеней свободы для различных СКО в парной регрессии?

Для общей СКО требуется (n-1) независимых отклонений, т. к. что позволяет свободно варьировать (n-1) значений, а последнее n-е отклонение определяется из общей суммы, равной нулю. Поэтому

Факторную СКО можно выразить так:

Эта СКО зависит только от одного параметра b,-поскольку выражение под знаком суммы к значениям результативного признака не относится. Следовательно, факторная СКО имеет одну степень свободы, и

Для определения воспользуемся аналогией с балансовым равенством (11). Так же, как и в равенстве (11), можно записать равенство и между числами степеней свободы:

Таким образом, можем записать:

Из этого баланса определяем, что = n–2.

Как определяется статистика по Фишеру?

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза H0:b=0 о том, что коэффициент регрессии равен нулю и следовательно, фактор Х не оказывает влияния на результат У.

Как записываются основная и альтернативная гипотезы при проверке адекватности уравнения регрессии в целом?

, эта гипотеза говорит о том что уравнение регрессии не вносит существенного вклада в объяснение дисперсии зависимой переменой.

Как проверяются гипотезы при использовании статистики по Фишеру в парной регрессии?

Разделив каждую СКО на свое число степеней свободы, получим средний квадрат отклонений, или дисперсию на одну степень свободы:

Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим — критерий для проверки нулевой гипотезы, которая в данном случае записывается как

(18)

Если справедлива, то дисперсии не отличаются друг от друга. Для необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F при разных уровнях существенности и различных числах степеней свободы. Табличное значение F — критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. При нахождении табличного значения F — критерия задается уровень значимости (обычно 0,05 или 0,01) и две степени свободы – числителя (она равна единице) и знаменателя, равная n-2.

Вычисленное значение F признается достоверным (отличным от единицы), если оно больше табличного, т. е. Fфактич>Fтабл(б;1;n-2). В этом случае отклоняется и делается вывод о существенности превышения Dфакт над Dостат., т. е. о существенности статистической связи между y и x.

Если , то вероятность выше заданного уровня (например, 0,05), и эта гипотеза не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи между y и x. Уравнение регрессии считается статистически незначимым, не отклоняется.

Как F — статистика связана с коэффициентом детерминации в парной регрессии?

Величина F-критерия связана с коэффициентом детерминации

Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:

Как рассчитать критерий Стьюдента коэффициента парной линейной регрессии?

Чем больше кривизна линии регрессии, тем больше разница между R2 и r2. Близость этих показателей означает, что усложнять форму уравнения регрессии не следует и можно использовать линейную функцию. Практически, если величина (R2-r2) не превышает 0,1, то линейная зависимость считается оправданной. В противном случае проводится оценка существенности различия показателей детерминации, вычисленных по одним и тем же данным, через t-критерий Стьюдента:

. (56)

Здесь в знаменателе находится ошибка разности (R2-r2), определяемая по формуле:

. (57)

Если , то различия между показателями корреляции существенны и замена нелинейной регрессии линейной нецелесообразна.

33Какая связь между tb — и F – статистиками в парной линейной регрессии?

Существует связь между и :

Отсюда следует, что

33Как построить доверительный интервал для коэффициента парной линейной регрессии?

Доверительный интервал для b определяется как

,

где – рассчитанное (оцененное) по МНК значение коэффициента регрессии,

Стандартная ошибка коэффициента регрессии определяется по формуле:

, (20)

— остаточная дисперсия на одну степень свободы (то же, что и D­остат).

Видео:Регрессия - как строить и интерпретировать. Примеры линейной и множественной регрессии.Скачать

Интервалы прогноза по линейному уравнению регрессии

Чтобы обойти это затруднение, используется так называемое z-преобразование Фишера:

которое дает нормально распределенную величину z, значения которой при изменении r от –1 до +1 изменяются от -∞ до +∞.

В каком месте доверительный интервал прогноза по парной модели является наименьшим?

. (31)

Как видно из формулы, величина достигает минимума при и возрастает по мере удаления от в любом направлении.

Как классический МНК применяется к нелинейным моделям регрессии?

При анализе нелинейных регрессионных зависимостей наиболее важным вопросом применения классического МНК является способ их линеаризации. В случае линеаризации нелинейной зависимости получаем линейное регрессионное уравнение типа (3), параметры которого оцениваются обычным МНК, после чего можно записать исходное нелинейное соотношение.

Несколько особняком в этом смысле стоит полиномиальная модель произвольной степени:

, (34)

к которой обычный МНК можно применять без всякой предварительной линеаризации.

Как преобразуется уравнение гиперболического типа для использования МНК?

Линеаризация уравнения (37) сводится к замене фактора z=1/x, и уравнение регрессии имеет вид (3), в котором вместо фактора х используем фактор z:

Как преобразуется уравнение экспоненциального типа, чтобы использовать МНК?

зависимости показательного (экспоненциального) типа, которые записываются в виде:

(40)

. (41)

Возможна и такая зависимость:

. (42)

В регрессиях типа (40) – (42) применяется один и тот же способ линеаризации – логарифмирование. Уравнение (40) приводится к виду:

. (43)

Замена переменной сводит его к линейному виду:

, (44)

где .

Как преобразуется степенная зависимость при использовании МНК?

Они используются для построения и анализа производственных функций. В функциях вида:

(48)

особенно ценным является то обстоятельство, что параметр b равен коэффициенту эластичности результативного признака по фактору х. Преобразуя (48) путем логарифмирования, получаем линейную регрессию:

, (49)

где .

41Как преобразуется логистическая зависимость для применения МНК?

зависимость логистического типа:

. (52)

Графиком функции (52) является так называемая «кривая насыщения», которая имеет две горизонтальные асимптоты y=0 и y=1/a и точку перегиба , а также точку пересечения с осью ординат y=1/(a+b):

Уравнение (52) приводится к линейному виду заменами переменных .

42Где применяется квадратичная парабола в уравнениях регрессии и при каких условиях?

Такая зависимость целесообразна в случае, если для некоторого интервала значений фактора возрастающая зависимость меняется на убывающую или наоборот. В этом случае можно определить значение фактора, при котором достигается максимальное или минимальное значение результативного признака. Если исходные данные не обнаруживают изменение направленности связи, параметры параболы становятся трудно интерпретируемыми, и форму связи лучше заменить другими нелинейными моделями.

43Какие зависимости используются для кривых Филипса и кривых Энгеля?

Зависимости гиперболического типа имеют вид:

. (37)

Примером такой зависимости является кривая Филлипса, констатирующая обратную зависимость процента прироста заработной платы от уровня безработицы. В этом случае значение параметра b будет больше нуля. Другим примером зависимости (37) являются кривые Энгеля, формулирующие следующую закономерность: с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается, а доля доходов, расходуемых на непродовольственные товары, будет возрастать. В этом случае b 0, то при b 0 . По данным примера , что означает очень тесную зависимость затрат на производство от величины объема выпускаемой продукции.

Величина R находится в границах , и чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии

45В чем особенность вычисления статистики Фишера для полиноминальных регрессии?

Индекс детерминации используется для проверки существенности в целом уравнения нелинейной регрессии по F-критерию Фишера:

, (55)

где n-число наблюдений, m-число параметров при переменных х. Во всех рассмотренных нами случаях, кроме полиномиальной регрессии, m=1, для полиномов (34) m=k, т. е. степени полинома. Величина m характеризует число степеней свободы для факторной СКО, а (n-m-1) – число степеней свободы для остаточной СКО.

Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Уравнение линейной регрессии

Пусть имеется выборка значений пары случайных величин X и Y, которая представлена в виде набора (xiyi), (хг,уг),—, (х,„у„) или в виде табл. 8.2. На основе данных по выборке следует проверить гипотезу о наличии линейной корреляционной зависимости величины Y от величины X, т.е. когда есть основания предполагать, что генеральное уравнение регрессии имеет вид (8.2).

На практике оценкой генерального (истинного) уравнения линейной регрессии (8.2) является выборочное (эмпирическое) сглаживающее уравнение линейной прямой регрессии Y наХ:

где Y_x — имеет смысл оценки условного математического ожидания M(Y/X=x); р_)Х — сглаживающий выборочный коэффициент

линейной регрессии У на X (эмпирическая оценка генерального коэффициента А); b — действительное число (оценка параметра В).

Для оценки параметров сглаживающего выборочного уравнения линейной регрессии Y на X по результатам выборочных наблюдений наиболее употребительным и точным методом является метод наименьших квадратов.

В методе наименьших квадратов требуется, чтобы сумма квадратов разностей S(p_)x,b) наблюдаемых значений у_х от значений Y_x (х,) на линии прямой регрессии оказалась наименьшей:

Необходимым условием экстремума функции нескольких переменных является равенство нулю частных производных по параметрам. Приравнивая к нулю частные производные по параметрам р, 2 находят по формулам

а если исходные данные представлены в виде корреляционной таблицы, то

которые необходимо дополнить выборочной дисперсией случайной величины У

При этом значения величин Х,Х 2 ,У,ХУ в системе уравнений (8.12) находят по формулам (8.8).

Здесь уместно отметить, что выборочные средние квадратичные отклонения о_х, о_у случайных величин X, У равны квадратному корню из выборочной дисперсии и вычисляются соответственно по формулам:

Выборочный слаживающий коэффициент линейной регрессии рух показывает, на сколько единиц в среднем изменится переменная У, при увеличении переменной х на одну единицу, а знак при р_уг указывает направление корреляционной связи между признаками X к Y: при 0-

связь прямая. Геометрически р_у1 является угловым коэффициентом наклона прямой линии Y_x.

Подчеркнем, что регрессия У на X не идентична регрессии X на У, т.е. У, и X_v — различные прямые (рис.8.3, о), которые пересекаются в точке C(X,Y). Первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений по вертикали (рис.8.3, б), а вторая — по горизонтали (рис.8.3, в). Поэтому из уравнения У_х=р_укх+Ь нельзя выразить х через Y_x.

Например, если хотим оценить рост человека по массе, а также решить обратную задачу — сделать вывод о массе человека по росту, то нельзя пользоваться одним и тем же уравнением.

Рис.8.3. Различные виды линий регрессии

Отметим, что по своей форме и существу уравнение (8.5) точно такое же, как и линейная зависимость у=рх+Ь. Разница лишь в том, что у = рх + Ь дает функциональную зависимость величины у от х, а выражение (8.5) — корреляционную зависимость между случайными величинами У и X.

Пример 8.4. Используя условия примера 8.3, составить выборочное уравнение линейной прямой регрессии роста У на объем X грудной клетки мужчин.

Решение. По формулам (8.8) вычислим средние арифметические и остальные значения случайных величин X и У, а по формуле (8.10) выборочную дисперсию:

Используя найденные значения, по формулам (8.7) вычислим параметры

и в соответствии с формулой (8.5) получим искомое выборочное уравнение линейной прямой регрессии роста на объем грудной клетки мужчин

Пример 8.5. Составить выборочное уравнение линейной прямой регрессии У на X и выборочное уравнение линейной обратной регрессии X на У на основании данных табл.8.14.

📽️ Видео

Парная регрессия: линейная зависимостьСкачать

Эконометрика. Линейная парная регрессияСкачать

Эконометрика. Нелинейная регрессия. Степенная функция.Скачать

Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Эконометрика. Оценка значимости уравнения регрессии. Критерий ФишераСкачать

Эконометрика. Множественная регрессия и корреляция.Скачать

Интерпретация коэффициента при логарифмировании в уравнениях регрессииСкачать

Практика Многофакторная регрессияСкачать

МЕТРИКИ РЕГРЕССИИ В МАШИННОМ ОБУЧЕНИИ | MAE, MSE, RMSE, R2, коэффициент детерминации.Скачать

Математика #1 | Корреляция и регрессияСкачать

Множественная регрессия в ExcelСкачать

Линейная регрессияСкачать

Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать

Корреляционно-регрессионный анализ. ЭтапыСкачать

Лекция 8. Линейная регрессияСкачать