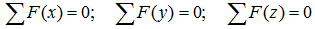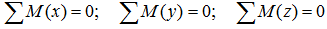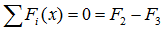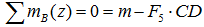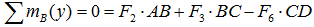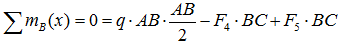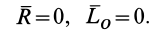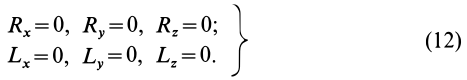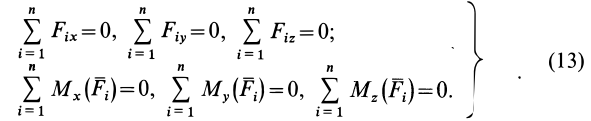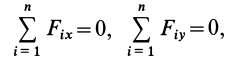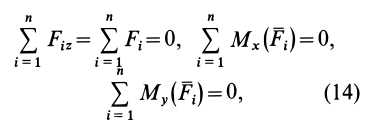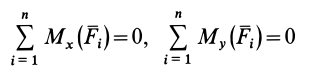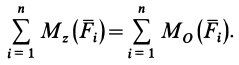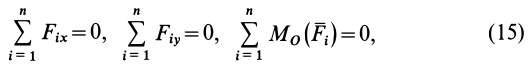Уравнение равновесия моментов относительно точки

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Видео:Определение реакций опор простой рамыСкачать

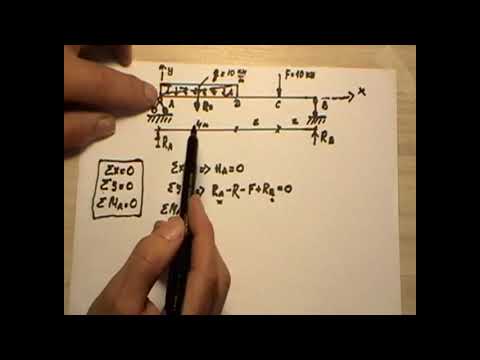
Пример составления уравнений равновесия

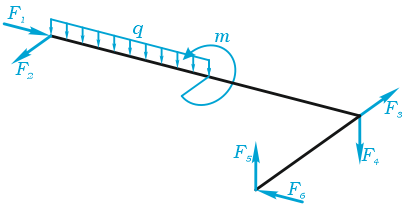
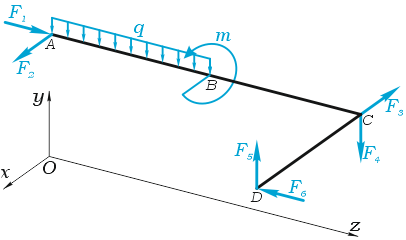
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

• в плоскости xOy:
  
• в плоскости xOz:
  
• в плоскости yOz:
  

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Видео:Момент силы относительно точки и осиСкачать

Условия и уравнения равновесия твердого тела: плоской и пространственной системы сил

Видео:Определение реакций опор в балке. Сопромат.Скачать

Условия равновесия произвольной системы сил

Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:

• либо находится в состоянии покоя;
• либо движется равномерно прямолинейно.

Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:

Тогда обязательное условие равновесия можно записать так:

Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:

где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.

Видео:Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Условия равновесия плоской системы сил

Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:

Вторая форма условий равновесия записывается следующим образом:

Важно! Ось не должна быть перпендикулярна прямой AB.

И, наконец, третья форма условий равновесия выглядит так:

Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.

Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.

Видео:Статика. Условия равновесия плоской системы сил (23)Скачать

Уравнения равновесия для плоской системы сил

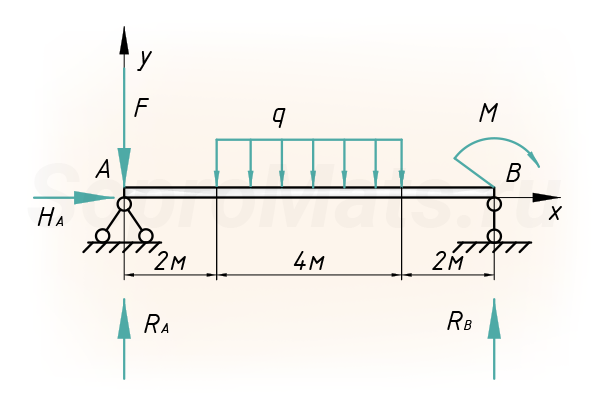
Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:

Сумма моментов относительно точки A:

Сумма проекций всех сил на вертикальную ось (y):

Сумма проекций всех сил на горизонтальную ось(x):

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Условие равновесия пространственной системы сил

Для пространственной системы сил условие равновесие выглядит вот так:

Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Уравнения равновесия для пространственной системы сил

В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:

Видео:Момент силы относительно точкиСкачать

Условия равновесия системы сил в теоретической механике

Содержание:

Условия равновесия системы сил:

Видео:Урок 76. Задачи на правило моментовСкачать

Условия равновесия системы сил в векторной форме

Из теоремы о приведении системы сил к силе и паре сил можно вывести условия равновесия системы сил, действующих на твердое тело. Очевидно, что если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил. Чтобы такая система сил была эквивалентна _ нулю, необходимо и достаточно равенства нулю как силы

Условия (11) являются векторными условиями равновесия для любой системы сил.

Условия равновесия пространственной системы сил в аналитической форме

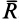
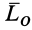
Если при равновесии системы сил, приложенных к твердому телу, главный вектор равен нулю, то его проекция на каждую координатную ось также равна нулю. Это справедливо и для главного момента . Таким образом, из векторных условий равновесия пространственной системы сил следует шесть условий:

Учитывая формулы (5) и (7), эти шесть условий через силы системы выражают в форме

Таким образом, для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

Из общих условий равновесия для произвольной пространственной системы сил получаются условия равновесия для частных систем сил, приложенных к твердому телу.

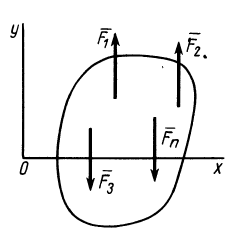
Условия равновесия пространственной системы параллельных сил

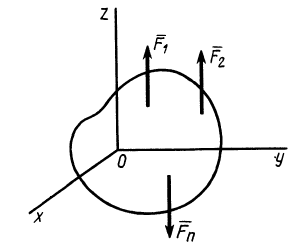
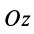
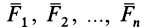
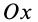
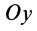
Направим ось параллельно силам (рис. 37). Тогда проекции параллельных сил на перпендикулярные им оси и будут равны нулю и условия

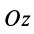
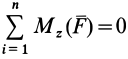
окажутся справедливыми для всех систем параллельных сил, т. е. превратятся в тождества. Момент относительно оси каждой из параллельных сил равен нулю, и условие тоже выполняется для всех систем параллельных сил. Отбрасывая

условия равновесия, которые выполняются тождественно при выбранном направлении оси 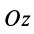, и учитывая, что сумма проекций сил на эту ось является алгебраической суммой сил, из (13) получаем следующие три условия равновесия пространственной системы параллельных сил:

Рис. 37

т. е. для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю.

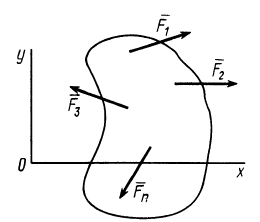
Условия равновесия плоской системы сил

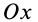
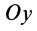
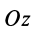
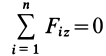
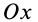
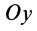
Расположим оси и в плоскости действия сил (рис. 38). Так как ось перпендикулярна силам, то выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат и , и поэтому ее моменты относительно этих осей равны нулю. Таким образом, условия равновесия

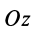
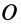
становятся тождествами. Моменты сил относительно оси , перпендикулярной силам, равны алгебраическим моментам этих сил относительно точки . Таким образом,

Из (13) для плоской системы сил после отбрасывания тождеств имеем следующие три условия равновесия:

т. е. для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю.

Рис. 38

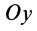
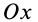
Для плоской системы параллельных сил (рис. 39) одну из осей координат, например , можно выбрать параллельной силам. Тогда сумма проекций параллельных сил на эту ось превратится в алгебраическую сумму сил. Проекция каждой из сил на ось равна нулю; следовательно, сумма проекций сил на ось равна нулю, даже если система сил не находится в равновесии. Это условие выполняется тождественно, и его следует отбросить.

Рис. 39

Итак, для плоской системы параллельных сил из (15) имеем следующие условия равновесия:

т. е. для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю.

Из условий равновесия плоской системы сил (15) можно получить и условия равновесия плоской системы сходящихся сил, для чего за моментную точку надо взять точку пересечения линий действия сходящихся сил. Тогда последнее из условий станет тождеством и в качестве условий равновесия для плоской системы сходящихся сил останутся только два первых условия из (15).

• Плоская система сил
• Трение
• Пространственная система сил
• Центр тяжести
• Система сходящихся сил
• Моменты силы относительно точки и оси
• Теория пар сил
• Приведение системы сил к простейшей системе

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🔥 Видео

Статика. Момент сил. Условия равновесия тел | Физика ЕГЭ, ЦТ, ЦЭ | Физика для школьниковСкачать

Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

§ 5.3. Уравнения равновесия плоской системы силСкачать

Теоретическая механика. Нахождение реакций связей на при плоской системе сил. Задача 1, часть 1Скачать

2.1. Момент силы относительно точки. Момент пары сил (2 из 2)Скачать

Статика. Момент силы относительно точки. Правила и пример вычисления.Скачать

Определение реакций опор простой рамыСкачать

Момент силыСкачать

Произвольная плоская система сил. Задача 1Скачать

Основная теорема статикиСкачать

Определение опорных реакций в простой балке. Урок №1Скачать