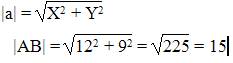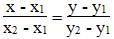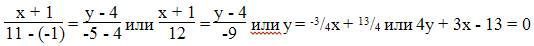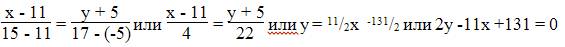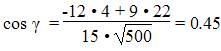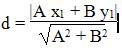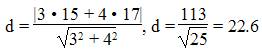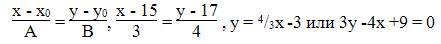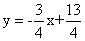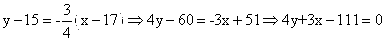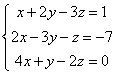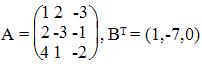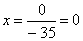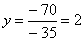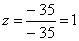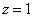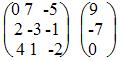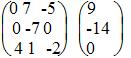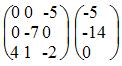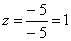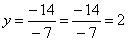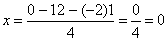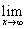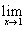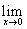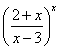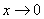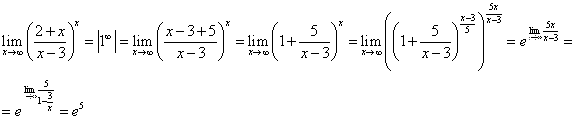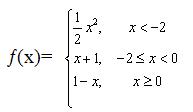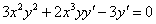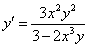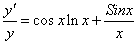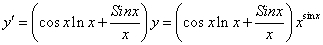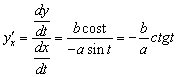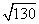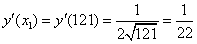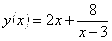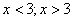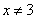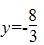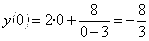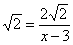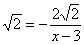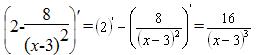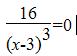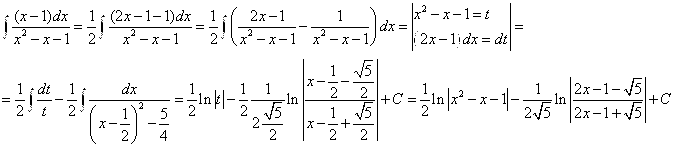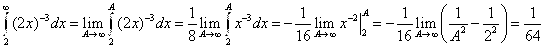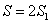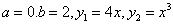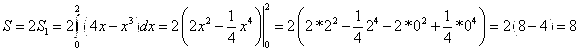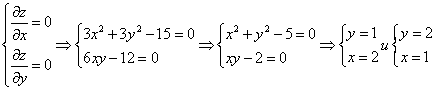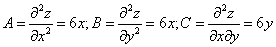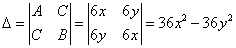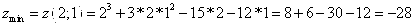Уравнение прямой проходящей через вершину a1 вдоль диагонали параллелепипеда

Видео:№972. Напишите уравнение прямой, проходящей через две данные точки: а) А (1; -1) и В (-3; 2)Скачать

Векторная алгебра и аналитическая геометрия

Векторная алгебра и аналитическая геометрия

1.-10. Векторы a, b, c, d заданы координатами в некотором базисе. Показать, что векторы a, b, c образуют базис в пространстве, и найти координаты вектора d в этом базисе.

11.-20. Даны координаты точек A1, A2, A3, A4. Известно, что отрезки A1A2, A1A3, A1A4 являются смежными ребрами параллелепипеда. Требуется найти:

2) угол между ребрами A1A2 и A1A3 ;

3) площадь грани, содержащей вершины A1,A2,A3 ;

4) объем параллелепипеда;

5) уравнение прямой, проходящей через вершину A1 вдоль диагонали параллелепипеда;

6) уравнение плоскости A1A2A3;

7) угол между ребром A1A4 и гранью, содержащей вершины A1,A2,A3;

8) расстояние от вершины A4 до плоскости A1,A2,A3.

21. Даны уравнения двух сторон параллелограмма: x+2y+1=0 и 2x+y-3=0. Центр параллелограмма находится в точке A(1;2). Найти уравнения двух других сторон. Выполнить чертеж.

22. Даны две вершины треугольника A(2;1), B(4;9) и точка пересечения высот N(3;4). Найти уравнения сторон треугольника. Выполнить чертеж.

23. Даны две противоположные вершины квадрата A(1;3), C(-1;1). Найти координаты двух его других вершин и составить уравнения сторон. Выполнить чертеж.

24. Найти уравнения сторон треугольника, если заданы его вершина A(1;3) и уравнения двух медиан x-2y+1=0, y-1=0. Выполнить чертеж.

25. Известны уравнение одной из сторон квадрата x+3y-3=0 и точка пересечения диагоналей N(-2;0). Найти уравнения остальных ее сторон. Выполнить чертеж.

26. Уравнения боковых сторон равнобедренного треугольника 2x—y+8=0, x-2y-12=0. Точка N(4;0) лежит на основании треугольника. Найти уравнение основания. Выполнить чертеж.

27. Найти уравнения сторон треугольника, зная одну его вершину B(2;-7), а также уравнения высоты 3x+y+11=0 и медианы x+2y+7=0, проведенных из различных вершин. Выполнить чертеж.

28. Точка A(5;-4) является вершиной квадрата, диагональ которого лежит на прямой x-7y-8=0. Написать уравнения сторон и второй диагонали этого квадрата. Выполнить чертеж.

29. Уравнение основания равнобедренного треугольника x+y-1=0, уравнение боковой стороны x-2y-2=0. Точка N(-2;0) лежит на другой боковой стороне. Найти уравнение этой стороны. Выполнить чертеж.

30. Даны уравнения медиан треугольника 5x+4y=0 и 3x—y=0 и одна из его вершин A(-5;2). Найти уравнения сторон треугольника. Выполнить чертеж.

31. Составить уравнение и построить окружность, проходящую через точки A(1;2), B(0;-1) и C(-3;0).

32. Составить уравнение и построить линию, расстояние каждой точки которой от точки A(0;1) в два раза меньше расстояния ее до прямой y-4=0.

33. Составить уравнение и построить линию, сумма квадратов расстояний от каждой точки которой до точек A(-3;0) и B(3;0) равна 50.

34. Составить уравнение и построить линию, расстояние от каждой точки которой до точки A(-1;1) вдвое меньше расстояния до точки B(-4;4).

35. Составить уравнение и построить линию, сумма расстояний от каждой точки которой до точек A(-2;0) и B(2;0) равна .

36. Составить уравнение и построить линию, каждая точка которой находится на одинаковом расстоянии от точки F(2;2) и оси Ox.

37. Составить уравнение и построить линию, расстояния каждой точки которой от точки A(2;0) и прямой 5x+8=0 относятся как 5:4.

38. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки A(5;0) относятся как 2:1.

39. Составить уравнение и построить гиперболу, проходящую через точку N(9;8), если асимптоты гиперболы имеют уравнения y=±(2/3)x.

40. Составить уравнение и построить гиперболу, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса 5x2+8y2=40.

41.-50. Кривая задана уравнением в прямоугольной системе координат. Требуется: 1) найти уравнение кривой в полярной системе координат, полюс которой совмещен с началом прямоугольной системы координат, а полярная ось – с положительной полуосью Ox; 2) построить кривую по точкам со значениями полярного угла φk=kπ/16.

51.-60. Решить систему линейных уравнений методом Гаусса.

51. 52.

53. 54.

55. 56.

57. 58.

4x1+x2+3x3+x4+2x5=7, —x1-x3+7x4+8x5=14,

59. 60.

61.-70. Для данной матрицы A построить обратную матрицу A-1. Выполнить проверку .

71.-80. Определить собственные значения и собственные векторы квадратной матрицы второго порядка.

81.-90. Дано комплексное число z. Требуется:

1) записать число z в алгебраической, тригонометрической и показательной формах;

2) найти все корни уравнения w3+z=0, изобразить эти корни на плоскости комплексной переменной.

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

91.-100. Построить график функции y = f(x) посредством преобразования графика некоторой простейшей элементарной функции.

93. . 94. f(x) = 9x2 – 6x + 3.

99. 100. f(x) = (3x2 – 5x + 2)/(2x2 + x – 3).

101.-110. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.

101. а) б)

в) г)

102. а) б)

в) г)

103. а) б)

в) г)

104. а) б)

в) г)

105. а) б)

в) г)

106. а) б)

в) г)

107. а) б)

в) г)

108. а) б)

в) ; г)

109. а) б)

в) г)

110. а) б)

в) г)

111.-120. Исследовать на непрерывность функцию y = f(x), найти точки разрыва и определить их род. Построить схематический график функции.

111. 112.

113. 114.

(2x2 + 3) /5 при xÎ(- ¥, 1];

115. 116. 6 – 5x при x Î (1, 3);

117. arctg . 118. x∙ctgx.

119. . 120 .

ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

И ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ

121.-130. Найти производную функции одной переменной, исходя из определения производной.

125. y = ctg(3x — 2) . 126.

127. 128.

131.-140. Найти производные первого порядка данных функций, используя правила вычисления производных.

130. 1) ; 2) y = x1/2 / sinx ;

131. 1) y = ln(tg(3x + 2)); 2) ;

3) y = log2(2x + 1); 4) .

133. 1) ; 2) y = ex–y ;

139. 1) ;y = x –sin2x ;

141.-160. Построить график функции, используя общую схему исследования функции.

155. 156. y = ln(16 – x2).

159. y = (2 + x)exp(x — x2). 160

161.-170. Составить уравнение касательной и нормали:

1) к графику кривой y = f(x) в точке, абсцисса которой равна x0;

2) к графику кривой x = x(t), y = y(t) в точке, для которой параметр t равен t0.

Построить графики кривых, касательных и нормалей. Для каждой кривой найти кривизну в указанных точках.

161.

162.

163.

164.

165.

166.

167.

168.

169.

170.

ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

1) вычислить значение u1 функции в точке В;

2) вычислить приближенное значение u1 функции в точке В, исходя из значения u0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом, и оценить в процентах относительную погрешность, возникающую при замене приращения функции ее дифференциалом;

3) составить уравнение касательной плоскости к поверхности f(x,y,z)=C в точке А.

181.-190. Найти наименьшее и наибольшее значения функции

z = f(x; y) в области D, заданной системой неравенств. Выполнить чертеж области D.

1) составить уравнение линии уровня u = C и построить эту линию;

2) в точке А найти градиент и производную по направлению вектора АВ;

3) в точке А построить касательную и нормаль к линии уровня, получив их уравнения.

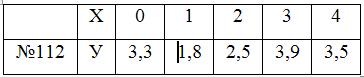
201.-210. Значения функции, полученные экспериментально, приведены в таблице. Методом наименьших квадратов найти наилучшую линейную аппроксимацию экспериментальной зависимости. На плоскости (x,y) построить полученную прямую и точки, заданные табл.1.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Элементы линейной алгебры и аналитической геометрии, графики, матрицы, пределы, мнк

Элементы линейной алгебры и аналитической геометрии

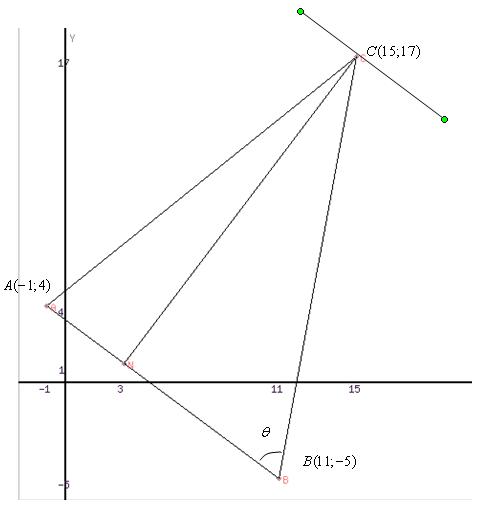
Задания 1-10. Даны координаты точек: А(х1;у1), В(х2;у2), С(х3;у3).

Значения координат точек приведены в таблице к этому заданию.

А) длину отрезка АВ;

Б) уравнение прямых АВ и ВС, проведенных через точки А, В и В, С соответственно;

В) угол θ между прямыми АВ и ВС;

Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;

Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;

Е) построить чертеж, на котором показать заданные точки, угол θ и прямые.

Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi

Здесь X, Y координаты вектора; xi, yi — координаты точки Аi; xj, yj — координаты точки Аj

Для вектора AB X = x2 — x1; Y = y2 — y1

X = 11—1 = 12; Y = -5-4 = -9

А) длина отрезка АВ

Длина вектора a(X;Y) выражается через его координаты формулой:

Б) Уравнение прямой

Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:

Уравнение прямой AB

Каноническое уравнение прямой:

Уравнение прямой BC

Каноническое уравнение прямой:

В) угол θ между прямыми АВ и ВС;

Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле: 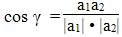где a1a2 = X1X2 + Y1Y2

Найдем угол между сторонами BA и BC

γ = arccos(0.45) = 63.440

Г) расстояние от точки С до прямой АВ. Уравнение перпендикуляра к прямой АВ, проходящего через точку С. Координаты точки пересечения прямой АВ и перпендикуляра;

Длина высоты треугольника, проведенной из вершины C

Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:

Найдем расстояние между точкой C(15;17) и прямой AB (4y + 3x — 13 = 0)

Уравнение высоты через вершину C

Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой

Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:

Найдем точку пересечения с прямой AB:

Имеем систему из двух уравнений:

Из первого уравнения выражаем y и подставим во второе уравнение.

Получаем: x = 3, y = 1

Д) уравнение прямой, проходящей через точку С параллельно прямой АВ;

Уравнение прямой, проходящей через данную точку С(x1, y1) в данном направлении, определяемом угловым коэффициентом k, y — y1 = k(x — x1).

Это уравнение определяет пучок прямых, проходящих через точку С(x1, y1), которая называется центром пучка. А k — это коэффициент при х уравнения прямой АВ

Тогда получим

Е) построим чертеж

Задания 11-20. Решить систему уравнений двумя способами (по формулам Крамера и методом Гаусса)

№12.

По формулам Крамера.

Запишем систему в виде:

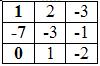
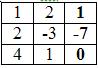
∆ = 1 • (-3 • (-2)-1 • (-1))-2 • (2 • (-2)-1 • (-3))+4 • (2 • (-1)-(-3 • (-3))) = -35 = -35

Заменим 1-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆1 = 1 • (-3 • (-2)-1 • (-1))-(-7 • (2 • (-2)-1 • (-3)))+0 • (2 • (-1)-(-3 • (-3))) = 0

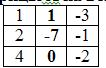
Заменим 2-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆2 = 1 • (-7 • (-2)-0 • (-1))-2 • (1 • (-2)-0 • (-3))+4 • (1 • (-1)-(-7 • (-3))) = -70

Заменим 3-ый столбец матрицы А на вектор результата В.

Найдем определитель полученной матрицы.

∆3 = 1 • (-3 • 0-1 • (-7))-2 • (2 • 0-1 • 1)+4 • (2 • (-7)-(-3 • 1)) = -35

Выпишем отдельно найденные переменные: , ,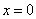

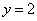
Запишем систему в виде расширенной матрицы:

Умножим 1-ую строку на (2). Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой:

Умножим 2-ую строку на (2). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:

Добавим 2-ую строку к 1-ой:

Теперь исходную систему можно записать как:

Из 1-ой строки выражаем z:

Из 2-ой строки выражаем у:

Из 3-ой строки выражаем x:

Введение в математический анализ.

Производная и ее приложения.

Задания 21-30. Найти указанные пределы, не пользуясь правилом Лопиталя:

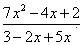
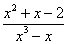
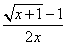
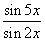
№22. а) ;б) ;в);г);д)

А) ;

Б) ;

В) ;

Г) ;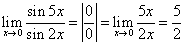

Использовали 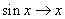при

Д)

Задания 31-40. Задана функция y=ƒ(x). Найти все точки разрыва функции, если они существуют. Построить график функции.

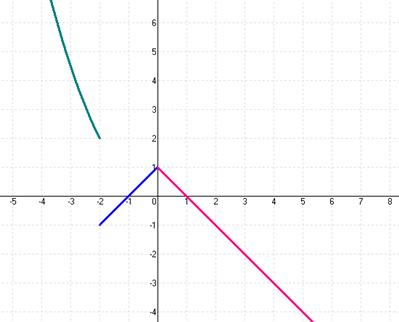
№32.

Построим график данной функции:

Функция определена на всём множестве чисел и неэлементарная.

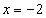
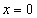
Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .

Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,

, . Так как , Следовательно функция имеет разрыв 1-го рода – скачок.

, . Так как , то в этой точке функция в этой точке непрерывна

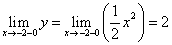
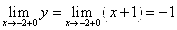
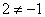
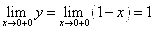
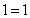
Задания 41-50. Найти производные первого порядка y’= 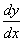функций:

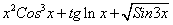
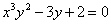
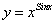
№42. а); б) ; в) ;

Д) ,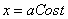

А) ;

Б) ;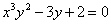

Дифференцируем обе части равенства по х:

Разрешаем равенство относительно :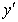

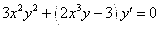
, тогда

Окончательно:

В) ;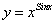

Прологарифмируем данную функцию:

Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.

Отсюда:

Д) ,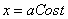

Находим и

Отсюда

Задания 51-60. Вычислить приближенно, заменяя приращение функции ее дифференциалом.

№52.

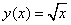
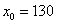
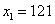
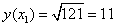
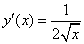
Рассмотрим функцию . Выберем, соответственно, , . Найдём значения функции и её производной:

, ,

Используя формулу для приближённых вычислений, 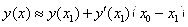, получим:

№Задания 61-70. Заданную функцию исследовать методами дифференциального исчисления. На основании результатов исследований построить график функции.

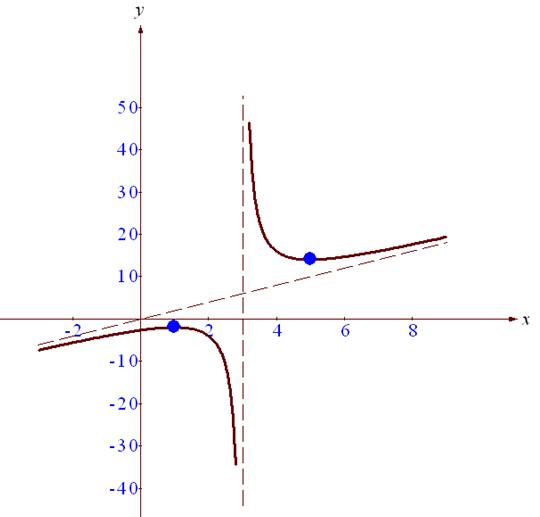
№62. ;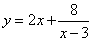

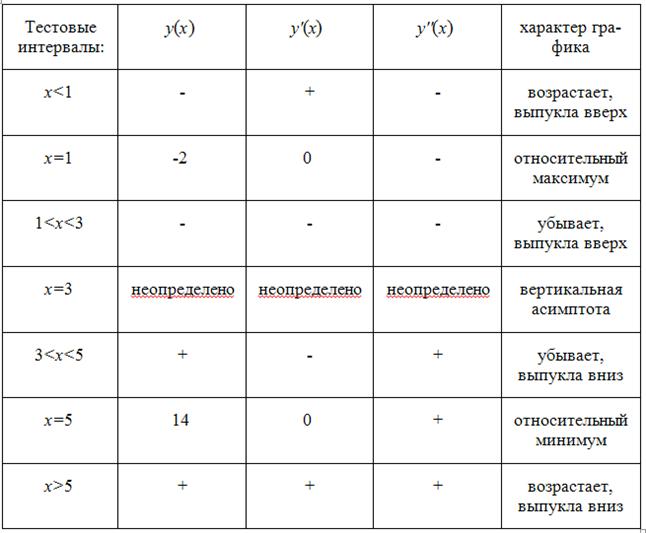
Исследуем функцию, заданную формулой:

Область определения:

Полученное решение отметим на рисунке.

Точки пересечения с осью : нет

, , — нет решений.

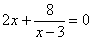
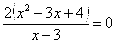
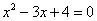
Точки пересечения с осью у:

Пусть х=0:

Вертикальные асимптоты: х=3

Горизонтальные асимптоты: нет.

Наклонные асимптоты: у=2х.

Предел разности исходной функции и функции 2х на бесконечности равен нулю.

Первая производная:

==

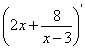
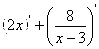
Критические точки: х=1, х=5

Случай.

Следующее уравнение равносильно предыдущему.

, , х-3=2, х=5

Случай .

Следующее уравнение равносильно предыдущему.

, , , х=1

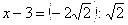
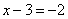
Вторая производная:

Возможные точки перегиба: нет

Точки разрыва: х=3

Симметрия относительно оси ординат: нет

Симметрия относительно начала координат: нет

Результаты исследования функции занесем в таблицу.

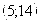
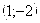
Относительный минимум . Относительный максимум .

Данные таблицы нанесем на координатную плоскость.

Используя результаты исследования функции, построим ее график.

Множество значений функции:

Наименьшее значение: нет

Наибольшее значение: нет

Задания 71-80. Найти интегралы.

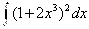
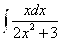
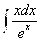
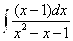
№72. а) ; б) ; в) ; г) ;

А) ;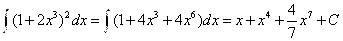

Б) ;

В) ;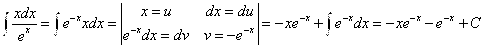

Г)

Задания 81-90. Вычислить несобственный интеграл или показать его расходимость

№82. ;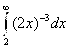

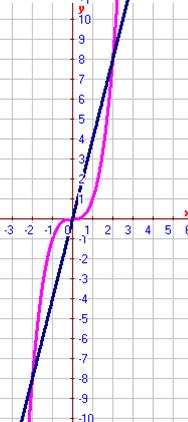
Задания 91-100. Найти площадь фигуры, ограниченной заданными линиями. Сделать рисунок.

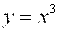
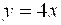
№92. и ;

Данные линии ограничивают две одинаковые по площади фигуры.

Тогда будем искать площадь одной части. Имеем

По формуле 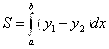. В нашем случае

Тогда

Ответ: 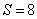кв. ед.

Функции нескольких переменных

Задания 101-110. Исследовать на экстремум функцию.

№102. ;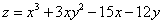

Необходимое условие существования єкстремума

, — критические точки, подозрительные на экстремум.

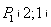
Используем достаточные условия экстремума

Найдем

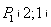
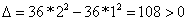
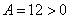
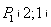
Для точки , — экстремум есть, а так как то в т. — минимум

Для точки , — экстремума нет.

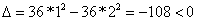
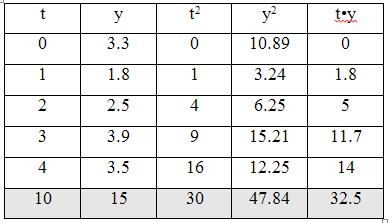
Задания 111-120. Экспериментально получены значения функции при пяти значениях аргумента, которые записаны в таблице. Предполагая, что между и имеется линейная зависимость, методом наименьших квадратов найти эмпирическую формулу (вычислить параметры и )

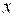
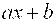
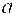
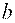
Линейное уравнение тренда имеет вид y = bt + a

1. Находим параметры уравнения методом наименьших квадратов.

Система уравнений метода наименьших квадратов:

Для наших данных система уравнений имеет вид:

10a0 + 30a1 = 32.5

Из первого уравнения выражаем а0 и подставим во второе уравнение

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Решение задач «Комплесные числа, исследование функции, векторная геометрия»,
Математика

Комплесные числа, исследование функции, векторная геометрия

ID (номер) заказа

Доброго времени суток, у меня остались три нерешенные задачи , а именно: 1)Исследовать на непрерывность функцию y = f(x), найти точки разрыва и определить их род. Построить схематический график функции. 2)Дано комплексное число z. Требуется: 1) записать число z в алгебраической, тригонометрической и показательной формах; 2) найти все корни уравнения w3+z=0, изобразить эти корни на плоскости комплексной переменной. 3)Даны координаты точек A1, A2, A3, A4. Известно, что отрезки A1A2, A1A3, A1A4 являются смежными ребрами параллелепипеда. Требуется найти: 1) длину ребра A1A2 ; 2) угол между ребрами A1A2 и A1A3 ; 3) площадь грани, содержащей вершины A1,A2,A3 ; 4) объем параллелепипеда; 5) уравнение прямой, проходящей через вершину A1 вдоль диагонали параллелепипеда; 6) уравнение плоскости A1A2A3; 7) угол между ребром A1A4 и гранью, содержащей вершины A1,A2,A3; 8) расстояние от вершины A4 до плоскости A1,A2,A3. Выполнить чертеж.

Закажите подобную или любую другую работу недорого

Вы работаете с экспертами напрямую,
не переплачивая посредникам, поэтому
наши цены в 2-3 раза ниже

Последние размещенные задания

Необходимо доработать, дипломную работу.

Срок сдачи к 27 апр.

Заполнение ведомости углов поворота

Срок сдачи к 29 апр.

Тема: Организация работы службы обслуживания в номерах.

Курсовая, Организация гостиничного дела

Срок сдачи к 1 мая

Проектирование сварного изделия, количество страниц.

Срок сдачи к 27 апр.

Домашняя контрольная работа

Контрольная, физическая культура

Срок сдачи к 30 апр.

Соглашение об уплате алиментов.

Реферат, семейное право

Срок сдачи к 26 апр.

Мне нужна дипломная работа на тему»Основы питания человека

Срок сдачи к 15 мая

Компактність метричних просторів. Лінійні нормовані простори. Еквівалентність норм.

📽️ Видео

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнения стороны треугольника и медианыСкачать

УРАВНЕНИЕ ПРЯМОЙСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

11. Прямая в пространстве и ее уравненияСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Видеоурок "Общие уравнения прямой"Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Уравнение прямой, проходящей через данную точку в данном направленииСкачать