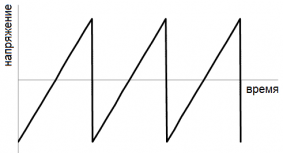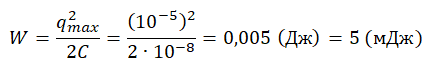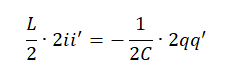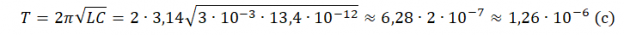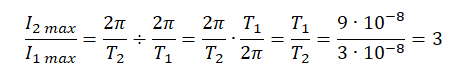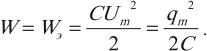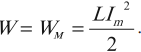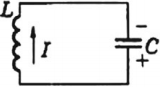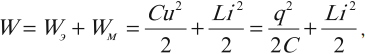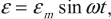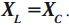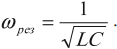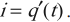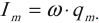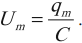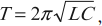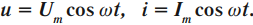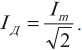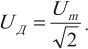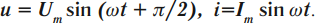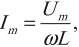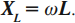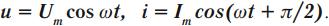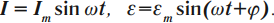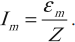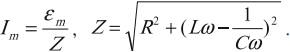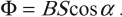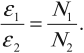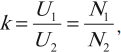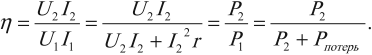Электромагнитные колебания и волны
Для колебательного контура предыдущей задачи написать уравнение (с числовыми коэффициентами) изменения со временем t энергии электрического поля Wэл, энергии магнитного поля Wм и полной энергии поля W. Найти энергию электрического поля, энергию магнитного поля и полную энергию поля в моменты времени Т/8, Т/4 и Т/2. Построить графики этих зависимостей в пределах одного периода.
Дано:
q = 2,5 мкКл = 2,5·10 -6 Кл
Решение:
Энергия электрического поля на обкладках конденсатора
Энергия магнитного поля в катушке индуктивности
Полная энергия в контуре
Закон изменения напряжения на обкладках конденсатора
Период колебаний находим по формуле Томсона
Циклическая частота связана с периодом соотношением
Уравнение колебания напряжения запишется в виде
Аналогично можно записать уравнение изменения заряда на обкладках конденсатора
Ток в контуре – первая производная от заряда по времени
- Электромагнитные колебания
- теория по физике 🧲 колебания и волны
- Осциллограф
- Колебательный контур
- Сходство электромагнитных колебаний в контуре со свободными механическими колебаниями
- Соответствие между механическими и электрическими величинами при колебательных процессах
- Уравнение, описывающее процессы в колебательном контуре
- Формула Томсона
- Гармонические колебания заряда и тока
- Автоколебания
- Электромагнитные колебания и волны
- Свободные электромагнитные колебания. Колебательный контур
- Вынужденные электромагнитные колебания. Резонанс
- Гармонические электромагнитные колебания
- Переменный ток. Производство, передача и потребление электрической энергии
- Емкостное сопротивление
- Электромагнитное поле
- Свойства электромагнитных волн
- Различные виды электромагнитных излучений и их применение
- 📽️ Видео
Видео:Физика 11 класс (Урок№7 - Свободные и вынужденные электромагнитные колебания. Колебательный контур.)Скачать

Электромагнитные колебания
теория по физике 🧲 колебания и волны
Заставить колебаться можно любую материю. Так, колебаться могут не только физические тела, состоящие из вещества, но и электромагнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами. Когда происходят колебания в механической системе, говорят, что тело совершает периодически повторяющиеся движения — оно отклоняется от положения равновесия то в одну, то в другую сторону. Когда происходят электромагнитные колебания, говорят, что электромагнитное поле периодически изменяется во времени, то есть его характеристики, то уменьшаются, то увеличиваются относительного некоторого среднего значения, которое является для них «положением равновесия».
Электромагнитные колебания — периодическое изменение во времени напряженности и индукции электромагнитного поля.
Напомним, что напряженность E представляет собой количественную характеристику электромагнитного поля, а индукция B — силовую. Причем электромагнитное поле — это взаимосвязанные между собой электрическое и магнитные поля. Так, проводник с током создает вокруг себя магнитное поле. Оно тем сильнее, чем выше сила тока в этом проводнике, которая напрямую зависит от напряжения в нем (или количества заряда, прошедшего через него за единицу времени). Поэтому изменения напряжения и силы тока в проводнике вызывают изменения напряженности и индукции магнитного поля. Следовательно, можно сделать вывод, что:
Электромагнитные колебания — периодические или почти периодические изменения во времени заряда, силы тока или напряжения.
Видео:Превращение энергии при электромагнитных колебаниях | Физика 11 класс #11 | ИнфоурокСкачать

Осциллограф
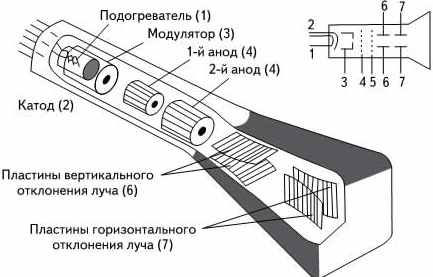
Но если колебания физических тел наблюдать легко, то колебания электромагнитного поля обнаружить без специальных приборов нельзя. Ведь увидеть изменения заряда, силы тока или напряжения невозможно. Использовать для этого электроизмерительные приборы (гальванометры, вольтметры или амперметры) тоже неудобно, поскольку электромагнитные колебания происходят с гораздо большей частотой по сравнению с механическими. Поэтому специально для визуализации электромагнитных колебаний был создан прибор, который называется осциллографом.
Осциллограф, схему которого вы видите ниже, представляет собой электронно-лучевую трубку. Через нее проходит узкий пучок электронов и попадает на экран, который начинает светиться при бомбардировке электронами.
На горизонтально отклоненные пластины трубки подается переменное напряжение развертки up пилообразной формы (см. рисунок ниже). Оно медленно нарастает и быстро падает. Поэтому электрическое поле между пластинами заставляет электронный луч пробегать экран в горизонтальном направлении с постоянной скоростью и затем почти мгновенно возвращаться назад. После этого весь процесс повторяется.
Если же присоединить вертикально отклоняющие пластины трубки к конденсатору, то колебания напряжения при его разрядке вызовут колебания луча в вертикальном направлении. В результате на экране осциллографа образуется временная развертка колебаний. Она напоминает синусоиду или косинусоиду подобно той, с помощью которой можно описать механические колебания.
С течением времени электромагнитные колебания затухают. Такие колебания являются свободными. Напомним, что свободными колебаниями называют такие колебания, которые возникают в колебательной системе после выведения ее из положения равновесия. В нашем случае система выводится из равновесия при сообщении конденсатору заряда. Зарядка конденсатора эквивалента отклонения математического маятника от положения равновесия.
В электрической цепи также можно получить вынужденные колебания, которые будут происходить до тех пор, пока на колебательную систему действует периодическая внешняя сила. Вынужденными электромагнитными колебаниями называют колебания в цепи под действием внешней периодической электродвижущей силы.
Видео:Урок 353. Колебательный контурСкачать

Колебательный контур
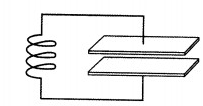
Колебательный контур — простейшая система, к которой могут происходить свободные электромагнитные колебания.
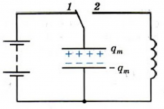
Колебательный контур состоит из конденсатора и катушки, присоединенной к его обкладкам (см. рисунок выше). Попробуем выяснить, почему в этом контуре возникают электромагнитные колебания. Для этого зарядим конденсатор, присоединив его на некоторое время к батарее с помощью переключателя (см. схему ниже).
При этом конденсатор получит энергию, равную:
W p = q 2 m a x 2 C . .
где q m a x — заряд конденсатора, а C — его электроемкость. Между обкладками конденсатора возникает разность потенциалов U m a x .
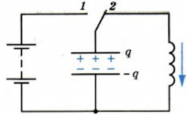
Теперь переведем переключатель в положение 2 (см. схему ниже). После этого конденсатор начнет разряжаться, и в цепи появится электрический ток. Сила тока достигнет максимального значения не сразу, а будет увеличиваться постепенно. Это объясняется явлением самоиндукции. При появлении тока возникает переменное магнитное поле. Это переменное магнитное поле порождает вихревое электрическое поле в проводнике. Вихревое электрическое поле при возрастании магнитного поля действует против тока и препятствует его мгновенному увеличению.
По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля тока, которая определяется формулой:
где i — сила переменного тока, L — индуктивность катушки.
Полная энергия W электромагнитного контура равна сумме энергий магнитного и электрического полей:
W = L i 2 2 . . + q 2 2 C . .
В момент, когда конденсатор полностью разрядится (q = 0), энергия электрического поля станет равной нулю. Но согласно закону сохранения энергии, максимальное значение обретет энергия магнитного поля. Сила тока в этот момент примет максимальное значение Imax.
К этому моменту разность потенциалов на концах катушки становится равной нулю. Но, несмотря на это, электрический ток не может исчезнуть сразу. Этому снова препятствует явление самоиндукции. Как только сила тока и созданное им магнитное поле начнут уменьшаться, возникает вихревое электрическое поле, которое поддерживает ток.
Конденсатор будет перезаряжаться до тех пор, пока сила тока, постепенно уменьшаясь, не станет равной нулю. Энергия магнитного поля в этот момент тоже будет равна нулю, а энергия электрического поля конденсатора опять будет максимальной. После этого конденсатор снова начнет перезаряжаться, и система вернется в исходное состояние.
Из-за частичных потерь энергии электромагнитные колебания являются затухающими. Если бы потерь не было, полная энергия система была бы постоянной и была бы равной:
W = L i 2 2 . . + q 2 2 C . . = q 2 m a x 2 C . . = L I 2 m a x 2 . .
Пример №1. После того как конденсатору колебательного контура был сообщен заряд q = 10 –5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нем полностью затухнут? Емкость конденсатора C = 0,01 мкФ.
0,01 мкФ = 10 –8 Ф
Поскольку с каждым колебанием колебательный контур теряет часть энергии в виде выделения тепла, ко времени, когда колебания полностью затухнут, выделится полная электромагнитная энергия системы. Ее можно определить формулой:
Сходство электромагнитных колебаний в контуре со свободными механическими колебаниями
Электромагнитные колебания в контуре имеют сходство со свободными механическими колебаниями (к примеру, колебаниями тела, закрепленного на пружине). Сходство относится не к природе самих величин, которые периодически изменяются, а к процессам периодического изменения различных величин.
Соответствие между механическими и электрическими величинами при колебательных процессах
| Механическая величина | Электрическая величина |
| Координата x | Заряд q |
| Скорость v x | Сила тока i |
| Масса m | Индуктивность L |
| Жесткость пружины | Величина, обратная емкости 1 C . . |
| Потенциальная энергия растянутой пружины k x 2 2 . . | Энергия электрического поля q 2 2 C . . |
| Кинетическая энергия m v 2 x 2 . . | Энергия магнитного поля L i 2 2 . . |
Уравнение, описывающее процессы в колебательном контуре
Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (см. схему ниже).
Полная электромагнитная энергия равна сумме энергий магнитного и электрического полей:
W = L i 2 2 . . + q 2 2 C . .
Если его сопротивление равно 0, то полная механическая энергия с течением времени не меняется. А производная константы равна нулю. Следовательно, сумма производных от каждой составляющей этой энергии также равна нулю.
( L i 2 2 . . ) ′ + ( q 2 2 C . . ) ′ = 0
( L i 2 2 . . ) ′ = − ( q 2 2 C . . ) ′
Первая производная по времени характеризует скорость изменения физической величины. Следовательно, эта формула позволяет сделать вывод о том, что скорость изменения энергии магнитного поля равна скорости изменения электрического поля. Знак «минус» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля уменьшается (и наоборот).
Вычислив обе производные, получим:
Но производная заряда по времени представляет собой силу тока в данный момент времени:
i = lim Δ t → 0 . Δ q Δ t . . = q ′
Поэтому мы можем записать уравнение иначе:
Производная силы тока по времени представляет собой вторую производную заряда по времени:
Подставив это равенство в уравнение, и преобразовав его путем деления на величину Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:
Формула Томсона
Когда мы рассматривали механические колебания, то вводили величину, постоянную для конкретной колебательной системы — коэффициент k m . . . Он представляет собой квадрат собственной частоты колебаний. По аналогии в случае с электромагнитными колебаниями этот коэффициент равен 1 L C . . . Он также представляет собой квадрат циклической частоты свободных электрических колебаний:
Следовательно, период свободных колебаний в контуре равен:
T = 2 π ω 0 . . = 2 π √ L C
Эта формула называется формулой Томсона.
Пример №2. Колебательный контур состоит из катушки индуктивностью L = 0,003 Гн и плоского конденсатора емкостью C = 13,4 пФ. Определите период свободных колебаний в контуре.
13,4 пФ = 13,4∙10 –12 Ф
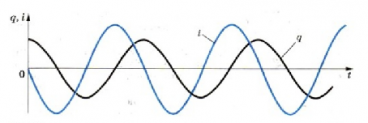
Гармонические колебания заряда и тока
Заряд конденсатора меняется с течением времени подобно тому, как координата при механических колебаниях изменяется со временем по гармоническому закону (в случае, когда в начальный момент времени отклонение от положения равновесия максимально):
q = q m a x cos . ω 0 t
где q m a x — амплитуда колебаний заряда.
Сила тока также совершает гармонические колебания:
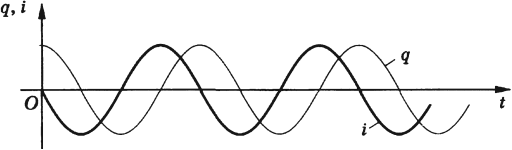
i = q ‘ = − ω 0 q m a x sin . ω 0 t = I m a x cos . ( ω 0 t + π 2 . . )
где I m a x — амплитуда колебаний силы тока, равная произведению циклической частоты на амплитуду колебаний заряда:
I m a x = q m a x ω 0
Колебания силы тока опережают по фазе на π 2 . . колебания заряда, что хорошо видно на рисунке ниже.
Пример №3. В двух идеальных колебательных контурах с одинаковой индуктивностью происходят свободные электромагнитные колебания, причём период колебаний в первом контуре 9⋅10 −8 с, во втором 3⋅10 −8 с. Во сколько раз амплитудное значение силы тока во втором контуре больше, чем в первом, если максимальный заряд конденсаторов в обоих случаях одинаков?
Максимальная сила тока равна:
I m a x = q m a x ω 0
Так как максимальный заряд конденсаторов одинаков в обоих контурах, отношение силы тока во тором контуре к силе ток в первом контуре равно:
I 2 m a x I 1 m a x . . = q m a x ω 02 q m a x ω 01 . . = ω 02 ω 01 . .
Циклическую частоту выразим из формулы Томсона:
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Автоколебания
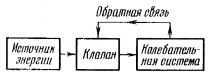
Незатухающие вынужденные колебания поддерживаются в цепи действием внешнего периодического напряжения. Но существует способ создания незатухающих колебаний, при котором колебательная система сама регулирует поступление энергии в колебательный контур для компенсации потерь энергии на резисторе.
Автоколебательные системы — системы, в которых генерируются незатухающие колебания за счет поступления энергии от источника тока внутри системы.
Автоколебания — незатухающие колебания, существующие в системе без воздействия на нее внешних периодических сил.
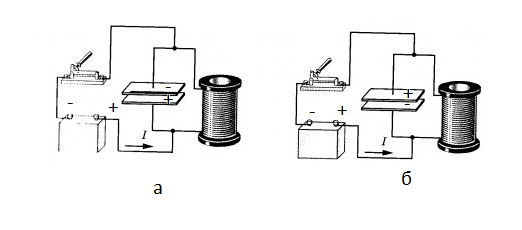
Самый простой пример автоколебательной системы — это генератор на транзисторе. Транзистор представляет собой полупроводниковое устройство, состоящее из эмиттера, базы и коллектора и имеющее 2 p–n перехода. Колебания тока в контуре вызывают колебания напряжения между эмиттером и базой, которые, в свою очередь, управляют силой тока в цепи колебательного контура (обратная связь). От источника напряжения в контур поступает энергия, компенсирующая потери энергии в контуре на транзисторе.
Схема автоколебательной системы представлена ниже.
Преимуществом такой схемы является то, что конденсатор при этом подключается к источнику тока только тогда, когда присоединенная к положительному источнику тока пластина конденсатора заряжена положительно (рис. а). Только в этом случае конденсатор восполняет потери энергии, выделенной на резисторе.
Если бы источник тока был включен всегда, восполнения потерь не происходило бы. Поскольку конденсатор разряжался бы в момент, когда он соединен с источником тока пластиной, заряженной отрицательно (рис. б).
В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора в первом контуре.
Видео:Свободные электромагнитные колебания. 11 класс.Скачать

Электромагнитные колебания и волны
Видео:Колебательный контур | ЕГЭ Физика | Николай НьютонСкачать

Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
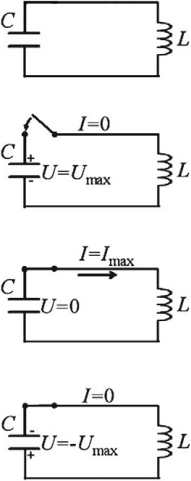
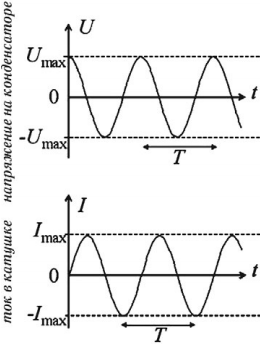
Если зарядить конденсатор до напряжения ( U_m ) , то в начальный момент времени ( t_1=0 ) , напряжение на конденсаторе будет равно ( U_m ) . Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ) . Сила тока равна нулю.
Полная энергия системы будет равна энергии электрического поля:
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ) . Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ) , напряжение равно ( U_m ) , сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ) , система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Видео:Урок 354. Математическое описание процессов в колебательном контуреСкачать

Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
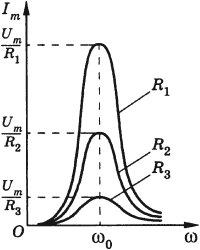
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ) , а на конденсаторе ( varphi_C=pi/2 ) . Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
Резонансная частота вычисляется по формуле:
Важно!
Резонансная частота не зависит от активного сопротивления ( R ) . Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ) , то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ) , напряжения – ( U_m ) и заряда – ( q_m ) .
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
Амплитуда колебаний силы тока равна:
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ) .
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Видео:Классические уравнения | колебательный контур | вывод уравнения при помощи закона сохранения энергииСкачать

Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ) . (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline
=frac. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке:
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Видео:КАК НА САМОМ ДЕЛЕ РАБОТАЕТ КОЛЕБАТЕЛЬНЫЙ КОНТУР?Скачать

Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ) . Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ) .
Если ввести обозначение ( X_C=frac ) , то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ) :
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
Если период вращения витка ( T ) , то угол ( alpha=frac=omega t ) .
Тогда ( Phi=BScosomega t. )
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10 -16 ;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 10 4 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ) :
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ) , взятой с противоположным знаком. Поэтому можно записать:
где ( k ) – коэффициент трансформации.
Если ( k>1 ) , то трансформатор понижающий, если ( k , то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ) : ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ) .
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ) , потребляемой нагрузкой, к мощности ( P_1 ) , потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
КПД трансформатора – 98%.
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Видео:Принцип работы колебательного контураСкачать

Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Видео:Уравнение колебательного контура.ФизикаСкачать

Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec ) и ( vec ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·10 8 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ) , единица измерения в СИ – ватт на квадратный метр (Вт/м 2 ).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Видео:Красота колебательных контуров!Скачать

Различные виды электромагнитных излучений и их применение
Электромагнитные излучения имеют длины волн от 10 -12 до 10 4 м или частоты от 3·10 4 до 3·10 20 .
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
Радиоволны
( lambda ) = 10 3 –10 -3 м, ( nu ) = 10 5 –10 11 Гц. Источники радиоволн – колебательный контур, вибратор.
Радиоволны делятся на:
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
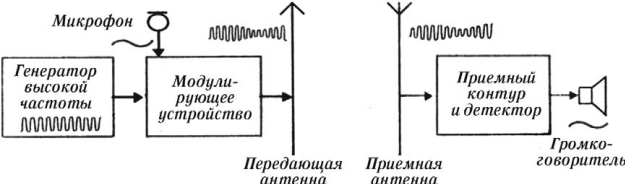
Схема радиосвязи показана на рисунке:
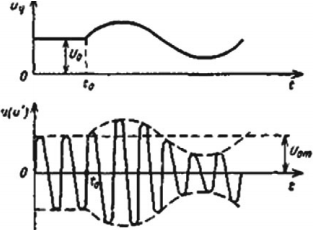
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
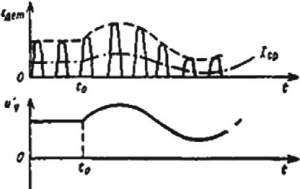
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10 -3 – 10 -7 м, ( nu ) = 10 11 – 10 14 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10 -7 – 4·10 -7 м, ( nu ) = 4·10 11 – 8·10 14 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10 -8 – 4·10 -7 м, ( nu ) = 8·10 14 – 3·10 15 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10 -8 – 10 -11 м, ( nu ) = 3·10 16 – 3·10 19 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10 -11 м, частота от 10 20 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·10 8 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac. )
Важно!
Амплитудное значение напряжения – ( U_m=frac ) , амплитудное значение силы тока – ( I_m=q_momega ) .
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
📽️ Видео
Закон сохранения энергии в колебательном контуреСкачать

Потенциальная и кинетическая энергияСкачать

Колебательный контур. Получение электромагнитных колебаний | Физика 9 класс #45 | ИнфоурокСкачать

Билеты №43,44 "Параметры колебательных контуров"Скачать

19 Колебательный контур.Скачать

ВСЕ задания на колебательный контур ЕГЭ. Часть 1Скачать

КОЛЕБАТЕЛЬНЫЙ КОНТУР | ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИСкачать