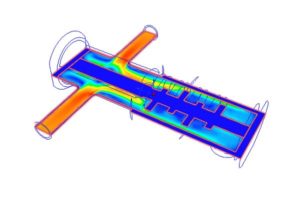
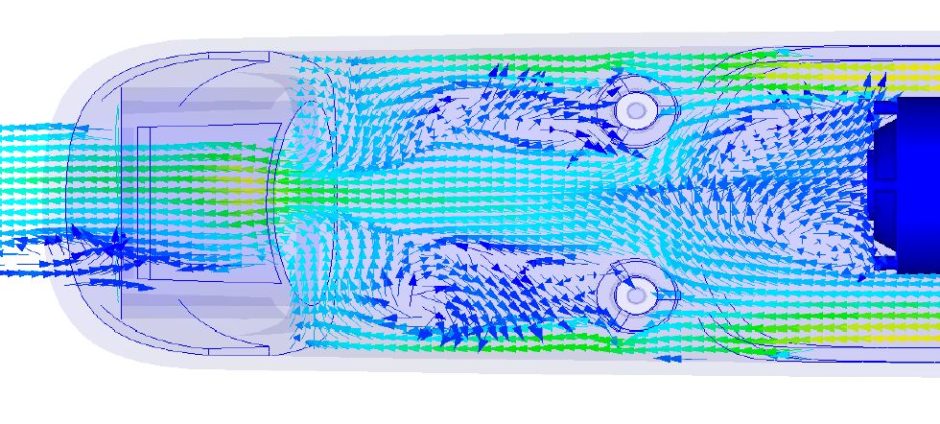
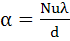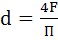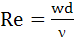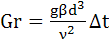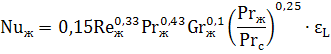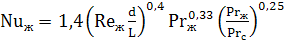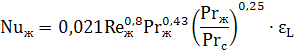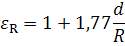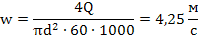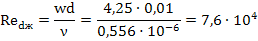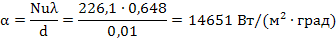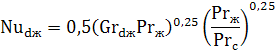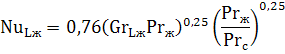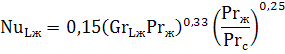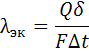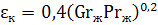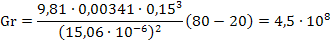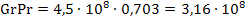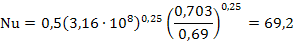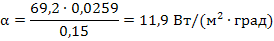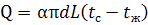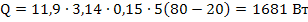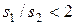Гидродинамика движения жидкости определяется числом Rежd=wd/v, где d – наружный диаметр трубы.
При небольших скоростях потока жидкости (Rежd 3 ) происходит отрыв ламинарного пограничного слоя от поверхности трубы, угол отрыва
φ=80-90 о . При значениях Rежd>10 5 ламинарное течение в пограничном слое сменяется турбулентным, угол отрыва турбулентного пограничного слоя от поверхности трубы составляет φ=120-140 о .

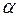
Коэффициент теплоотдачи принимает наибольшее значение на лобовой части трубы, где толщина пограничного слоя минимальная.
Из-за увеличения толщины пограничного слоя по периметру трубы коэффициент теплоотдачи уменьшается, достигая минимального значения в точке отрыва потока. В области циркуляционной зоны происходит увеличение коэффициента теплоотдачи за счет разрушения пограничного слоя. Для случая (в) первое увеличение коэффициента теплоотдачи связано со сменой режима течения в пограничном слое, второе – с отрывом турбулентного пограничного слоя.
Для расчета среднего по периметру трубы коэффициента теплоотдачи рекомендуются следующие уравнения:
 | (7.32) |
 | (7.33) |
 | (7.34) |
Формулы (7.31) – (7.34) действительны для случая, когда угол ψ между направлением потока жидкости и осью трубы, называемый углом атаки, равен 90 о . Если ψ о , то найденный по этим формулам коэффициент теплоотдачи следует умножить на поправочный коэффициент εψ=1- 0,54 cos 2 ψ.
В теплообменниках трубы располагаются в виде коридорных или шахматных пучков (рис.7.11).
 |
Геометрическими характеристиками пучка являются: поперечный (s1) и продольный (s2) шаги, наружный диаметр трубы (d), количество рядов труб (п) по направлению движения жидкости.
Режим течения жидкости в пучках может быть ламинарным, турбулентным или смешанным и определяется числом Rежd=wd/v, где d – наружный диаметр трубы.
При Rежd 3 – ламинарный режим;
при Rежd>10 5 – турбулентный;
при 10 3 5 – смешанный.
Экспериментальными исследованиями теплоотдачи в пучках установлено следующее:
1. При ламинарном режиме теплоотдача шахматных пучков выше, чем коридорных, при смешанном режиме эта разница уменьшается. При турбулентном режиме теплоотдача шахматных и коридорных пучков практически одинакова.
2. С увеличением номера ряда пучка теплоотдача возрастает благодаря увеличению турбулентности потока при прохождении его через пучок.
Начиная с третьего ряда и далее, структура потока остается практически неизменной и коэффициент теплоотдачи принимает постоянное значение.
Средние коэффициенты теплоотдачи для третьего и последующих рядов в пучках при поперечном омывании труб потоком жидкости рассчитываются по следующим уравнениям.
Для коридорных пучков:
— при 40 3 – ламинарный режим,
 | (7.35) |
— при 10 3 5 – смешанный режим,
 | (7.36) |
где εs=(s2/d) -0,15 – поправочный коэффициент, учитывающий плотность расположения труб в пучке;
— при Rежd>10 5 – турбулентный режим,
 | (7.37) |
Коэффициент теплоотдачи первого ряда коридорного пучка 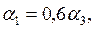


Для шахматных пучков:
 | (7.38) |
 | (7.39) |
если s1/s2 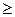
— при Rежd>10 5 коэффициент теплоотдачи шахматных пучков рассчитывается по уравнению (7.37).
Коэффициент теплоотдачи первого ряда шахматного пучка 
Уравнения (7.35) – (7.39) справедливы для угла атаки ψ=90 о . При ψ о уменьшение коэффициента теплоотдачи следует учесть коэффициентом
Конвективный теплообмен между трубами пучка и потоком жидкости рассчитывают по уравнению
 | (7.40) |
где F, м 2 – площадь поверхности всех труб пучка.
Средний коэффициент теплоотдачи пучка рассчитывается по формуле
 |
где п – число рядов.
 | (7.41) |
Контрольные вопросы и задания
1. Для парового котла высотой h=14 м с температурой поверхности обмуровки tc=40 о С и температурой воздуха в цехе tж=20 о С определите режим течения жидкости (воздуха) в пограничном слое при х= h.
Какие режимы течения жидкости имеют место по высоте поверхности обмуровки и какова протяженность участков с этими режимами?
2. Выведите формулы (7.12) и (7.13) с учетом (7.8) – (7.10) и уравнения теплового баланса Qэкв=Qк+т+Qл.
3. Можно ли уравнениями (7.20) и (7.21) воспользоваться для расчетов коэффициентов теплоотдачи:
а) при омывании труб продольным потоком жидкости;
б) при расчетах теплообмена между обшивкой летящего самолета и потоком воздуха, омывающего поверхность обшивки?
4. Какие режимы и при каких условиях имеют место в случае вынужденного течения жидкости в трубах? Сравните по коэффициенту теплоотдачи ламинарный и турбулентный режимы, вязкостный и вязкостно-гравитационный режимы. Дайте обоснование ответа.
5. Запишите формулу для определения коэффициента теплоотдачи при стабилизированном турбулентном течении жидкости в трубе. Подставьте в нее значения чисел Nu=ad/l, Re=wd/v, Pr=v/a=(v×cpr)/l и сделайте анализ зависимости
| a=f (d, w, l, v, cp, r). |
6. Сравните коэффициенты теплоотдачи при омывании трубы поперечным вынужденным потоком жидкости для угла атаки y=90 о и y=60 о . Во сколько раз они отличаются?
7. При каком режиме течения жидкости на теплоотдачу влияет плотность расположения труб в пучке?
Примеры решения задач
Задача № 1. Определить тепловые потери от паропровода диаметром d=200мм и длиной 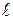
Учесть потерю теплоты излучением. Степень черноты поверхности паропровода принять ε=0,9.
Решение
Здесь имеет место теплоотдача при естественной конвекции в большом объеме. При температуре tж=30 о С для воздуха из табл.1 приложения имеем:


Температурный коэффициент объемного расширения воздуха вычисляем по формуле
 |
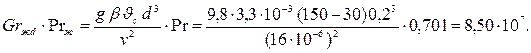 |
Так как (Grжd·Prж) 9 , то средний коэффициент теплоотдачи рассчитываем по уравнению (7.7):
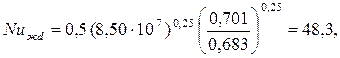 |
 |
Сомножитель для воздуха, 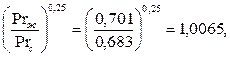
Потери тепла конвекцией
 |
 |
Суммарные тепловые потери паропровода составляют
| Q=Qк+Qл=24838 Вт. |
Задача № 2. Определить плотность теплового потока, проходящего через вертикальную щель толщиной δ=10 мм, заполненную воздухом. Температура горячей поверхности t1=180 о С, степень черноты ε1=0,9, холодной – t2=60 о С, ε2=0,5.
Решение
Между поверхностями, разделенными воздушной прослойкой, теплота передается теплопроводностью, конвекцией и излучением и может быть рассчитана по формуле
 |
При средней температуре воздуха 
Определяем температурный коэффициент объемного расширения
 |
и рассчитываем произведение чисел подобия
 |
Рассчитываем приведенную степень черноты поверхностей
и плотность лучистого потока

Задача № 3. По трубке внутренним диаметром 8 мм и длиной 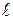

Определить коэффициент теплоотдачи и тепловой поток, передаваемый от стенки трубки к воде.
Решение
При средней температуре воды в трубке 
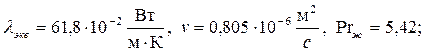 |
Определяем число Рейнольдса
 |
Режим течения турбулентный. По уравнению (7.28) рассчитываем средний коэффициент теплоотдачи от стенки трубки к воде. Так как 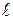
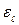
- Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах
- Теплоотдача при вынужденном течении жидкости в трубах и каналах
- Теплоотдача при ламинарном течении в трубах и каналах
- Теплоотдача в трубах и каналах при турбулентном режиме
- Расчет теплоотдачи при вынужденной конвекции
- Теплоотдача при свободной конвекции в трубах и каналах
- Свободная конвекция в неограниченном пространстве
- Свободная конвекция в ограниченном объеме
- Расчет теплоотдачи при свободной конвекции
- Теплообмен при поперечном обтекании пучка труб
- 📺 Видео
Видео:Основы конвективного теплообменаСкачать

Критериальные уравнения теплообмена: расчет теплоотдачи в трубах и каналах
Видео:Подобие процессов конвективного теплообменаСкачать

Теплоотдача при вынужденном течении жидкости в трубах и каналах
Теплоотдача в трубах и каналах может происходить при вынужденном или свободном характере конвекционных потоков (возможны также их сочетания в случае существенного влияния гравитационных сил).
При вынужденном течении (вынужденная конвекция) жидкость нагнетается или отводится под действием сил внешнего давления, например, ветра, насоса или вентилятора.
Свободное течение жидкости происходит под действием подъемных (гравитационных) сил за счет изменения ее плотности из-за разницы температуры – слой жидкости с меньшей плотностью стремиться занять верхнее положение относительно холодного слоя (свободная или естественная конвекция).
Интенсивность теплоотдачи, как при вынужденной, так и при свободной конвекции характеризуется коэффициентом теплоотдачи α, имеющим размерность Вт/(м 2 ·град), который определяется по формуле:
Nu – число Нуссельта; λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, равный
F – площадь сечения канала, м 2 ; П – периметр канала, м.
Для трубы круглого сечения, эквивалентный диаметр равен внутреннему диаметру трубы.
В целом, расчет коэффициента теплоотдачи сводится к определению числа Нуссельта, значение которого задается соответствующими критериальными уравнениями конвективного теплообмена, зависящими от режима течения жидкости и формы канала.
Течение жидкости в трубах определяется значением числа Рейнольдса Re и в зависимости от его величины может быть ламинарным, переходным или турбулентным.
- Ламинарный режим течения жидкости характеризуется величиной числа Re до 2300.
- При значении числа Re от 2300 до 10000 режим течения в трубах является переходным.
- Турбулентный режим течения в трубах наблюдается при числах Re более 10000.
Число (критерий) Рейнольдса представляет собой безразмерный комплекс, связывающий скоростные и вязкостные характеристики жидкости с определяющим размером канала (для трубы – это ее диаметр).
Число Re определяется по формуле:
w – скорость течения жидкости, м/с; d – эквивалентный диаметр канала, м; ν — кинематическая вязкость жидкости при средней температуре, м 2 /с.
Теплоотдача в трубах и каналах существенно зависит от режима течения жидкости. При ламинарном режиме интенсивность теплоотдачи значительно меньше, чем при развитом турбулентном.
Теплоотдача при ламинарном течении в трубах и каналах
Ламинарный режим течения жидкости обычно характеризуется низкой скоростью потока. При этом в некоторых случаях влиянием конвекции, обусловленной действием гравитационных сил, пренебрегать нельзя.
Для выбора правильного критериального уравнения теплообмена и оценки влияния естественной конвекции на интенсивность теплопередачи при ламинарном режиме служит критерий Грасгофа Gr.
g – ускорение свободного падения, м/с 2 ;
β – температурный коэффициент объемного расширения, град -1 ;
d – эквивалентный диаметр канала, м;
ν — кинематическая вязкость жидкости при средней температуре, м 2 /с;
Δt – средняя разность температур жидкости и стенки, °С.
Теплоотдача при ламинарном течении в трубах и каналах с учетом естественной конвекции. Если величина комплекса GrPr превышает 8·10 5 , то расчет коэффициента теплоотдачи необходимо проводить с учетом влияния естественной конвекции в потоке жидкости по следующему критериальному уравнению:
Индекс «ж» означает, что свойства среды, входящие в критерии подобия Re, Pr и Gr берутся при средней температуре жидкости.
Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки.
εL – коэффициент, учитывающий изменение теплоотдачи по длине трубы или канала. Его можно определить с помощью таблицы:
| L/d | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| εL | 1,9 | 1,7 | 1,44 | 1,28 | 1,18 | 1,13 | 1,05 | 1,02 | 1 |
Теплоотдача при ламинарном течении в трубах и каналах без учета естественной конвекции. При значении GrPr 5 , влияние естественной конвекции на теплоотдачу жидкости пренебрежительно мало, и расчет коэффициента теплоотдачи можно проводить по следующему критериальному уравнению:
d – эквивалентный диаметр канала, м;
L – длина трубы (канала), м.
Представленные критериальные уравнения теплообмена при ламинарном режиме позволяют определить среднее значение числа Нуссельта, по величине которого можно рассчитать средний коэффициент теплоотдачи:
λ – коэффициент теплопроводности жидкости при средней температуре, Вт/(м·град);
d – эквивалентный диаметр, м.
Теплоотдача в трубах и каналах при турбулентном режиме
Теплоотдача в трубах и каналах при турбулентном режиме осуществляется путем передачи тепла при интенсивном перемешивании слоев жидкости. Критериальное уравнение теплообмена для расчета средней теплоотдачи в трубах и каналах в этом случае имеет вид:
Критерии подобия Re и Pr берутся при средней температуре жидкости. Число Прандтля с индексом «с» Prс берется при температуре стенки.
Представленное критериальное уравнение применяется в диапазоне чисел Re от 1·10 4 до 5·10 6 и Pr от 0,6 до 2500.
εL – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы или канала при турбулентном режиме течения. Значения εL приведены в следующей таблице при различных числах Рейнольдса и отношениях длины канала к его эквивалентному диаметру:
| Reж | L/d | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 5 | 10 | 15 | 20 | 30 | 40 | 50 | |
| 1·10 4 | 1,65 | 1,5 | 1,34 | 1,23 | 1,17 | 1,13 | 1,07 | 1,03 | 1 |
| 2·10 4 | 1,51 | 1,4 | 1,27 | 1,18 | 1,13 | 1,1 | 1,05 | 1,02 | 1 |
| 5·10 4 | 1,34 | 1,27 | 1,18 | 1,13 | 1,1 | 1,08 | 1,04 | 1,02 | 1 |
| 1·10 5 | 1,28 | 1,22 | 1,15 | 1,1 | 1,08 | 1,06 | 1,03 | 1,02 | 1 |
| 1·10 6 | 1,14 | 1,11 | 1,08 | 1,05 | 1,04 | 1,03 | 1,02 | 1,01 | 1 |
Расчет теплоотдачи в изогнутых трубах и каналах проводится по тому же критериальному уравнению с добавлением множителя — поправки на действие центробежных сил, которая определяется по формуле:
R — радиус изгиба трубы или канала, м; d – эквивалентный диаметр трубы или канала, м.
Теплоотдача в изогнутых трубах проходит более интенсивно, чем в прямых, за счет большего вихреобразования и лучшего перемешивания жидкости.
Расчет теплоотдачи при вынужденной конвекции
Пример расчета. Рассчитаем средний коэффициент теплоотдачи воды, текущей по трубопроводу длиной 1 м, диаметром d=0,01 м с расходом Q=20 л/мин. Средняя температура воды tж=50°С, температура стенки трубы tс=10°С.
1. Определим физические свойства воды при температуре 50°С:
- Теплопроводность воды λж= 0,648 Вт/(м·град);
- Плотность воды ρж=988 кг/м 3 ;
- Кинематическая вязкость воды νж=0,556·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=3,54;
- Число Прандтля при температуре стенки Prс=9,52.
2. Рассчитаем среднюю скорость течения воды w по трубе:
3. Определим число Рейнольдса Re:
4. Поскольку число Рейнольдса имеет значение больше 1·10 4 , то режим течения является турбулентным и расчет теплоотдачи необходимо проводить по следующему критериальному уравнению:
Определим коэффициент εL по соотношению L/d=1/0,01=100. Поскольку L/d>50, то коэффициент εL=1.
Выполним расчет числа Нуссельта по приведенному критериальному уравнению:
5. Рассчитаем средний коэффициент теплоотдачи от воды к стенке трубы по формуле:
Таким образом, средний коэффициент теплоотдачи от воды к стенке трубы составляет 14,65 кВт/(м 2 ·град).
Видео:Диагностика трубного пучка кожухотрубного теплообменника. Как правильно повести диагностику.Скачать

Теплоотдача при свободной конвекции в трубах и каналах
Теплообмен при свободном движении жидкости (или газа) происходит вследствие разности плотностей нагретых и холодных ее слоев. Интенсивность теплоотдачи жидкости в трубах и каналах при свободной конвекции существенно зависит от их положения в пространстве относительно силы тяжести.
Теплоотдача при свободной конвекции имеет различный характер в случаях свободного течения в неограниченном пространстве и теплообмена в ограниченном объеме (в узкой трубе или канале).
Свободная конвекция в неограниченном пространстве
Конвекция в неограниченном пространстве протекает, например при охлаждении трубопровода центрального отопления, расположенного на улице в безветренную погоду, вблизи от которого отсутствуют препятствия для движения воздушных потоков.
Горизонтальный канал или труба. Интенсивность теплоотдачи при свободной конвекции зависит от величины комплекса GrPr. При значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу от поверхности горизонтальных труб и каналов, имеет вид:
В качестве определяющего размера принимается наружный диаметр d канала или трубы.
Вертикальный канал (труба, пластина). Для вертикальных труб и каналов при значении GrPr от 10 3 до 10 9 критериальное уравнение, описывающее среднюю теплоотдачу, имеет вид:
При GrPr>10 9 :
Примечание: В приведенных критериальных уравнениях теплообмена свойства жидкости, входящие в числа Gr и Pr, определяются при температуре окружающей среды. Число Прандтля с индексом «с» Prс берется для жидкости при температуре стенки. В качестве определяющего размера принимается длина L (высота) вертикально стоящей трубы или канала.
Свободная конвекция в ограниченном объеме
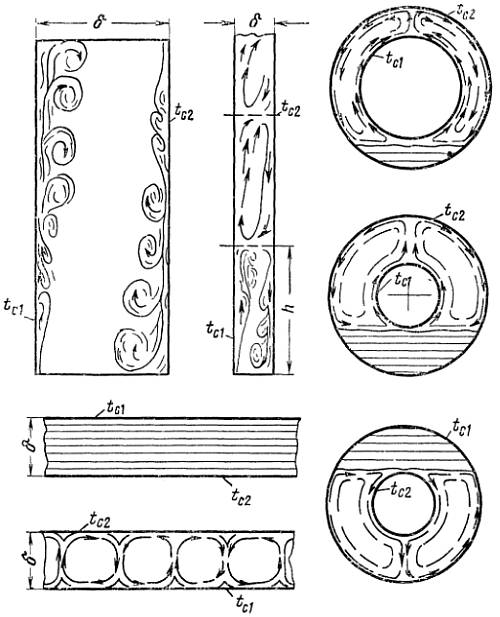
Теплообмен жидкости в ограниченном объеме при свободной конвекции характеризуется совместным протеканием процессов нагрева и охлаждения соседних слоев жидкости (или газа). Эти процессы сопровождаются сложным течением нисходящих и восходящих потоков, зависящих от рода жидкости, разницы температуры, формы канала и его геометрических размеров.
Для упрощения расчета таких сложных процессов конвективного теплообмена принято рассматривать их, как явление теплопроводности в щели толщиной δ с учетом понятия эквивалентного коэффициента теплопроводности λэк.
Эквивалентный коэффициент теплопроводности определяется по формуле:
Q — количество переданного тепла, Вт; δ — толщина слоя жидкости (или газа), м; F — площадь теплоотдающей поверхности, м 2 ; Δt=tc1-tc2 — температурный напор между нагретой и холодной стенками, °С.
Отношение эквивалентного коэффициента теплопроводности λэк к величине теплопроводности окружающей жидкости при средней температуре называется коэффициентом конвекции εк, который определяется значением комплекса GrPr.
При малых значениях комплекса GrPr 3 6 :
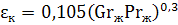
Примечание: Числа подобия Gr и Pr рассчитываются при средней температуре жидкости (или газа), равной tж=0,5(tc1+tc2). В качестве определяющего размера принимается δ — толщина слоя жидкости.
Расчет теплоотдачи при свободной конвекции
Пример расчета. Рассчитаем потери тепла естественной конвекцией от горизонтального трубопровода центрального отопления, находящегося на открытом воздухе. Диаметр трубопровода d=0,15 м, длина L=5 м, средняя температура наружной стенки tс=80°С. Температура окружающего воздуха tж=20°С.
1. Определим физические свойства воздуха при температуре 20°С:
- Теплопроводность воздуха λж= 0,0259 Вт/(м·град);
- Кинематическая вязкость воздуха νж=15,06·10 -6 , м 2 /с;
- Число Прандтля при температуре жидкости Prж=0,703;
- Число Прандтля при температуре стенки Prс=0,69;
- Коэффициент объемного расширения βж=1/(273+20)=0,00341 град -1 .
2. Вычислим число Грасгофа Gr по формуле:
3. Определим значение комплекса GrPr:
Этому значению комплекса соответствует следующее критериальное уравнение теплообмена при свободной конвекции в случае горизонтальной трубы:
4. Вычислим значение числа Нуссельта Nu:
5. Рассчитаем коэффициент теплоотдачи от трубы α по формуле:
6. Определим потери тепла с боковой поверхности трубопровода по формуле:
Подставляя численные значения, окончательно получаем потерю тепла:
Таким образом, только путем естественной (свободной) конвекции рассмотренный трубопровод отопления отдает воздуху 1681 Вт тепла.
Видео:Л1 - Теплопроводность. Закон Фурье.Скачать

Теплообмен при поперечном обтекании пучка труб
В технике большое практическое значение имеет конвективный теплообмен в пучках труб при расположении их перпендикулярно движению жидкости. Применяют в основном два вида расположения труб в пучках:
– коридорное (рис. 5.3);
– шахматное (рис. 5.4).
Характеристиками пучка труб считаются: диаметр трубы и относительные шаги по ширине 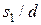




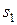
 |  | |
 |  |  |
При любом расположении труб каждый ряд вызывает дополнительную турбулизацию потока. Поэтому коэффициент теплоотдачи для труб второго ряда выше, чем для первого, а для третьего ряда – выше, чем для второго. Начиная с третьего ряда, поток жидкости стабилизируется, и коэффициент теплоотдачи для всех последующих рядов остается величиной постоянной. Если теплоотдачу третьего ряда принять за 100%, то теплоотдача первого ряда коридорных и шахматных пучков составляет лишь 60%. Теплоотдача второго ряда коридорного пучка составляет 90%, а шахматного – 70%. В целом теплоотдача в шахматных пучках вследствие лучшей турбулизации потока выше, чем в коридорных.
В поперечно обтекаемых пучках можно выделить три основных режима омывания: ламинарный, смешанный и турбулентный. Наиболее изученным является смешанный режим, которому соответствуют числа Re от 10 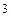
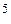
Для определения коэффициента теплоотдачи третьего и последующих рядов труб пучка при смешанном режиме ( 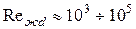
– при коридорном расположении труб
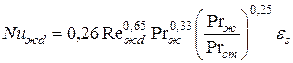
где 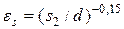
относительных шагов для глубинных рядов;
– при шахматном расположении труб
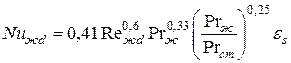
где при

при
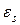
При вычислении критериев подобия за определяющую температуру принята средняя температура жидкости, за определяющую скорость – скорость в самом узком сечении ряда, за определяющий размер – диаметр трубы. Формулы справедливы для любых жидкостей.
Для двухатомных газов и воздуха эти формулы упрощаются и принимают следующий вид:
– при коридорном расположении труб

– при шахматном расположении труб
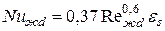
Значение коэффициента теплоотдачи для труб первого ряда определяется путем умножения коэффициента теплоотдачи для третьего ряда на поправочный коэффициент 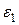


Среднее значение коэффициента теплоотдачи для всего пучка в целом определяется по формуле осреднения
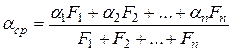
где 

📺 Видео
Возможности Ansys для расчета задач внешнего обтекания и теплообменаСкачать

Интуитивное понимание формулы теплопроводности (часть 11) | Термодинамика | ФизикаСкачать

ТеплопроводностьСкачать

Основные сведения о конструкциях теплообменниковСкачать

Учебный фильм - ТеплообменСкачать

Теплопроводность, конвекция, излучение. 8 класс.Скачать

Теплообмен при кипенииСкачать

Теплопередача. Виды теплопередачи | Физика 8 класс #2 | ИнфоурокСкачать

Физика 8 класс (Урок№2 - Теплопроводность, конвекция, излучение)Скачать

Теплообменник типа "труба в трубе". Конструкция и принцип работы.Скачать

Моделирование теплогидравлических процессов в пароводяных трактах котлоагрегатов в ПО FlownexСкачать

8.1 Решение уравнения теплопроводности на отрезкеСкачать

Тепловое расширение твёрдых телСкачать

Урок 106 (осн). Виды теплопередачи (часть 1)Скачать

Создание общей сборки кожухотрубчатого теплообменного аппарата (штуцера и опоры)Скачать

Теплопроводность, конвекция и тепловое излучение (часть 8) | Термодинамика | ФизикаСкачать