Уравнение плоской волны задачи с решениями (6 видео)

Примеры решенных задач по физике -Контрольная 1(гармонические колебания, плоские волны, кольца Ньютона, дифракция, поляризация света)

Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.

Точка совершает гармонические колебания с амплитудой А=10 см и периодом Т=5 с. О п ределите для точки : 1) максимальную скорость, 2) максимальное ускорение.

Дано : A =10 см=0 .1 м

Найти : v max , a max

Уравнение гармонического колебания точки имеет вид :

x = Acos ( ω t + φ ) (1)

Формулу скорости получим, взяв первую производную по времени от смещения :

v= 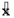=dx/dt=-A ω sin( ω t+ φ )

Максимальная скорость точки равна :

v max =- A ω (2) , где А – амплитуда колебаний ; ω – круговая частота колебаний.

Круговая частота колебаний ω связана с периодом колебаний Т выражением :

С учётом (3) формула (2) примет вид :

v max =-2 π A / T (4)

Ускорение точки найдём, взяв производную по времени от скорости :

a= 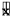=dv/dt=-A ω 2 cos( ω t+ φ )

Максимальное ускорение, равно :

С учётом (3) перепишем формулу (5) в виде :

a max =-4 π 2 A / T 2 (6)

Производя вычисления по формулам (4) и (6), найдём максимальные скорость и ускорение точки.

v max =-2×3.14×0.1/5=-0.13 м/с

a max =-4×3.14 2 ×0.1/5 2 =-0.16 м/с 2

Ответ : v max =-0.13 м/с ; a max =-0.16 м/с 2

Волна с периодом Т=1.2 с и амплитудой колебания А=2 см распространяется со скоростью 15 м/с. Чему равно смещение точки, находящейся на расстоянии 45 м от источника волн в тот момент, когда от начала колебаний источника прошло время t = 4 с ?

Уравнение плоской волны имеет вид :

y ( x , t )= Acos ( ω t — kx ) (1) , где y – смещение точек среды с к о ординатой x в момент времени t ; ω – круговая частота ; k – волновое число.

Волновое число k связано с длиной волны λ выражением :

k =2 π / λ (2) , где λ = vT ; v – скорость распространения колебаний ; T – период колебаний.

Циклическая частота ω связана с периодом Т выражением :

С учётом (2) и (3) уравнение (1) примет вид :

y(x,t)=Acos(2 π t/T-2 π x/(vT))=Acos 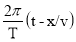(4 )

Вычисления по формуле (4), дают :

y (45 ; 4)=0.02× cos 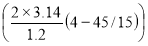=0.01 м=1 см

Ответ : y(45 ; 4)=1 см.

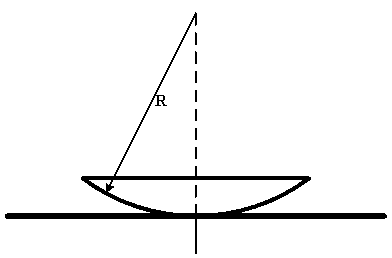
Определить радиус второго темного кольца Ньютона в отраженном свете, если прибор, состоящий из плосковыпуклой линзы с радиусом кривизны 8 м и плоской пластины освещается монохроматическим светом с длиной волны 640 нм.

Дано : λ =64 0 нм= 6.5×10 — 7 м

Радиус темных колец Ньютона в отражённом свете определяется формулой :

r k = 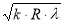(1)

где k – номер кольца ; R – радиус кривизны линзы ; λ – длина волны.

3,2∙10 — 3 м .

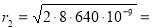
Ответ : r 2 = 3,2∙10 — 3 м .

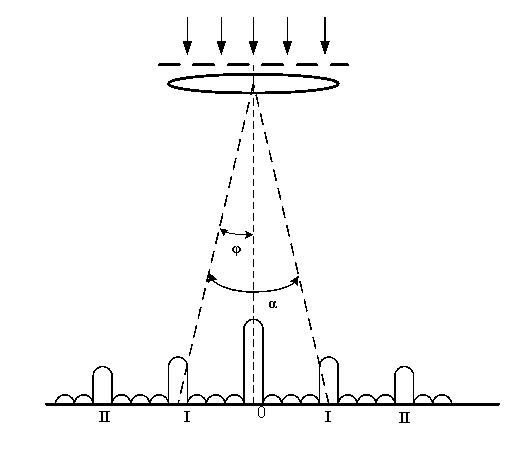
Постоянная дифракционной решётки в n =4 раза больше длины световой волны монохр о ма тического света, нормально падающего на её поверхность. Определить угол α между дв у мя первыми симметричными дифракционными максимумами.

Постоянная дифракционной решётки d , длина волны λ и угол  отклонения лучей соо т ветст вующий К – му дифракционному максимуму, связаны соотношением

dsin  = kλ , или sin  = kλ / d (1)

где к – порядок максимума (в данном случае к=1). Учитывая, что λ/ d =1/ n перепишем форм у лу (1) в виде:

Из рисунка видно, что угол α равен удвоенному углу  . Тогда формула (2) примет вид:

sin ( α /2)= k / n , откуда α=2 arcsin ( k / n )

Подставим в последнюю формулу числовые значения и вычислим:

На сколько процентов уменьшается интенсивность света после прохождения через призму Николя, если потери света составляют 10% ?

Естественный свет, падая на грань призмы Николя, расщепляется вследствие двойного л у чепреломления на два пучка : обыкновенный и необыкновенный. Оба пучка одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного пучка лежит в плоскости чертежа. Плоскость колебаний обыкновенного пучка перпенд и кулярна плоскости чертежа. Обыкновенный пучок (о) вследствие полного отражения от грани AB отбрасывается на зачернённую поверхность призмы и поглощается ею. Необы к новенный пучок (е) проходит через призму. При этом интенсивность света уменьшается вследствие поглощения в веществе николя. Таким образом, интенсивность света, пр о шедшего через призму :

где k = 0.1 – относительная потеря интенсивности света в николе ; I 0 – интенсивность е с тественного света, падающего на николь.

Относительное уменьшение интенсивности света получим, разделив интенсивность I 0 ест е ственного света, падающего на первый николь, на интенсивность I 1 поляризованного св е та :

(1)

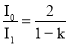
Вычисления по формуле (1) дают :

=2.2

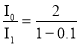
Процентное уменьшение интенсивности :

n % = 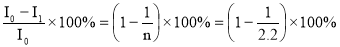=54.5 %

Ответ : при прохождения света через призму интенсивность уменьшится на 54.5%.

Найти длину волны де Бройля для электрона, движущегося по круговой орбите атома водорода, находящегося в основном состоянии.

Длина волны де Бройля λ частицы зависит от её импульса p и определяется формулой :

Импульс частицы можно определить, если известна её скорость v . Связь импульса со скоростью для нерелятивистского (когда v c ) и для релятивистского (когда v ≈ c ) случаев соответственно выражается формулами :

p=m 0 v (2) ; p= 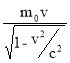(3)

Формула (1) с учётом соотношений (2) и (3) запишется соответственно в нерелятивис т ском и релятивистском случаях :

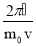
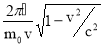
λ = (4) ; λ = (5)

Найдём скорость электрона на круговой орбите атома водорода, находящегося в осно в ном состоянии, из следующих соображений. Согласно теории Бора, радиус r электронной орбиты и скорость v электрона на ней связаны равенством mvr = n ħ . Так как нам требуется скорость электрона на первой орбите, то главное квантовое число n =1 и равенство примет вид :

Откуда скорость электрона :

v = 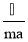(6)

где ħ – постоянная Планка (ħ= 1.05×10 -34 Дж·с) ; m – масса покоя электрона

( m =9.11×10 — 31 кг ) ; a – радиус первой орбиты (а= 5.29×10 — 11 м – Боровский радиус).

Найдём скорость электрона, произведя вычисления по формуле (6) :

v = 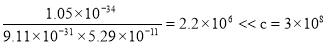м/с

Следовательно , можно применить формулу (4). С учётом (6) формула (4) примет вид :

Вычисления по формуле (7) дают :

λ =2×3.14×5.29×10 -11 =3.3×10 — 10 м

Ответ : λ =3.3×10 — 10 м .=0.33 нм.

Имя файла: physics1.doc

Размер файла: 456.5 Kb

Если закачивание файла не начнется через 10 сек, кликните по этой ссылке

Содержание

Примеры решения расчетных задач
Плоская волна
Определение и основные понятия плоской волны
Уравнение плоской волны
💡 Видео

Видео:Получение уравнения плоской бегущей волны.Скачать

Примеры решения расчетных задач

Ход занятия

Для выполнения задания необходимо вспомнить основные характеристики волны и записать в тетради: амплитуда волны, фаза волны. Также следует вывести уравнение стоячей волны, чтобы убедиться в том, что стоячая волна образуется в результате интерференции бегущей и отраженной волны.

Качественные задачи

1. В бегущей волне частица А имеет направление скорости, указанное на рис. 1. В каком направлении «движется» волна?

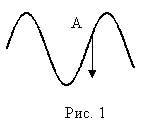
2. Почему не могут быть поперечными упругие волны в газе?

3. При образовании волн частицы воды не перемещаются вдоль направления их распространения, а лишь участвуют в колебательном движении около некоторого среднего положения. Почему же морское волнение часто выбрасывает на берег различные плавающие в море предметы?

4. Может ли существовать в природе плоская гармоническая волна, или это физическая идеализация, лишь приближенно описывающая реальность?

5. Могут ли космонавты при выходе в открытый космос общаться между собой при помощи звуковой речи?

6. В воду погружен вибратор, мембрана которого издает музыкальные звуки. Будет ли находящийся под водой пловец воспринимать мелодию такой же, какой он слышал бы ее в воздухе?

7. Перед игрой инструменты «настраивают». В чем физическая сущность настройки скрипки, мандолины и других струнных инструментов?

Примеры решения расчетных задач

Задача 1. Плоская волна с периодом Т = 1,2 с и амплитудой колебаний a = 2 см распространяется со скоростью v = 15 м/с. Чему равно смещение ξ(x,t) точки, находящейся на расстоянии х = 45 м от источника волн, в тот момент, когда от начала колебаний источника прошло время t = 4 с?

Воспользуемся уравнением плоской волны

. (1)
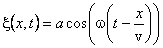
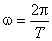
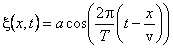
Частота связана с периодом колебаний соотношением . Подставим значение частоты в уравнение (1).

.
Подставляя в последнее выражение численные значения величин, получим

м.

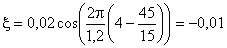
Задача 2. Две точки находятся на расстоянии Δx = 50 см друг от друга на прямой, вдоль которой распространяется плоская волна со скоростью v = 50 м/с. Период колебаний Т равен 0,05 с. Найдите разность фаз Δφ колебаний в этих точках.

Фаза плоской волны равна . Разность фаз в двух точках пространства, охваченного волновым процессом, в момент времени t определяется соотношением

.
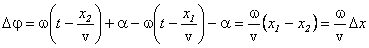
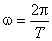
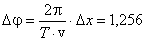
Подставляя численные значения и учитывая, что , получим

рад.

Задача 3. Звуковые колебания, имеющие частоту ν = 0,5 КГц и амплитуду a, равную 0,25 мм, распространяются в упругой среде. Длина волны λ = 70 см. Найдите:

1. скорость распространения волн;

2. максимальную скорость частиц среды.

Скорость распространения волны связана с длиной волны соотношением

λ = v·T, (2)
где Т — период колебаний частиц среды. Период колебаний связан с частотой колебаний ν соотношением

. (3)
Из (2) и (3) получим для скорости распространения волны

v = λ·ν = 350 м/с.
Для ответа на второй вопрос воспользуемся уравнением плоской волны

.
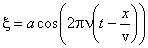
Чтобы найти скорость частиц среды, нужно взять производную от смещения по времени

.
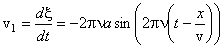
Отсюда видно, что максимальная скорость движения частиц среды будет равна

Задача 4. Две волны ξ₁ = asin(ωt-kx) и ξ₂ = asin(ωt+kx) с одинаковыми частотами ν = 4 Гц распространяются со скоростью v = 960 см/с. Они интерферируют между собой и образуют стоячую волну. Определите амплитуду точек стоячей волны через каждые l = 20 см, начиная отсчет от узла. Определите величину смещения и скорость этих точек в момент времени 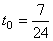с.

Стоячая волна возникает в результате интерференции при сложении ξ₁ и ξ₂.

ξ = ξ₁+ξ₂ = 2acos(kx)sin(2πνt).
Из уравнения стоячей волны видно, что в каждой точке пространства происходят колебания с частотой ω. При этом амплитуда колебаний в точке х равна

A = 2a|coskx|.
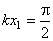
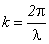
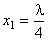
Следовательно, в точках, в которых coskx = 0 , колебания отсутствуют. Эти точки являются узлами стоячей волны. Координата первого узла определяется из соотношения . Учитывая, что , получим . Расстояние между двумя соседними узлами равно см.

Следовательно, между двумя узлами будет находиться n = 5 точек, удовлетворяющих условию задачи. Координаты этих точек будут равны

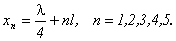
Амплитуда колебаний в этих точках определяется из условия:

.
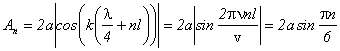
Подставляя значения n, получим A₁ = a , A₂ = 1,73a , A₃ = 2a , A₄ = 1,73a , A₅ = a .

Смещение найденных точек от положения равновесия можно найти из уравнения стоячей волны.

.
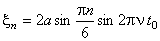
Подставляя численные значения, получим ξ₁ = 0,866a , ξ₂ = 1,5a , ξ₃ = 1,732a , ξ₄ = 1,5a , ξ₅ = 0,866a .
Чтобы найти скорость этих точек, нужно взять производную от смещения ξ по времени

.
Подставляя численные значения, получим: V₁ = 1,566a , V₂ = 2,174a , V₃ = 3,132a , V₄ = 2,174a , V₅ = 1,566a .

Задача 5. В упругой однородной среде распространяются две плоские волны — одна вдоль оси Х, другая вдоль оси Y: ξ₁ = acos(ωt-kx), ξ₂ = acos(ωt-ky). Найдите характер движения частиц среды в плоскости XY, если обе волны поперечные и направление колебаний одинаково.

Воспользуемся принципом суперпозиции волн, тогда результирующий волновой процесс будет описываться уравнением:

.
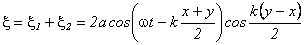
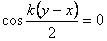
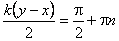
Из полученного уравнения видно, что в точках, для которых выполняется условие , колебания отсутствуют. Координаты этих точек будут удовлетворять условию , где n = 0, 1, 2, …
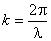
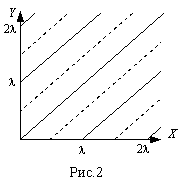
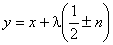
Учитывая, что волновое число , получим, что частицы среды не совершают колебания вдоль прямых, уравнения которых имеет вид

.
На рис. 2 эти прямые проведены пунктиром.

Если , частицы среды колеблются с максимальным отклонением. Этому условию удовлетворяют точки, координаты которых можно получить из условия , где n = 0, 1, 2, … После подстановки значения получим уравнение прямых y = x ± nλ. На рис. 2 эти прямые проведены сплошными линиями.

Видео:решение задач по теме механические колебания и волны 9 классСкачать

Плоская волна

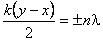
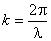
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Определение и основные понятия плоской волны

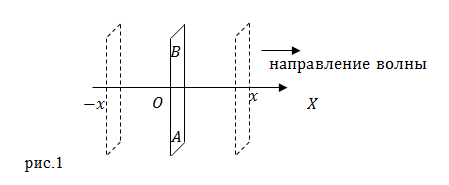
Пусть источником волн в бесконечной упругой среде является бесконечно большая пластина. Она совершает колебания вдоль оси X, плоскость пластины перпендикулярна оси X (рис.1).

Пластина совершает гармонические колебания. Введем следующие обозначения: $s_0$ — смещение точек пластины AB и примыкающих к ней частиц среды от положения равновесия; $A_0$ — амплитуда колебаний пластины; $varphi $ — фаза колебаний; $omega $ — циклическая частота колебаний. Уравнение колебаний пластины имеет вид:

В таком случае в среде распространяется гармоническая волна такой же частоты. Если среда является однородной и изотропной, то колебания всех частиц вещества на одинаковых расстояниях от пластины идентичны (совпадают амплитуды и начальные фазы колебаний). То есть волновые поверхности имеют вид параллельных плоскостей, которые перпендикулярны оси X (направлению волны). Данные волны называют плоскими.

Волны, волновые поверхности которых представляют собой плоскости, называют плоскими.

Видео:Волны. Основные понятия. Решение задач.Задача 1Скачать

Уравнение плоской волны

Колебания в точках среды, находящихся на расстоянии $x$ от плоскости AB отстают по фазе от колебаний источника на величину $kx$:

при отсутствии рассеяния энергии волны в веществе $A$=$A_0$. $k=frac $- волновое число.

Для точек пространства находящихся правее плоскости AB $x>0$, для точек находящихся левее этой плоскости $x Пример 1

Задание: Плоская гармоническая волна распространяется по прямой, которая совпадает с осью X, в положительном направлении оси. Среда энергию не поглощает. Скорость распространения волны равна $v$. Амплитуда волны $A.$ Две точки, которые находятся на расстояниях $x_1 и x_2$ от источника волны совершают колебания с разностью фаз $Delta varphi =frac$. Какова длина волны? Запишите уравнение волны.

Решение: Запишем уравнение плоской волны:

Фазы колебаний двух точек в этой волне равны:

[_1=omega t-kx_1+varphi ;; _2=omega t-kx_2+varphi left(1.3right).]

Найдем их разность:

[Delta varphi =omega t-kx_2+varphi -left(omega t-kx_1+varphi right)=kleft(x_2-x_1right)=fracleft(x_2-x_1right)left(1.4right).]

Выразим длину волны ($lambda $) из (1.4):

Для написания уравнения волны через известные из условий задачи величины используем формулу:

Можем записать уравнение волны:

Задание: В однородном упругом веществе имеется плоская стоячая волна вида: $s=A$. Нарисуйте графики зависимости $sleft(xright)$ при $t=0$ и $t=frac$, где $T$ — период колебаний.