Уравнение плоской электромагнитной волны распространяющейся вдоль оси oy (6 видео)

2.6. Электромагнитные волны

Любой колебательный контур излучает энергию. Изменяющееся электрическое поле возбуждает в окружающем пространстве переменное магнитное поле, и наоборот. Математические уравнения, описывающие связь магнитного и электрического полей, были выведены Максвеллом и носят его имя. Запишем уравнения Максвелла в дифференциальной форме для случая, когда отсутствуют электрические заряды () и токи (j = 0):

Величины и — электрическая и магнитная постоянные, соответственно, которые связаны со скоростью света в вакууме соотношением

Постоянные и характеризуют электрические и магнитные свойства среды, которую мы будем считать однородной и изотропной.

В отсутствие зарядов и токов невозможно существование статических электрического и магнитного полей. Однако переменное электрическое поле возбуждает магнитное поле, и наоборот, переменное магнитное поле создает электрическое поле. Поэтому имеются решения уравнений Максвелла в вакууме, в отсутствие зарядов и токов, где электрические и магнитные поля оказываются неразрывно связанными друг с другом. В теории Максвелла впервые были объединены два фундаментальных взаимодействия, ранее считавшихся независимыми. Поэтому мы говорим теперь об электромагнитном поле.

Колебательный процесс в контуре сопровождается изменением окружающего его поля. Изменения, происходящие в окружающем пространстве, распространяются от точки к точке с определенной скоростью, то есть колебательный контур излучает в окружающее его пространство энергию электромагнитного поля.

Электромагнитная волна — это распространяющееся в пространстве электромагнитное поле, в котором напряженность электрического и индукция магнитного полей изменяются по периодическому закону.

При строго гармоническом изменении во времени векторов и электромагнитная волна называется монохроматической.

Получим из уравнений Максвелла волновые уравнения для векторов и .

Волновое уравнение для электромагнитных волн

Как уже отмечалось в предыдущей части курса, ротор (rot) и дивергенция (div) — это некоторые операции дифференцирования, производимые по определенным правилам над векторами. Ниже мы познакомимся с ними поближе.

Возьмем ротор от обеих частей уравнения

При этом воспользуемся доказываемой в курсе математики формулой:

где — введенный выше лапласиан. Первое слагаемое в правой части равно нулю в силу другого уравнения Максвелла:

Получаем в итоге:

Выразим rotB через электрическое поле с помощью уравнения Максвелла:

и используем это выражение в правой части (2.93). В результате приходим к уравнению:

и вводя показатель преломления среды

запишем уравнение для вектора напряженности электрического поля в виде:

Сравнивая с (2.69), убеждаемся, что мы получили волновое уравнение, где v — фазовая скорость света в среде:

Взяв ротор от обеих частей уравнения Максвелла

и действуя аналогичным образом, придем к волновому уравнению для магнитного поля:

Полученные волновые уравнения для и означают, что электромагнитное поле может существовать в виде электромагнитных волн, фазовая скорость которых равна

В отсутствие среды (при ) скорость электромагнитных волн совпадает со скоростью света в вакууме.

Основные свойства электромагнитных волн

Рассмотрим плоскую монохроматическую электромагнитную волну, распространяющуюся вдоль оси х:

Возможность существования таких решений следует из полученных волновых уравнений. Однако напряженности электрического и магнитного полей не являются независимыми друг от друга. Связь между ними можно установить, подставляя решения (2.99) в уравнения Максвелла. Дифференциальную операцию rot, применяемую к некоторому векторному полю А можно символически записать как детерминант:

Подставляя сюда выражения (2.99), зависящие только от координаты x, находим:

Дифференцирование плоских волн по времени дает:

Тогда из уравнений Максвелла следует:

Отсюда следует, во-первых, что электрическое и магнитное поля колеблются в фазе:

Далее, ни у , ни у нет компонент параллельных оси х:

Иными словами и в изотропной среде,

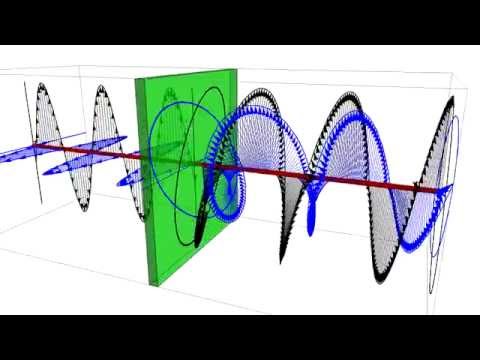
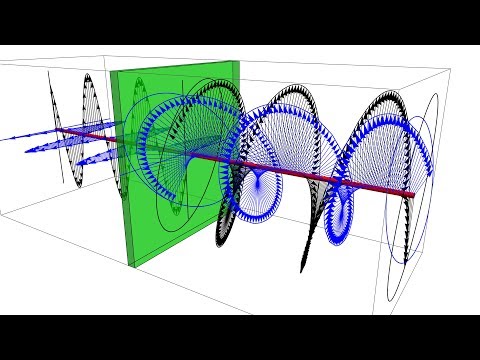
электромагнитные волны поперечны: колебания векторов электрического и магнитного полей происходят в плоскости, ортогональной направлению распространения волны.

Тогда можно выбрать координатные оси так, чтобы вектор был направлен вдоль оси у (рис. 2.27):

Рис. 2.27. Колебания электрического и магнитного полей в плоской электромагнитной волне

В этом случае уравнения (2.103) приобретают вид:

Отсюда следует, что вектор направлен вдоль оси z:

Иначе говоря, векторы электрического и магнитного поля ортогональны друг другу и оба — направлению распространения волны. С учетом этого факта уравнения (2.104) еще более упрощаются:

Отсюда вытекает обычная связь волнового вектора, частоты и скорости:

а также связь амплитуд колебаний полей:

Отметим, что связь (2.107) имеет место не только для максимальных значений (амплитуд) модулей векторов напряженности электрического и магнитного поля волны, но и для текущих — в любой момент времени.

Итак, из уравнений Максвелла следует, что электромагнитные волны распространяются в вакууме со скоростью света. В свое время этот вывод произвел огромное впечатление. Стало ясно, что не только электричество и магнетизм являются разными проявлениями одного и того же взаимодействия. Все световые явления, оптика, также стали предметом теории электромагнетизма. Различия в восприятии человеком электромагнитных волн связаны с их частотой или длиной волны.

Шкала электромагнитных волн представляет собой непрерывную последовательность частот (и длин волн) электромагнитного излучения. Теория электромагнитных волн Максвелла позволяет установить, что в природе существуют электромагнитные волны различных длин, образованные различными вибраторами (источниками). В зависимости от способов получения электромагнитных волн их разделяют на несколько диапазонов частот (или длин волн).

На рис. 2.28 представлена шкала электромагнитных волн.

Рис. 2.28. Шкала электромагнитных волн

Видно, что диапазоны волн различных типов перекрывают друг друга. Следовательно, волны таких длин можно получить различными способами. Принципиальных различий между ними нет, поскольку все они являются электромагнитными волнами, порожденными колеблющимися заряженными частицами.

Уравнения Максвелла приводят также к выводу о поперечности электромагнитных волн в вакууме (и в изотропной среде): векторы напряженности электрического и магнитного полей ортогональны друг другу и направлению распространения волны.

http://www.femto.com.ua/articles/part_1/0560.html – Волновое уравнение. Материал из Физической Энциклопедии.

http://elementy.ru/trefil/24 – Уравнения Максвелла. Материал из «Элементов».

http://telecomclub.org/?q=node/1750 – Уравнения Максвелла и их физический смысл.

http://principact.ru/content/view/188/115/ – Кратко об уравнениях максвелла для электромагнитного поля.

Эффект Доплера для электромагнитных волн

Пусть в некоторой инерциальной системе отсчета К распространяется плоская электромагнитная волна. Фаза волны имеет вид:

Наблюдатель в другой инерциальной системе отсчета К’, движущейся относительно первой со скоростью V вдоль оси x, также наблюдает эту волну, но пользуется другими координатами и временем: t’, r’. Связь между системами отсчета дается преобразованиями Лоренца:

Подставим эти выражения в выражение для фазы , чтобы получить фазу волны в движущейся системе отсчета:

Это выражение можно записать как

где и — циклическая частота и волновой вектор относительно движущейся системы отсчета. Сравнивая с (2.110), находим преобразования Лоренца для частоты и волнового вектора:

Для электромагнитной волны в вакууме

Пусть направление распространения волны составляет в первой системе отсчета угол с осью х:

Тогда выражение для частоты волны в движущейся системе отсчета принимает вид:

Это и есть формула Доплера для электромагнитных волн.

Если , то наблюдатель удаляется от источника излучения и воспринимаемая им частота волны уменьшается:

Если , то наблюдатель приближается к источнику и частота излучения для него увеличивается:

При скоростях V 2 (солнечная постоянная). Найдем среднюю амплитуду колебаний E₀ вектора электрической напряженности в солнечном излучении. Вычислим амплитуды колебаний напряженности магнитного поля H₀ и вектора магнитной индукции B₀ в волне.

Ответ находим сразу из уравнений (3.127), где полагаем :

Электромагнитные волны поглощаются и отражаются телами, следовательно, они должны оказывать на тела давление. Рассмотрим плоскую электромагнитную волну, падающую нормально на плоскую проводящую поверхность. В этом случае электрическое поле волны возбуждает в теле ток, пропорциональный Е. Магнитное поле волны по закону Ампера будет действовать на ток с силой, направление которой совпадает с направлением распространения волны. В 1899 г. в исключительно тонких экспериментах П.И. Лебедев доказал существование светового давления. Можно показать, что волна, несущая энергию W, обладает и импульсом:

Пусть электромагнитная волна падает в вакууме по нормали на площадь А и полностью поглощается ею. Предположим, что за время площадка получила от волны энергию . Тогда переданный площадке импульс равен

На площадку действует со стороны волны сила

Давление Р, оказываемое волной, равно

Если средняя плотность энергии в волне равна , то на площадь А за время попадет энергия из объема и

Отсюда находим давление электромагнитной волны (света):

Если площадка идеально отражает всю падающую на нее энергию, то давление будет в два раза большим, что объясняется очень просто: одинаковый вклад в давление в этом случае дают как падающая, так и отраженная волны, в случае полностью поглощающей поверхности отраженной волны просто нет.

Пример 3. Найдем давление Р солнечного света на Землю. Используем значение солнечной постоянной из предыдущего примера. Искомое давление равно:

Пример 4. Найдем давление Р лазерного пучка на поглощающую мишень. Выходная мощность лазера N = 4.6 Вт, диаметр пучка d = 2.6 мм.

Содержание

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
20.1. Волновое уравнение для электромагнитной волны.
Расчетно-графические задания по физике
Министерство образования Российской Федерации
Ивановский государственный энергетический университет
Кафедра физики
Составители: М. В. Дмитриев,
Рецензент
🌟 Видео

Видео:Поляризация плоской электромагнитной волныСкачать

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

Видео:Получение уравнения плоской бегущей волны.Скачать

20.1. Волновое уравнение для электромагнитной волны.

Основные свойства электромагнитной волны: скорость, поперенность, связь между ? и я

Из уравнений Максвелла следует, что электромагнитное поле способно существовать самостоятельно — без электрических зарядов и токов. Взаимосвязанные колебания (изменения) электрического и магнитного полей, составляющих единое электромагнитное поле, называются электромагнитными колебаниями.

Электромагнитные волны — это электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью. В вакууме они всегда распространяются со скоростью, равной скорости света с.

Именно присутствие тока смещения db/dt наряду с величиной dB/dt и означает возможность появления электромагнитных волн. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение же поля электрического в свою очередь возбуждает магнитное поле. За счет непрерывного взаимопревращения электромагнитное возмущение будет распространяться в пространстве.

Рассмотрим однородную изотропную нейтральную непроводящую среду

где ?₀ и ц₀ — соответственно электрическая и магнитная постоянные; ? и р — соответственно диэлектрическая и магнитная проницаемости среды. Используя уравнения Максвелла, можно показать, что волновые уравнения для векторов Е п Н имеют вид

где V = Д = —у+—т + тт — оператор Лапласа. дх ду dz

Перечислим основные свойства электромагнитных волн, распространяющихся в изотропной нейтральной непроводящей неферромагнитной среде.

1. Скоростью распространения и электромагнитной волны в среде называется фазовая скорость (скорость распространения фазы колебаний). По закону Максвелла

где с = /^?₀|i₀ — скорость распространения электромагнитной волны в вакууме. Поскольку ?р > 1, то v лу — круговая (циклическая) частота этих колебаний;

к — (.o/v — волновое число; а — начальная фаза колебаний волны при / = О их = 0. Знак «минус» в скобках уравнений (20.5) и (20.5а) означает, что волна распространяется в положительном направлении оси X. Отметим, что амплитуды электрического и магнитного полей Е_т и Н_т связаны соотношением (20.4).

Расстояние, на которое распространяется электромагнитная волна в среде за время одного периода колебаний Т, называется длиной волны и определяется как

Связь длины электромагнитной волны с периодом Т и частотой v колебаний в вакууме выражается так:

Волновые уравнения плоской гармонической электромагнитной волны,

распространяющейся вдоль оси X, записываются как

Видео:Урок 384. Излучение электромагнитных волн.Скачать

Расчетно-графические задания по физике

Видео:Билеты № 35, 39 "Плоская волна, ее отражение. Давление излучения"Скачать

Министерство образования Российской Федерации

Видео:Билет №34 "Электромагнитные волны"Скачать

Ивановский государственный энергетический университет

Видео:Раскрытие тайн электромагнитной волныСкачать

Кафедра физики

ВОЛНОВЫЕ И КВАНТОВЫЕ СВОЙСТВА СВЕТА

Расчетно-графические задания по физике

Иваново 2004

Видео:4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать

Составители: М. В. Дмитриев,

Настоящие задания предназначены для обеспечения самостоятельной работы студентов по теме “Волны. Волновые и квантовые свойства света”.

В заданиях учтены особенности учебных планов различных факультетов. Дана таблица вариантов контрольной работы для студентов заочной формы обучения.

Расчетно–графические задания утверждены цикловой методической комиссией ИФФ

Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Рецензент

кафедра физики Ивановского государственного энергетического университета

1. Упругие и электромагнитные волны.
Общая характеристика волновых процессов

Уравнение плоской волны, распространяющейся вдоль оси X, имеет вид:

где – смещение частицы среды, имеющей координату в момент времени ; – амплитуда смещения; – циклическая частота; – волновое число; – начальная фаза.

Для одномерной волны уравнение волновой поверхности имеет вид:

Скорость перемещения волновой поверхности равна:

где – длина волны; – период колебаний; – частота колебаний.

Уравнение волны, распространяющейся в среде с затуханием:

где – коэффициент затухания; – амплитуда волны в точке .

Объёмная плотность энергии упругой волны:

где – плотность среды.

Плотность потока энергии упругой волны (вектор Умова), распространяющейся в среде со скоростью , равна:

Поток энергии, переносимый волной через поверхность площадью , равен:

где – угол между вектором скорости и единичным вектором нормали к поверхности .

Уравнение плоской электромагнитной волны:

где , – амплитуды векторов напряженности электрического и магнитного поля соответственно. Модули амплитуды векторов напряжённости магнитного и электрического поля связаны соотношением:

где – относительная диэлектрическая проницаемость среды,
– относительная магнитная проницаемость среды, – электрическая постоянная, – магнитная постоянная. Фазовая скорость волны:

здесь – скорость электромагнитной волны в вакууме; – показатель преломления среды.

Объемная плотность энергии электромагнитной волны:

Плотность потока энергии электромагнитной волны, называемая вектором Пойнтинга, равна:

где – групповая скорость волны. В среде, обладающей дисперсией, групповая скорость связана с фазовой скоростью волны соотношением:

В вакууме вектор Пойнтинга равен :

Интенсивность электромагнитной волны:

Давление плоской электромагнитной волны:

где – коэффициент отражения, – угол между направлением распространения волны и нормалью к поверхности.

Коэффициент отражения света в случае его падения по нормали к поверхности равен:

где – интенсивность отраженного света, – интенсивность падающего света, – относительный показатель преломления вещества.

Задача 1. Тонкая длинная струна с закрепленными концами натянута вдоль координатной оси Х. Если вывести струну из положения равновесия, то все частицы струны движутся перпендикулярно ее положению равновесия (поперечные колебания). В каждый момент времени струна находится в плоскости ХОУ. В процессе колебания величина отклонения частиц струны от положения равновесия y зависит от координаты x и времени t. Найти зависимость y(x, t).

Решение. При фиксированном значении t график функции y(x,t) представляет форму колеблющейся струны в момент времени t (рис.1).

Частная производная dy/dx= дает угловой коэффициент к касательной в точке с абсциссой х.

Для заданного значения х функция y(x,t) определяет закон движения точки струны с координатой х вдоль прямой, параллельной оси OY, производная есть скорость движения этой точки, вторая производная – ускорение.

Выделим бесконечно малый участок струны М1М2, проектирующейся на ось ОХ интервалом [x,x+dx]. На него действуют силы натяжения и . При малых колебаниях частиц струны угол наклона касательной к любой точке струны мал, . Приняв, что величина силы натяжения вдоль струны постоянна и равна , получим

где

Здесь частное приращение производной при переходе от аргументов (х, t) к аргументам (x+dx,t) заменено ее частным дифференциалом

Масса участка струны равна

где – линейная плотность вещества струны (кг/м).

Запишем второй закон Ньютона для этого участка:

Обе части уравнения разделим на и получим уравнение:

где – положительная постоянная величина.

Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами называется одномерным волновым уравнением. Оно описывает свободные колебания струны.

В случае бесконечно длинной струны общее решение волнового уравнения имеет вид:

Функция в момент времени t=0 описывает перемещение волны вдоль оси ОХ в положительном направлении со скоростью V, которая равна . Функция описывает волну, распространяющуюся вдоль оси ОХ в обратном направлении.

Если точки струны колеблются по гармоническому закону то вдоль струны будет распространяться волна со скоростью V, описываемая гармонической функцией.

Задача 2. Смещение от положения равновесия точки, находящейся на расстоянии 4см от источника колебаний, в момент времени t=T/6 равно половине амплитуды. Найти длину волны.

Решение. В уравнении плоской волны подставим и выразим из него в явном виде длину волны:

Подставим числовые данные:

Задача 3. По какому закону изменяется с расстоянием амплитуда незатухающей цилиндрической воны?

Решение. Поток энергии, переносимой волной через цилиндрическую поверхность радиуса R, пропорционален интенсивности волны и площади поверхности S

где h – высота цилиндра. Этот же поток энергии переносится волной и через цилиндрическую поверхность радиуса r. Следовательно,

Интенсивность волны пропорциональна квадрату амплитуды

Если источником волн является тонкая нить; то амплитуда выбирается равной амплитуде волны на расстоянии R=1 м от оси нити. Закон убывания амплитуды с расстоянием от источника принимает вид:

1.1. Написать уравнение плоской монохроматической волны, распространяющейся вдоль оси Х. Частицы среды колеблются вдоль оси Z. Известно, что амплитуда волны равна А, циклическая частота ω, начальная фаза π/6, длина λ. Рассеянием энергии пренебречь.

1.2. Получить дифференциальное уравнение, решением которого является функция

1.3. Получить дифференциальное уравнение, решением которого является функция Какой физический смысл имеет коэффициент ?

1.4. Плоская монохроматическая волна распространяется вдоль оси Υ. Амплитуда волны А=0,05 м. Считая, что в начальный момент времени смещение точки Р, находящейся в источнике, максимально, определить смещение от положения равновесия точки М, находящейся на расстоянии y=λ/2 от источника колебаний в момент времени t=T/6.

1.5. В условии задачи 1.4 определить разность фаз колебаний точек М и Р.

1.6. В некоторый момент времени t1 в точке х1=0 фаза плоской монохроматической волны равна нулю. Какова будет фаза волны в точке х2=10-3 м в тот же момент времени? Какова будет фаза волны в точке х2 в момент времени t2=10-2 c? Длина волны λ=10-4 м.

1.7. Плоские волны переходят из среды, в которой фазовая скорость волны равна V, в среду, в которой фазовая скорость в два раза больше. Что происходит при этом с частотой и длиной волны ?

1.8. Какие из приведённых функций можно использовать при описании волновых движений: , , ?

1.9. Записать уравнение цилиндрической волны. Установить закон, по которому меняется амплитуда и интенсивность цилиндрической волны с изменением расстояния от источника.

1.10. Записать уравнение сферической волны. Установить закон, по которому меняется амплитуда и интенсивность сферической волны с изменением расстояния от источника.

1.11. В окрестностях точек 1 и 2 известны направления распространения сферической волны (рис.1.1). Найти графическим построением положение источника излучения.

1.12. В поглощающей среде вдоль оси Х распространяется плоская волна. Определить расстояние, на котором амплитуда волны уменьшается в е раз. Коэффициент затухания волны известен и равен .

1.13. Указать направление, вдоль которого распространяется плоская волна, имеющая волновой вектор (k,0,0). Определить частоту ν и длину λ этой волны. Скорость распространения волны в среде равна V.

1.14. Решить задачу 1.13, приняв волновой вектор равным (0,k,0).

1.15. Решить задачу 1.13, приняв волновой вектор равным (0,0,-k).

1.16. На больших расстояниях от точечного источника сферическая волна может рассматриваться как плоская. При каком характерном размере d малый участок волновой поверхности может считаться плоским? Длина волны λ задана.

1.17. Найти волновой вектор и скорость волны V. Волна описывается уравнением , где , и – постоянные.

1.18. Плоская волна с длиной λ распространяется вдоль направления, образующего с осями Х, Υ, Z углы π/3, π/4, и π/3 соответственно. Написать уравнение волны. Амплитуда и частота равны соответственно А и ν.

1.19. Доказать, что любая функция вида является решением волнового уравнения. Каков физический смысл постоянной ?

1.20. Плоская волна задана уравнением

где смещение частиц среды y задано в мкм, t в с, х в м. Найти отношение амплитуды смещения частиц среды к длине волны.

1.21. Плоская волна задана уравнением . Для момента времени t=0 изобразите графики зависимости от х величин у, ∂y/∂t и ∂y/∂x.

1.22. Две плоские синусоидальные волны, амплитуды которых одинаковы, а частоты соответственно n и n+∆n (∆n n2 > n1 (n1=1). Луч естественного света падает на границу воздух – стекло под углом Брюстера. За счет преломлений и отражений луч разделяется на несколько лучей. Какие из лучей (1÷6) будут полностью поляризованы?

2.52. При дифракции на щели минимум третьего порядка наблюдается при угле дифракции 45°. Какое общее количество минимумов можно наблюдать в дифракционной картине? Под каким углом будет наблюдаться последний минимум?

2.53. В опыте по наблюдению дифракции Френеля круглое отверстие открывает две зоны Френеля. Диафрагма с отверстием расположена на одинаковом расстоянии от точечного источника света и экрана. Между источником света и отверстием поставили собирающую линзу так, чтобы при этом источник света оказался в ее фокусе. Светлое или темное пятно будет наблюдаться в центре дифракционной картины?

2.54. На тонкую прозрачную пленку с показателем преломления n=1,33 по нормали к ее поверхности падает световой луч. При непрерывном изменении длины волны света обнаружили, что в отраженном луче за счет интерференции максимальное увеличение интенсивности наблюдается у лучей с длинами волн λ1=450 нм и λ2=750 нм. Найти толщину пленки.

2.55. Пучок естественного света падает на поляризатор, состоящий из N поляризационных пластинок. Плоскость поляризации каждой из пластинок повернута на 30° по часовой стрелке относительно плоскости поляризации предыдущей пластинки. Какая доля интенсивности падающего света пройдет через поляризатор? Поглощением света пренебречь.

2.56. Две когерентные световые волны, поляризованные во взаимно перпендикулярных плоскостях, имеют разность фаз ∆φ=π/3. Модули амплитуд векторов напряженности электрического поля волн одинаковы E1=E2=E0. В результате интерференции получили эллиптически поляризованный свет. Найти наибольшее и наименьшее значения модуля вектора напряженности электрического поля световой волны.

3. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВЫЕ СВОЙСТВА СВЕТА.

Поток энергии, испускаемый единицей площади поверхности нагретого тела по всем направлениям в пределах телесного угла 2π (энергетическая светимость тела Rm), равен

где – испускательная способность тела, – циклическая частота.

где Вт/м2К4 – постоянная Стефана – Больцмана;
T – температура.

Закон Кирхгофа: отношение испускательной способности тела к его поглощательной способности есть универсальная функция частоты и температуры f(ω,T). Испускательная способность абсолютно черного тела, описывается формулой Планка:

где – постоянная Планка; с – скорость света; k – постоянная Больцмана. При переходе от частоты к длине волны эта функция приобретает вид:

Испускательная способность абсолютно черного тела связана с равновесной плотностью энергии теплового излучения u(ω,T) соотношением

где – некоторая функция отношения частоты к температуре.

Для функции закон Вина имеет вид

где некоторая функция произведения (λ;T).

Закон смещения Вина:

где – длина волны, на которую приходится максимум функции ; b=2,898 (м·К) – постоянная Вина.

Уравнение Эйнштейна для фотоэффекта

где – частота света, – работа выхода электронов с поверхности жидкости или твердого тела, – кинетическая энергия вылетающих электронов.

Изменение длины волны рентгеновского излучения при рассеянии на свободном электроне (эффект Комптона)

где – длина волны рентгеновского излучения после рассеяния; – длина волны падающего излучения; – масса покоя электрона; – угол, под которым рассеивается излучение; – комптоновская длина волны.

Задача 1. Определить энергетическую светимость абсолютно черного тела в интервале длин волн =1 нм, соответствующую максимуму его испускательной способности при T=1000 К.

Решение. Из закона смещения Вина определим длину волны излучения абсолютно черного тела, на которую приходится максимум излучения.

м.

Интервал длин волн много меньше длины волны , поэтому энергетическую светимость можно определить как произведение испускательной способности на

Задача 2. На металлическую пластину падает свет с длиной волны λ=420 нм. Фототок прекращается при запирающем потенциале
U=0,95 В. Определить скорость выбиваемых электронов и работу выхода.

Решение. Скорость электронов найдем, воспользовавшись законом сохранения энергии mV2/2=eU, где е – заряд электрона. Скорость электрона:

м/с.

Работа выхода фотоэлектронов равна

Задача 3. В опыте Комптона угол рассеивания рентгеновских фотонов равен φ=90°. Энергия рассеянных фотонов Е=0,4 МэВ. Какова энергия фотонов до рассеивания? Какова энергия, импульс и скорость электронов отдачи?

Решение. Изменение длины волны в результате рассеяния на свободном электроне определяется с помощью формулы Комптона:

Длины волн выразим через энергии Е1 и Е0 соответствующих фотонов:

Отсюда следует, что энергия фотонов до рассеивания равна

Энергия покоя электрона m0c2=0,51 МэВ. Энергию фотона выразим в мегаэлектронвольтах:

МэВ.

Из закона сохранения энергии следует, что кинетическая энергия электрона отдачи равна разности энергии фотона до рассеяния и после рассеяния Ее=E0-E1=1,85–0,4=1,4 МэВ.

Импульс электрона найдем из закона сохранения импульса:

, где и — импульс фотона до рассеяния и после рассеяния. Векторная диаграмма импульсов при рассеянии изображена на рис.2. Из диаграммы следует, что

Импульс фотонов представим через их энергию, выраженную в джоулях,

кг·м/с.

Скорость электронов отдачи найдем, воспользовавшись выражением для релятивистского импульса

Отсюда следует, что

м/с.

3.1. Участок поверхности нагретого тела площадью ∆S за время τ излучает в пределах телесного угла 2π энергию ∆W. Какова энергетическая светимость этого участка?

3.2. Испускательная способность тела задана уравнением

0, ω ω2,

где b – постоянная, ω – частота излучения. Рассчитать энергетическую светимость тела.

3.3. Испускательная способность тела задана уравнением rω=roexp(—αω), где ro и α — постоянные. Определить энергетическую светимость тела.

3.4. На графике испускательной способности абсолютно черного тела выделены два узких участка, площади которых равны (рис. 3.1). Одинаковы ли на указанных частотах ω1 и ω2:
1) испускательная способность rω.т;
2) энергетическая светимость ∆Rω.Τ?

3.5. С помощью формулы Вина показать, что наиболее вероятная частота теплового излучения пропорциональна температуре ωвер

3.6. С помощью формулы Вина показать, что максимальная испускательная способность теплового излучения (rω)max

T5.
T – абсолютная температура.

3.7. С помощью формулы Планка показать, что в области, где hω >kT, для испускательной способности абсолютно черного тела справедлива формула Вина.

3.9. Найти соотношение между величинами rω.T. и rλ.T. Записать формулу Планка для величины rλ.T.

3.10. Вычислить с помощью формулы Планка энергетическую светимость абсолютно чёрного тела в интервале длин волн Δλ=1 нм, соответствующем максимуму испускательной способности при Т=3000 К.

3.11. С помощью формулы Планка показать, что максимальное значение испускательной способности абсолютно чёрного тела пропорционально абсолютной температуре в пятой степени:

3.12. С помощью формулы Планка показать, что длина волны, на которую приходится максимум испускательной способности чёрного тела, обратно пропорциональна температуре: λ0=b/T, где b – постоянная Вина.

3.13. Температура поверхности Солнца равна T0=5500 К. Принимая Солнце за абсолютно черное тело, оценить массу, теряемую им за секунду в результате излучения.

3.14. Для абсолютно черного тела вблизи его максимума испускательной способности рассчитать с помощью формулы Планка мощность излучения с единицы поверхности в интервале длин волн ∆λ=1 нм. Температура тела равна 4000 К.

3.15. Вблизи максимума испускательной способности Солнца рассчитать с помощью формулы Планка энергию, которую оно излучает с единицы поверхности в интервале длин волн ∆λ=1 нм. Температура Солнца T=5500 К. Считать, что Солнце обладает свойствами абсолютно черного тела.

3.16. В условиях задачи 3.15 рассчитать энергию, которую излучает Солнце с единицы поверхности в интервале длин волн λ≤λmax.

3.17. В условиях задачи 3.15 рассчитать энергию, которую излучает Солнце с единицы поверхности в интервале длин волн λ>λmax.

3.18. На экране получен спектр излучения положительного кратера вольфрамовой дуги, имеющего температуру 4000 К. Определить отношение мощностей, излучаемых кратером в интервалах длин волн от 695 до 705 нм (участок красного цвета) и от 395 до 405 нм (участок фиолетового цвета). Принять, что кратер излучает как черное тело а поглощение в стекле и воздухе одинаково для красных и фиолетовых лучей.

3.19. Для абсолютно чёрного тела в области максимума испускательной способности определить мощность излучения с 1 см2 его поверхности для интервала длин волн λ0,01λмах. Температура тела Т=2000 К.

3.20. Абсолютно чёрное тело имеет температуру t1=200 °С. Какова будет температура тела, если в результате нагревания поток излучения увеличился в 100 раз?

3.21. Как и во сколько раз изменится поток излучения абсолютно чёрного тела, если его максимум испускательной способности переместится из красной части видимого спектра λ1=700 нм в фиолетовую λ2=393,6 нм?

3.22. На 1 см2 земной поверхности падает в среднем около 8,4 Дж солнечной энергии в 1 мин. Расстояние от Земли до Солнца 1,5·1011 м, диаметр Солнца 1,39 109 м, температура Солнца 6000 К. Считая Солнце абсолютно чёрным телом, найти постоянную в законе Стефана-Больцмана.

3.23. Источником радиоизлучения Солнца в метровом диапазоне является его корона. Определить поток радиоизлучения от Солнца на Земле в полосе шириной Δω=1 МГц вблизи длины волны λ=1 м, предполагая, что это излучение является тепловым. Эффективная температура короны равна Т=106 К, эффективный радиус короны r=6,95·105 км, радиус земной орбиты R=1,5·108 км.

3.24. Металлический шар радиусом R=1 см и теплоемкостью C=14 Дж/К при температуре T=1200 К выброшен в межпланетное пространство. Коэффициент поглощения шара A=0,4. Через какое время температура шара уменьшится вдвое?

3.25. По пластинке длиной l=4 см и шириной b=0,5 см проходит электрический ток I=15 А. После установления теплового равновесия температура пластинки стала равной T=2000 К. Определить напряжение, подводимое к пластинке, если коэффициент поглощения пластинки А=0,6. Считать, что температура по всей площади пластинки постоянна, а все выделяющееся тепло теряется в результате излучения.

3.26. Удаленный от других тел медный шарик облучен электромагнитным излучением с длиной волны λ=140 нм. Определить его потенциал?

3.27. Небольшое идеальное отражающее зеркальце массой m=10 мг подвешено на нити длиной l=10 см. Найти угол, на который отклониться нить, если по нормали к зеркалу в горизонтальном направлении произвести «выстрел» импульсом лазерного излучения с энергией E=13 Дж.

3.28. Найти среднее давление лазерного импульса на поверхности тела. Длительность импульса τ=0,13 мс, средняя энергия импульса
W=10 Дж, диаметр пятна d=10 мкм. Свет падает по нормали к поверхности тела, коэффициент отражения которой =0,5.

3.29. Сколько фотонов попадает на 1 см2 поверхности Земли, перпендикулярной к солнечным лучам, за 1 мин? Солнечная постоянная ω≈1,4·103 Дж/(м2·с), средняя длина волны λср≈550 нм.

3.30. Точечный источник монохроматического света на длине волны λ=500 нм имеет мощность P=10 Вт. На каком максимальном расстоянии этот источник будет замечен человеком? Глаз человека реагирует на световой поток W=60 фотонов в секунду. Диаметр зрачка глаза человека d=0,5 см.

3.31. Параллельный пучок света с интенсивностью Io падает под углом φ на плоское зеркало с коэффициентом отражения ρ. Определить давление света на зеркало.

3.32. В сферическом сосуде, из которого откачан воздух, помещены два электрода из цинка. К ним подсоединён конденсатор ёмкостью c=3,5 мкФ (рис. 3.2.). Один из электродов освещается светом с длиной волны λ=0,25 мкм. Какой заряд будет находиться на конденсаторе при длительном освещении? Работа выхода электрона для цинка А=3,74 эВ.

3.33. На пластинку площадью S=8 см2 по нормали к ее поверхности падает излучение с плотностью энергии q=1 Вт/см2. Частота света ν=4,6·1015 с-1. Какой ток может быть снят с пластинки, если считать, что каждый фотон выбивает электрон?

3.34. Какой частоты нужно взять свет, чтобы выбитые из вольфрамового катода электроны задерживались на расстоянии 4 см в электрическом поле напряженностью 1,7 В/см?

3.35. Опыт показал, что задерживающее напряжение для фотоэлектронов равно 2 В. Электрод облучили светом с длиной волны
λ=200 нм. Найти красную границу фотоэффекта.

3.36. Частота падающего света в опыте Комптона равна 4·1018 Гц. Найти частоту света, отраженного под углом 120° к направлению его падения.

3.37. Длина волны падающего света в опыте Комптона равна λ. Найти длину волны отраженного света, если известно, что электрон отдачи полетел под углом α=60° к первоначальному направлению распространения света и обладал импульсом .

3.38. На площадь S=6 см2 по нормали падает монохроматический свет с плотностью потока энергии q=1,5 Вт/см2. Снятый с этой площади фототок насыщения равен 0,2 А. Считая, что каждый фотон выбивает электрон, найти частоту света и энергию фотона.

3.39. Фотоны с длиной волны 330 нм выбивают электроны, которые могут быть задержаны на расстоянии 2 см в электрическом поле напряженностью 2 В/см. Какова работа выхода электронов из металла
(в эВ)?

3.40. Фототок вызывается светом с длиной волны 400 нм. Красная граница фотоэффекта 800 нм. Найти запирающее напряжение для электронов.

3.41. Частота падающего света в опыте Комптона ν1=3·1022 1/с. Под каким углом рассеивается свет, если частота рассеянного света
ν2=2,5·1022 1/с?

3.42. Скорость фотоэлектронов равна 3·106 м/с. Найти задерживающую разность потенциалов и частоту падающего света. Работа выхода равна 4,5 эВ.

3.43. Найти красную границу фотоэффекта и построить график зависимости задерживающей разности потенциалов от частоты. При длине волны света 520 нм кинетическая энергия электронов равна 2 эВ.

3.44. В опыте Комптона угол рассеяния фотонов равен 180°. Длина волны падающих фотонов равна λ=0,5 нм. Найти частоту рассеянных фотонов.

3.45. При облучении катода фотоэлемента ток насыщения равен 0,01 А. Длина волны света равна 500 нм. Площадь катода 2 см2. Найти плотность потока энергии света.

3.46. Известно, что при освещении фотоэлемента светом с длиной волны λ1=400 нм вылетают электроны, которые могут быть задержаны запирающим напряжением U1=6 В. Каково, запирающее напряжение для электрона, выбитого светом с длиной волны λ2=650 нм?

3.47. Красная граница фотоэффекта для катода равна 900 нм. Построить график зависимости запирающего напряжения от частоты.

3.48. В эффекте Комптона найти изменение длины волны рентгеновского излучения. Угол рассеяния фотонов равен 120°, а их длина волны 0,5 нм.

3.49. Какая доля энергии фотона в эффекте Комптона приходится на электроны отдачи? Угол рассеяния для фотонов с энергией ε=0,6 МэВ равен φ=π/2.

3.50. В опыте Комптона угол рассеяния света изменился от 90° до 180°. Во сколько раз изменится сдвиг по длине волны в результате опыта?

3.51. Фотон с частотой ω0 испущен с поверхности звезды, масса которой М и радиус R0. Вычислить гравитационное смещение частоты фотона ∆ω/ω0 на очень большом расстоянии от звезды.

3.52. Два абсолютно черных шарика радиусами r1=4 см и r2=2 см, имеющие постоянные температуры T1=400 К и T2=800 К, находятся в вакууме на расстоянии d0=0,6 м. Между шариками помещена небольшая пластинка радиусом r0