Уравнение первой степени с называется уравнение вида ax by c (4 видео)

Линейное уравнение первой степени с двумя переменными

Линейное уравнение первой степени с двумя переменными.

Линейное уравнение первой степени с двумя переменными – это уравнение вида ax + by = c, где x и y – неизвестные, a, b, c – некоторые числа, при этом хотя бы одно из чисел a и b не равно нулю. Числа a и b называются коэффициентами при неизвестных, c – свободным членом.

Подобное определение не всегда сразу понятно, и, безусловно, требует дополнительных разъяснений. Попробуем объяснить.

Что означает уравнение с двумя переменными?

Тут все просто. Это уравнение, в котором присутствует сразу два неизвестных числа. Для какой задачи мы можем использовать подобную математическую модель? Например, в 7 Б классе учатся 18 человек. Причем неизвестно, сколько девочек и сколько мальчиков. Пусть мальчиков будет x, а девочек y. Таким образом, у нас получается такое уравнение:
x + y = 18. Заметим, что у нас много вариантов значений x и y, при которых наше уравнение обратится в верное числовое равенство. Например, x = 10, y = 8 или x = 5, y = 13 и т.д.

Такую пару чисел, при которой уравнение с двумя переменными обращается в верное равенство, называют решением уравнения. К примеру, x = 2 и y = 16 – решение уравнения x + y = 18. Это решение можно записать и в кратком виде — (2; 16). Важно при этом соблюдать порядок записи чисел. В уравнении вида ax + by = c решение записывается именно в таком порядке – (x; y). То есть сначала x, потом y.

Насколько много решений у уравнения с двумя переменными?

Обычно, если коэффициенты a и b не равны нулю, решений уравнения с двумя переменными бесконечное множество. Действительно, если подставлять в уравнение значения x, всегда можно будет определить соответствующее значение y, при котором уравнение обратится в верное равенство. Но бывает и такое, когда уравнение с двумя переменными не имеет решений. Такое возможно, когда, например, коэффициенты a и b равны нулю, а свободный член c ≠ 0.

Что означает уравнение первой степени?

Это означает что степень, в которую возводятся переменные этого уравнения – 1. То есть, у нас нет в уравнении переменных, которые мы возводим в квадрат, куб, четвертую степень, извлекаем корень и т.д.

Что означает линейное уравнение?

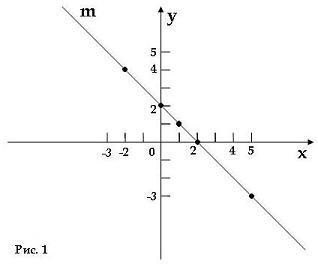
Линейное уравнение – это уравнение прямой линии. В этом легко убедиться, вспомнив понятие координатной плоскости. Мы знаем, что каждой паре чисел соответствует единственная точка на координатной плоскости. Теперь возьмем, к примеру, уравнение x + y = 2. Во множество решений данного уравнения попадают такие пары чисел: (0; 2), (2; 0), (1; 1), (5; -3), (-2; 4). Построим эти точки и проведем через них прямую m.

Мы получили график прямой m. Каждая точка этой прямой имеет координаты, являющиеся решением уравнения x + y = 2, или еще говорят, что каждая точка удовлетворяет уравнению x + y = 2. Вообще для того чтобы построить прямую, достаточно найти 2 пары чисел, удовлетворяющих линейному уравнению. И через точки с данными координатами можно строить прямую.

Содержание

Алгебра. 7 класс
Уравнение с двумя переменными
Уравнение с двумя переменными и его решение
Свойства уравнения с двумя переменными
Примеры
💡 Видео

Видео:Алгебра.7 класс (Урок№42 - Уравнения первой степени с одним неизвестным.)Скачать

Алгебра. 7 класс

Уравнения первой степени с двумя неизвестными

Математические термины

Стандартный вид

Определение

Значение переменной

Необходимо запомнить

Уравнение вида $ax + by =c$, где $x$ и $y$ – неизвестные и свободный член c – любые действительные числа, называется линейным уравнением с двумя неизвестными.

$ax + by =c$ – нормальный вид такого уравнения.

Каждая пара значений x и y, удовлетворяющая уравнению с двумя неизвестными, называется решением этого уравнения.

Линейное уравнение с двумя неизвестными обычно имеет бесконечное множество решений и поэтому называется неопределенным уравнением.

Если в уравнении первой степени с двумя неизвестными коэффициент при y равен нулю, то получим уравнение с одним неизвестным ($x$). Например:

Графиком последнего уравнения, а поэтому и двух других равносильных ему уравнений, является прямая, параллельная оси ординат.

Итак, графиком уравнения $ax + by = c$, если $a$ и $b$ не равны нулю одновременно, является прямая линия. Ее обычно строят по точкам пересечения с осями координат. Если $a = 0$ и $b = 0$, то возможны два случая:

1) $0x + 0y =17$ или $0 = 17$ – уравнение не имеет ни одного решения и ему не удовлетворяют координаты ни одной точки плоскости;

2) $0x + 0y = 0$ или $0 = 0$ – уравнение имеет бесчисленное множество решений (причём значения $x$ и $y$ здесь даже не зависят друг от друга) и ему удовлетворяют координаты всех точек плоскости.

Задача на составление неопределенного уравнения

Трёхногие инопланетяне выгуливают на лужайке своих двуногих питомцев. Кто-то подсчитал, сколько ног ходит по лужайке. Их оказалось $15$. Сколько было инопланетян и сколько их питомцев?

Необходимо ввести две переменные: $x$ – число инопланетян, $y$ – число питомцев, тогда получим уравнение $3x + 2y = 15$.

Давайте же узнаем сколько инопланетян выгуливало своих питомцев.

$3x + 2y = 15$. Выразим y через $x$: $y=frac$, далее воспользуемся методом перебора: при $x = 1$, $y = 6$, при $x = 2$, $y: notin : N$ , при $x = 3$, $y = 3$.

Ответ: $1$ инопланетянин и $6$ питомцев; $3$ инопланетянина и $3$ питомца.

Подобные уравнения встречаются часто, они-то и называются неопределенными. Особенность их состоит в том, что уравнение содержит две или более переменных и требуется найти все целые или натуральные их решения. Такими уравнениями и занимался Диофант. Он изобрел большое число способов решения подобных уравнений, поэтому их часто называют диофантовыми уравнениями.

Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

Уравнение с двумя переменными

Уравнение с двумя переменными и его решение

Уравнение вида ax+by = c , где a,b,c — данные числа, называется линейным уравнением с двумя переменными x и y.

Например: 2x+5y = 6; -x+1,5y = 0; $frac$ x-8y = 7

Уравнение с двумя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x и y.

Например: $2x^2+y^2 = 3, x-5y^2 = 1, 7x^3+y = 7$

Решением уравнения с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y=6 решениями являются пары

x = -2, y = 2; x = -1,y = 1,6; x = -3,y = 2,4 и т.д.

Уравнение имеет бесконечное множество решений.

Свойства уравнения с двумя переменными

Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными.

Уравнения с двумя переменными имеют такие же свойства, как и уравнения с одной переменной:

если в уравнении перенести слагаемое из одной части в другую и изменить его знак, получится уравнение, равносильное данному;
если обе части уравнения умножить или разделить на одно и то же, отличное от нуля число, то получится уравнение, равносильное данному.

Например: $2x+5y = 6 ⟺5y = -2x+6 iff y = -0,4x+1,2$