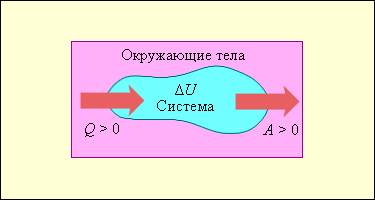
Уравнение первого закона термодинамики для неравновесных процессов (7 видео)

Первый закон термодинамики

На рисунке 3 . 9 . 1 условно проиллюстрированы энергетические потоки между выделенной термодинамической системой и окружающими телами. В случае, если тепловой поток направлен к термодинамической системе, то некоторая величина Q > 0 , если же система совершает положительную работу над окружающими ее объектами, то справедливо неравенство A > 0 .

Рисунок 3 . 9 . 1 . Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.

Состояние системы меняется, когда происходит процесс ее обмена теплом с окружающими объектами, и она совершает положительную или отрицательную работу. Изменяются макроскопические параметры системы, такие как температура, объем и давление. По причине того, что внутренняя энергия U всецело определяется макроскопическими параметрами, которые характеризуют состояние системы, процессы совершения работы и теплообмена провоцируют изменения внутренней энергии данной системы Δ U .

Содержание

Определение 1 -го закона термодинамики
Первый закон термодинамики в процессах газов
Первое начало термодинамики: основные положения
Формулировки первого начала термодинамики
Готовые работы на аналогичную тему
Частные случаи применения первого начала термодинамики
Первое начало термодинамики для неравновесных процессов
термодинамика неравновесных процессов
📺 Видео

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Определение 1 -го закона термодинамики

Первый закон термодинамики представляет собой некое обобщение закона сохранения и превращения энергии для термодинамической системы, и формулируется следующим образом:

Изменение Δ U внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q , переданной системе, и работой A , совершенной системой над внешними телами.

Формула первого закона термодинамики, зачастую записывается в ином виде:

Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.

Первый закон термодинамики представляет из себя, по сути, обобщение опытных фактов. Если руководствоваться им, то можно заявить, что энергия не возникает и не исчезает бесследно, а передается от одной системы к другой, меняя свои формы. Невозможность создания вечного двигателя (perpetuum mobile) первого рода, то есть машины, которая может совершать полезную работу, не потребляя энергию извне и не претерпевая каких-либо изменений во внутренней конструкции агрегата, являлась важным следствием первого закона термодинамики. В подтверждение этого выступает тот факт, что каждая из огромного множества попыток создания такого устройства неизменно заканчивалась неудачей. Реальная машина может совершать положительную работу A над внешними объектами, только получая некоторое количество теплоты Q от окружающих тел или уменьшая Δ U своей внутренней энергии.

Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Первый закон термодинамики в процессах газов

Первый закон термодинамики может применяться к изопроцессам в газах.

В изохорном процессе, то есть в условиях неизменного объема ( V = c o n s t ) , газ не совершает работы, A = 0 .

В этом случае справедливой будет формула внутренней энергии газа:

Q = ∆ U = U ( T 2 ) — U ( T 1 ) .

В данном выражении U ( T 1 ) и U ( T 2 ) представляют внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит лишь от температуры, что исходит из закона Джоуля. При изохорном нагревании газ поглощает тепло ( Q > 0 ) , чем провоцирует увеличение его внутренней энергии. В условиях охлаждения тепло отдается внешним объектам ( Q 0 ) .

В изобарном процессе, предполагающем постоянность значения давления ( p = c o n s t ) , работа, совершаемая газом, выражается в виде соотношения:

A = p ( V 2 — V 1 ) = p ∆ V .

Первый закон термодинамики для изобарного процесса дает:

Q = U ( T 2 ) — U ( T 1 ) + p ( V 2 — V 1 ) = ∆ U + p ∆ V .

При изобарном расширении Q > 0 тепло поглощается газом, и он совершает положительную работу. При изобарном сжатии Q 0 тепло переходит внешним телам. В таком случае A 0 . При изобарном сжатии уменьшаются температура газа T 2 T 1 и значение внутренней энергии Δ U 0 .

В изотермическом процессе температура газа не меняет своей величины, следовательно, не изменяется и внутренняя энергия газа, Δ U = 0 .

Первый закон термодинамики для изотермического процесса выражается соотношением

Теплота Q , приобретенная газом в процессе изотермического расширения, превращается в работу, совершаемую над внешними объектами. И наоборот, изотермическое сжатие приводит к преобразованию уже работы внешних сил, произведенной над газом, в передающееся окружающим телам тепло.

Вместе с изохорным, изотермическим и изобарным процессами в термодинамике нередко исследуют процессы, происходящие в условиях отсутствующего теплообмена с окружающими объектами.

Адиабатическая оболочка – это сосуд с теплонепроницаемыми стенками.

Процессы сжатия или расширения газа в подобных емкостях называют адиабатическими.

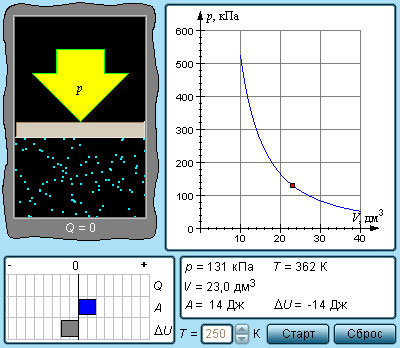
Рисунок 3 . 9 . 2 . Модель адиабатического процесса.

В адиабатическом процессе Q = 0 . По данной причине первый закон термодинамики принимает вид:

Выходит, что газ производит работу за счет падения значения его внутренней энергии.

Расширение или сжатие газа на плоскости p , V проиллюстрирована кривой, называемой адиабатой.

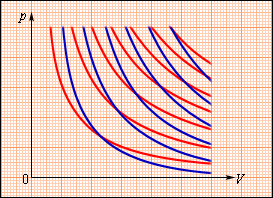
В процессе адиабатического расширения газом совершается положительная работа A > 0 , что является причиной понижения значения внутренней энергии Δ U 0 . Данное явление провоцирует падение его температуры. Исходя из этого, можно заявить, что величина давления газа при адиабатическом расширении понижается быстрее, чем это происходит в изотермическом (рис. 3 . 9 . 3 ).

Рисунок 3 . 9 . 3 . Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа.

В условиях координат ( p , V ) выводящееся в термодинамике уравнение адиабатического процесса для идеального газа принимает следующий вид:

p V γ = c o n s t .

Данное выражение, в котором γ = C p C V – показатель адиабаты, C p и C V – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом, называется уравнением Пуассона. В условиях одноатомного газа γ = 5 3 = 1 , 67 , двухатомного γ = 7 5 = 1 , 4 , многоатомного γ = 1 , 33 .

Работа газа в адиабатическом процессе выражается через температуры начального T 1 и конечного T 2 состояний и принимает вид:

A = C V ( T 2 — T 1 )

Адиабатический процесс относится к изопроцессам.

В термодинамике важное место занимает физическая величина, называемая энтропией. Изменение энтропии в том или ином квазистатическом процессе эквивалентно некоторому обретенному системой теплу Δ Q T . Так как на каждом участке адиабатического процесса Δ Q = 0 , энтропия в нем не претерпевает изменений.

Любые изопроцессы, в том числе и адиабатические, являются квазистатическими. Промежуточные состояния газа в таких процессах близки к состояниям термодинамического равновесия. Каждая точка, принадлежащая адиабате, описывает равновесное состояние. Однако, процесс, который проводится в адиабатической оболочке, то есть при отсутствующем теплообмене с окружающими объектами, не обязательно удовлетворяет данному условию.

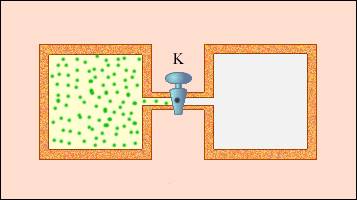
Примером неквазистатического процесса, в котором промежуточные состояния не находятся в состоянии равновесия, служит расширение газа в пустоту. На рисунке 3 . 9 . 3 иллюстрируется жесткая адиабатическая оболочка, состоящая из двух разделенных вентилем K сообщающихся емкостей. В изначальном состоянии газом заполнен один из сосудов, в это же время во втором находится лишь вакуум. Открытие вентиля запускает процесс расширения газа. Он заполняет оба сосуда, и устанавливается новое равновесное состояние.

В таком процессе Q = 0 , по той причине, что исключен теплообмен с окружающими телами, и A = 0 , так как оболочка недеформируема. Первый закон термодинамики позволяет сказать, что Δ U = 0 , то есть внутренняя энергия газа не претерпела никаких изменений. Так как внутренняя энергия идеального газа зависит лишь от температуры, температура газа в начальном и конечном состояниях одинакова. Изображающие эти состояния точки на плоскости ( p , V ) лежат на одной изотерме. Все промежуточные состояния газа не являются равновесными и не могут быть изображены на диаграмме.

Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.

Рисунок 3 . 9 . 4 . Расширение газа в пустоту.

Видео:Первый закон термодинамики. 10 класс.Скачать

Первое начало термодинамики: основные положения

Вы будете перенаправлены на Автор24

Первое начало термодинамики сформулировано в середине 19 в. Оно стало результатом научных работ:

немецкого физика Ю. Майера, который распространил закон о сохранении механической энергии первоначально на термические (1842 г.), а впоследствии (1845 г.) и на все немеханические явления;
английского физика Дж. Джоуля (1843 г.), экспериментальным путем обосновавшего новый закон;
немецкого физика Г. Гельмгольца (1847 г.), распространившего закон сохранения энергии на все ее разновидности.

Первое начало термодинамике в виде закона о сохранении (уравнения баланса энергии) стандартно используется в:

термодинамике потока.
неравновесной термодинамике.

В равновесной термодинамике под первым законом зачастую подразумевается одно из следствий закона о сохранении энергии. Следствием этого становится факт отсутствия единой формулировки первого начала термодинамики, которые используются в научной и учебной литературе. Наиболее удачными считаются формулировки Кирхгофа и Гиббса.

Видео:Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Формулировки первого начала термодинамики

Первое начало термодинамики в стандартной формулировке характеризуется невозможностью существования в физической реальности вечного двигателя первого рода, который мог бы совершать работу без энергии извне. Поступающей от какого-либо источника.

Согласно формулировке Кирхгофа, существует функция состояния $U$, называемая внутренней энергией. Она представляет собой часть полной энергии системы, при изменении которой в любом процессе в закрытой системе получится сумма теплоты и работы. Каждое состояние термодинамической системы при этом характеризуется конкретным значением $U$ в независимости от того, каким способом данная система приводится в рассматриваемое состояние.

Таким образом, те составные части в полной энергии системы, которые неизменны в изучаемом процессе, не входят во внутреннюю энергию системы. Как следствие — внутренняя энергия представляет изменяемую часть полной энергии системы.

Готовые работы на аналогичную тему

Традиционно теплота и работа трактуются как формы энергопередачи, они характеризуются описательными дефинициями. Внутренняя энергия в формулировке Кирхгофа выступает функцией состояния и привязана к функциям процесса (работе и теплоте). Фактически это означает, что она привязана равновесным процессам, происходящим в закрытых системах.

К обобщенным термодинамическим координатам не будет относиться ни масса системы, ни количество составляющих ее веществ. В традиционном подходе к обоснованию термодинамики, массы веществ по этой причине не включены в перечень переменных, от которых будет зависеть внутренняя энергия.

Для открытых систем переменного состава (в химической термодинамике) первое начало формулируется как аксиома о существовании внутренней энергии в формате функции состояния, в постулируемые свойства которой входит ее функциональная зависимость от массы составляющих систему веществ. К. Каратеодори первое начало термодинамики выразил в виде утверждения о существовании внутренней энергии в формате составной части полной энергии системы. Внутренняя энергия в формулировке ученого не представляет характеристическую функцию собственных независимых переменных.

Для открытой системы оказываются беспредметными классическая точка зрения (об эквивалентности теплоты и работы) и позиция Каратеодори (при определении теплоты). При формальном распространении дефиниции Кирхгофа на внутреннюю энергию для открытых систем переменного состава, в выражение дефиниции добавляется еще одно слагаемое (энергия перераспределения масс веществ, составляющих систему) — $z$. Тогда:

Работа и теплота представляют в термодинамике независимо измеряемые величины. Наряду с тем, в традиционном подходе к построению принципов термодинамики отсутствуют способы для независимого измерения химической работы.

В своей научной работе в 1875 г. Дж. Гиббс пишет о равновесии гетерогенных веществ, рассматривая в термодинамике простых открытых систем внутреннюю энергию в качестве функции энтропии $S$, объема $V$ и масс веществ, составляющих систему: $m_1$, $m_2$, $m_i$.

Видео:Физики 10 класс Следствия первого закона термодинамики для различных процессовСкачать

Частные случаи применения первого начала термодинамики

Если $q=0$, система не производит обмен теплотой с окружающей средой или пребывает в состоянии стационарного теплообмена. Если потоки энергии отсутствуют, (когда $q=0$) выполнение системой работы $w$ способствует тому, что энергия системы $U$ убывает.

Ограниченность запаса внутренней энергии $U$ приводит к тому, что процесс, в котором системой долгое время выполняется работа (без поступления энергии извне) становится невозможным. Это запрещает существование вечных двигателей первого порядка. Первое начало термодинамики:

при циклическом процессе $Delta U=0$

в термодинамической знаковой системе: $W=-Q$

в теплотехнической знаковой системе: $W=Q$

при изобарном процессе $Q=Delta U+W=Delta U+pDelta V$

при изохорном процессе $W=0$

при изотермическом процессе: $Delta U=0$

Видео:Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Первое начало термодинамики для неравновесных процессов

Выражения первого начала классической термодинамики будут действительными только для обратимых процессов. Данное обстоятельство существенно ограничивает возможности дальнейшего развития принципов и практических приложений расчетных уравнений в классической термодинамике.

В связи с тем, что все реальные процессы необратимы, в физике вводится такое понятие, как «эффективная работа», представляющая разность термодинамической работы и необратимых потерь.

Работа, которая была потеряна в необратимых процессах (при трении, неравновесном теплообмене и пр.), превращается в тепло внутреннего теплообмена для тела. Такое тепло будет возвращаться рассматриваемому телу или передаваться телам внешней системы.

При этом уменьшится итоговая величина подвода тепла извне. Полное количество тепла, которое получает тело, будет характеризовать его термодинамический (приведённый) теплообмен.

Видео:2 1 Первый закон термодинамики ЭнтальпияСкачать

термодинамика неравновесных процессов

ТЕРМОДИНАМИКА НЕРАВНОВЕСНЫХ ПРОЦЕССОВ -общая теория макроскопич. описания термодинамически неравновесных процессов. Её наз, также н е р а вн о в е с н о й т е р м о д и н а м и к о й или т ер м о д и н а м и к о й н е о б р а т и м ы х п р о ц е с с о в.

Впервые термодинамич, соображения были применены к необратимым процессам В. Томсоном (Кельвином) в 1854. Последоват. изучение неравновесных процессов термодинамич. методами началось с работ Л. Онсагера, установившего в 1931 соотношения взаимности для коэф. феноменологич. законов, к-рым подчиняются необратимые процессы. Как самостоят. наука Т. н. п. стала развиваться в работах Дж. Мейкснера, И. Пригожина и С. де Гроота.

Классич. термодинамика даёт полное количеств. описание равновесных (обратимых) процессов, поэтому её иногда называют термостатикой. Для неравновесных процессов она устанавливает лишь неравенства, к-рые указывают направление этих процессов (напр., Клаузиуса неравенство). Осн. задача Т. н. п.- количеств. изучение неравновесных процессов для. состояний, не сильно отличающихся от равновесных, в частности определение скоростей неравновесных процессов в зависимости от внеш. условий. В Т. н. п. системы, в к-рых протекают неравновесные процессы, рассматривают как непрерывные среды, а их параметры состояния-как полевые переменные, т. е. непрерывные ф-ции координат и времени. Для макроскопич. описания неравновесных процессов систему представляют состоящей из элементарных объёмов (физически бесконечно малых элементов среды), к-рые всё же настолько велики, что содержат очень большое число частиц. Состояние каждого выделенного элемента среды характеризуется темп-рой, плотностью, хим. потенциалами и др. термодинамич. параметрами, зависящими от координат и времени. Количеств. описание неравновесных процессов заключается в составлении ур-ний баланса для элементарных объёмов на основе законов сохранения массы, энергии и импульса, а также ур-ния баланса энтропии и феноменологич. ур-ний для рассматриваемых процессов, выражающих потоки массы, импульса и энергии через градиенты термодинамич. параметров. Методы Т. н. п. позволяют сформулировать для неравновесных процессов первое и второе начала термодинамики в локальной форме (в зависимости от положения элемента среды), получить из общих принципов, не рассматривая деталей взаимодействия частиц, полную систему ур-ний переноса, т. е. ур-ния гидродинамики, теплопроводности и диффузии для простых и сложных систем (с хим. реакциями между компонентами, с учётом эл—магн. полей и др. факторов).

Законы сохранения. Для многокомпонентной системы поток массы в элемент объёма равен r k u k , где r k -плотность, u k -массовая скорость потока частиц данного вида; следовательно, з а к о н с о х р а н е н и я м а с с ы k-гo компонента имеет вид

Для суммарной плотности закон сохранения имеет вид дr/дt= — div(ru), где u — гидродинамич., или массовая, скорость среды (ср. скорость переноса массы), зависящая от координат и времени. Для концентрации к—л. компонента c k =r k /r закон сохранения массы имеет вид где J k = r k (u k —u) — диффузионный поток, d/dt = д/дt + (ugrad) — полная, или субстанциональная, производная по времени.

Изменение импульса элементарного объёма может происходить за счёт движения частиц, внутр. напряжений в среде P ab и внеш. сил F k , действующих на единицу массы k-гo компонента. З а к о н с о х р а н е н и я и м п у л ь с а, применённый к элементарному объёму среды, позволяет получить осн. ур-ния гидродинамики (Навье — Стокса уравнения):

где u a — декартовы компоненты скорости u, P ab =pd ab + p ab — тензор напряжений, р-давление, d ab — символ Кронекера, p ab — тензор вязких напряжений. З а к о н с о х р а н е н и я э н е р г и и для элементарных объёмов представляет собой первое начало термодинамики в Т. н. п. Плотность полной энергии складывается из плотности кинетич. энергии ru 2 /2, плотности потенц. энергии и плотности внутр. энергии ru (энергии теплового движения частиц и энергии их короткодействующих взаимодействий). Для рм из закона сохранения энергии получается ур-ние баланса (первое начало термодинамики в Т. н. п.):

где J q — поток тепла, -работа внутр. напряжений, — работа внеш. сил. Следовательно, внутр. энергия рм не сохраняется, сохраняется лишь полная энергия.

Уравнение баланса энтропии. Второе начало термодинамики в Т.н.п. выражает баланс энтропии (s — плотность энтропии на единицу массы) вследствие поступления потока энтропии J s,полн из окружающей среды и возникновения её в самой системе вследствие необратимых процессов с интенсивностью источника s (локальное производство на единицу объёма в единицу времени):

s>=0, dW — элемент поверхности системы. Отсюда следует ур-ние баланса энтропии в дифференц. форме:

Если имеют место необратимые процессы, s > 0, энтропия (в отличие от массы, энергии и импульса) не сохраняется. В Т. н. п. принимают, что уд. энтропия s является такой же ф-цией внутр. энергии и, уд. объёма w=1/r и концентраций c k , как и в состоянии полного термодинамич. равновесия, и, следовательно, для неё справедливы обычные термодинамич. равенства (г и п о т е з а л о к а л ь н о г о р а в н о в е с и я). Эту же гипотезу используют и в неравновесной статистич. термодинамике. Предполагают, что термодинамич, ф-ла остаётся справедливой и для элемента массы вдоль траектории его центра масс:

где все производные во времени являются полными.

Для плотности потока энтропии получается выражение, зависящее от плотности потока тепла J q и плотности потока диффузии J k :

а для локального производства энтропии — выражение, зависящее от потоков и градиентов термодинамич. параметров:

Т.о., локальное производство энтропии вызывается необратимыми процессами теплопроводности, диффузии и вязкости. В системах с хим. реакциями появляется ещё один член, связанный с хим. сродством реакций.

Положительность локального производства энтропии (s>0), очевидная из ф-лы (*), выражает в Т.н.п. закон возрастания энтропии (второе начало термодинамики). Возможное изменение плотности энтропии вследствие втекания её в элемент объёма или вытекания из него не связано с необратимыми процессами и может иметь любой знак. Интегрирование ур-ния баланса энтропии по объёму системы с учётом (*) даёт для полной энтропии S соотношение , эквивалентное теореме Карно — Клаузиуса.

Локальное производство энтропии (*) представляет собой сумму произведений потоков (напр., диффуз. потока J k , теплового потока J q , тензора вязких напряжений p ab ) и сопряжённых им термодинамич. сил Х i :

Термодинамич. силы Х i пропорц. градиентам термодинамич. параметров, вызывающим неравновесные процессы. Величины J i , X i могут быть векторами (теплопроводность и диффузия), тензорами (сдвиговая вязкость), скалярами (объёмная вязкость, скорость хим. реакции). Поэтому со-ответств. процессы наз. векторными, тензорными или скалярными.

Феноменологические уравнения. В Т. н. п. исходят из того, что при малых отклонениях системы от термодинамич. равновесия возникающие потоки линейно зависят от термодинамич. сил и описываются феноменологич. ур-ниями типа L ik — (феноменологич.) кинетические коэффициенты, или коэф. переноса (их наз. также онсаге-ровскими кинетич. коэф.). В прямых процессах термодинамич. сила X k вызывает поток J k , напр. градиент темп-ры вызывает поток теплоты (теплопроводность), градиент концентрации — поток вещества (диффузию), градиент скорости- поток импульса (к-рый определяет вязкость ),электрич. поле — электрич. ток (электропроводность ).Такие процессы характеризуются онсагеровскими кинетич. коэф., L ii >0, пропорц. коэф. теплопроводности, диффузии, вязкости, электропроводности, к-рые также наз. кинетич. коэф. или коэф. переноса. Термодинамич. сила X k может вызывать поток J i и при ik, напр. градиент темп-ры может вызывать поток вещества в многокомпонентных системах (термодиффузия ,или С о р е э ф ф е к т), а градиент концентрации — поток теплоты (диффузионный термоэффект, или Дюфура эффект ).Такие процессы наз. п е р ек р ё с т н ы м и или налагающимися эффектами; они характеризуются коэф, L ik при ik. С учётом феноменологич. ур-ний производство энтропии

В стационарном состоянии величина s минимальна при заданных внеш. условиях, препятствующих достижению равновесия (Пригожина теорема ).В состоянии термодинамич. равновесия s = 0.

Одна из осн. теорем Т. н. п.- Онсагера теорема взаимности, связанная с инвариантностью ур-ний движения относительно обращения времени, согласно к-рой в отсутствие магн. поля и вращения системы как целого онсагеров-ские кинетич. коэф. для потоков одинаковой чётности симметричны: L ik = L ki . Если на систему действует внеш. магн. поле Н или она вращается с угл. скоростью w, то

Это связано с тем, что силы Лоренца и Кориолиса не изменяются при изменении скоростей всех частиц на обратные лишь в том случае, если одновременно меняется на противоположное направление магн. поля или скорости вращения (см. Онсагера теорема).

При определ. свойствах пространственной симметрии системы феноменологич. ур-ний упрощаются. Напр., в изотропной системе потока и термодинамич. силы, имеющие разную тензорную размерность, не могут быть связаны между собой (частный случай Кюри принципа в Т.н. п.). Поэтому в производство энтропии могут входить произведения потоков и термодинамич. сил лишь одинаковой тензорной размерности: скаляры, полярные векторы, аксиальные векторы, симметричные тензоры с нулевым следом.

С учётом принципа Кюри и соотношений Онсагера Т. н. п. даёт для потока тепла J q и потока J 1 массы первой компоненты в бинарной (п = 2 )смеси феноменологич. ур-ния

Вместо феноменологич. коэф. L qq . L 11 , L 1q можно ввести коэф. теплопроводности l=L qq /T 2 , коэф. диффузии D·=L 11 m 11 /rc 2 T, коэф. термодиффузии D’ = L 1q /rc 1 c 2 T 2 , коэф. Дюфура D» = D’.

В случае вязкого течения изотропной жидкости феноменологич. ур-ние для тензора вязких напряжений имеет вид

h-сдвиговая вязкость, z — объёмная вязкость, d ab — символ Кронекера.

Т. н. п. позволяет описать неравновесные процессы в прерывных системах, напр. перенос тепла и массы между резервуарами, связанными капилляром, пористой стенкой или мембраной, если можно пренебречь объёмом капилляра или пор. В этом случае термодинамич. параметры меняются скачком. Если ввести приведённые величины:

поток тепла (где j u — изменение внутр. энергии, h k — уд. энтальпия), потоки диффузии j k =j k -c k j n /c n , (k= 1, 2, . n— 1), объёмный поток то они пропорц. термодинамич. силам — конечным разностям D T/T 2 , ( D ,m m ) T,p /T, Dр/Т, и феноменологич. ур-ния имеют вид:

Эти ур-ния описывают эффект термомолекулярного давления- возникновение конечной величины Dp/DT при j q = 0, j w = 0, термоэффузию — возникновение разности концентраций Dс k /DT при j q =0, j w = 0, механокалорич. эффект — существование стационарного состояния с переносом тепла при DT=0 и фиксированном перепаде давления Dр (при j k = 0). Т.н.п. прерывных систем позволяет описать также осмотическое давление (см. Осмос)и электрокинетические явления.

Т. н. п. используют для объяснения мн. неравновесных явлений в проводниках, напр, термоэлектрических явлений, гальваномагнитных явлений, термогальваномагнит-ных явлений. Она даёт теоретич. основу для исследования открытых систем.

Вывод законов Т. н. п. из законов механики (классич. и квантовой) и получение выражений для кинетич. коэф, через параметры, характеризующие строение вещества, входят в задачу н е р а в н о в е с н о й с т а т и с т и ч е с к о й т е р м о д и н а м и к и, к-рая относится к Т. н.п. так же, как статистич. термодинамика к термодинамике (см., напр., Грuнa — Кубо формулы). Обоснование Т.н. п. для газов даёт кинетическая теория газов.

Лит.: Пригожин И., Введение в термодинамику необратимых процессов, пер, с англ., М., 1960; Термодинамика необратимых процессов, пер. с англ., М., 1962; де Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964; Хаазе Р., Термодинамика необратимых, процессов, пер. с нем., М., 1967; Зубарев Д. Н., Неравновесная статистическая термодинамика, М.. 1971; Дьярмати И., Неравновесная термодинамика. Теория поля и вариационные принципы, пер. с англ., М., 1974; К айзер Д., Статистическая термодинамика неравновесных процессов, пер. с англ., М., 1990. Д. Н. Зубарев.