Уравнение перемещения балки при изгибе

Видео:Определение перемещений в балке. Метод сил. Правило Верещагина. СопроматСкачать

Виды перемещений при изгибе

Упругая линия балки – ось балки после деформации.

Прогиб балки $y$ – поступательное перемещение центра тяжести в поперечном направлении балки. Прогиб вверх считаем положительным, вниз – ’ емким.

Уравнение упругой линии – математическая запись зависимости $y(x)$ (прогиба по длине балки).

Стрела прогиба $f = <y_>$ – максимальное по длине значение прогиба балки.

Угол поворота сечения $varphi $ – угол, на который поворачивается сечение в процессе деформирования балки. Угол поворота считаем положительным, если сечение поворачивается против часовой стрелки, и наоборот.

Угол поворота сечения равен углу наклона упругой линии. Таким образом, функция изменения угла поворота по длине балки равна первой производной от функции прогибов $varphi (x) = y'(x)$.

Таким образом, при изгибе рассматриваем два вида перемещений – прогиб и угол поворота сечения.

Видео:Перемещения при изгибе. Часть 1. Дифференциальное уравнение изогнутой оси бруса.Скачать

Цель определения перемещений

Перемещение в стержневых системах (в частности в балках) определяются для обеспечения условий жесткости (прогибы ограничиваются строительными нормами).

Кроме этого, определение перемещений необходимо для расчета прочности статически невыдающихся систем.

Видео:Перемещения в балке при изгибе. МНП. Определение перемещ. в хар. точках балки (продолжение)Скачать

Дифференциальное уравнение упругой линии (изогнутой оси) балки

На данном этапе необходимо установить зависимость перемещений в балке от внешних нагрузок, способа закрепления, размеров балки и материала. Для полного решения задачи необходимо получить функцию прогибов $y(x)$ по всей длине балки. Вполне очевидно, что перемещения в балке зависят от деформаций каждого сечения. Ранее нами была получена зависимость кривизны сечения балки от изгибающего момента, действующего в этом сечении.

Кривизна линии определяется ее уравнением $y(x)$ так

где $y’$ и $y$ – соответственно, первая и вторая производная от функции прогибов с координатой x.

С практической точки зрения эту запись можно упростить. На самом деле $y’ = varphi $ – угол поворота сечения в реальных конструкциях не может быть большим, как правило не больше 1град = 0,017рад . Тогда $1 + <left( right)^2> = 1 + = 1.000289 approx 1$, то есть можно считать, что $frac = y» = frac<<y>><<d>>$. Таким образом, мы получили уравнение упругой линии балки (дифференциальное уравнение изогнутой оси балки). Это уравнение впервые получено Эйлером.

Получена дифференциальная зависимость показывает взаимосвязи между перемещениями и внутренними усилиями в балках. Учитывая дифференциальную зависимость между поперечной силой, изгибающим моментом и поперечной нагрузкой, покажем содержание производных от функции прогибов.

$y(x)$ – функция прогибов;

$y'(x) = varphi (x)$ – функция углов поворота;

$EI cdot y»(x) = M(x)$ – функция изменения изгибающего момента;

$EI cdot y»‘(x) = M'(x) = Q(x)$ – функция изменения поперечной силы;

$EI cdot <y^>(x) = M»(x) = q(x)$ – функция изменения поперечной нагрузки.

Видео:Перемещения в балке при изгибе. Дифференциальные зависимости для построения эпюр перемещенийСкачать

Расчет прогиба балки методом начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Видео:Определение перемещений в балке. Метод сил. Интеграл Мора. СопроматСкачать

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

• E – модуль упругости;
• I – момент инерции;
• V_k – прогиб сечения K;
• V_O – прогиб сечения O;
• θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_k, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, V O и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть V_O=0 и θ_O=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах .

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Видео:Построение эпюры прогибов балкиСкачать

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10 5 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см 4 ). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб V_O и угол поворота этого сечения — θ_O:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Видео:Метод начальных параметров Расчет перемещений сечений балкиСкачать

ПроСопромат.ру

Видео:Понимание напряжений в балкахСкачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Архив рубрики: Определение перемещений

Видео:Перемещения в балке при изгибе. Метод начальных параметров. Составление выражений для φ(х) и v(х).Скачать

Определение перемещений по формуле Симпсона

Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение .

1. Определим опорные реакции.

Наносим значение опорных реакций на расчетную схему

2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру М_F.

Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.

Строим эпюру М_F от заданной нагрузки.

3. Подберем сечение из двух швеллеров:

Подбираем 2 швеллера №33 см 3 .

Проверим прочность подобранного сечения.

Прочность обеспечена.

4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент .

Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.

Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп , определяем в ней необходимые ординаты. (рис. в).

Ординаты эп.М_F – все положительные, эп. – тоже.

Перемещения будем определять методом Мора по формуле Симпсона.

Определим момент инерции I_х для сечения.

Модуль продольной упругости Е для Ст3 Е = 2·10 5 МПа = 2·10 8 кПа. Тогда:

Угол поворота φ_А получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.

Определим угол поворота φ_В. (рис.г,д )

Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. от единичной силы (рис.ж).

Рассмотрим рис. е.

Строим эп. :

Определим прогиб в т. С.

Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).

(знак «— « говорит о том, что реакция R_А направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).

Строим эп. ,

Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.

Определим прогиб в точке С.

(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)

Аналогично определим линейное и угловое перемещения в т. D.

Определим у_D . (рис. к).

Строим эп. (рис.л) :

Определим φ_D (рис. м):

Строим эп. — (рис.н).

Определим угол поворота:

(угол поворота направлен в сторону, противоположную единичному моменту).

Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).

Проверим жесткость балки , где f – максимальный прогиб.

Максимальный прогиб — жесткость не обеспечена.

Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.

Видео:Перемещения при изгибе. Часть 2. Непосредственное интегрирование уравнения изогнутой осиСкачать

Интеграл Мора

Для решения вопросов жесткости элементов требуется определять перемещения (линейные, угловые). Существуют несколько способов определения перемещений, одним из которых является определение перемещений по интегралу Мора.

Алгоритм вычисления перемещений по интегралу (формуле) Мора:

1. Составляем выражение изгибающего момента M_F от действующей нагрузки.

2. Снимаем с балки (рамы, фермы и т.д.) все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент (если определяем угловое перемещение) по направлению искомого перемещения. Составляем выражение изгибающего момента от единичного фактора.

3. Подставляем выражения моментов в интеграл Мора:

где: Δ — перемещение в общем виде, знак Σ распространяется на все участки балки; EI – изгибная жесткость на участке.

Видео:Перемещения при изгибе. Общие понятия. Вывод ур-я изогнутой оси в форме метода нач. параметров.Скачать

Определение обощенных сил и перемещений

Потенциальную энергию можно определять через работу внешних сил (см. — здесь).

В общем случае: , где Р₀ – любой силовой фактор (растягивающая сила, крутящий момент и тому подобное) называется обобщённой силой;

δ₀ – соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением.

Под обобщённой силой Р₀ следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.

Рассмотрим общий случай нагружения при изгибе.

За отдельные обобщенные силы здесь можно принимать:

1) Сосредоточенную силу Р с реакциями и

2) Два момента М₀ с соответствующими реакциями.

3) Равномерно распределённую нагрузку q с реакциями А и В.

Обобщённым перемещением δ₀ будем называть величину, характеризующую деформацию, на которую нужно умножить обобщённую силу, чтобы подсчитать произведённую ею работу.

Обобщённым перемещением будут:

1) Прогиб f под силой P,

2) Взаимный угол поворота сечений, где приложены моменты М₀ :

3) Площадь, заключённая между первоначальной и изогнутой осью балки в районе расположения распределённой нагрузки:

Следует отметить, что если действующая на конструкцию нагрузка представлена несколькими обобщёнными силами (Р₀₁, P₀₂, P₀₃,… и т. д.),то каждое из обобщённых перемещений (δ₀₁, δ₀₂, δ₀₃ и т. д.) является, вообще говоря, функцией всех обобщённых сил:

Так, прогиб под силой Р (см. рисунок) является результатом действия не только силы Р , но и моментов М₀ и распределённой нагрузки q.

Обобщённое перемещение будем считать положительным, если соответствующая обобщённая сила на этом перемещении совершает положительную работу.

Обобщённое перемещение, соответствующее определённой обобщённой силе, не изменится при изменении способа закрепления элемента конструкции.

Зависимости могут быть записаны так:

Здесь а₁₁, а₂₁ и т. д. – некоторые коэффициенты пропорциональности.

Первый индекс указывает порядковый номер перемещения, второй – порядковый номер обобщённой силы.

Потенциальная энергия деформации, создающаяся в упругой системе в результате действия нескольких обобщённых сил, равна половине суммы произведений обобщённых сил на соответствующие обобщённые перемещения, получающиеся от совместного действия всех обобщённых сил:

Видео:Построение эпюр в балке ( Q и M ). СопроматСкачать

Вычисление потенциальной энергии

Потенциальная энергия деформации U равна работе внешних сил W (см. — здесь).

Рассмотрим отдельные виды деформаций.

Растяжение -сжатие

Кручение

Изгиб

При вычислении потенциальной энергии будем предполагать, что деформации не только материала, но и всей конструкции, следуя закону Гука, пропорциональны нагрузкам, т. е. линейно с ними связаны и растут постепенно вместе с ними. Множитель ½ появился здесь как следствие того, что нагружение является статическим и деформации упруги – работа внешних сил измеряется площадью заштрихованного треугольника.

Из полученных выражений следует, что потенциальная энергия деформации равна половине произведения силы или пары сил на перемещение по ее направлению в том сечении, где эта сила приложена.

Таким образом, в общем случае можно записать:

, где U — потенциальная энергия деформации, W — работа внешних сил, P₀ — любой силовой фактор (растягивающая сила, крутящий момент и тому подобное) называется обобщённой силой ; δ₀ — соответствующая этой силе деформация (удлинение, угол закручивания, угол поворота и тому подобное) называется обобщённым перемещением (или — обобщенная координата).

Под обобщённой силой Р₀ следует понимать не одну силу, а уравновешенную систему сил (включая сюда и реактивные усилия), которая производит деформацию.

Видео:Перемещения при изгибе. Часть 3.2. Методы, основанные на уравнивании постоянныхСкачать

Энергетические методы определения деформаций

Для определения перемещений при изгибе (прогибов и углов поворота сечений балок) существуют различные методы (способы). Это интеграл (формула) Мора, метод начальных параметров, метод (правило) Верещагина, формула Симпсона. Кроме них существует более общий метод, пригодный для определения деформаций любых упругих конструкций. Он основан на применении закона сохранения энергии.

Представим, что к стержню подвешен груз. При статическом растяжении упругого стержня происходит превращение потенциальной энергии из одного вида в другой; часть потенциальной энергии действующего на стержень груза (уменьшение) за счёт перемещения нижнего конца стержня полностью переходит в потенциальную энергию деформации стержня (увеличение).

Действительно, если мы будем нагружать стержень путем постепенного подвешивания к его нижнему концу очень малых грузов dP, то при добавлении каждого такого груза подвешенная уже часть нагрузки опустится, и ее потенциальная энергия уменьшится, а потенциальная энергия деформации стержня соответственно увеличится. Это явление имеет место при любом виде деформации всякой упругой конструкции при статической нагрузке; такую конструкцию можно рассматривать как своеобразную машину, преобразующую один вид потенциальной энергии в другой.

Статической называется такая нагрузка, которая возрастает постепенно и таким образом, что ускорениями элементов конструкции можно пренебречь; передача давлений (сил) от одной части конструкции на другую не меняет характера движения этих частей, т. е. их скорость остается постоянной и ускорение отсутствует. При этих условиях деформация конструкции не будет сопровождаться изменением кинетической энергии системы, и будет иметь место лишь преобразование потенциальной энергии из одного вида в другой.

При этом мы пренебрегаем магнитными, электрическими и тепловыми явлениями, сопровождающими упругие статические деформации тела лишь в очень слабой мере. Так как характер движения всех элементов конструкции с течением времени не меняется, то в каждый момент времени будет иметь место равновесие как для каждой части конструкции в целом под действием внешних сил и реакций, так и для каждого элемента этой части под действием внешних сил и напряжений, приложенных к этому элементу.

Деформации конструкции, напряжения в ее частях и реакции, передающиеся от одной части на другую, успевают следовать за ростом нагрузки.Таким образом, можно сказать, что полное преобразование одного вида потенциальной энергии в другой имеет место, если деформация происходит без нарушения равновесия системы.

Мерой энергии, превратившейся в другой вид, является величина работы, произведенной силами, действующими на конструкцию.

Обозначим величину накопленной потенциальной энергии деформации через U, а уменьшение потенциальной энергии внешних нагрузок U_F. Тогда величина U_F измеряется положительной работой этих нагрузок W_F, с другой стороны, накоплению потенциальной энергии деформации U соответствует отрицательная работа внутренних, междучастичных сил W, так как перемещения точек тела при деформации происходят в обратном по отношению к внутренним силам направлении.

Закон сохранения энергии при деформациях упругих систем принимает вид:

Заменяя в этой формуле величины U_F и U численно равными им значениями работ W_F и —W, получаем иную формулировку этого закона:

W_F = —W или W_F + W = 0

Эта формулировка закона сохранения энергии совпадает с так называемым «началом» возможных перемещений в применении к упругим системам. Последнее равенство выражает, что при перемещениях без нарушения равновесия сумма работ всех сил, приложенных к точкам тела, равна нулю. Таким образом, начало возможных перемещений в применении к упругим системам является следствием закона сохранения энергии. А потенциальная энергия деформации U численно равна работе внешних сил W_F, проделанной ими этой деформации:

Видео:Лабораторная работа "Определение перемещений в балке при изгибе"Скачать

Формула Симпсона для определения перемещений

Для определения перемещения по формуле Симпсона необходимо:

1. Построить грузовую эпюру моментов (эпюру моментов от действия всех внешних нагрузок).
2. Построить единичную эпюру моментов. Для этого в сечении, где нужно определить линейное перемещение (прогиб) приложить единичную силу, а для определения углового перемещения — единичный момент, и от данного единичного фактора построить эпюру изгибающих моментов.
3. Перемножить эпюры (грузовую и единичную) по формуле, которая называется формулой Симпсона:

где l_i – длина участка;

EI_i – жесткость балки на участке;

– значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.

Видео:Сопротивление материалов. Лекция: дифференциальное уравнение изогнутой оси балкиСкачать

Правило Верещагина (способ перемножения эпюр)

Во многих случаях интегрирования по Мору можно избежать и применить способ«перемножения» эпюр. Одним из таких способов является способ Симпсона, но также можно определить перемещения по способу (правилу) Верещагина. Этот способ А.К. Верещагин предложил в 1924 году, будучи студентом.

Рассмотрим последовательность действий по правилу Верещагина. Начальный этап такой же, как по формуле Мора и способу Симпсона, т.е. вначале строится грузовая эпюра от действующих нагрузок (действительное состояние), затем рассматриваем балку во вспомогательном состоянии. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила, равная единице , а если требуется найти угол поворота, то приложить следует сосредоточенную пару сил, момент, равный единице. Строится эпюра единичных моментов или эпюра от единичной нагрузки. Далее перемещение вычисляется по формуле:

, где в числителе — произведение площади грузовой эпюры на ординату единичной (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры, а в знаменателе — жесткость сечения.

Этот способ становится понятным,если доказать, что результат перемножения двух эпюр ,одна и которых произвольна ,а другая линейна, равен произведению площади грузовой эпюры на ординату единичной, взятой под центром тяжести грузовой эпюры.

Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной(EI=Const),
2. Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

Пусть грузовая эпюра произвольна, а единичная линейна (так как единичной нагрузкой бывает обычно либо сосредоточенная сила, либо пара сил, то единичная эпюра М 0 оказывается ограниченной прямыми линиями). Пусть грузовая эпюра М(z) имеет криволинейное очертание, а эпюра М 0 – прямолинейное (см. рисунок). Произведение можно рассматривать как элемент площади эпюры М, заштрихованной на рисунке.

Так как ордината М 0 равна то произведение , а весь интеграл , где

— статический момент площади эпюры М(z) относительно оси ординат

Но! Статический момент площади ,как известно, это произведение самой площади на координату центра тяжести. Тогда

, где — это

ордината в единичной эпюре, расположенной под центром тяжести грузовой эпюры. Окончательно, перемещение равно:

Таким образом, результат перемножения двух эпюр равен произведению площади грузовой эпюры на ординату другой (обязательно прямолинейной), взятой под центром тяжести грузовой эпюры.

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс», а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Видео:Определение перемещений при изгибе балкиСкачать

Определение перемещений

Виды перемещений. Дифференциальное уравнение упругой линии балки

При плоском изгибе балки её упругая линия, лежащая в плоскости действия внешних сил, искривляется, точки этой линии получают некоторые перемещения.

Произвольно выбранная точка С перемещается как в направлении, перпендикулярном АВ, так и вдоль этой линии на величину . Наибольший практический интерес представляет перемещение , которое называется прогибом балки. Угол между направлениями 1-1 и 2-2 называется углом поворота сечения балки. Таким образом , перемещения бывают линейные и угловые.

Наряду с расчётом балки на прочность необходимо производить и расчёт на жёсткость, то есть определять прогибы и углы поворота балки. Существует несколько способов решения задачи о деформациях балок. Рассмотрим аналитический способ. Установим зависимость координаты – уравнение упругой линии.

Из рисунка видно ,что Но! В упругой стадии работы материала углы поворота настолько малы ,что можно считать угол равным его тангенсу. Вспомнив геометрический смысл производной, можно принять угол поворота равным первой производной прогиба по абсциссе сечения.

Правила знаков для перемещений, знаки перемещений

Угол считается положительным, если сечение поворачивается против хода часовой стрелки и наоборот. Прогиб считают положительным согласно принятому направлению осей координат. Если ось координат направлена вверх, то положительным будет прогиб вверх, а отрицательным — вниз.

Для нахождения зависимости y=f(z) используем известное соотношение между кривизной оси с изгибающим моментом и жесткостью сечения балки

При постоянных моменте, кривизне и жесткости балка изгибается по окружности.

Из математики известно, что кривизна кривой может быть выражена так:

Пренебрегая получим приближённое дифференциальное уравнение изогнутой оси балки:

При приближённом дифференциальном уравнении изогнутой оси балки пользуются принципом малости перемещений, а если перемещения очень большие, то используют точное дифференциальное уравнение. В технике допускаемая величина прогиба , где — длина пролёта балки. Уравнение представляет собой линейное дифференциальное уравнение второго порядка с разделяющимися переменными и может быть проинтегрировано в общем виде:

где v- линейное перемещение (прогиб), θ – угловое перемещение, С₁ и С₂ – постоянные интегрирования.

С₁– угол поворота в начале координат, умноженной на величину ЕI;

С₂ – прогиб балки в начале координат, умноженный на EI.

Значения этих постоянных определяют из граничных условий ,т.е. условий опирания балки и условий на границах смежных участков. Вот эти условия:

— у свободно лежащей балки прогибы на обеих опорах равны нулю. При симметричном нагружении у такой балки угол поворота в середине пролета также равен нулю;

— у консольной балки в заделке и прогиб и угол поворота равны нулю;

— на границе смежных участков балки прогиб и угол поворота одинаковы как для левого, так и для правого участка.

Определение перемещений по методу начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

где у₀ и φ₀ – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:

Порядок определения перемещений по универсальным формулам:

1. Определить все опорные реакции.
2. Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
3. Ось у направить вверх, ось z — вдоль балки.
4. Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
5. Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.

б) Каждая внешняя сила (Мi, Fi, qi) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

Видео:Построение эпюр при изгибе. Часть 1. Консольная балкаСкачать

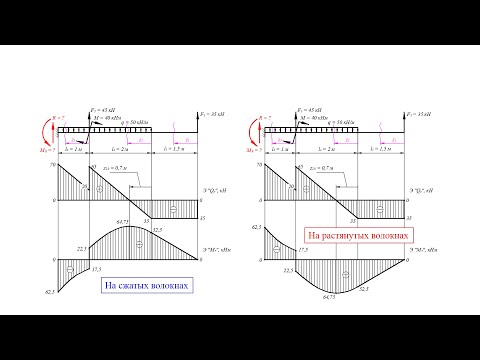
Определение перемещений. Метод О. Мора в сочетании со способом (формулой) Симпсона

Для определения любого перемещения (линейного или углового) в методе Мора балка рассматривается в двух состояниях: действительном и вспомогательном. Вспомогательное состояние получается следующим образом: сначала всю заданную нагрузку нужно удалить, затем приложить «единичный силовой фактор» в том месте, где требуется определить перемещение, и по направлению этого искомого перемещения. Причем, когда определяем линейное перемещение (прогиб балки), то в качестве «единичного силового фактора» принимается сосредоточенная сила , а если требуется найти угол поворота, то приложить следует сосредоточенную пару .

Далее в одном и том же произвольном сечении обоих состояний (то есть и действительного, и вспомогательного) составляются аналитические выражения изгибающего момента, которые подставляются в формулу, называемую «интегралом Мора»:

где: знак Σ распространяется на все участки балки,

а EI – изгибная жесткость на участке.

Во многих случаях интегрирования по Мору можно избежать и применить способ «перемножения» эпюр. Одним из таких способов является способ Симпсона, по которому значение интеграла Мора на участке длиной ℓ вычисляется по следующей формуле:

Здесь обозначено: a, b и с – соответственно крайние и средняя ординаты эпюры изгибающих моментов действительного состояния М,

— крайние и средняя ординаты эпюры изгибающих моментов, но только вспомогательного состояния .

Правило знаков: если обе «перемножаемые» ординаты в двух эпюрах расположены по одну сторону от оси эпюры (то есть они одного знака), то перед их произведением мы должны поставить знак «плюс: а если они по разные стороны от оси эпюры, то перед произведением ставим знак «минус».

Следует иметь в виду, что способы «перемножения» эпюр (кроме способа Симпсона известен еще способ Верещагина) применимы только при наличии двух условий:

1. Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
2. Одна из двух эпюр моментов на этом участке должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.

При наличии нескольких участков на балке, удовлетворяющих указанным двум условиям, формула для определения перемещений принимает вид:

Если результат вычисления получается положительным, то, следовательно, направление искомого перемещения совпадает с направлением «единичного силового фактора» ( ), а если результат отрицательный, значит искомое перемещение происходит в направлении, противоположном этому фактору.

Формула Симпсона, записанная через моменты, выглядит следующим образом: перемещения (прогиб или угол поворота) равны

где li – длина участка;

EIi – жесткость балки на участке;

M_F – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

При перемножении эпюр будет полезным для определения ординат эпюр изгибающих моментов:

Задача

Определить угол поворота сечения на левой опоре φ_А

1) Находим опорные реакции действительного состояния .

2) Строим эпюру моментов действительного состояния М.

3) Выбираем вспомогательное состояние для определения угла поворота φ_А.

4) Находим опорные реакции вспомогательного состояния

«Реагируем» на знак «минус».

5) Строим эпюру моментов вспомогательного состояния:

6) «Перемножаем» эпюры

Поскольку одна из них (а именно ) линейна на всем пролете и не имеет перелома, а эпюра М тоже без перелома, то в формуле Симпсона будет всего один участок, и тогда

Знак «плюс» говорит о том, что сечение А поворачивается в сторону «единичного момента»

Видео:Метод начальных параметров ( МНП ). СопроматСкачать

Определение перемещений. Метод начальных параметров

Метод начальных параметров (или по универсальным формулам прогибов и углов поворота сечений)

где у₀ и φ₀ – начальные параметры, то есть прогиб и угол поворота в начале координат, которые определяются из условий закрепления балки:

Порядок определения перемещений по универсальным формулам:

1. Определить все опорные реакции.
2. Поместить начало координат обязательно в крайнее сечение балки (левое или правое).
3. Ось у направить вверх, ось z — вдоль балки.
4. Найти начальные параметры из условий закрепления балки (возможные случаи показаны выше).
5. Зная начальные параметры у₀ и φ₀, по универсальным формулам определить интересующие нас перемещения.

При использовании универсальных формул необходимо выполнять следующие требования:

а) В универсальные формулы включать только те внешние силы, которые действуют между началом координат (т.0) и сечением, в котором определяются перемещения. Следует помнить, что опорные реакции – тоже внешние силы.

б) Каждая внешняя сила (М_i, F_i, q_i) вводится со знаком изгибающего момента, который эта сила вызывает в сечении, где определяется перемещение.

Задача

Найти прогиб конца консоли.

1. Задаемся направлениями опорной реакции А и реактивного момента в заделке М_А и составляем уравнения статики:

откуда А = q·2 + F = 10·2 + 20 = 40кН,

откуда

1. Помещаем начало координат в заделку (т.0).
2. Ось у направляем вверх, ось z – вдоль балки (вправо).
3. Формулируем условия закрепления балки при выбранном расположении начала координат:

Реализуем эти условия с помощью универсальных формул:

1. Учитывая найденные значения у₀ и φ₀, с помощью формулы прогибов найдём прогиб конца консоли:

при z = 4м

Знак «плюс» результата говорит о том, что прогиб конца консоли происходит в положительном направлении оси у, то есть вверх.

Для получения численного значения прогиба результат следует разделить на изгибную жёсткость балки ЕI, то есть