Условие
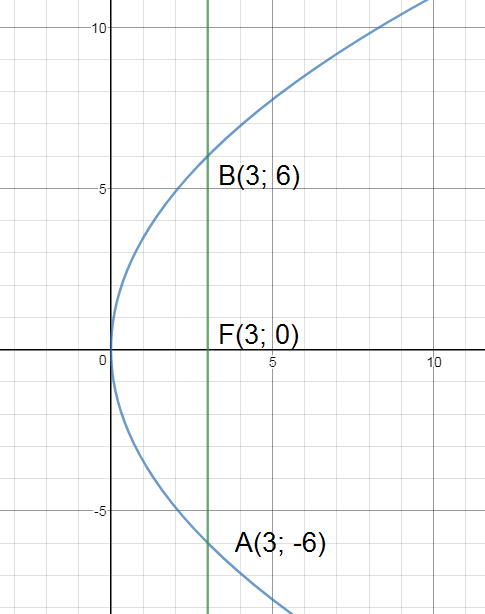
4.3.114) Через фокус параболы у^2 = 12х проведена хорда, перпендикулярная к ее оси. Найти длину хорды.
Решение
Каноническое уравнение параболы имеет вид:
y^2=2px ( p > 0)
F(p/2;0) — фокус параболы.
у^2 = 12х
2p=12
p=6
F(3;0)
х=3 — прямая, проходящая через фокус перпендикулярно оси параболы.
Находим точки пересечения прямой x=3 и параболы y^2=12x
y^2=12*3
y^2=36
y_(1)=-6 или y_(2)=6
Прямая x=3 пересекает параболу в точках
A(3:-6) и В (3;6)
d=AB=|y_(2) — y_(1)| = |6 — ( — 6)| =12
О т в е т. 12. 
Видео:Как определить уравнение параболы по графику?Скачать
Уравнение параболы и длина хорды
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
Глава 22. Диаметры линий второго порядка
В курсе аналитической геометрии доказывается, что середины параллельных хорд линии второго порядка лежат на одной прямой. Эта прямая называется диаметром линии второго порядка. Диаметр, делящий пополам какую-нибудь хорду (а значит, и все параллельные ей), называется сопряженным этой хорде (и всем хордам, который ей параллельны). Все диаметры эллипса и гиперболы проходят через центр. Если эллипс задан уравнением
(1)
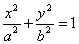
то его диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
.
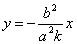
Если гипербола задана уравнением
, (2)
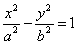
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
.
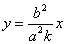
Все диаметры параболы параллельны ее оси. Если парабола задана уравнением
,
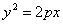
то ее диаметр, сопряженный хордам с угловым коэффициентом k , определяется уравнением
.
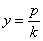
Если один из двух диаметров эллипса или гиперболы делит пополам хорды, параллельные другому, то второй диаметр делит пополам хорды, параллельные первому. Такие два диаметра называются взаимно сопряженными.
Если k и k ’ — угловые коэффициенты двух взаимно сопряженных диаметров эллипса (1), то
(3)
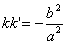
Если k и k ’ — угловые коэффициенты дух взаимно сопряженных диаметров гиперболы (2), то
(4).
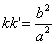
Соотношения (3) и (4) называются условиями сопряженности диаметров соответственно для эллипса и для гиперболы.
Диаметр линии второго порядка, перпендикулярный к сопряженным хордам, называется главным.
Видео:Окружнось. Зависимость длины хорды, от длины дуги.Скачать
Высшая математика (стр. 27 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
или 
.
Пример 38. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ох и отсекающей от прямой 
хорду длиной 
.
Решение. Прямая проходит через начало координат 
, так как является биссектрисой I и II координатных углов. Искомая парабола симметрична относительно оси Ох, поэтому уравнение параболы может иметь вид 
или 
. Рассмотрим каждый из этих случаев. Если , то вторая точка пересечения прямой с параболой , 
, значит и 
, то есть точка 
. Длина хорды определяется как расстояние между двумя точками и : 
, 
, 
, тогда 
, а значит искомое уравнение параболы
.
Рассмотрим второй случай, когда уравнение параболы имеет вид . Найдем точки пересечения параболы и данной прямой.
, 
, 
, 
, 
. Получили две точки и 
.
Далее, рассуждая аналогично первому случаю, получаем: 
, , . Тогда искомое уравнение параболы 
.
Таким образом, условиям задачи удовлетворяют два уравнения параболы: и .
Можно сделать вывод, что общее уравнение кривой второго порядка (2.41) может быть уравнением параболы, если коффициенты 
, 
или 
, 
, то есть одна из переменных должна быть в первой степени.
Но не всякое уравнение вида (2.41) определяет кривую второго порядка. Например, не существует точек плоскости, удовлетворяющих уравнению 
.
Задачи для самостоятельного решения.
1. Дана точка 
. Составить уравнение окружности, диаметром которой служит отрезок ОА.
2. Составить уравнение окружностьи, проходящей через точки 
и 
, если ее центр лежит на прямой 
.
3. Эллипс, симметричный относительно осей координат, проходит через точки 
и 
. Составить уравнение эллипса и найти расстояния точки М от фокусов.
4. Эллипс, симметричный относительно осей координат, проходит через точки 
и 
. Составить уравнение эллипса и найти эксцентриситет. Построить эллипс.
5. Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллпса 
.
6. Составить уравнение гиперболы, если ее эксцентриситет равен 2 и фокусы совпадают с фокусами эллипса 
. Построить гиперболу.
7. Составить уравнение параболы, симметричной относительно оси Ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной к оси Ох, равна 16, а расстояние этой хорды от вершины равно 6.
8. Парабола 
отсекает от прямой, проходящей через начало координат, хорду, равную 
. Составить уравнение этой прямой.
Ответы. 1. 
. 2. 
.
3. 
; 
. 4. 
. 5. 
. 6. 
. 7. 
. 8. 
.
Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка».
Даны вершины треугольника 
, 
, 
. Найти 1) уравнение стороны АВ; 2)угол при вершине А; 3) уравнение и длину высоты CD; 4) точку пересечения медианы треугольника. Сделать чертеж.
1.1. 
, 
, 
.
1.2. 
, 
, 
.
1.3. 
, 
, 
.
1.4. 
, 
, 
.
1.5. 
, 
, 
.
1.6. 
, 
, 
.
1.7. 
, 
, 
.
1.8. 
, 
, 
.
2.1. Составить каноническое уравнение эллипса, у которого малая полуось равна 4, а расстояние между фокусами равно 10.
2.2. Определить координаты центра и радиус окружности 
.
2.3. Составит уравнение гиперболы, проходящейц через точки 
и 
.
2.4. На параболе 
найти точку, расстояние которой до директрисы параболы равно 4.
2.5.Составить каноническое уравнение эллипса, зная, что большая полуось равна 6, а эксентриситет 
.
2.6. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10, а между вершинами 8.
2.7. Составить уравнение параболы, симметричной относительно оси Оу, проходящей через точку 
, вершина которой лежит в начале координат.
2.8. Определить координаты центра и радиус окружности 
.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Красс для экономических специальностей. – М.: ИНФРА-М, 1998.
2. Солодовников в экономике. Ч.1,2. – М.: Финансы и статистика, 1999.
3. Беклемишев аналитической геометрии и линейной алгебры. – М.: Наука, 1984.
4. Ефимов курс аналитической геометрии. – М.: Наука, 1975.
5. Крамер математика для экономистов. – М.: ЮНИТИ, 1998.
6. , , Кожевникова математика в упражнениях и задачах. Ч.1. – М.: Высшая школа, 1980.
7. , Никольский линейной алгебры и аналитической геометрии. – М.: Наука, 1980.
8. Лопатников -математический словарь. – М.:Наука, 1993.
9. Шипачев высшей математики. – М.: Высшая школа, 1994.
10. Шипачев задач по высшей математике. – М.: Высшая школа, 1994.
1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 4
1.1. Определители 4
1.1.1. Определители второго порядка 4
1.1.2. Опренделители третьего порядка 4
1.1.3. Свойства определителей 7
1.1.4. Определители четвертого порядка
Методы их вычисления. 11
1.2.1. Основные понятия 15
1.2.2. Действия над матрицами 18
1.2.3. Обратная матрица 23
1.2.4. Ранг матрицы 28
1.3. Системы линейных уравнений 33
1.3.1. Основные понятия 33
1.3.2. Теорема Кронекера – Копелли 34
1.3.3. Матричный метод решения систем 41
1.3.4. Решение систем линейных уравнений по формулам Крамера 43
1.3.5. Решение систем методом Гаусса 45
1.3.6. Однородные системы уравнений 49
Индивидуальное домашнее задание по теме «Элементы линейной алгебры» 55
2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ 57
2.1. Векторы. Основные понятия 57
2.2. Линейные операции над векторами 58
2.3. Проекция вектора на ось 61
2.4. Координаты вектора 64
2.5. Деление отрезка в данном отношении 68
2.6. Скалярное произведение векторов и его свойства 70
2.7. Векторное произведените векторов и его свойства 74
2.8. Смешанное произведение векторов и его свойства 78
Контрольная работа по теме «Векторная алгебра» 81
2.9. Прямая на плоскости 83
2.10. Кривые второго порядка 94
Контрольная работа по теме «Элементы аналитической геометрии и кривые II порядка» 108
📸 Видео
Как найти длину хорды по радиусу и центральному углу. Геометрия 8-9 классСкачать
Как легко составить уравнение параболы из графикаСкачать
Окружность, диаметр, хорда геометрия 7 классСкачать
Длина параболы и спирали Архимеда: что у них общего?Скачать
Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать
Расчет сегмента окружности по хорде и длине цилиндрической поверхности (трансцендентное уравнение)Скачать
Окружность. Длина хорды. Теорема синусов.Скачать
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Задача на нахождение длины хорды окружностиСкачать
ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать
Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать
ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
§24 Каноническое уравнение параболыСкачать
9 класс, 6 урок, Уравнение окружностиСкачать
