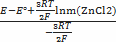Уравнение нернста для концентрационного элемента составленного из двух амальгамных электродов (7 видео)

Химические цепи без переноса (приведите пример). Зависимость ЭДС

Химических цепей без переноса от активности потенциалопределяющих ионов в

Растворе. Вывод и анализ уравнения Нернста.

Электрохимические цепи по наличию или отсутствию в цепи границы двух различных растворов (а значит и диффузионного потенциала) разделяют на цепи с переносом или без переноса соответственно.

В химических цепях источником электрической энергии является химическая реакция, протекающая в электрохимической системе. Химические цепи могут быть с переносом (имеется граница двух растворов или соединение через солевой мостик) и без переноса, где такой границы нет. Химические цепи построены из электродов различных по химической природе.

В гэ без переноса нет диффузионного потенциала, следовательно его не надо устранять. Точность измерения выше.

Примеры цепей без переноса:

Pt, Cl2 | KCl | AgCl(тв), Ag

Концентрационные цепи без переноса, приведите примеры. Для произвольно выбранного концентрационного элемента названного типа запишите химический процесс, протекающий в элементе. Вывод уравнения Нернста для расчёта ЭДС этого элемента.

Различают концентрационные цепи с переносом и без переноса.

Цепи без переноса строят из двух амальгамных электродов с разной концентрацией амальгам, сплавов или двух газовых электродов с разными давлениями газов, погруженных в один и тот же раствор. В этих цепях на электроде с большей концентрацией амальгамы, сплава или с большим давлением газа происходит ионизация атомов металла или газа, активность металла или газа уменьшается. На электроде с меньшей концентрацией будет происходить образование свободных атомов металла или молекул газа, их активность возрастает. Таким образом, в результате работы концентрационной цепи происходит выравнивание активностей компонентов на обоих электродах. Как и в химических цепях, электрод, на котором идет восстановление (присоединение электронов), будет положительным, где окисление – отрицательным.

Pt | Cl2 | KCl | Cl2 | Pt

71) Классификация гальванических элементов. Примеры концентрационных цепей. Уравнение Нернста для концентрационного элемента, составленного из двух амальгамных электродов. Определение полярности электродов.

Электрические цепи обычно классифицируют по двум признакам:

1) по источнику электрической энергии они делятся на химические и концентрационные;

2) по наличию или отсутствию в цепи границы двух различных растворов (а значит и диффузионного потенциала) на цепи с переносом или без переноса соответственно.

В концентрационных цепях оба электрода идентичны как по физической природе, так и по химической природе участников окислительно–восстановительных процессов. Они отличаются только концентрациями компонентов. Знаки электродов определяются по реакциям на электродах, приводящим к выравниванию концентраций (активностей) веществ электродов.

Различают концентрационные цепи с переносом и без переноса.

Концентрационная цепь с переносом:

Ag | AgNO3 :: AgNO3 | Ag

Zn (Hg) | ZnSO4 | Zn(Hg)

В процессе выравнивания концентраций на правом электроде будет происходить образование (восстановление) цинка по реакции:

Zn(2+)+2ē = Zn (Hg) (a2)

Следовательно он положительный.

На левом – растворение (окисление) цинка:

Zn (Hg) (a1) = Zn(2+)+2ē

Следовательно он отрицательный.

Zn (Hg) (a1) = Zn (Hg) (a2)

E= -(RT/zF)*ln(a2/a1) > 0

72) . Концентрационные гальванические элементы, составленные из двух электродов первого рода, электрохимическая цепь с переносом. Уравнение Нернста для расчета ЭДС элемента. Дайте обоснование приведенного уравнения.

Концентрационная цепь с переносом:

(-)Ag | AgNO3 :: AgNO3 | Ag (+)

В ходе работы этого элемента активности должны выравниваться, т.е. а1 возрастать, а а2 убывать

E = (RT/zF)*ln(a2/a1) > 0

73) Концентрационные гальванические элементы. Приведите пример концентрационного гальванического элемента, составленного из двух электродов второго рода. Как определить полярность электродов данного элемента? Запишите уравнение Нернста для представленного элемента и дайте необходимые пояснения.

выводила сама, не уверена

(-) Ag | AgBr | Br(-) :: Br (-) | AgBr | Ag (+)

Ag+ (а1) Br (-)= AgBr + ē

AgBr + ē= Ag +(а2) Br(-)

Зависимость ЭДС гальванического элемента от температуры. Определение изменения термодинамических функций окислительно-восстановительных реакций потенциометрическим методом. Проиллюстрируйте процедуру расчета на произвольном примере

Предложите гальванический элемент, с помощью которого возможно определить средний ионный коэффициент активности соли AB (дан конкретный сильный электролит) в водном растворе. Получите выражение для расчета коэффициента активности

Средний коэффициент активности электролита и, следовательно, среднюю активность электролита можно определить методом измерения электродвижущих сил гальванических элементов без переноса. Для этого используют элемент, составленный из электродов, один из которых обратим по отношению к катионам, а другой – по отношению к анионам соединения. Электроды опускают в один и тот же раствор электролита.

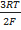
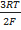
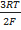
E=E°- lna_±(_ZnCl₂₎ ; a_±(_ZnCl₂₎ =γ ₍_Zn 2+ ₎ *m ₍_ZnCl₂₎ ; E=E°- lnγ₍_Zn 2+ ₎ — lnm₍_ZnCl₂₎

lnγ _(ZnCl2) =

Предложите гальванический элемент, с помощью которого можно определить рН исследуемого раствора. Запишите уравнение Нернста для каждого из электродов электрохической цепи. Получите уравнение для расчета рН раствора.

При измерении рН р-ра в качестве индикаторного электрода обычно используют стеклянный, электродом сравнения мб хлорсеребряный или каломельный электрод.

Если в качестве электрода сравнения применить хлорсеребряный, то электрохимическая цепь будет иметь вид:

E_{ст =} E _ст°- lna₍_H₊₎ и рН =

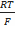
Пример,

Составьте гальванический элемент, по измеренной ЭДС которого возможно определить парциальное давление азота в азот-водородной газовой смеси, находящейся под давлением Р. Запишите уравнение Нернста для используемого гальванического элемента, назовите все входящие в него величины.

Содержание

Концентрационные элементы
Решение задач с использованием уравнения Нернста (Nernst)
Решение задач по химии с использованием уравнениея Нернста
🌟 Видео

Видео:Составление схемы и вычисление ЭДС гальванического концентрационного элемента | Уравнение НернстаСкачать

Концентрационные элементы

Формула Нернста позволяет подойти к другой важнейшей электрохимической проблеме — концентрационным элементам, которыми насыщены наша природа и живые организмы.

На границе контакта растворов, имеющих различную концентрацию ионов, возникает ЭДС. Поскольку электродный потенциал металла зависит от концентрации иона в растворе, можно составить гальванический элемент из одинаковых металлических электродов, погруженных в растворы с различной концентрацией ионов этого металла. Соберем гальванический элемент из двух электродов из одного металла, погруженных в растворы с различной концентрацией их ионов С, и С₂ моль/л, причем С₂> C_v Лучше вместо каких-либо металлов взять два платиновых электрода.

Составим два уравнения Нернста для двух электродов:

Электрод с меньшей концентрацией ионов имеет более высокую способность посылать ионы в раствор, и его электроны будут переходить на другой электрод с более высокой концентрацией ионов. Поэтому при С₂ > С, имеем

В данном случае при С, = 0,01 моль/л, С₂ = 0,1 моль/л получим

Таким образом, десятикратное различие в концентрациях ионов двух электродов создает ЭДС всего в 0,03 В.

Работа концентрационного элемента состоит в том, что металл, погруженный в более разбавленный раствор, отдавая свои ионы раствору, растворяется, а на электроде, опущенном в более концентрированный раствор, эти ионы разряжаются и осаждается металл. Выравнивание концентраций ионов в двух растворах, т.е. действие концентрационного элемента, будет происходить до тех пор, пока концентрации не станут равными.

С точки зрения термодинамических представлений электрический ток вырабатывается концентрационным элементом за счет стремления системы перейти в состояние с равномерным распределением ионов во всех ее частях, т.е. в состояние с максимальной энтропией.

Концентрационные элементы широко используют в химических исследованиях, например для определения растворимости, произведения растворимости, константы нестойкости комплексного иона, ионного произведения воды, констант диссоциации кислот и оснований, концентрации ионов водорода, pH растворов и т.п.

Составим гальванический элемент из стандартного водородного электрода с концентрацией (активностью) ионов водорода 1 моль/л и водородного электрода в чистой воде. ЭДС такого элемента равна 0,414 В (при температуре 298,15 К). Рассчитаем концентрацию ионов водорода в воде:

откуда С_н = 1 -10 7 моль/л и pH = 7. Из результатов опыта следует также, что ионное произведение воды К_п = 10 ‘ • 10 7 = 10 м и pH + рОН = 14.

Для установления растворимости электролита определяют ЭДС концентрационного элемента. Предположим, что требуется найти растворимость какой-либо соли, т.е. концентрацию ее в насыщенном растворе. Составим концентрационный элемент из двух электродов, один из которых находится в растворе с известной концентрацией С, а другой — в растворе с искомой концентрацией С_х (рис. 6.7). Потенциалы этих электродов /:, и Е., равны

где Е° — стандартный электродный потенциал катиона соли; п — число участвующих в реакции электронов (заряд катиона).

Рис. 6.7. Концентрационный элемент для измерения растворимости электролита

Определяемая экспериментально электродвижущая сила этого гальванического элемента равна

По значению ЭДС рассчитывают концентрацию С_х катионов в насыщенном растворе и растворимость соли (минерала). При использовании этого метода следует учитывать силу электролита, ионную силу раствора, возможность гидролиза, образования комплексных ионов и другие факторы.

Для точного определения произведения растворимости измеряют ЭДС концентрационного элемента, в котором один электрод представляет собой раствор с известной концентрацией иона, а второй — с концентрацией того же иона над осадком малорастворимого электролита.

В качестве примера рассмотрим определение произведения растворимости бромида серебра. Для этого составим гальванический элемент из двух электродов, одним из которых служит серебряная проволока, погруженная в насыщенный раствор бромида серебра, другим — серебряная проволока в 0,01 М растворе нитрата серебра.

В этой цепи возникает ЭДС, равная 0,245 В. В первом электроде концентрация ионов серебра определяется произведением растворимости бромида серебра:

Так как [Ag + ] = [Вг ], то ПР = [Ag + ] 2 , и тогда [Ag + ] = VTlP. Концентрация ионов серебра С’_Л(,- у второго электрода задается концентрацией нитрата серебра, находящегося в растворе в виде ионов:

откуда IgnP = -12,277 и ПР = 5,28-10 ,3 .

Измерив ЭДС и определив ПР по крайней мере при двух температурах Г, и Т. легко вычислить изменение энтальпии и энтропии при растворении вещества в данном температурном интервале. Для этого достаточно составить и решить систему из двух уравнений с неизвестными ДЯ_р._1СТ и Д5_раст:

Концентрационными элементами насыщены земная кора и живые организмы. Электрические токи концентрационных элементов влияют на магнитное поле земной коры, они участвуют в переносе соединений от одного места влажной земной поверхности к другому. Огромна их роль в поведении океанов и морей, хотя мало изучена.

В живых организмах концентрация ионов калия внутри клетки благодаря выталкиванию ионов натрия почти в 50 раз выше, чем снаружи клетки. Это создает ЭДС 0,6—0,9 В. Внутренняя сторона клеточной мембраны заряжена отрицательно, а наружная — положительно. Биоэлектрические потенциалы обеспечивают нормальную жизнедеятельность организмов.

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

Решение задач с использованием уравнения Нернста (Nernst)

Видео:Уравнение Нернста. Задачи на расчет потенциалов. Продукты в ОВР. Ч.5-2.Скачать

Решение задач по химии с использованием уравнениея Нернста

Задание 246.
Потенциал серебряного электрода в растворе АgNO₃ составил 95% от значения его стандартного электронного потенциала. Чему равна концентрация ионов Аg+ (моль/л). Ответ: 0,20 моль/л.
Решение:
Электродный потенциал металла (Е)зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Используя уравнение Нернста, получим выражение для расчета концентрации ионов Ag + в растворе:

Ответ: 0,20 моль/л.

Задание 247.
Составьте схему, напишите электронные уравнения электродных процессов, и вычислите ЭДС медно-кадмиевого гальванического элемента, в котором [Сd 2+ ] = 0,8 моль/л, а [Сu 2+ ] = 0,01 моль/л. Ответ: 0,68 В.
Решение:
Схема данного гальванического элемента:

Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки — границу раздела двух жидких фаз — пористую перегородку (или соединительную трубку, заполненную раствором электролита). Кадмий имеет меньший потенциал (—0,403 В) и является анодом, на котором протекает окислительный процесс:

Cd 0 — 2 = Cd 2+ (1)

Медь, потенциал которой +0,34 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Cu 2+ + 2 = Cu 0 (2)

Уравнение окислительно-восстановительной реакции, характеризующее работу данного гальванического элемента, можно получить, сложив электронные уравнения анодного (1) и катодного (2) процессов:

Cd 0 + Cu 2+ = Cd 2+ + Cu 0

Электродный потенциал металла (Е) зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Определим электродные потенциалы кадмия и меди при заданных концентрациях:

Для определения ЭДС гальванического элемента из потенциала катода следует вычесть потенциал анода. Так как концентрация ионов в растворе 1 молы/л, то ЭДС элемента равна разности стандартных потенциалов двух его электродов:

Ответ: 0,68 В.

Задание 248.
Составьте схемы двух гальванических элементов, в одном из которых медь была бы катодом, а в другом — анодом. Напишите для каждого из этих элементов электронные уравнения реакций, протекающих на катоде и на аноде.
Решение:
а) Схема гальванического элемента, в котором медь является катодом:

Вертикальная линейка обозначает поверхность раздела между металлом и раствором, а две линейки — границу раздела двух жидких фаз — пористую перегородку (или соединительную трубку, заполненную раствором электролита). Цинк имеет меньший потенциал (-0,763 В) и является анодом, на котором протекает окислительный процесс:

Zn 0 — 2 = Zn 2+ (1)

Медь, потенциал которой +0,34 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Cu 2+ + 2 = Сu 0 (2)

Zn 0 + Cu 2+ = Zn 2+ + Cu 0

б) Схема гальванического элемента, в котором медь является анодом:

Медь имеет меньший потенциал (+0,34 В) и является анодом, на котором протекает окислительный процесс:

Cu 0 — 2 = Cu 2+ (1)

Платина, потенциал которой +1,19 В, катод, т.е. электрод, на котором протекает восстановительный процесс:

Pt 2+ + 2 = Pt 0 (2)

Сu 0 + Pt 2+ = Cu 2+ + Pt 0

Задание 249.
При какой концентрации ионов Сu 2+ (моль/л) значение потенциала медного электрода становится равным стандартному потенциалу водородного электрода? Ответ: 2,98 . 10 -12 моль/л..
Решение:
Определим концентрацию ионов Cu 2+ , при которой потенциал медного электрода равен 0,00 В, получим:

Ответ: 2,98 . 10 -12 моль/л.

Задание 250.
Какой гальванический элемент называют концентрационным? Составьте схему, напишите электронные уравнения электродных процессов и вычислите ЭДС гальванического элемента, состоящего из серебряных электродов, опущенных: первый в 0,01 н., а второй в 0,1 н. растворы AgNO₃. Ответ: 0,059 В.
Решение:
Гальванический элемент, работа которого основана на различных концентрациях ионов металла у катода и у анода, называется концентрационным. Обычно катод и анод сделаны из одного и того же металла, опущенных в растворы своей соли разной концентрации. Электродный потенциал металла (Е) зависит от концентрации его ионов в растворе. Эта зависимость выражается уравнением Нернста:

Е 0 – стандартный электродный потенциал металла; n – число электронов, принимающих участие в процессе; с – концентрация ионов металла в растворе его соли (при точных вычислениях – активность). Определим электродные потенциалы серебряных электродов при разных концентрациях ионов серебра Ag+, получим: