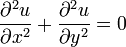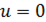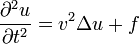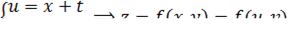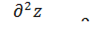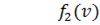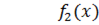Уравнение лапласа в декартовых координатах и полярных координатах (2 видео)

ОПЕРАТОР ЛАПЛАСА В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ. ПОНЯТИЕ О ВОЛНОВОМ УРАВНЕНИИ. ПАДАЮЩАЯ И ОТРАЖЕННАЯ ВОЛНА.

План лекции

1. Оператор Лапласа в полярной системе координат.

2. Понятие о волновом уравнении.

3. Падающая и отраженная волна.

o Оператор Лапласа в полярной системе координат

Оператор Лапласа — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом . Функции он ставит в соответствие функцию

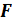
Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции: , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом , то есть в виде скалярного произведения оператора набла на себя. Оператор Лапласа унитарен.

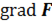
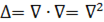
Уравнение Лапласа — дифференциальное уравнение в частных производных. В трёхмерном пространстве уравнение Лапласа записывается так:

Уравнение рассматривают также в двумерном и одномерном пространстве. В двумерном пространстве уравнение Лапласа записывается:

В полярных координатах 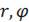уравнение Лапласа имеет вид:

o Понятие о волновом уравнении

Волновое уравнение — линейное гиперболическое дифференциальное уравнение в частных производных, задающее малые поперечные колебания тонкой мембраны или струны, а также другие колебательные процессы в сплошных средах (акустика, преимущественно линейная: звук в газах, жидкостях и твёрдых телах) и электромагнетизме (электродинамике). Находит применение и в других областях теоретической физики, например при описании гравитационных волн. Является одним из основных уравнений математической физики.

В многомерном случае однородное волновое уравнение записывается в виде:

где — оператор Лапласа, — неизвестная функция, — время, — пространственная переменная, — фазовая скорость.

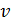
Вывод для трёхмерного случая: в одномерном случае уравнение называется также уравнением колебания струны или уравнением продольных колебаний стержня и записывается в виде:

Разность называется оператором Даламбера и обозначается как . Таким образом, с использованием оператора Даламбера однородное волновое уравнение записывается как:

Допустимо также рассматривать неоднородное волновое уравнение:

где 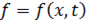— некая заданная функция внешней силы.

Стационарным вариантом волнового уравнения является уравнение Лапласа (уравнение Пуассона в неоднородном случае).

Задача нахождения нормальных колебаний системы, описываемой волновым уравнением, приводит к задаче на собственные значения для уравнения Лапласа, то есть к нахождению решений уравнения Гельмгольца, получающегося подстановкой

или .

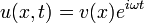
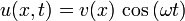
o Падающая и отраженная волна

Длинная линия — регулярная линия электропередачи, длина которой превышает длину волны колебаний, распространяющихся в ней, а расстояние между проводниками, из которых она состоит, значительно меньше этой длины волны.

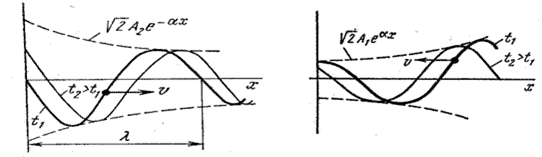
Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным к линии генератором электромагнитных колебаний, и называется падающей. Другая волна называется отражённой, и возникает из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

*Слева – падающая волна, справа – отраженная

Физически эффект уменьшения амплитуд падающей и отраженной волн по мере их продвижения по линии объясняется наличием потерь в линии.

На рисунке слева изображены графики распределения падающей волны напряжения вдоль линии (в функции ) для двух смежных моментов времени: и . Падающая волна распространяется слева направо. При построении принято .

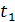
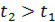
На рисунке справа представлены графики распределения отраженной волны напряжения для двух смежных моментов времени: 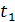и .

Отраженная волна распространяется справа налево.

Отношение напряжения отраженной волны в конце линии к напряжению падающей волны в конце линии называют коэффициентом отражения по напряжению и обозначают .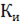

Фазовой скоростью называют скорость, с которой нужно перемещаться вдоль линии, чтобы наблюдать одну и ту же фазу колебания, или иначе: фазовая скорость — это скорость перемещения по линии неизменного фазового состояния.

Пример падающей волны:

0 1 2

Снимок волны при , при . Если , , если , то

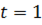
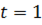
1 2

0 1 2 3

Скорость волны – .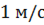

Контрольные вопросы:

1. Что такое оператор Лапласа? Уравнение Лапласа? Как записывается уравнение Лапласа в полярных координатах?

2. Что называется волновым уравнением? Как записывается волновое уравнение?

3. Что такое оператор Даламбера?

4. Что называется длинной линией, отраженной волной, падающей волной?

5. Что такое коэффициент отражения по напряжению?

Содержание

1. Уравнение Лапласа в сферических координатах¶
Криволинейные координаты¶
Локальный базис и коэффициенты Ламе¶
Элемент длины¶
Метрический тензор¶
Лапласиан в криволинейных координатах¶
Сферические координаты¶
📺 Видео

Видео:Оператор Лапласа в полярных координатахСкачать

1. Уравнение Лапласа в сферических координатах¶

Нас интересует решение дифференциального уравнения в частных производных второго порядка вида $$Delta f = frac + frac + frac = 0,$$ которое называется уравнением Лапласа. Здесь $x, y, z$ — прямоугольные координаты, $f = f(x, y, z)$ — функция, которая удовлетворяет уравнению, то есть является его решением, $Delta = nabla^2 = frac + frac + frac$ — оператор Лапласа («лапласиан»).

Функции, имеющие непрерывные производные первого и второго порядков и удволетворяющие уравнению Лапласа называются гармоническими.

В геодезических приложениях уравнение Лапласа решают либо в сферических, либо в эллипсоидальных координатах (но не геодезических!). Прежде, чем приступать к конкретному решению, сначала надо выразить лапласиан в этих координатах. Представляется удобным однако выработать некоторые общий подход к этой проблеме и ввести криволинейные координаты.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Криволинейные координаты¶

Положение произвольной точки в трёхмерном пространстве задаётся в прямоугольных координатах $x, y, z$ её радиус-вектором $$mathbf = x mathbf + y mathbf + z mathbf,$$ где $(mathbf, mathbf, mathbf)$ — единичные базисные векторы, направленные вдоль осей декартовой системы координат.

Пусть теперь заданы некие криволинейные координаты $q_1, q_2, q_3$ (пример: сферические ($r,vartheta, lambda$), геодезические ($H, B, L$)). Они однозначно связаны с прямоугольными координатами $x, y, z$ гладкими функциям $varphi_1, varphi_2, varphi_3$:

$$ left <beginx = varphi_1left(q_1,;q_2,;q_3right),\ y = varphi_2left(q_1,;q_2,;q_3right), \ z = varphi_3left(q_1,;q_2,;q_3right).endright.$$

Системы координат образуются пересекающимися координатными поверхностями, которые можно построить, зафиксировав одну из координат $q_i$. На пересечении координатных поверхностей находятся координатные линии, которые можно построить, если зафиксировать две координаты $q_i$. В общем случае координатные поверхности и линии будут кривыми, отсюда и название — криволинейные координаты. Координатые оси направлены по касательным к координатным линиям в точке пересечения координатых поверхностей. В общем случае и в отличие от декартовой системы, координатные оси криволинейной системы координат имеют разное направление в каждой точке пространства.

Пример. Сферическая система координат образована пересечением плоскости меридиана ($lambda = const$), сферы ($r = const$) и бесконечного конуса ($vartheta = const$). Координатными линиями служат: прямая ($lambda=const, vartheta=const$, пересечение плоскости меридиана и бесконечного конуса), дуга большого круга сферы радиуса $r$ ($ r=const, lambda=const$, пересечение сферы и плоскости) и дуга малого круга ($r=const, vartheta=const$, пересечение сферы и бесконечного конуса).

Если в любой точке координатные поверхности и линии попарно ортогональны, то есть касательные к ним попарно перпендикулярны, то система координат называется ортогональной, если под косым углом, то — косоугольной. В геодезии всегда используются только ортогональные системы, поэтому будем рассматривать преимущественно их. Не стоит путать ортогональные и прямоугольные (декартовы) координаты. Последние сами являются ортогональными, а также частным случаем криволинейных.

Локальный базис и коэффициенты Ламе¶

В декартовой системе координат базисные векторы могут быть найдены через частные производные по радиус-вектору: $$ mathbf = dfrac<partial mathbf>,quad mathbf = dfrac<partial mathbf>,quad mathbf = dfrac<partial mathbf>. $$

Составляя аналогичные производные для криволинейной системы $$ mathbf_1 = dfrac<partial mathbf>,quad mathbf_2 = dfrac<partial mathbf>,quad mathbf_3 = dfrac<partial mathbf>, $$ получим локальный базис в текущей точке. В отличие от глобального базиса, например декартовой системы, локальный базис, как и координатные оси, имеет разное направление в каждой точке пространства. В общем случае локальный базис может не быть единичным и не быть ортогональным.

То есть коэффициентами Ламе $h_1, h_2, h_3$, соответствующими данной ортогональной криволинейной системе координат, называются модули частных производных радиуса-вектора $mathbf$ текущей точки по её криволинейным координатам $q_1, q_2, q_3$. В явном и пригодном для вычисления виде это можно записать следующим образом $$ begin h_1 &= left|dfrac<partial mathbf> right| = sqrt< left( dfracright)^2 + left( dfracright)^2 + left( dfracright)^2>,\ h_2 &= left|dfrac<partial mathbf> right| = sqrt< left( dfracright)^2 + left( dfracright)^2 + left( dfracright)^2>,\ h_3 &= left|dfrac<partial mathbf> right| = sqrt< left( dfracright)^2 + left( dfracright)^2 + left( dfracright)^2>. end $$

Через коэффициенты Ламе можно задать криволинейные ортонормированные (то есть ортогональные и единичные) базисные векторы $$ mathbf_1 = dfrac<mathbf_1>, mathbf_2 = dfrac<mathbf_2>, mathbf_3 = dfrac<mathbf_3>. $$

Элемент длины¶

Пусть произвольная точка переместилась на малое расстояние радиус-вектор изменился на величину

$$d mathbf = mathbfdx + mathbf dy + mathbf dz.$$

В ортогональной криволинейной системе координат изменение радиус-вектора можно записать через полный дифференциал следующим образом:

Квадратом линейного элементы (элемента длины, элемента дуги) или метрикой называется скалярный квадрат $ds = dmathbf^2 = dmathbfcdot dmathbf$ полного дифференциала $dmathbf$ радиус-векора $mathbf$ текущей точки

$$ ds^2 = dmathbf^2 = dx^2 + dy^2 + dz^2.$$

Очевидно, что метрика инвариантна к выбору системы координат. В криволинейных координатах получим

$$ ds^2 = h_1^2 dq_1^2 + h_2^2 dq_2 + h_3^2 dq_3^2, $$

где использована формула квадраты суммы трёх слагаемых

$$ (a + b +c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc, $$

а также свойство ортогональности системы координат, для которой справедливо

$$ mathbf_i cdotmathbf_j = begin 0,quad textrm i neq j,\ 1,quad textrm i = j. end $$

Метрический тензор¶

Из выражений для коэффициентов Ламе и квадрата линейного элемента нетрудно сделать обобщение, удобное для автоматизированных вычислений. Если образовать диагональую матрицу $g$, элементами которой будут квадраты коэффициентов Ламе $g_ = h_i h_i$, то найти её можно будет так $$ g = J^T J, $$ где $J$ — матрица Якоби, а $J^T$ — транспонированная ей.

Матрица $g_$ это на самом деле не матрица, а метрический тензор, записанный в матричной форме. Тензоры это отдельный класс объектов в линейной алгебре, которые являются обобщением и скаляров, и векторов. Почему он метрический? Потому что хотя запись тензора будет меняться при изменении системы координат, некоторые свойства тензора при этом останутся неизменными.

Например, элемент длины теперь выражается следующим образом

где применено правило суммирования Эйнштейна, когда повторяющиеся индексы суммируются (то есть опускается знак суммы: $sum_^3 c_i x^i = c_i x^i$), для чего индексы у $q_i$ записаны сверху $q^i$.

Лапласиан в криволинейных координатах¶

Применение метрического тензора также позволяет записать лапласиан компактно $$ Delta f = frac1<sqrt>frac left( sqrt g^ fracright), $$ где $g^$ это тензор, обратный метрическому, $det g$ — определитель тензора $g$.

Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

Сферические координаты¶

В геодезии уравнение Лапласа чаще всего решают в сферических координатах $r, vartheta, lambda$, которые связаны с прямоугольными координатами $x, y, z$ следующими соотношениями: $$ %left <beginbegin x &= r sinvarthetacoslambda,\ y &= r sinvarthetasinlambda,\ z &= r cosvartheta. end %endright. $$ Здесь $r$ — радиус-вектор, $vartheta = 90^circ — varphi$ — полярное расстояние, являющееся дополнением геоцентрической долготы $varphi$ до $90^circ$, $lambda$ — геоцентрическая долгота.

Обратный переход осуществляется так: $$ begin r &= sqrt,\ vartheta &= arctan<frac<sqrt>>,\ lambda &= arctan<frac>. end $$

Для вывода уравнения Лапласа в сферических координатах можно было бы пойти самым прямым и незамысловатым путём, то есть найти вторые производные $frac, frac, frac$, пользуясь указанными выше связями прямоугольных и сферических координат. Это чрезвычайно громоздкий и тернистый путь. Можете попробовать на досуге. Мы же пойдём чуть более простой дорогой, не зря же вводили криволинейные координаты.