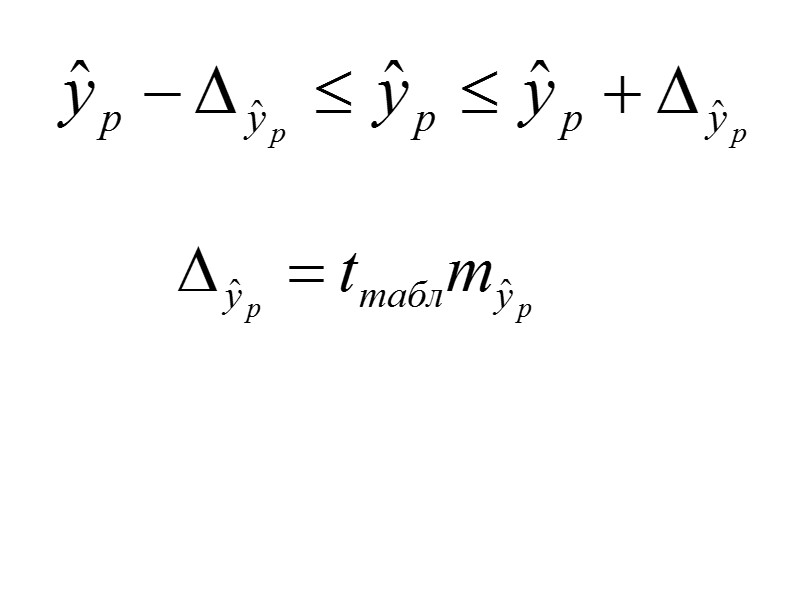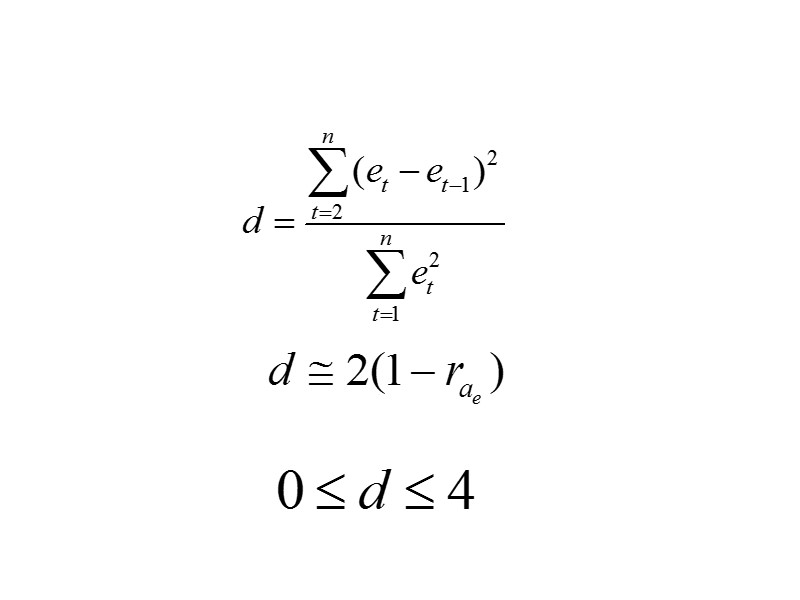Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_0.jpg» alt=»>Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость» /> Оценка значимости уравнения множественной регрессии (F-критерий): Если Fфакт > Fтабл, то признается статистическая значимость и надежность уравнения. Если Fфакт » />
частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_2.jpg» alt=»>частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и» /> частный F-критерий Во множественной регрессии оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Это связано с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный F-критерий, т.е. Fxi.
Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_3.jpg» alt=»>Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в» /> Частный F-критерий Частные критерии Fx1 оценивает статистическую значимость включения фактора x1 в уравнение множественной регрессии после другого фактора , т.е. Fx1 оценивает целесообразность включения в уравнение x1 после включения в него, например, фактора x2.
Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_4.jpg» alt=»>Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно» /> Методика построения Fxj Частный F-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что для регрессии с двумя факторами оцениваем значимость влияния Х1 как дополнительно включенного в модель фактора. Используем следующую формулу:
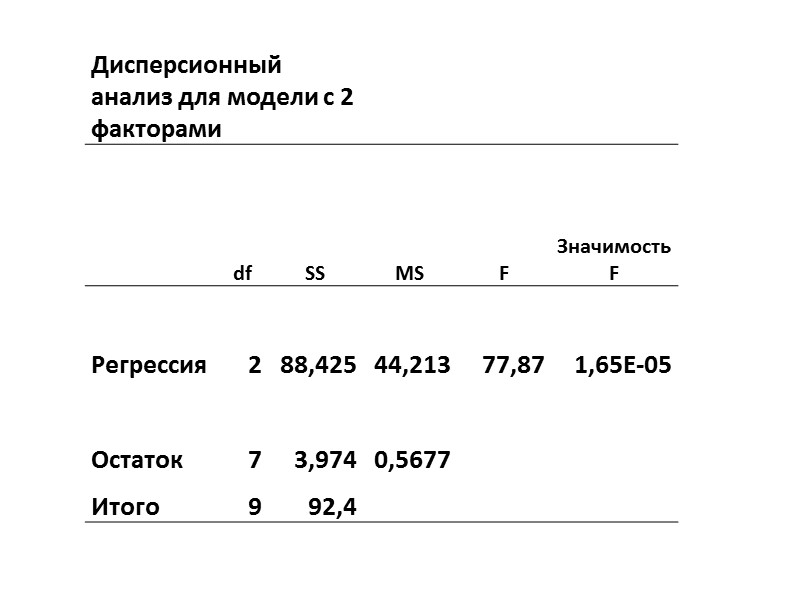
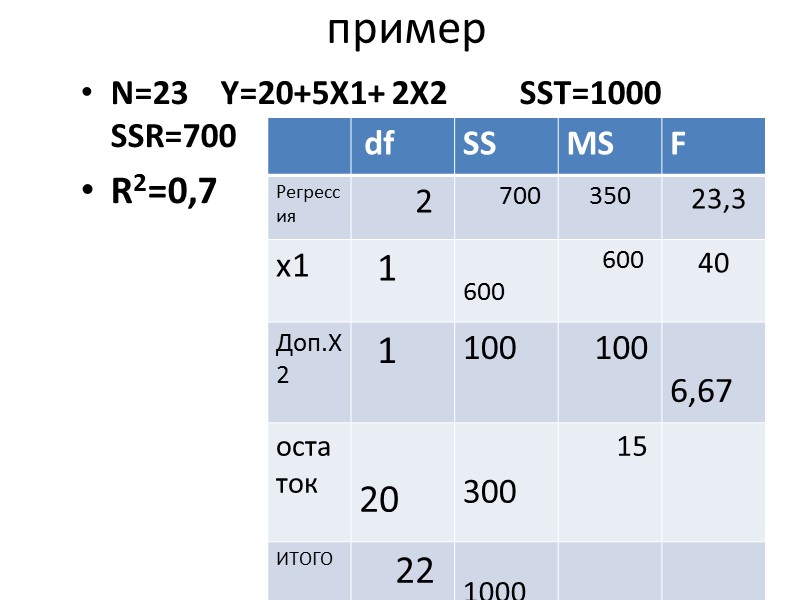
пример N=23 Y=20+5X1+ 2X2 » src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_6.jpg» alt=»>пример N=23 Y=20+5X1+ 2X2 » /> пример N=23 Y=20+5X1+ 2X2 SST=1000 SSR=700 R2=0,7 r2yx1=0,6
Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_7.jpg» alt=»>Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35″ /> Fx2 Fx2 =(0,7-0,6) x 20/0,3 =6,67 F(a=0,05; 1 и 20)=4,35
Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_8.jpg» alt=»>Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том» /> Зная величину Fxi можно определить и t – критерий для коэффициента регрессии при i-том факторе.
связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_9.jpg» alt=»>связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе» /> связь частного Fкритерия Частный F-критерий связан с частной корреляцией. Частный F-критерий в числителе формулы содержит прирост факторной дисперсии, т.е сокращение остаточной дисперсии, которая учитывается в частной корреляции. Поэтому отсев факторов при построении модели множественной регрессии возможен при использовании как частной корреляции, так и частного F-критерия, а также t-критерия Стьюдента и стандартизованных коэффициентов регрессии (β).
Прогноз по множественной регрессии» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_10.jpg» alt=»>Прогноз по множественной регрессии» /> Прогноз по множественной регрессии
Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_12.jpg» alt=»>Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов» /> Модели на основе рядов динамики Модели изолированного динамического ряда. Модели системы взаимосвязанных рядов динамики. Модели автрегрессии. Модели с распределенным лагом.
Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_13.jpg» alt=»>Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)» /> Компоненты временного ряда Тенденция (T) Периодические колебания (P) Случайные колебания (E)
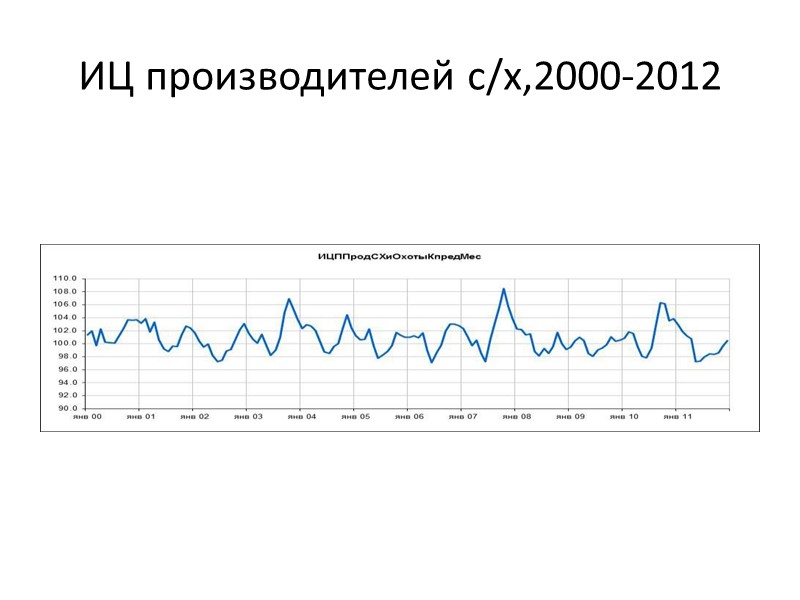
ИЦ производителей с/х,2000-2012″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_14.jpg» alt=»>ИЦ производителей с/х,2000-2012″ /> ИЦ производителей с/х,2000-2012
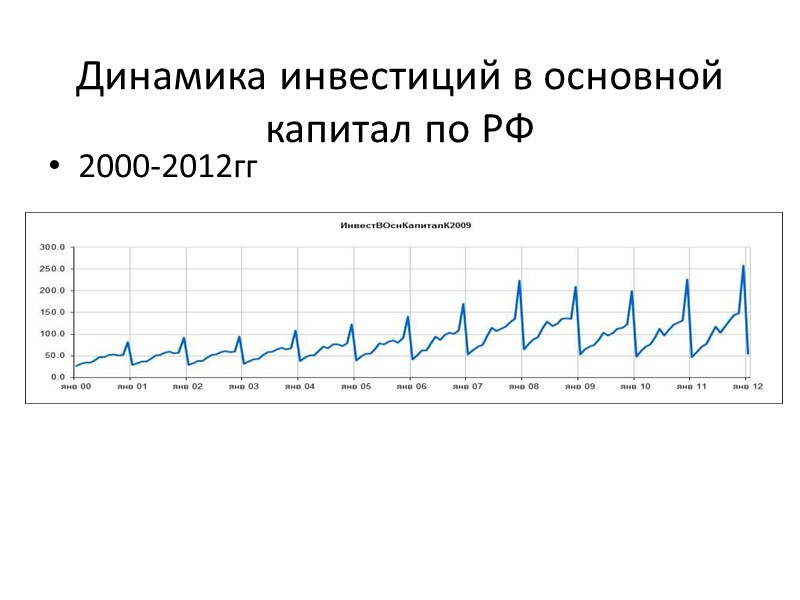
Динамика инвестиций в основной капитал по РФ 2000-2012гг» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_15.jpg» alt=»>Динамика инвестиций в основной капитал по РФ 2000-2012гг» /> Динамика инвестиций в основной капитал по РФ 2000-2012гг
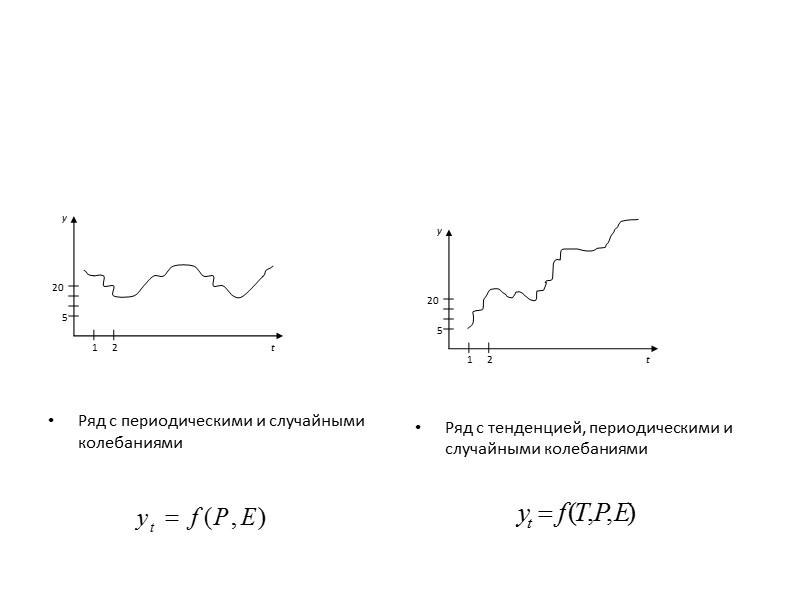
Ряд с периодическими и случайными колебаниями Ряд» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_16.jpg» alt=»>Ряд с периодическими и случайными колебаниями Ряд» /> Ряд с периодическими и случайными колебаниями Ряд с тенденцией, периодическими и случайными колебаниями
Аддитивная модель Мультипликативная модель» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_17.jpg» alt=»>Аддитивная модель Мультипликативная модель» /> Аддитивная модель Мультипликативная модель
Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_18.jpg» alt=»>Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда» /> Автокорреляция уровней ряда и ее последствия Корреляционная зависимость между последовательными значениями уровней временного ряда называется автокорреляцией уровней ряда
Уравнения трендов» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_20.jpg» alt=»>Уравнения трендов» /> Уравнения трендов
Линейный тренд» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_21.jpg» alt=»>Линейный тренд» /> Линейный тренд
Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_22.jpg» alt=»>Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12″ /> Линейный тренд :Y=a+bt равным абсолютным приростом (параметр b) индекс потребительских цен за 12 месяцев = 100,5 + 2t, где t = 1, 2,…, 12 у1=102,5; у12=124,5
Парабола 2-го порядка» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_23.jpg» alt=»>Парабола 2-го порядка» /> Парабола 2-го порядка
Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_24.jpg» alt=»>Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)» /> Парабола :Y=a+bt+ct2 постоянное абсолютное ускорение(∆2) параметр «а»−У при t=0 Параметр «с»=0,5(∆2)
численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс.» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_25.jpg» alt=»>численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс.» /> численность детей в возрасте 7 лет за 15 лет Y=323.7+10.8t-1.6t^2, где y – тыс. чел., t = 1, 2,…, 15. ежегодно численность детей сокращалась в среднем с ускорением в 3,2 тыс. чел.
Показательная функция» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_26.jpg» alt=»>Показательная функция» /> Показательная функция
Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_27.jpg» alt=»>Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента» /> Показательная функция Y=ab^t стабильный коэффициент роста (b) Y=13.5*1.5^t Y=13.5e^0.405t−экспонента
Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_28.jpg» alt=»>Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими» /> Степенной тренд При b > 0 она характеризует непрерывный рост уровней с падающими темпами роста, а при b 0 означает, что уровни ряда снижаются во времени» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_29.jpg» alt=»>Равносторонняя гипербола при b > 0 означает, что уровни ряда снижаются во времени» /> Равносторонняя гипербола при b > 0 означает, что уровни ряда снижаются во времени и асимптотически приближаются к параметру а.Так,выручка предприятия за 7 месяев У=400+85/t ,т.е. падающая тенденция, при которой У не может быть меньше 400. Если b » />
Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_31.jpg» alt=»>Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится» /> Оценка параметров уравнения тренда При использовании полиномов разных степеней оценка параметров уравнения тренда производится методом наименьших квадратов (МНК) точно также, как оценки параметров уравнения регрессии на основе пространственных данных. В качестве зависимой переменной -уровни динамического ряда, а в качестве независимой переменной – фактор времени t, который обычно выражается рядом натуральных чисел: 1, 2,…, n.
нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е.» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_32.jpg» alt=»>нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е.» /> нелинейные функции тренла Оценка параметров нелинейных функций проводится МНК после линеаризации, т. е. приведения их к линейному виду.
Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_33.jpg» alt=»>Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования» /> Показательная функция Для оценки параметров показательной кривой Y=ab^t или экспоненты Y=ae^bt путем логарифмирования функции приводятся к линейному виду и применяется МНК к ln Y и t Число зарегистрированных ДТП (на 100000 человек населения) по области за 2005-2013 годы характеризуется данными:105,7; 105,3; 156; 158,1; 160,1; 178; 191,5; 274,6; 287,3.
Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_34.jpg» alt=»>Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598″ /> Для построения системы нормальных уравнений были рассчитаны вспомогательные величины:ln Y получим: ln Y= 4,517598 + 0,123523t, где 4,517598= lna 0,123523=lnb a = e4,5176 = 91,61524 b = e0,12352 = 1,131476 Соответственно, имеем экспоненту y=91,615e0,1235t или показательную кривую: Y=91,615*1,1315t. Число ДТПвозрастало в среднем ежегодно на 13,5%.
Использование трендовых моделей для прогнозирования» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_35.jpg» alt=»>Использование трендовых моделей для прогнозирования» /> Использование трендовых моделей для прогнозирования
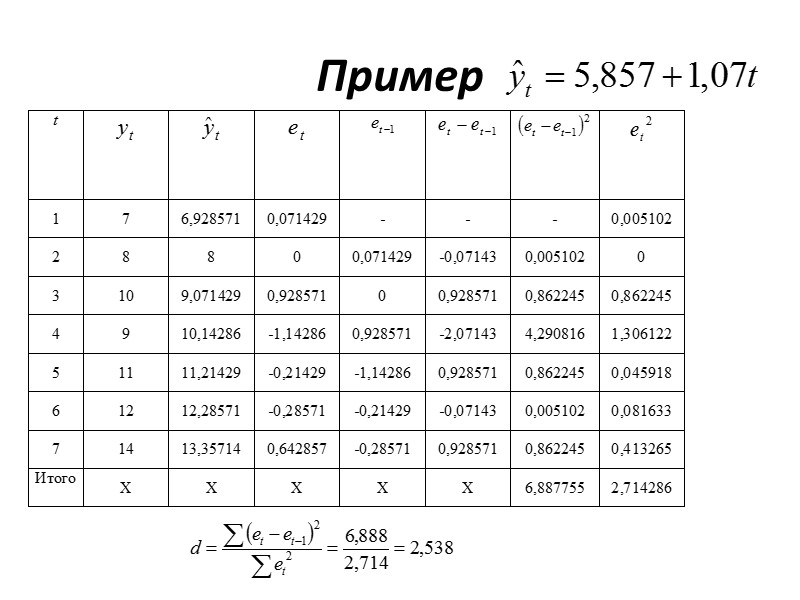
Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7″ src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_36.jpg» alt=»>Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7″ /> Y=13.028+3.0167t t=1.2….9мес. tp =10 Ур=43,19 √ МSост =(14,87/7 )0,5=1,4576-cтандартная ошибка регрессии; Q=(1+(1/9)+(10-5)^2/60)^0,5=1.236 Sp =1,4576* 1.236=1.801- ошибка прогноза a=0.05 ; df=7 ; ta = 2,365 ; ∆р=2,365*1,801=4,26-предельная ошибка прогноза 43,19 ± 4,26 , т .е интервал от 38,9 до 47,4.
Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_37.jpg» alt=»>Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по» /> Оценка адекватности модели тенденции Модель тенденции считается адекватной реальному процессу, если теоретические (найденные по уравнению тренда) уровни ряда достаточно близко подходят к фактическим их значениям. Для оценки адекватности модели проводится анализ остатков . Модели тенденции можно сравнивать по величине остаточной суммы квадратов:S^2=∑(Y – Yteor)^2. Чем меньше эта величина, тем в большей мере уравнение тренда подходит для описания тенденции временного ряда.
Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_38.jpg» alt=»>Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда» /> Предположим, что было рассчитано уравнение линейного тренда и экспоненциального тренда. Для линейного тренда остаточная сумма квадратов составила 3874,62, а для экспоненты 2617,701. Следовательно, экспонента лучше описывает тенденцию ряда. Другим показателем при выборе функции тренда является коэффициент детерминации R2. Чем выше R2, тем соответственно выше вероятность того, что данная модель тенденции описывает исходные данные. В примере R2 для экспоненты составил 0,9202, а для линейного тренда 0,8832, подтверждая еще раз, что экспонента в большей мере подходит для описания тенденции.
Автокорреляция в остатках» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_39.jpg» alt=»>Автокорреляция в остатках» /> Автокорреляция в остатках
автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием,» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_40.jpg» alt=»>автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием,» /> автокорреляция в остатках оценивается также, как и автокорреляция уровней ряда с тем лишь отличием, что в расчетах используются остаточные величины , а не уровни динамического ряда .Пусть коэффициент автокорреляции остатков оказался равным 0,627. Его величина не столь мала, чтобы утверждать об отсутствии автокорреляции остатков. Очевидно уравнение тренда не является наилучшим, ибо нарушена предпосылка МНК об отсутствии автокорреляции остатков.
Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_41.jpg» alt=»>Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего» /> Уравнение тренда хорошо описывает тенденцию, если остатки текущего периода не коррелируют с остатками предыдущего периода. Проверка модели на автокорреляцию остатков обычно проводится с помощью критерия Дарбина-Уотсона.
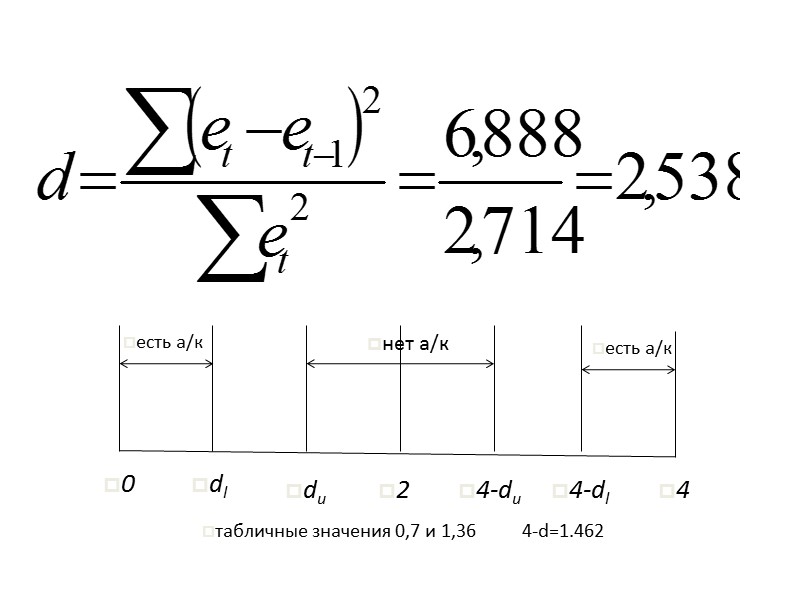
Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий » src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_43.jpg» alt=»>Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий » /> Границы критерия Дарбина-Уотсона При полной положительной автокорреляции остатков (ρ=1 ) критерий d=0, а при полной отрицательной автокорреляции (ρ=−1 ) критерий d=4. Если же автокорреляция в остатках отсутствует, т. е. ρ=0 , то d=2. Иными словами критерий Дарбина-Уотсона изменяется в пределах: 0≤ d ≤ 4.
Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об» src=»https://present5.com/presentacii/20170504/704-prezentaciya_dlya_zaochn..pptx_images/704-prezentaciya_dlya_zaochn..pptx_44.jpg» alt=»>Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об» /> Дарбин и Уотсон разработали пороговые значения показателя d, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции в остатках. При заданном числе наблюдений n (длина динамического ряда) и m параметров при t в уравнении тренда (или m объясняющих переменных в уравнении регрессии) установлены при 5%-ом уровне значимости верхняя (u – upper) и нижняя (ℓ ‑ low) границы критерия.
сравнение с табличными значениями Если d сравнение с табличными значениями Если d сравнение с табличными значениями Если d фактическое значение d › 2 означает отрицательную автокорреляцию, то с пороговыми табличными значениями сравнивается» /> фактическое значение d › 2 означает отрицательную автокорреляцию, то с пороговыми табличными значениями сравнивается величина 4-d. При этом возможны следующие варианты: 1) 4-d ‹ нижней границы: делается вывод о наличии отрицательной автокорреляции в остатках; 2)4-d › верхней границы: отсутствует автокорреляция в остатках; 3) 4-d между нижней и верхней границами: нельзя сделать определенного вывода о наличии или отсутствии автокорреляции в остатках по имеющимся данным
- Метод наименьших квадратов (МНК), линейная аппроксимация
- Постановка задачи на конкретном примере
- Наборы данных
- Графическая иллюстрация метода наименьших квадратов (мнк).
- Сглаживание ряда методом наименьших квадратов
- Суть метода
- Применение надстройки поиск решения
- Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
- Оценка точности
- Вывод формул для нахождения коэффициентов.
- Как реализоавать метод наименьших квадратов в Excel
- Заключение
- Тенденция во временном ряду
- Линейный тренд
- Параметры тренда
- 📽️ Видео
Видео:#1 ЕГЭ. ПАРАМЕТРЫ С НУЛЯ. Что такое параметры? Линейные уравнения с параметрами.Скачать

Метод наименьших квадратов (МНК), линейная аппроксимация
Видео:Прогнозирование в Excel с помощью линий трендаСкачать

Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Наборы данных
Метод наименьших квадратов используется для обработки набора данных и прогнозирования будущих значений. Пусть у нас есть массивы данных X = и Y = , при этом значение Y зависит от X. Придадим этим массивам смысл. К примеру, массив X – это мощность паровой машины парохода, а Y — его ходовая скорость в узлах. Это означает, что при мощности энергетической установки в 10 тысяч лошадиных сил, пароход развивает скорость на уровне 18 морских миль в час, и так далее, так как каждое значение игрека соответствует своему иксу.
Эти данные можно представить в виде точек на декартовой плоскости, например как V1(X1, Y1), V2(X2, Y2) и так далее. Если соединить эти точки, то мы получим некую кривую, которую можем описать соответствующим уравнением y = f(x). Данное уравнение должно быть достаточно простым, но при этом максимально близко описывать полученную зависимость.
Получив кривую, мы можем продлить ее в любую сторону и узнать приблизительное значение игреков для любых иксов или наоборот. Например, аппроксимировав данные нашего примера, мы сможем узнать, какая мощность установки требуется для достижения скорости в 15 узлов. Или какую мы получим скорость, установив на борт установку мощностью в 22 тысячи лошадиных сил. Для того чтобы определить эту волшебную y = f(x), нам и необходим метод наименьших квадратов.
Видео:Excel для полных чайников Урок 16 Линия трендаСкачать
Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 
Дифференциал второго порядка имеет вид:
То есть
Следовательно, матрица квадратичной формы имеет вид
причем значения элементов не зависят от а и b .
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка 

Угловой минор второго порядка
Докажем, что 
Проверим справедливость неравенства для любого значения n, например для n=2.
Получили верное неравенство для любых несовпадающих значений 

Предполагаем, что неравенство верное для n.

Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что 

Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значения а и b соответствуют наименьшему значению функции 
Видео:#10. Уравнение с параметром: выколотая точка!Скачать

Сглаживание ряда методом наименьших квадратов
Задание.
1. Постройте прогноз численности наличного населения города Б на 2010-2011 гг., используя методы: скользящей средней , экспоненциального сглаживания , наименьших квадратов .
2. Постройте график фактического и расчетных показателей.
3. Рассчитайте ошибки полученных прогнозов при использовании каждого метода.
4. Сравните полученные результаты, сделайте вывод.
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t 2 = ∑y•t
| t | y | t 2 | y 2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
Для наших данных система уравнений имеет вид:
9a0 + 45a1 = 524.9
45a0 + 285a1 = 2610.4
Из первого уравнения выражаем а0 и подставим во второе уравнение
Получаем a0 = -0.24, a1 = 59.5
Уравнение тренда:
y = -0.24 t + 59.5
Эмпирические коэффициенты тренда a и b являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Коэффициент тренда b = -0.24 показывает среднее изменение результативного показателя (в единицах измерения у) с изменением периода времени t на единицу его измерения. В данном примере с увеличением t на 1 единицу, y изменится в среднем на -0.24.
Ошибка аппроксимации.
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным.
Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве тренда.
Однофакторный дисперсионный анализ.
Средние значения
Дисперсия
Среднеквадратическое отклонение
Коэффициент эластичности.
Коэффициент эластичности представляет собой показатель силы связи фактора t с результатом у, показывающий, на сколько процентов изменится значение у при изменении значения фактора на 1%.
Коэффициент эластичности меньше 1. Следовательно, при изменении t на 1%, Y изменится менее чем на 1%. Другими словами – влияние t на Y не существенно.
Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где ( y -yt)² = 4.4-1.08 = 3.31
В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 0.3 0.5 0.7 0.9 Полученная величина свидетельствует о том, что изменение временного периода t существенно влияет на y.
Коэффициент детерминации.
т.е. в 75.39% случаев влияет на изменение данных. Другими словами – точность подбора уравнения тренда – высокая.
| t | y | y(t) | (y-ycp) 2 | (y-y(t)) 2 | (t-tp) 2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
m = 1 – количество влияющих факторов в уравнении тренда.
Uy=yn+L±K
где
L – период упреждения; уn+L – точечный прогноз по модели на (n + L)-й момент времени; n – количество наблюдений во временном ряду; Sy – стандартная ошибка прогнозируемого показателя; Tтабл – табличное значение критерия Стьюдента для уровня значимости α и для числа степеней свободы, равного n-2.
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;α/2) = (7;0.025) = 2.365
Точечный прогноз, t = 10: y(10) = -0.24*10 + 59.5 = 57.15
57.15 – 1.08 = 56.07 ; 57.15 + 1.08 = 58.23
Интервальный прогноз:
t = 10: (56.07;58.23)
Точечный прогноз, t = 11: y(11) = -0.24*11 + 59.5 = 56.91
56.91 – 1.14 = 55.77 ; 56.91 + 1.14 = 58.05
Интервальный прогноз:
t = 11: (55.77;58.05)
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | – | – |
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St – значение экспоненциальной средней в момент t;
St-1 – значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt – значение экспоненциального процесса в момент t;
α – вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 – 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 – 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 – 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 – 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 – 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 – 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 – 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 – 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 – 0.1)*56.9 + 0.1*57.54 |
Прогнозирование данных с использованием экспоненциального сглаживания.
Методы прогнозирования под названием “сглаживание” учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 – α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t – 2, t)
Пример . Методом наименьших квадратов найти функции вида y=ax+b , y=ax²+bx+c , аппроксимирующие экспериментальную функцию y=f(x) . В обоих случаях найти суммы квадратов невязок ∑bi². В декартовой системе координат построить экспериментальные точки и графики найденных функций y=ax+b,y=ax^2+bx+c.
Пример №5
Пример №3 . Функция y=y(x) задана таблицей своих значений:
x: -2 -1 0 1 2
y: -0,8 -1,6 -1,3 0,4 3,2
Применяя метод наименьших квадратов, приблизить функцию многочленами 1-ой и 2-ой степеней. Для каждого приближения определить величину среднеквадратичной погрешности. Построить точечный график функции и графики многочленов.
Решение. Функция многочлена 2-ой степени имеет вид y = ax 2 + bx + c .
1. Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК:
a0n + a1∑x + a2∑x 2 = ∑y
a0∑x + a1∑x 2 + a2∑x 3 = ∑yx
a0∑x 2 + a1∑x 3 + a2∑x 4 = ∑yx 2
| x | y | x 2 | y 2 | x y | x 3 | x 4 | x 2 y |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -2 | -0.8 | 4 | 0.64 | 1.6 | -8 | 16 | -3.2 |
| -1 | -1.6 | 1 | 2.56 | 1.6 | -1 | 1 | -1.6 |
| 0 | -1.3 | 0 | 1.69 | 0 | 0 | 0 | 0 |
| 1 | 0.4 | 1 | 0.16 | 0.4 | 1 | 1 | 0.4 |
| 2 | 3.2 | 4 | 10.24 | 6.4 | 8 | 16 | 12.8 |
| 0 | -0.1 | 10 | 15.29 | 10 | 0 | 34 | 8.4 |
Видео:КАК ОПРЕДЕЛЯТЬ ТРЕНД? Глобальный и локальный тренды. ТрейдингСкачать
Суть метода
Данные таблицы можно изобразить на декартовой плоскости в виде точек M1 (x1, y1), … Mn (xn, yn). Теперь решение задачи сведется к подбору аппроксимирующей функции y = f (x), имеющей график, проходящий как можно ближе к точкам M1, M2, ..Mn.
Конечно, можно использовать многочлен высокой степени, но такой вариант не только труднореализуем, но и просто некорректен, так как не будет отражать основную тенденцию, которую и нужно обнаружить. Самым разумным решением является поиск прямой у = ax + b, которая лучше всего приближает экспериментальные данные, a точнее, коэффициентов – a и b.
Видео:Уравнение прямой и его графическая интерпретацияСкачать

Применение надстройки поиск решения
1. Если не включили надстройку «поиск решения», то возвращаемся к пункту Как включить надстройку «поискрешения» и включаем
2. В ячейку А1 введем значение «1». Эта единица будет первым приближением к реальному значению коэффициента (k) нашей функциональной зависимости y=kx.
3. В столбце B у нас расположились значения параметра X, в столбце C — значения параметра Y. В ячейках столбца D вводим формулу: «коэффициент k умножить на значение Х». Например, в ячейке D1 вводим «=A1*B1», в ячейке D2 вводим “=A1*B2” и т.д.
4. Мы считаем, что коэффициент к равен единице и функция f (x)=у=1*х – это первое приближение к нашему решению. Можем рассчитать сумму квадратов разностей между измеренными значениями величины Y и рассчитанными по формуле y=1*х . Можем все это сделать вручную, вбивая в формулу соответствующие ссылки на ячейки: “=(D2-C2)^2+(D3-C3)^2+(D4-C4)^2… и т.д. В конце концов ошибаемся и понимаем, что потеряли кучу времени. В Excel для расчета суммы квадратов разностей есть специальная формула, «СУММКВРАЗН», которая все за нас и сделает. Введем ее в ячейку А2 и зададим исходные данные: диапазон измеренных значений Y (столбец C) и диапазон рассчитанных значений Y (столбец D).
4. Сумму разностей квадратов рассчитали – теперь идем во вкладку «Данные» и выбираем «Поиск решения».
5. В появившемся меню в качестве изменяемой ячейки выбираем ячейку A1 (та, что с коэффициентом k).
6. В качестве целевой выбираем ячейку A2 и задаем условие «установить равной минимальному значению». Помним, что это ячейка, где у нас производится расчёт суммы квадратов разностей расчетного и измеренного значений, и сумма эта должна быть минимальной. Нажимаем «выполнить».
7. Коэффициент k подобран. Теперь можно убедиться, что рассчитанные значения теперь очень близки к измеренным.
Видео:Теория автоматического регулирования. Лекция 5. Модели параметров состоянийСкачать
Аппроксимация функции одной переменной методом наименьших квадратов с дополнительными условиями
Данный калькулятор использует метод наименьших квадратов (МНК) для аппроксимации функции одной переменной, аналогично калькулятору Аппроксимация функции одной переменной . Но, в отличии от указанного калькулятора, данный калькулятор поддерживает аппроксимацию функции с использованием ограничений на ее значения. То есть, можно задать условия равенства аппроксимирующей функции определенным значениям в определенных точках. Формулы аппроксимации будут выведены с учетом этих условий.
Используемый метод (метод множителей Лагранжа) накладывает ограничения на набор аппроксимирующих функций, так что этот калькулятор не поддерживает экспоненциальную аппроксимацию, аппроксимацию степенной функцией и показательную аппроксимацию. Одним словом поддерживается только линейная регрессия. Зато в него были добавлены аппроксимация полиномами 4-ой и 5-ой степени. Формулы и немного теории можно найти под калькулятором.
Если не ввести значения x, калькулятор будет считать, что значение x меняется начиная с 0 с шагом 1.
Видео:✓ Система неравенств с параметром | ЕГЭ-2017. Задание 17. Математика. Профиль | Борис ТрушинСкачать

Оценка точности
При любой аппроксимации особую важность приобретает оценка ее точности. Обозначим через ei разность (отклонение) между функциональными и экспериментальными значениями для точки xi, т. е. ei = yi – f (xi).
Очевидно, что для оценки точности аппроксимации можно использовать сумму отклонений, т. е. при выборе прямой для приближенного представления зависимости X от Y нужно отдавать предпочтение той, у которой наименьшее значение суммы ei во всех рассматриваемых точках. Однако, не все так просто, так как наряду с положительными отклонениями практически будут присутствовать и отрицательные.
Решить вопрос можно, используя модули отклонений или их квадраты. Последний метод получил наиболее широкое распространение. Он используется во многих областях, включая регрессионный анализ (в Excel его реализация осуществляется с помощью двух встроенных функций), и давно доказал свою эффективность.
Видео:№18. Система уравнений с параметром (профильный ЕГЭ)Скачать

Вывод формул для нахождения коэффициентов.
Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 
Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера ) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).
При данных а и b функция 
Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы 



Пришло время вспомнить про исходый пример.
В нашем примере n=5 . Заполняем таблицу для удобства вычисления сумм, которые входят в формулы искомых коэффициентов.
Значения в четвертой строке таблицы получены умножением значений 2-ой строки на значения 3-ей строки для каждого номера i .
Значения в пятой строке таблицы получены возведением в квадрат значений 2-ой строки для каждого номера i .
Значения последнего столбца таблицы – это суммы значений по строкам.
Используем формулы метода наименьших квадратов для нахождения коэффициентов а и b. Подставляем в них соответствующие значения из последнего столбца таблицы:
Следовательно, y = 0.165x+2.184 – искомая аппроксимирующая прямая.
Осталось выяснить какая из линий y = 0.165x+2.184 или 
Видео:Реши любой параметр. Задача 18 Профильный ЕГЭСкачать

Как реализоавать метод наименьших квадратов в Excel
В “Эксель” имеется функция для расчета значения по МНК. Она имеет следующий вид: «ТЕНДЕНЦИЯ» (известн. значения Y; известн. значения X; новые значения X; конст.). Применим формулу расчета МНК в Excel к нашей таблице.
Для этого в ячейку, в которой должен быть отображен результат расчета по методу наименьших квадратов в Excel, введем знак «=» и выберем функцию «ТЕНДЕНЦИЯ». В раскрывшемся окне заполним соответствующие поля, выделяя:
- диапазон известных значений для Y (в данном случае данные для товарооборота);
- диапазон x1, …xn, т. е. величины торговых площадей;
- и известные, и неизвестные значения x, для которого нужно выяснить размер товарооборота (информацию об их расположении на рабочем листе см. далее).
Кроме того, в формуле присутствует логическая переменная «Конст». Если ввести в соответствующее ей поле 1, то это будет означать, что следует осуществить вычисления, считая, что b = 0.
Если нужно узнать прогноз для более чем одного значения x, то после ввода формулы следует нажать не на «Ввод», а нужно набрать на клавиатуре комбинацию «Shift» + «Control»+ «Enter» («Ввод»).
Видео:МНК линейный тренд в MS ExcelСкачать

Заключение
Метод наименьших квадратов — удобный метод для представления данных в виде функции. Благодаря такому представлению вы можете определить любое значение функции, оперируя небольшим набором данных или измерений.
Видео:11. Прямая в пространстве и ее уравненияСкачать

Тенденция во временном ряду
Синонимом тенденции в эконометрике является тренд. Одним из наиболее популярных способов моделирования тенденции временного ряда является нахождение аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называется аналитическим выравниванием временного ряда.
Зависимость показателя от времени может принимать разные формы, поэтому находят различные функции: линейную, гиперболу, экспоненту, степенную функцию, полиномы различных степеней. Временной ряд исследуют аналогично линейной регрессии.
Параметры любого тренда можно определить обычным методом наименьших квадратов, используя в качестве фактора время t = 1, 2,…, n, а в качестве зависимой переменной используют уровни временного ряда. Для нелинейных трендов сначала проводят процедуру линеаризации.
К числу наиболее распространенных способов определения типа тенденции относят качественный анализ изучаемого ряда, построение и анализ графика зависимости уровней ряда от времени, расчет основных показателей динамики. В этих же целях можно часто используют и коэффициенты автокорреляции уровней временного ряда.
Видео:Пример построения схем для уравнения переноса в пространстве неопределенных коэффициентов.Скачать

Линейный тренд
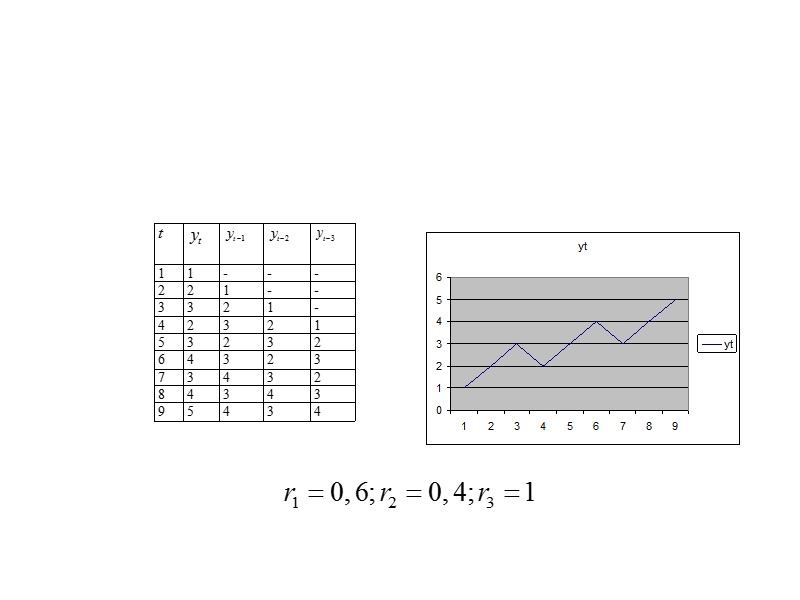
Тип тенденции определяют путем сравнения коэффициентов автокорреляции первого порядка. Если временной ряд имеет линейный тренд, то его соседние уровни yt и yt-1 тесно коррелируют. В таком случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть максимальный. Если временной ряд содержит нелинейную тенденцию, то чем сильнее выделена нелинейная тенденция во временном ряду, тем в большей степени будут различаться значения указанных коэффициентов.
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить перебором основных видов тренда, расчета по каждому уравнению коэффициента корреляции и выбора уравнения тренда с максимальным значением коэффициента.
Параметры тренда
Наиболее простую интерпретацию имеют параметры экспоненциального и линейного трендов.
Параметры линейного тренда интерпретируют так: а — исходный уровень временного ряда в момент времени t = 0; b — средний за период абсолютный прирост уровней рада.
Параметры экспоненциального тренда имеют такую интерпретацию. Параметр а — это исходный уровень временного ряда в момент времени t = 0. Величина exp(b) — это средний в расчете на единицу времени коэффициент роста уровней ряда.
По аналогии с линейной моделью расчетные значения уровней рада по экспоненциальному тренду можно определить путем подстановки в уравнение тренда значений времени t = 1,2,…, n, либо в соответствии с интерпретацией параметров экспоненциального тренда: каждый последующий уровень такого ряда есть произведение предыдущего уровня на соответствующий коэффициент роста
При наличии неявной нелинейной тенденции нужно дополнять описанные выше методы выбора лучшего уравнения тренда качественным анализом динамики изучаемого показателя, для того, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом ряду поворотных точек и изменения темпов прироста, начиная с определенного момента времени под влиянием ряда факторов, и т. д. В том случае если уравнение тренда выбрано неправильно при больших значениях t, результаты прогнозирования динамики временного ряда с использованием исследуемого уравнения будут недостоверными по причине ошибки спецификации.
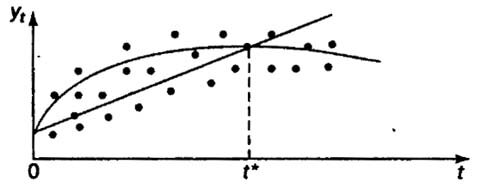
Иллюстрация возможного появления ошибки спецификации приведем на рисунке
Если оптимальной формой тренда является парабола, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция естественно будут по разному описывать тенденцию в уровнях ряда.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
📽️ Видео
#1 КАК РЕШАТЬ ЗАДАЧИ С ПАРАМЕТРОМ. ЛИНЕЙНЫЕ УРАВНЕНИЯ С ПАРАМЕТРОМСкачать

А у тебя идеальный вес?Скачать

Ботаем параметр. Плюс 4 балла на профильном ЕГЭ. 3 эффективных метода решения. Задача 17Скачать

#65. Типичная ЛОВУШКА в задаче с параметром!Скачать

Траектория и уравнения движения точки. Задача 1Скачать

Самый простой метод определения Тренда.Скачать