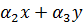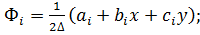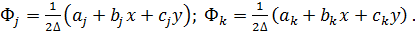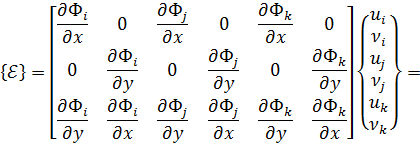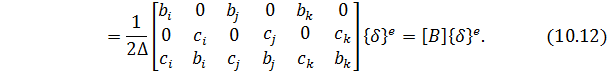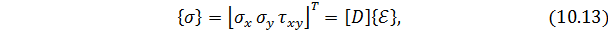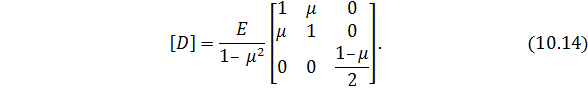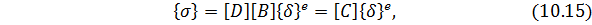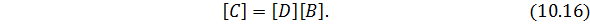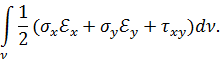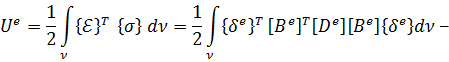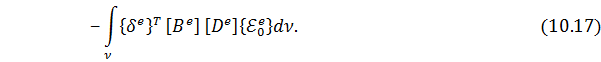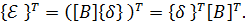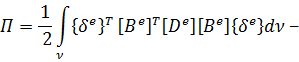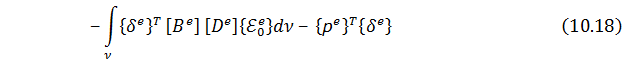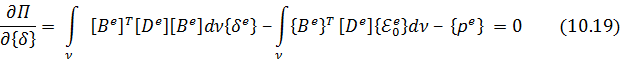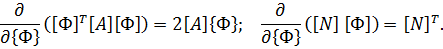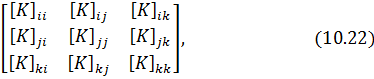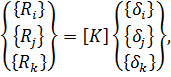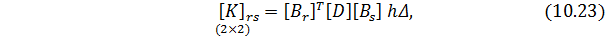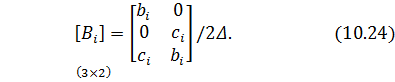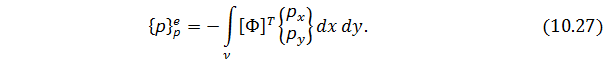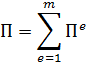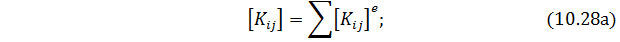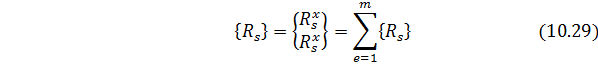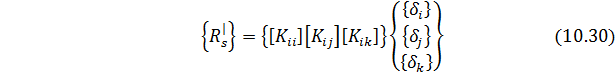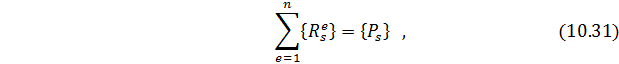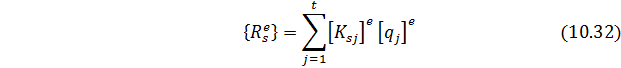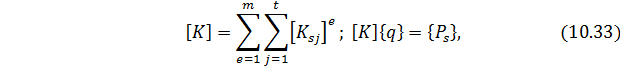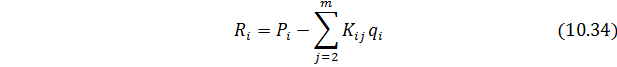10.1. Содержание метода.Метод конечных элементов (МКЭ) представляет
собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т.п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики – метода перемещений. С другой стороны, МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы.
Классический подход к задаче об изучении напряженно-деформированного состояния диска предполагает изучение бесконечно малого его элемента. Получающиеся при этом дифференциальные уравнения в частных производных (равновесия и геометрические) совместно с физическими уравнениями и контурными условиями позволяют определить напряжения, деформации и перемещения в каждой точке диска.
МКЭ предполагает иной подход. Рассматривается элемент конечных размеров (КЭ), за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.
Разделим воображаемыми линиями диск в условиях плоской задачи на некоторое количество элементов конечных размеров, например, треугольной формы и примем за узловые точки их вершины. Очевидно, что если диск находится в равновесии то и его элемент, определенный узлами i, j, k, под воздействием напряжений (усилий) от смежных элементов, также уравновешен. Приложим затем к этому элементу вместо фактических усилий, действующих вдоль его граней, статически эквивалентные узловые силы, т.е. силы, вызывающие внутри элемента действительное напряженно- деформированное состояние.
Поставив в соответствие каждому узловому усилию узловое перемещение, представим сплошной диск набором конечных элементов (КЭ), взаимодействующих между собой в конечном числе узловых точек.
Такой подход позволяет в дальнейшем использовать один из классических методов строительной механики, например метод перемещений (возможно также применение метода сил, либо смешанного). Для этого необходимо установить матрицы жесткости всех КЭ и, из условия равновесия узлов, получить разрешающие уравнения задачи. Найденные узловые перемещения не дают полной характеристики напряженно-деформированного состояния диска. Необходим переход от этих величин к перемещениям, напряжениям и деформациям внутри конечных элементов, т.е. речь идет о решении плоской задачи для каждого КЭ, находящегося под воздействием узловых перемещений. Такой переход в МКЭ осуществляется приближенно, путем задания интерполяционных (координатных) функций (функций формы), что и делает метод приближенным. Функции эти (обычно полиномы) такие, что обеспечивают неразрывность перемещений при переходе от одного элемента к другому. Функции формы однозначно определяют перемещения внутри элемента через узловые перемещения.
Естественно, что при реализации МКЭ возникает необходимость приведения действующих на конструкцию нагрузок к сосредоточенным узловым силам.
Обычно все зависимости, связанные с КЭ , строятся в местной системе координат, с последующим переходом в общую систему для всей области. Это позволяет заранее получить необходимые соотношения для часто применяемых типов КЭ.
Видео:Метод конечных элементов (Часть 1) | Пример реализации для уравнения теплопроводностиСкачать

Алгоритм решения задач по МКЭ содержит следующие этапы:
1. Дискретизация — разбиение заданной области на КЭ; нумерация узлов и КЭ.
2. Аппроксимация перемещений узлов в КЭ.
3. Построение матриц жесткости (МЖ) конечных элементов.
4. Построение глобальной матрицы жесткости общей системы уравнений.
5. Сведение нагрузок и воздействий, приложенных к КЭ, к узловым силам, учет условий закрепления.
6. Решение общей системы уравнений.
7. Определение напряжений и (при необходимости) деформаций в КЭ.
Дискретизация области.Разбиение области на подобласти представляет собой первый шаг на пути к решению задачи, и именно этот шаг не имеет теоретического обоснования. Искусство разбиения области зависит от имеющихся инженерных навыков. Плохое или несовершенное разбиение будет приводить к ошибочным результатам, если даже остальные этапы метода осуществляются с достаточной точностью.
Дискретизация области ( тела ) включает задание числа, размеров и формы подобластей, которые используются для построения дискретной модели реального тела. При этом, с одной стороны, элементы должны быть выбраны достаточно малыми, чтобы получить приемлемые результаты, а с другой стороны, применение достаточно крупных элементов сокращает вычислительную работу.
При решении задач по МКЭ используются элементы различных типов, в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.
Видео:Основы метода конечных элементов. Часть 3. Основные уравнения теории упругости в МКЭСкачать

Разбиение области на элементы.Процесс дискретизации может быть разделен на 2 этапа: разбиение тела на элементы и нумерация элементов и узлов. При разбиении любой двумерной области на элементы сначала тело делится на четырехугольные и треугольные подобласти или зоны, которые затем подразделяются на треугольники. Границы между подобластями должны проходить там, где изменяются геометрия, приложенная нагрузка или свойства элементов.
Наиболее просто можно разбить треугольную подобласть на элементы, если выбрать определенное число узлов вдоль каждой стороны, соединить соответствующие узлы прямыми линиями и точки пересечений этих линий считать узлами.
Четырехугольные зоны обычно разбивают на элементы соединением узлов на противоположных сторонах. Пересечения линий определяют внутренние узловые точки. Внутренние четырехугольники могут расматриваться как элементы или могут быть разбиты на треугольные элементы проведением короткой диагонали в каждом внутреннем четырехугольнике.
Треугольная и четырехугольная зоны могут иметь общую границу. Число узлов на этой границе для обеих зон должно быть одинаковым и относительное положение узлов должно совпадать.
В задачах МДТТ необходимо отметить узлы, которые имеют известные перемещения. Для обозначения неподвижных узлов применяется символ неподвижного шарнира. Если узел может перемещаться только в одном направлении, используется символ подвижного шарнира. Учет узловых условий такого типа осуществляется путем видоизменения общей системы уравнений, решение которой определяет узловые перемещения.
Нумерация узлов. Нумерация узлов влияет на эффективность вычислений, необходимых для получения решения. Использование МКЭ приводит к системе линейных алгебраических уравнений, большее число коэффициентов которой равно нулю. Рассмотрение матрицы коэффициентов системы показывает, что все ненулевые коэффициенты и некоторые нулевые находятся между двумя линиями, параллельными главной диагонали. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю и они не должны сохраняться в памяти ЭВМ. Правильная вычислительная схема использует только те коэффициенты матрицы, которые находятся внутри указанной полосы. Уменьшение ширины полосы приводит к сокращению времени вычислений.
Ширина полосы B вычисляется по формуле
где R – максимальная по элементам величина наибольшей разности между номерами узлов в отдельном элементе; Q — число неизвестных (число степеней свободы в каждом узле). Минимизация величины В связана с минимизацией R, что может быть осуществлено последовательной нумерацией узлов при движении в направлении наименьшего размера тела против часовой стрелки. Правильная нумерация узлов экономит машинную память более чем на 60%, хотя не влияет на вычислительные аспекты задачи.
Построение градиентной матрицы.Для плоского КЭ «e» в форме треугольника с вершинами i, j, k с узловыми координатами соответственно ( 
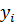
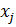
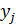
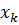
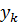
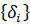
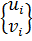
а для трех узлов i, j, k шесть компонент образуют вектор перемещений внутри КЭ «e»:

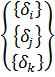
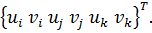
Простейшими интерполяционными функциями являются линейные полиномы
u= 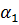
v= 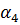
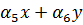
Значения шести постоянных 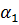
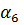
Система уравнений для перемещений u узлов i, j, k:
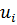
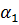
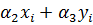
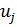
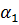
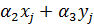
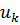
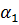
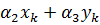
позволяет определить коэффициенты 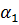
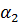
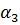
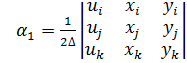
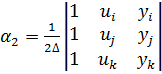
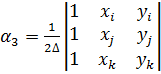
Видео:Основы метода конечных элементов. Часть 1. Идея МКЭ в задачах конструкционного анализаСкачать

где ∆ — площадь треугольника ijk, удвоенное значение которой равно определителю
2∆=det 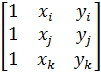
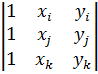
После подстановки 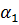
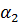
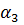
u= 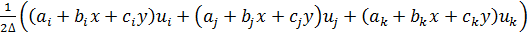
где коэффициенты определяются через координаты узлов КЭ:
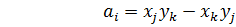
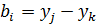
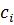
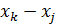
Остальные коэффициенты получаются циклической перестановкой индексов i, j, k.
Аналогично можно представить перемещение v, пользуясь вторым уравнением (10.4):
v= 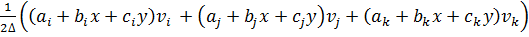
Вектор перемещений внутри КЭ «e»принимает вид
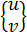
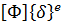

где функции формы 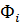
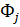
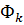

Выбранная функция перемещений автоматически гарантирует неразрывность (совместность) перемещений между смежными КЭ, т.к. вдоль любой стороны треугольника они изменяются линейно; следовательно, из равенства перемещений в узлах следует их равенство по всей границе.
Вектор полной деформации в любой точке КЭ характеризуется тремя составляющими 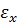
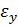
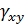
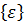
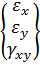
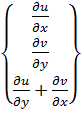
Подставляя (10.10) в (10.11) получим
Матрица 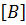
Матрица напряжений.Для упругого изотропного материала физические соотношения т.е. зависимости между напряжениями и деформациями, в данном случае закон Гука, линейны и определяются уравнениями:
где 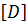
где 𝐸 ‒модуль упругости; 𝜇 ‒ коэффициент Пуассона.
Используя (10.12) и (10.13), напряжения в КЭ 𝑒можно выразить через перемещения его узлов
где матрица 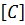
10.2. Матрица жесткости треугольного конечного элемента.МКЭ удобно трактовать как обобщение методов строительной механики стержневых систем на расчет систем континуальных. Тогда он легко распространяется и на комбинированные системы, т.е. системы, содержащие элементы различной мерности. В отличие от стержневых систем, для континуальных систем, в частности, плоской задачи, метод является приближенным.
Матрица жесткости 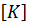
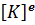
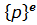
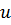
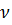
Видео:Метод конечных элементов. Основы 1.1.1 - ВведениеСкачать

где энергия деформации 𝑈 определяется выражением (в соответствии с формулой Клапейрона):
Энергия деформации 𝑈 для КЭ 𝑒, с учетом матричного представления и полученных ранее соотношений
Напомним, что транспонирование произведения двух матриц выполняется по формуле (лк.1 ЧМ ч.1):
Работа 𝐴, совершаемая приложенными силами, может быть разделена на три части:
‒ работа 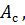
‒работа 
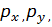
‒работа 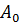
Работу 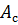
Поверхностные и объемные силы можно также привести к узловым. Тогда
𝐴 = 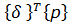

При этом выражение для полной потенциальной энергии для КЭ принимает вид:
Чтобы согласно вариационному принципу Лагранжа минимизировать величину 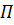
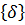
Здесь использованы известные из векторной алгебры формулы дифференцирования произведения матриц по вектору 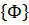
Теперь матрица жесткости элемента 𝑖𝑗𝑘 определяется так:
Отметим единообразие выражений для матриц жесткости стержневых и плоских (10.20) КЭ.
Если толщина 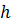
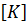
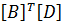
где: Δ ‒ площадь КЭ; 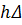
Матрица жесткости является симметричной и имеет блочную структуру:
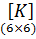
где 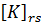
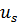

Реактивные усилия в связях, наложенных на узлы 𝑖, 𝑗, 𝑘, вызванные перемещениями 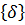
так, например, 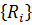
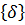
При ОПНС подматрицы имеют второй порядок и определяются следующим образом:
где 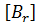
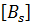
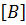
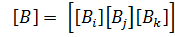
Такая форма записи удобна для компьютерных вычислений.
Видео:Метод конечных элементов. Как получить матрицу жесткости. Начало.Скачать

Узловые силы, связанные с объемными силами X и Y (проекции их интенсивностей на оси x и y), определяются выражениями:
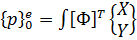

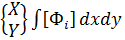
Т.к. функции формы матрицы 
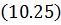
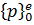
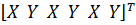
Узловые силы, вызванные поверхностными нагрузками 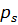
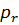
Отметим, что задача о напряженно-деформированном состоянии плоского КЭ решена путем приближенного задания функций формы. Поэтому и метод является приближенным. Увеличить точность решения можно либо путем увеличения числа КЭ, на которое разбивается область Ω, либо путем увеличения числа узловых точек, т.е. числа степеней свободы для каждого из КЭ (последнее путем повышения степени интерполирующего полинома).
10.3. Построение глобальной матрицы жесткости. Поскольку полная потенциальная энергия (функционал) для рассматриваемой области 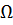
то, минимизируя этот функционал, получим следующую общую систему уравнений:
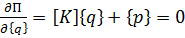
где 
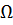
Уравнения (10.28) являются, по сути, уравнениями равновесия. Поскольку координатные функции в методе конечных элементов отличны от нуля только на ограниченной области 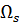
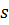
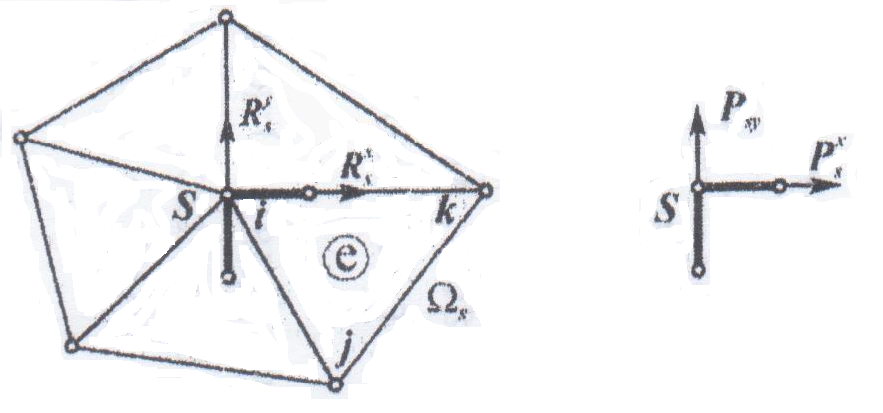
Пусть 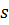
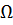
Перемещение любого узла одного из 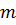
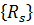
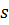
Для показанного на рис. 1 конечного элемента 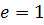
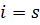
Из условий равновесия узла 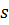
где 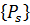
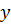
Вектор 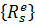
где 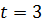
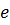
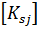
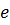
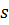

Из подстановки (10.32) в (10.31) следует
где 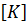
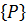
Линейные алгебраические уравнения типа (10.33) составляются для всех узлов расчетной схемы области 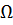

Из матрицы жесткости исключаются те строки и столбцы (а из грузового вектора – элементы), номера которых отвечают узловым связям, наложенный на диск. Обычно, для упрощения индексации, размерность исходной матрицы сохраняют. В случае, если например 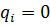
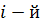
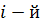
Реакция 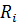
После определения вектора 
🎬 Видео
Метод конечных элементов. КЭ в Лира-СапрСкачать

МКЭ. Метод конечных элементов. Матрица жесткости для ферменного КЭ.Скачать

Основы метода конечных элементов. Часть 2. Функции формы конечного элементаСкачать

Вычислительная гидродинамика (ВГД). Уравнение Рейнольдса и метод конечных объемовСкачать

6-2. Метод сетокСкачать

Метод конечных элементов (FEM) vs метод контрольного объёма (FVM). В чём разница?Скачать

Метод конечных элементов. Основы 1.1.3 - Метод ГалеркинаСкачать
Метод конечных элементов. Основы 1.1.2 - Метод коллокацийСкачать

Олегу Тинькову запрещён вход на Мехмат МГУСкачать

Метод Лапласа решения ДУСкачать

Основы метода конечных элементов. Расчёт элементов фермСкачать

МКЭ. Метод конечных элементов. Применение в инженерной практике.Скачать

Метод конечных элементов. Основы 1.2.2 - Сборка матриц жесткости. Глобальная матрица жесткостиСкачать