Уравнение кривой проходящей через точку 0 3 если угловой коэффициент

Математика | 10 — 11 классы

Найдите уравнение кривой, проходящей через точку М ( — 1 ; 3), если угловой коэффициент касательной в любой точке кривой равен утроенному квадрату абсциссы точки касания.

Угловой коэффициент касательной k — это значение производной в данной точке, по условию k = 3 * x ^ 2, находим уравнение кривой, интегрируя это выражение.

У = интеграл от (3x ^ 2)dx = 3x ^ 3 / 3 + C = x ^ 3 + C.

Кривая проходит через точку ( — 1 ; 3), то подставляем в ее уравнение — 1вместо х, 3 вместо у.

Получаем 3 = ( — 1) ^ 3 + C, откуда С = 4, уравнение искомой кривой у = x ^ 3 + 4.

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 2lnx в его точке с абсциссой х = 2?

Найдите угловой коэффициент касательной, проведенной к графику функции f(x) = 2lnx в его точке с абсциссой х = 2.

Видео:Угловой коэффициент прямойСкачать

Найдите угловой коэффициент касательной , проведенной к графику функции y = 3x — 2cosx в точке с абсциссой Xo = 0?

Найдите угловой коэффициент касательной , проведенной к графику функции y = 3x — 2cosx в точке с абсциссой Xo = 0.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Найдите угол наклона к оси абсцисс касательной, проведённой к кривой f(x) = (x — 3)(x — 2) в точке пересечения этой кривой с осью ординат?

Найдите угол наклона к оси абсцисс касательной, проведённой к кривой f(x) = (x — 3)(x — 2) в точке пересечения этой кривой с осью ординат.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Найти уравнение кривой, проходящей через точку А(5 ; — 1), если угловой коэффициент касательной в любой её точке равен 4х — 8?

Найти уравнение кривой, проходящей через точку А(5 ; — 1), если угловой коэффициент касательной в любой её точке равен 4х — 8.

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Путь, пройденный материальной точкой S = 3t² — 2t + 4?

Путь, пройденный материальной точкой S = 3t² — 2t + 4.

Найти мгновенную скорость точки в конце пятой секунды.

Найти угловой коэффициент касательной, проведённой к кривой у = х³ в точке С( — 2 ; — 8).

Составить уравнение касательной к параболе у = х² — 3х – 1 в точке (3 ; 4).

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Составьте уравнение кривой, проходящей через точку ( — 2 ; 8), если угловой коэффициент касательной в любой тчке касания равен 2x — 4?

Составьте уравнение кривой, проходящей через точку ( — 2 ; 8), если угловой коэффициент касательной в любой тчке касания равен 2x — 4.

Видео:Уравнение прямой линии с угловым коэффициентом проходящей через точкуСкачать

К кривой y = 1 / 2x — x ^ 1 / 2 в некоторой точке проведена касательная с угловым коэффициентом 0?

К кривой y = 1 / 2x — x ^ 1 / 2 в некоторой точке проведена касательная с угловым коэффициентом 0.

25. Найти эту точку касания.

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Найдите угловой коэффициент касательной к графику функции y = 3x — 2cos x в точке с абсциссой x0 = 0?

Найдите угловой коэффициент касательной к графику функции y = 3x — 2cos x в точке с абсциссой x0 = 0.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Записать уравнение касательной к кривой y = x ^ 2 — 7x + 3 в точке с абсциссой x = 1?

Записать уравнение касательной к кривой y = x ^ 2 — 7x + 3 в точке с абсциссой x = 1.

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Найдите угловой коэффициент касательной, проведенной к кривой у = 6 / х в точке х = 3 ?

Найдите угловой коэффициент касательной, проведенной к кривой у = 6 / х в точке х = 3 .

Вы открыли страницу вопроса Найдите уравнение кривой, проходящей через точку М ( — 1 ; 3), если угловой коэффициент касательной в любой точке кривой равен утроенному квадрату абсциссы точки касания?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Видео:Угловой коэффициент прямой. Решение задач.Скачать

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

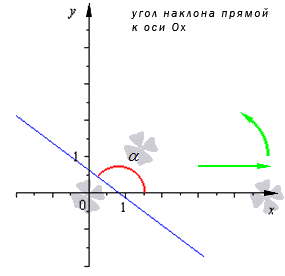
Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Видео:№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

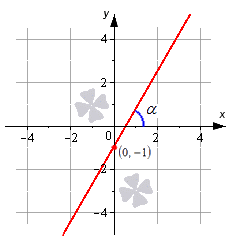
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

💡 Видео

Как найти угловой коэффициент прямой. На что влияет угловой коэффициент. Урок 7. Геометрия 8-9 классСкачать

Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Угловой коэффициент прямой. Пример 3Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

9 класс, 7 урок, Уравнение прямойСкачать