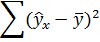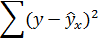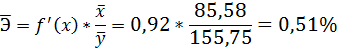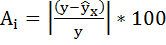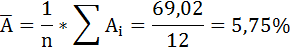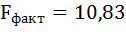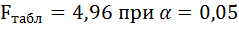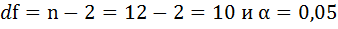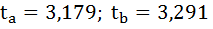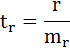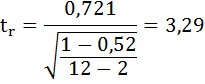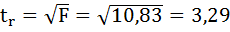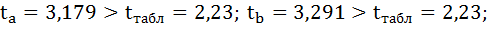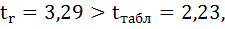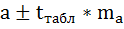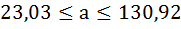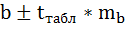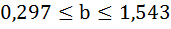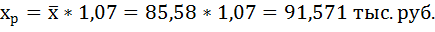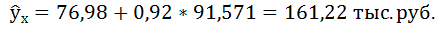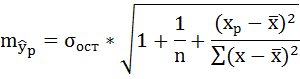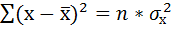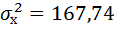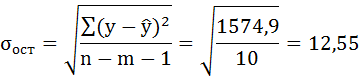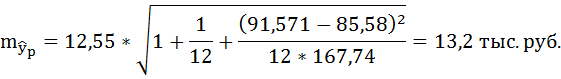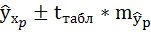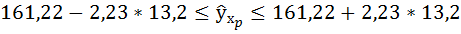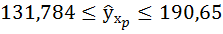- Методы расчета коэффициента корреляции
- Формула расчета коэффициента корреляции
- Пример расчета коэффициента корреляции
- Онлайн калькулятор расчета коэффициента корреляции
- Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
- Задание:
- Решение:
- Корреляционный анализ в Excel. Пример выполнения корреляционного анализа
- Суть корреляционного анализа
- Назначение корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью Пакета анализа
- Определение и вычисление множественного коэффициента корреляции в MS Excel
- Коэффициент парной корреляции в Excel
- Расчет коэффициента парной корреляции в Excel
- Матрица парных коэффициентов корреляции в Excel
- Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
- Примеры использования функции КОРРЕЛ в Excel
- Определение коэффициента корреляции влияния действий на результат
- Анализ популярности контента по корреляции просмотров и репостов видео
- Особенности использования функции КОРРЕЛ в Excel
- Оценка статистической значимости коэффициента корреляции
- Заключение
- 📹 Видео
Видео:Корреляционно-регрессионный анализ. Функциональная и корреляционная связиСкачать
Методы расчета коэффициента корреляции
При изучении различных социально-экономических явлений выделяют функциональную связь и стохастическую зависимость. Функциональная связь — это такой вид связи, при которой некоторому взятому значению факторного показателя соответствует лишь одно значение результативного показателя. Функциональная связь проявляется во всех случаях исследования и для каждой определенной единицы анализируемой совокупности.
Размещено на www.rnz.ru
В том случае, когда причинная зависимость действует не в каждом конкретном случае, а в общем для всей наблюдаемой совокупности, среднем при значительном количестве наблюдений, то такая зависимость является стохастической. Частным случаем стохастической зависимости выступает корреляционная связь, при которой изменение средней величины результативного показателя вызвано изменением значений факторных показателей. Расчет степени тесноты и направления связи выступает значимой задачей исследования и количественной оценки взаимосвязи различных социально-экономических явлений. Определение степени тесноты связи между различными показателями требует определение уровня соотношения изменения результативного признака от изменения одного (в случае исследования парных зависимостей) либо вариации нескольких (в случае исследования множественных зависимостей) признаков-факторов. Для определения такого уровня используется коэффициент корреляции.
Линейный коэффициент корреляции был впервые введен в начале 90-х гг. XIX в. Пирсоном и показывает степень тесноты и направления связи между двумя коррелируемыми факторами в случае, если между ними имеется линейная зависимость. При интерпретации получаемого значения линейного коэффициента корреляции степень тесноты связи между признаками оценивается по шкале Чеддока, один из вариантов этой шкалы приведен в нижеследующей таблице:
Шкала Чеддока количественной оценки степени тесноты связи
| Величина показателя тесноты связи | Характер связи |
|---|---|
| До |±0,3| | Практически отсутствует |
| |±0,3|-|±0,5| | Слабая |
| |±0,5|-|±0,7| | Умеренная |
| |±0,7|-|±1,0| | Сильная |
При интерпретации значения коэффициента линейной корреляции по направлению связи выделяют прямую и обратную. В случае наличия прямой связи с повышением или снижением величины факторного признака происходит повышение или снижение показателей результативного признака, т.е. изменение фактора и результата происходит в одном направлении. Например, повышение величины прибыли способствует росту показателей рентабельности. При наличии обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с динамикой факторного признака. Например, с повышением производительности труда уменьшается себестоимость единицы выпускаемой продукции и т.п.
Видео:Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать

Формула расчета коэффициента корреляции
В теории разработаны и на практике применяются различные модификации формул для расчета данного коэффициента. Общая формула для расчета коэффициента корреляции имеет следующий вид:

где r — линейный коэффициент корреляции.
Опираясь на математические свойства средней, общую формулу можно представить следующим образом, получив следующее выражение:
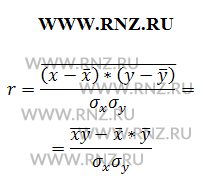
Выполняя дальнейшие преобразование, можно получить следующие формулы вычисления коэффициента корреляции Пирсона:
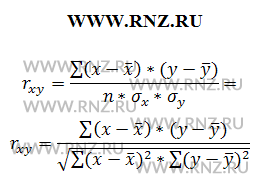
где n — число наблюдений.
Выполняя вычисление по итоговым данным для расчета показателя корреляции, его можно рассчитать с использованием следующих формул:
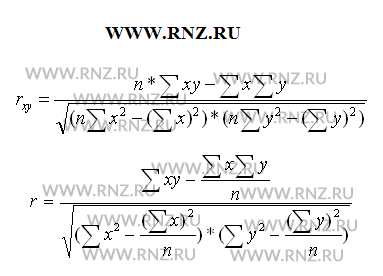
Методом расчета показателя корреляции является вычисление данного показателя с использованием его взаимосвязи с дисперсиями факторного и результативного признаков по следующей формуле:

Последние три приведенные формулы используются для изучения взаимосвязи между признаками в совокупностях незначительной величины — до 30 наблюдений.
Также показатель тесноты связи можно определить на основе его взаимосвязи с показателями уравнения регрессии, используя следующее отношение:
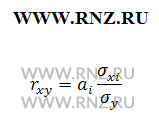
где аi — коэффициент регрессии в уравнении связи;
σхi — среднее квадратическое отклонение соответствующего статистически существенного факторного признака.
Линейный коэффициент корреляции несет в себе важную информацию для успешного изучения социально-экономических явлений и процессов, распределение которых близко к нормальному. Теоретически является обоснованным, что условие rxy = 0 является необходимым и достаточным для того, чтобы факторный и результативный признаки x и y являлись независимыми. При указанном условии, когда показатель корреляции равен нулю, показатели регрессии также имеют нулевые значения, а прямые линии регрессии у по х и х по у являются взаимно перпендикулярными на графике (параллельными: одна прямая — оси х, а другая прямая — оси y).
В том случае, когда rxy = 1, то это означает, что все точки (х, у) расположены на прямой и зависимость между х и у относится к функциональным. При указанном условии прямые линии регрессии совпадают. Указанное положение действует также в случае исследования трех и более показателей, если они подчинены закону нормального распределения.
В целом значение линейного показателя связи находится в диапазоне от — 1 до 1, т.е.: -1
Видео:Математика #1 | Корреляция и регрессияСкачать

Пример расчета коэффициента корреляции
Приведем пример расчета коэффициента корреляции Пирсона для значений, приведенных в следующей таблице. Для этого используем следующие данные (пример условный):
| Значение показателя X | Значение показателя Y |
|---|---|
| 1,1 | 1,3 |
| 1,9 | 1,1 |
| 1,5 | 1,2 |
| 1,9 | 0,5 |
| 1,9 | 1,5 |
| 1,1 | 1,7 |
| 0,9 | 2 |
| 1 | 0,9 |
| 1,3 | 1,2 |
| 1,5 | 1,7 |
Количество наблюдений менее 30, поэтому в нашем примере для расчета парного коэффициента корреляции используем следующую формулу:
Для этого составим вспомогательную таблицу:
| № п/п | X | Y | xy | x 2 | y 2 |
|---|---|---|---|---|---|
| 1 | 1,1 | 1,3 | 1,43 | 1,21 | 1,69 |
| 2 | 1,9 | 1,1 | 2,09 | 3,61 | 1,21 |
| 3 | 1,5 | 1,2 | 1,8 | 2,25 | 1,44 |
| 4 | 1,9 | 0,5 | 0,95 | 3,61 | 0,25 |
| 5 | 1,9 | 1,5 | 2,85 | 3,61 | 2,25 |
| 6 | 1,1 | 1,7 | 1,87 | 1,21 | 2,89 |
| 7 | 0,9 | 2 | 1,8 | 0,81 | 4 |
| 8 | 1 | 0,9 | 0,9 | 1 | 0,81 |
| 9 | 1,3 | 1,2 | 1,56 | 1,69 | 1,44 |
| 10 | 1,5 | 1,7 | 2,55 | 2,25 | 2,89 |
| Итого | 14,1 | 13,1 | 17,8 | 21,25 | 18,87 |
Методология вычисления: r = (17,8-14,1*13,1/10)/(√((21,25-14,1*14,1/10)*(18,87-13,1*13,1/10))) = -0,4389.
Полученное значение коэффициента корреляции Пирсона говорит о наличии обратной связи между X и Y. Величина коэффициента корреляции Пирсона показывает, что связь между X и Y слабая.
Видео:Теория вероятностей #19: ковариация, корреляция, зависимость двух случайных величинСкачать

Онлайн калькулятор расчета коэффициента корреляции
В заключении приводим небольшой онлайн калькулятор расчета коэффициента корреляции онлайн, используя который, Вы можете самостоятельно выполнить расчет значения коэффициента корреляции Пирсона и получить интерпретацию рассчитанного значения. При заполнении формы калькулятора внимательно соблюдайте размерность полей, что позволит выполнить расчет коэффициента корреляции онлайн быстро и точно. В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как это работает. Для определения значения показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить вычисления». При заполнении формы соблюдайте размерность показателей! Дробные числа записываются с точной, а не запятой!
Онлайн-калькулятор расчета коэффициента корреляции:
Видео:Эконометрика. Линейная парная регрессияСкачать

Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
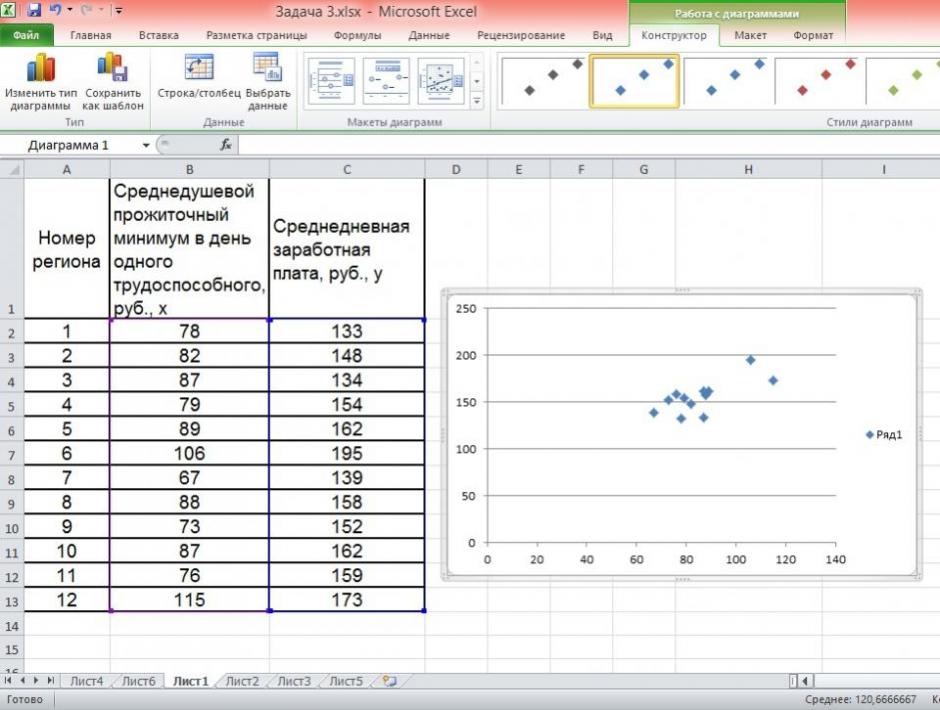
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
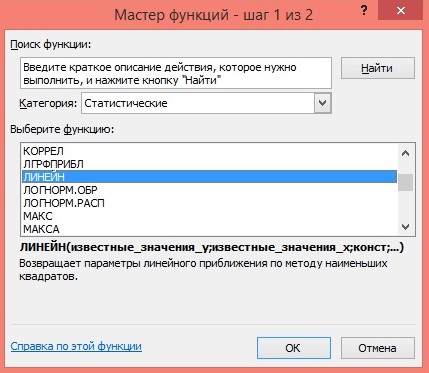
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
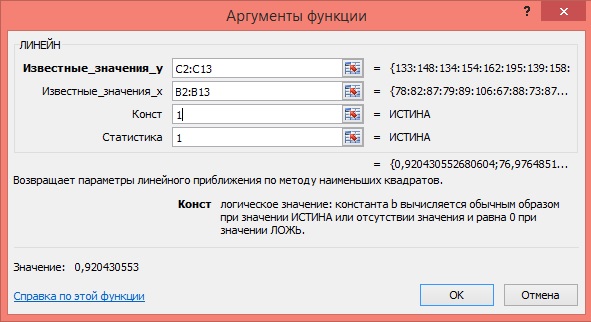
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
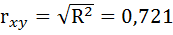
Связь оценивается как тесная.
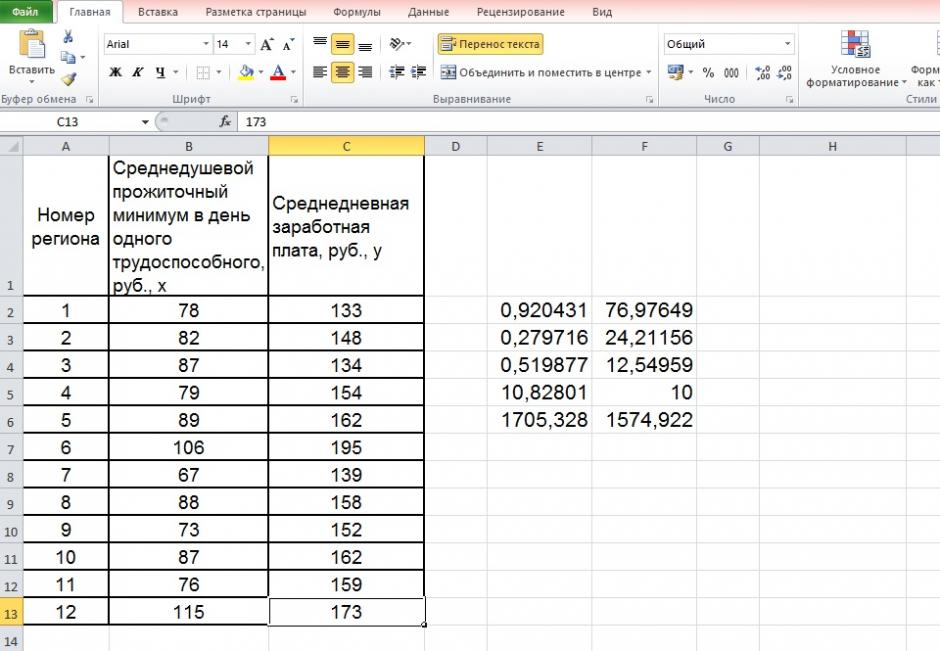
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 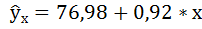
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
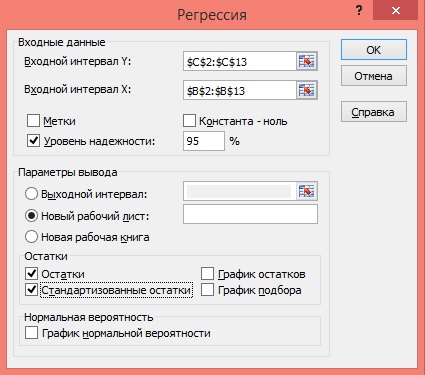
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
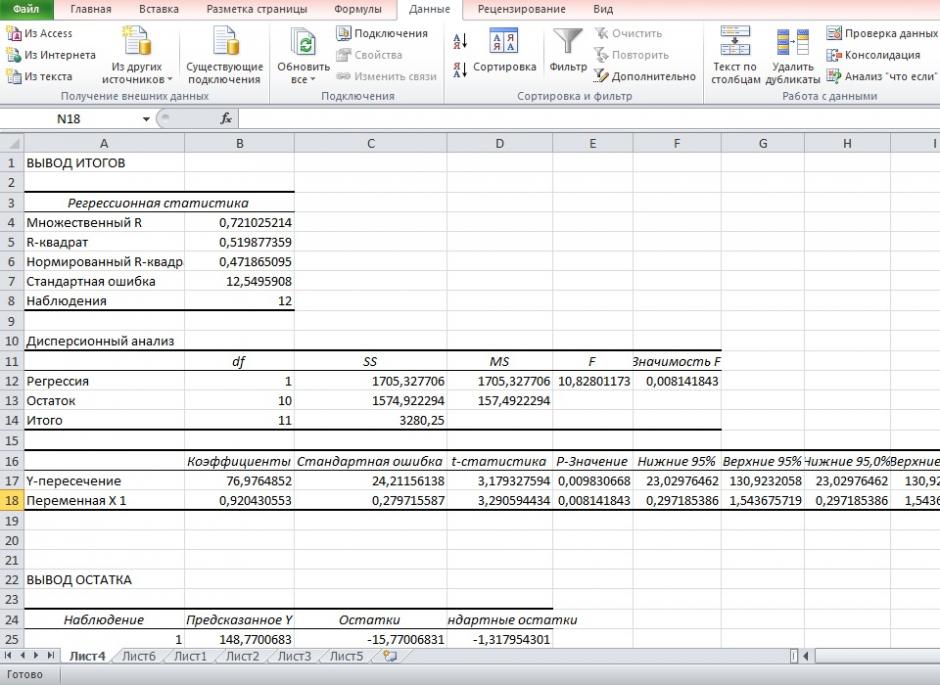
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
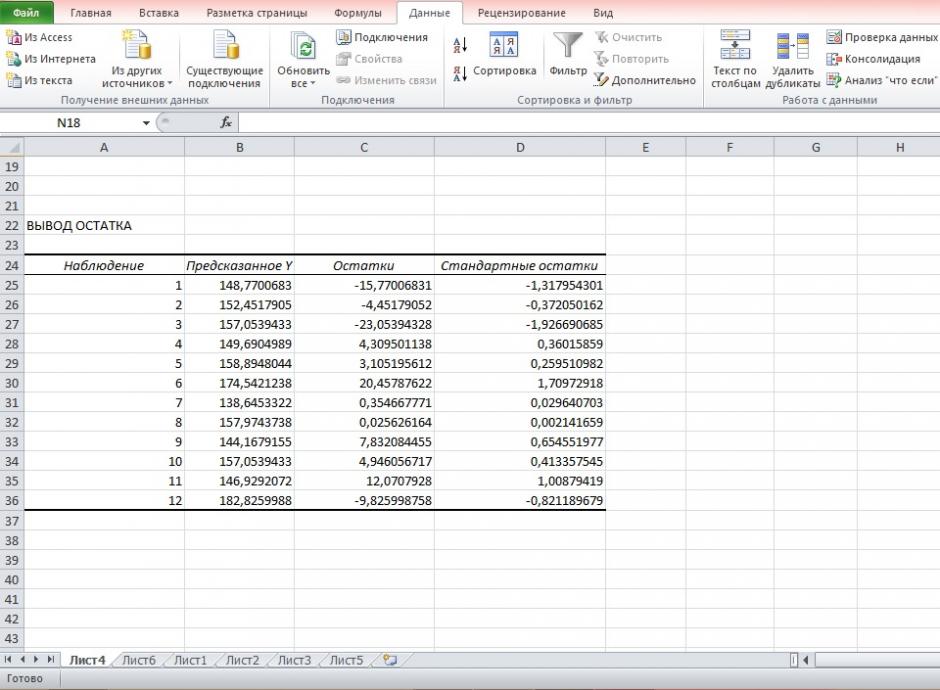
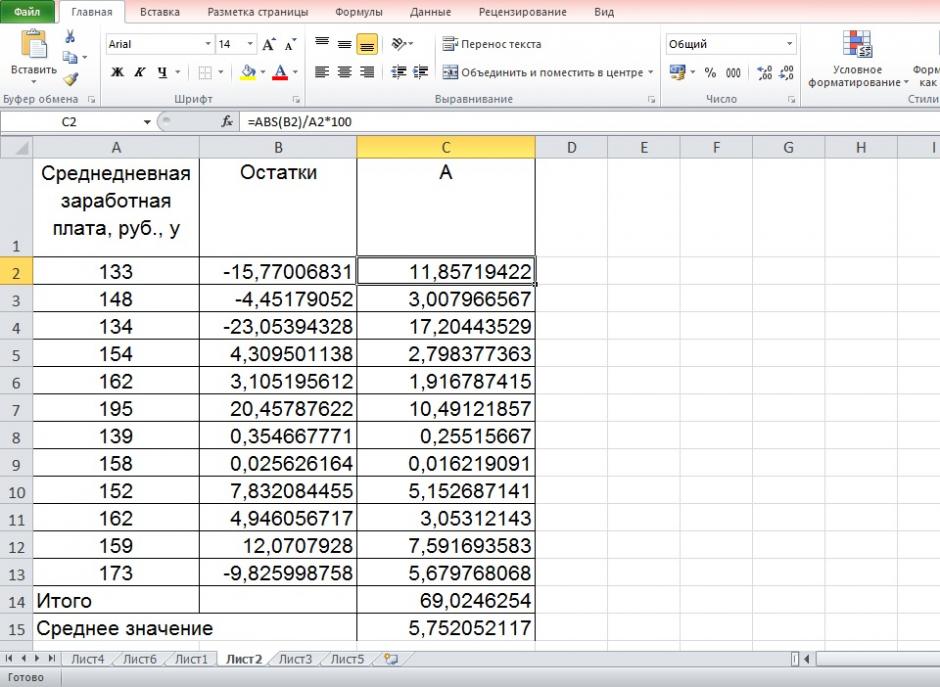
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 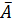
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 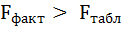
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
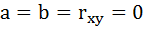
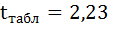
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где 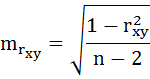
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 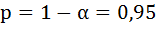
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
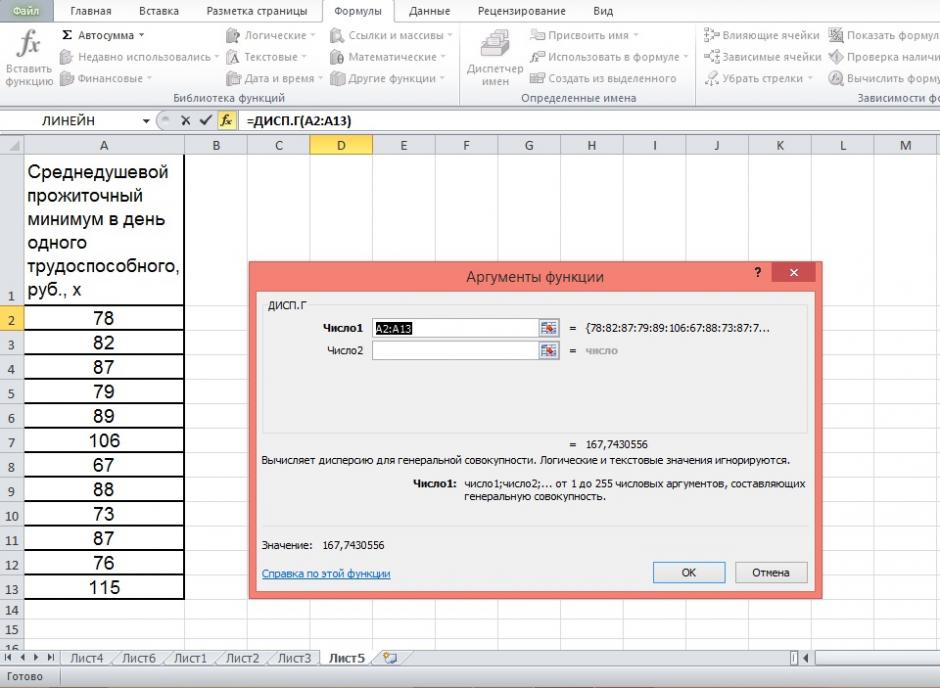
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 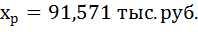
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
Видео:Расчет коэффициента корреляции в ExcelСкачать

Корреляционный анализ в Excel. Пример выполнения корреляционного анализа
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Видео:Как вычислить линейный коэффициент корреляции по таблице? Корреляционное поле и прямая регрессииСкачать

Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Видео:Корреляционная связь Статобработка NmСкачать

Назначение корреляционного анализа
Зависимость устанавливается тогда, когда начинается выявление коэффициента корреляции. Этот метод отличается от анализа регрессии, так как здесь только один показатель, рассчитываемый при помощи корреляции. Интервал изменяется от +1 до -1. Если она плюсовая, то повышение первой величины способствует повышению 2-й. Если минусовая, то повышение 1-й величины способствует понижению 2-й. Чем выше коэффициент, тем сильнее одна величина влияет на 2-ю.
Важно! При 0-м коэффициенте зависимости между величинами нет.
Видео:Парная регрессия: линейная зависимостьСкачать

Расчет коэффициента корреляции
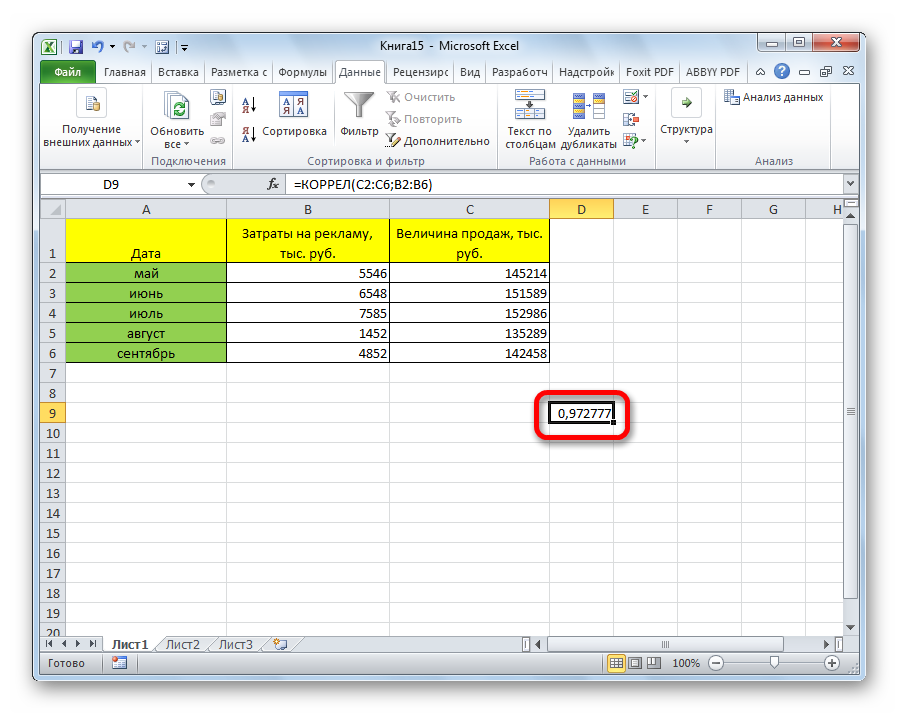
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
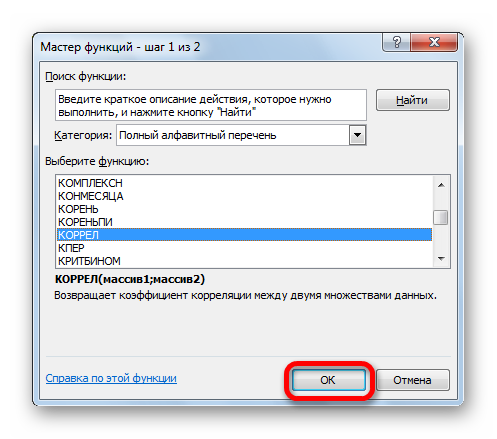
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид — КОРРЕЛ(массив1;массив2). Подробная инструкция:
- Необходимо произвести выделение ячейки, в которой планируется выводить итог расчета. Нажать «Вставить функцию», находящуюся слева от текстового поля для ввода формулы.
1
- Открывается «Мастер функций». Здесь необходимо найти КОРРЕЛ, кликнуть на нее, затем на «ОК».
- Открылось окошко аргументов. В строку «Массив1» необходимо ввести координаты интервалы 1-го из значений. В рассматриваемом примере — это столбец «Величина продаж». Нужно просто произвести выделение всех ячеек, которые находятся в этой колонке. В строку «Массив2» аналогично необходимо добавить координаты второй колонки. В рассматриваемом примере — это столбец «Затраты на рекламу».
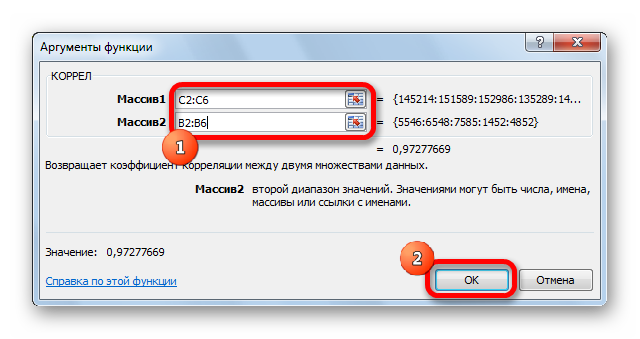
- После введения всех диапазонов кликаем на кнопку «ОК».
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
- Переходим в раздел «Файл».
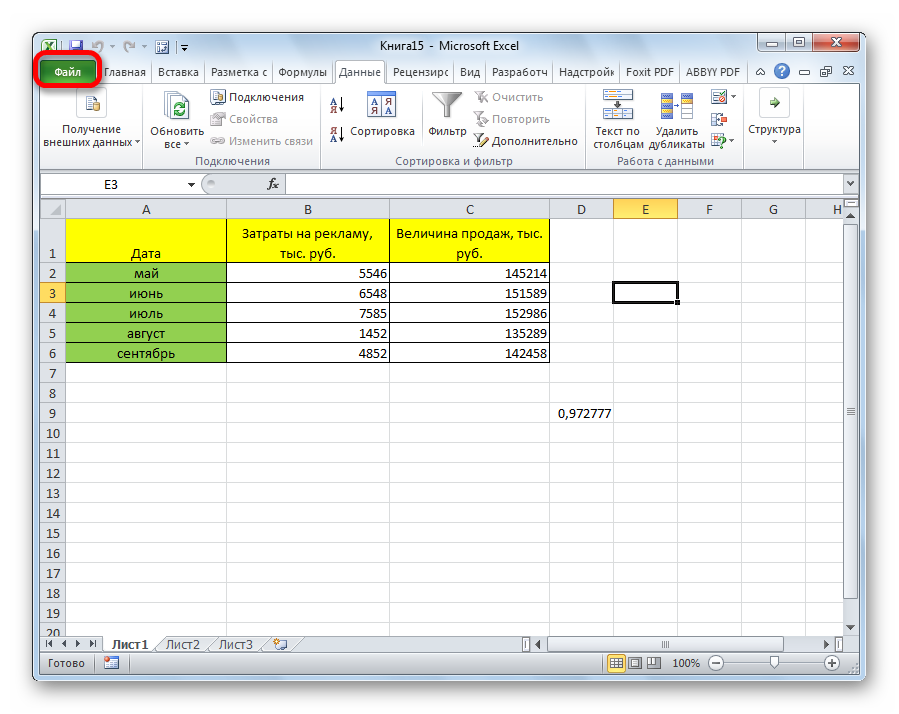
- Открылось новое окошко, в котором нужно кликнуть на раздел «Параметры».
- Жмём на «Надстройки».
- Находим в нижней части элемент «Управление». Здесь необходимо выбрать из контекстного меню «Надстройки Excel» и кликнуть «ОК».
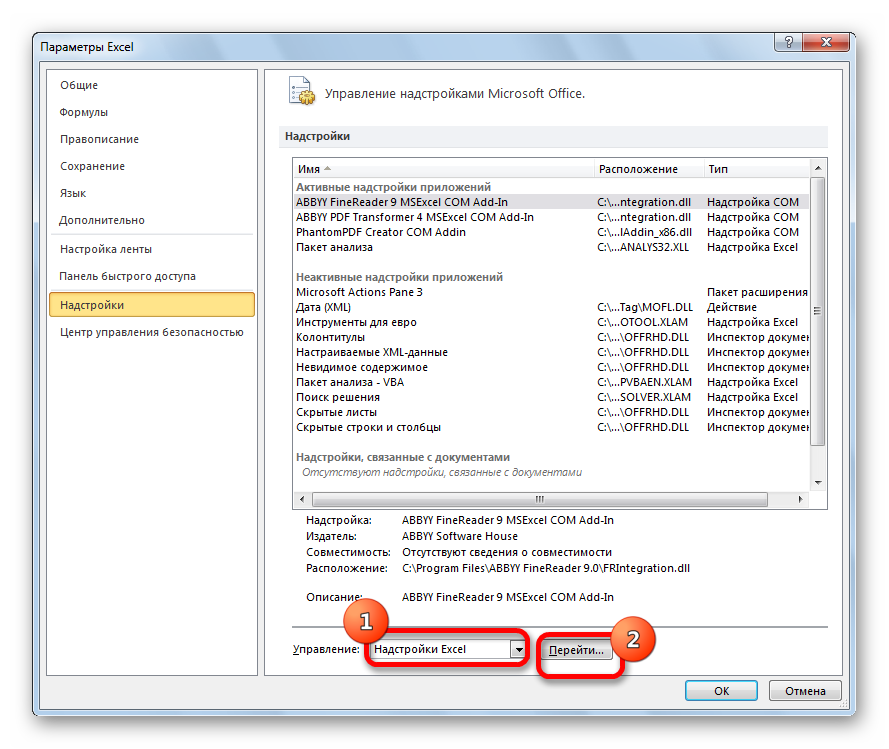
- Открылось специальное окно надстроек. Ставим галочку рядом с элементом «Пакет анализа». Кликаем «ОК».
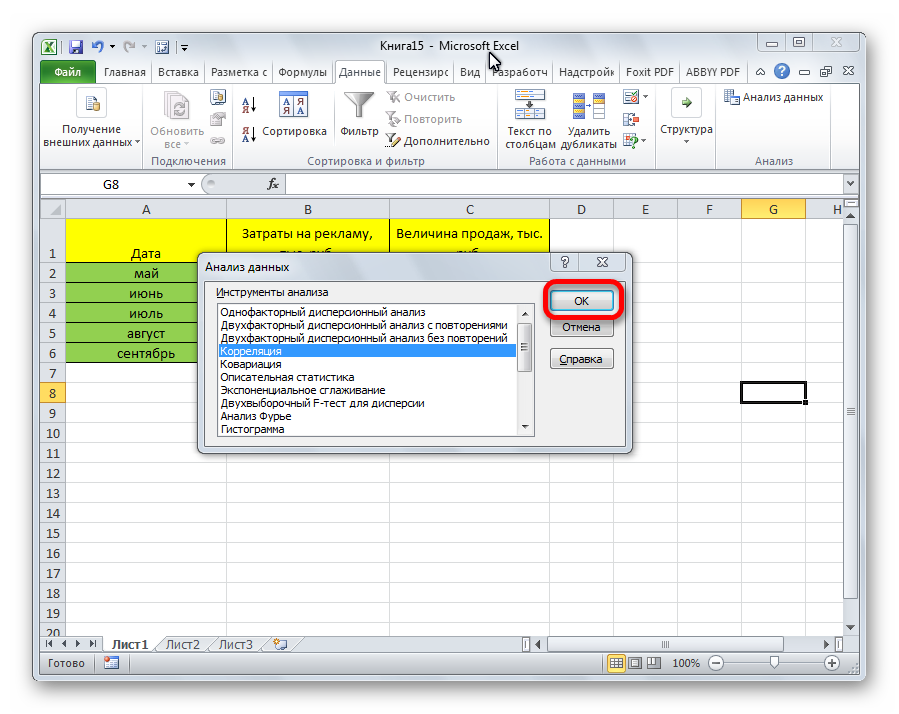
- Активация прошла успешно. Теперь переходим в «Данные». Появился блок «Анализ», в котором необходимо кликнуть «Анализ данных».
- В новом появившемся окошке выбираем элемент «Корреляция» и жмем на «ОК».
- На экране появилось окошко настроек анализа. В строчку «Входной интервал» необходимо ввести диапазон абсолютно всех колонок, принимающих участие в анализе. В рассматриваемом примере — это столбики «Величина продаж» и «Затраты на рекламу». В настройках отображения вывода изначально выставлен параметр «Новый рабочий лист», что означает показ результатов на другом листе. По желанию можно поменять локацию вывода результата. После проведения всех настроек нажимаем на «ОК».
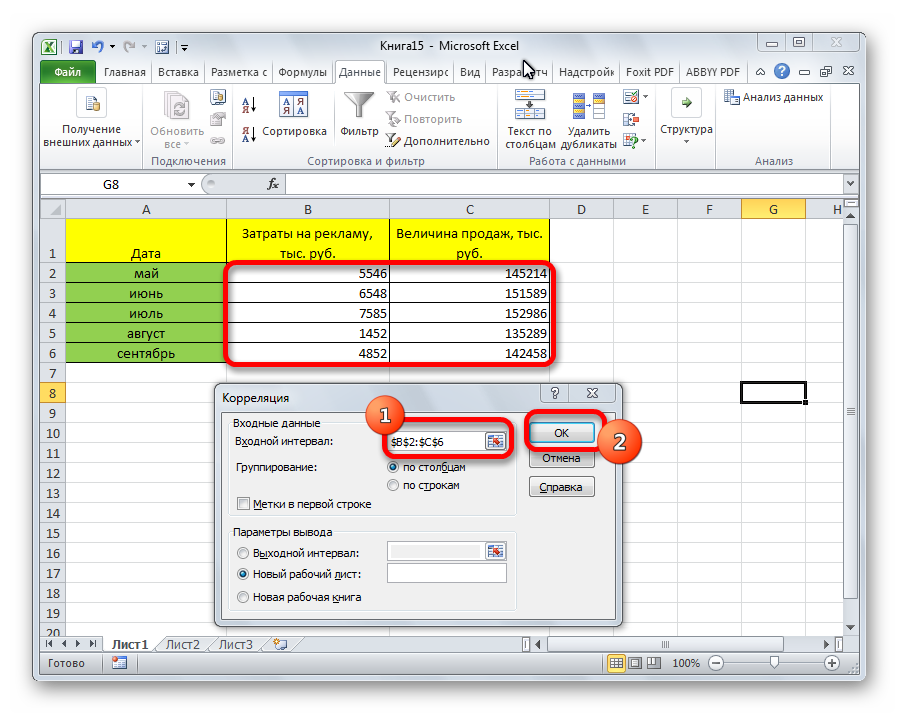
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Видео:Эконометрика Линейная регрессия и корреляцияСкачать

Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
- В разделе «Данные» находим уже известный блок «Анализ» и жмем «Анализ данных».
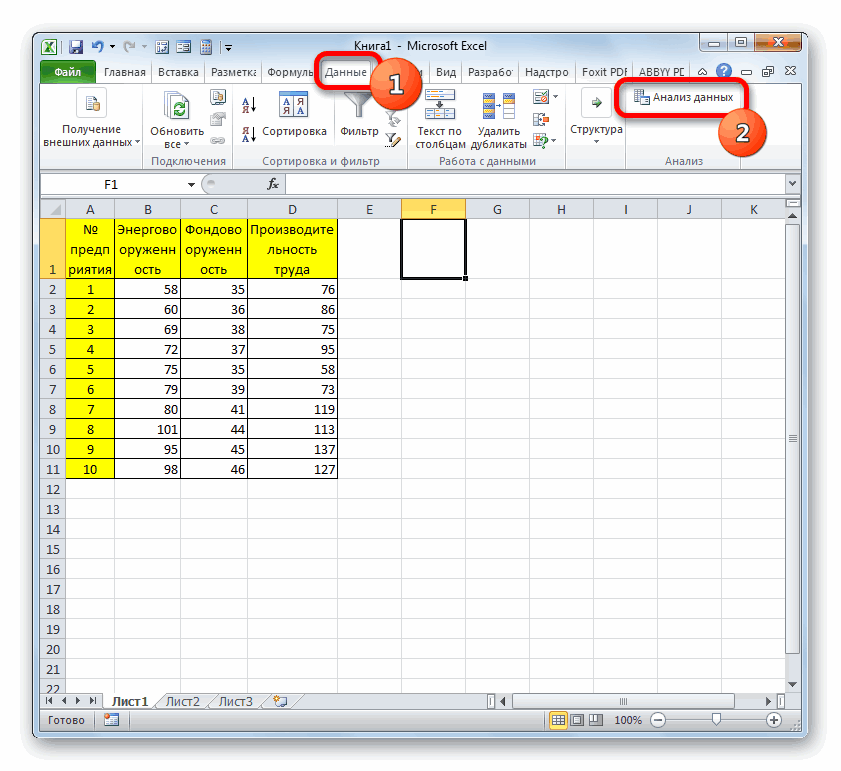
- В отобразившемся окошке жмем на элемент «Корреляция» и кликаем на «ОК».
- В строку «Входной интервал» вбиваем интервал по трём или более столбцам исходной таблицы. Диапазон можно ввести вручную или же просто выделить его ЛКМ, и он автоматически отобразится в нужной строчке. В «Группирование» выбираем подходящий способ группировки. В «Параметр вывода» указывает место, в которое будут выведены результаты корреляции. Кликаем «ОК».
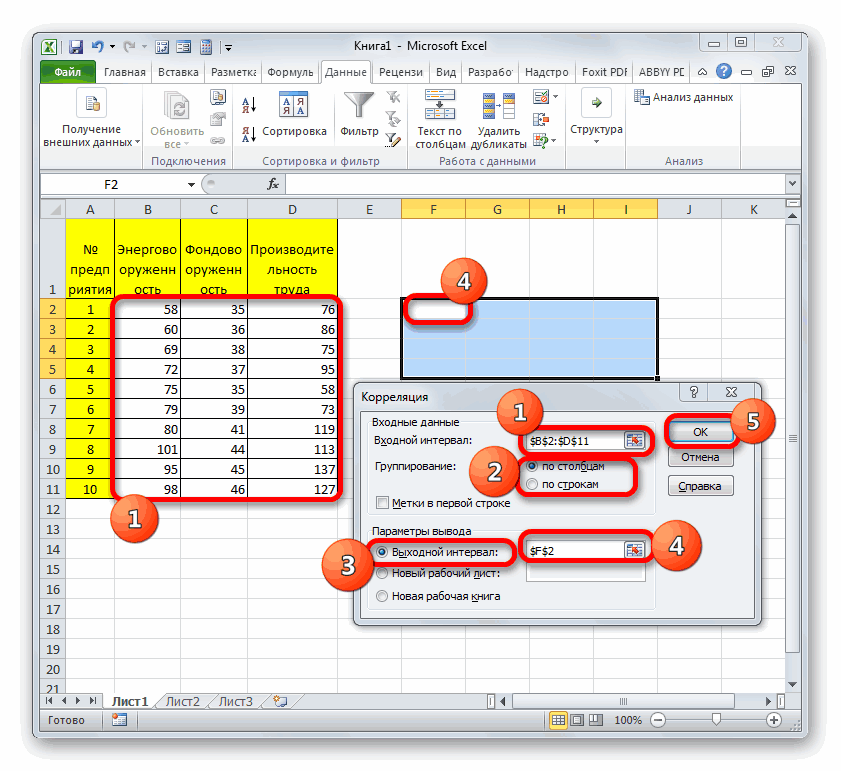
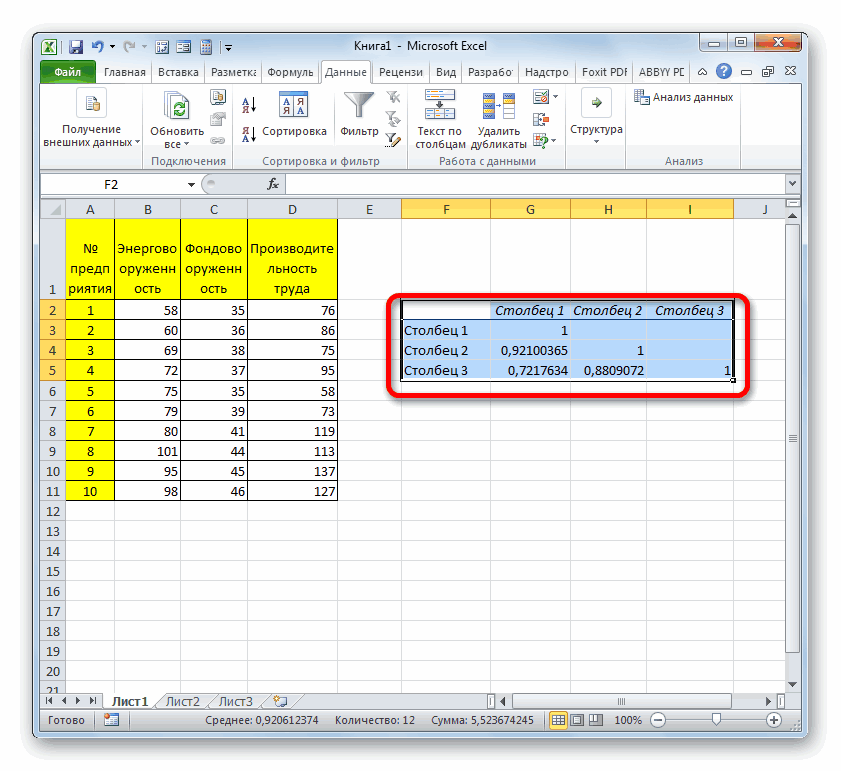
- Готово! Построилась матрица корреляции.
Видео:Коэффициент корреляции Пирсона в ExcelСкачать

Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
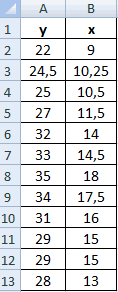
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
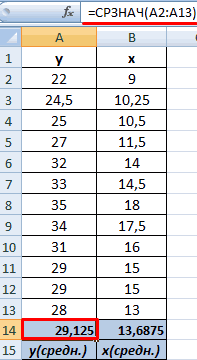
- Выявим средние показатели величин при помощи функции СРЗНАЧ.
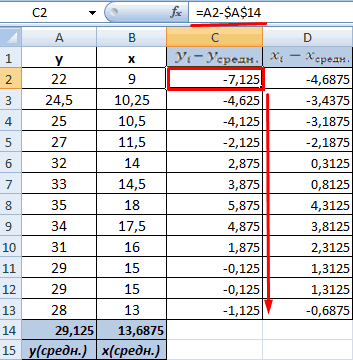
- Произведем расчет каждого х и хсредн, у и усредн при помощи оператора «-».
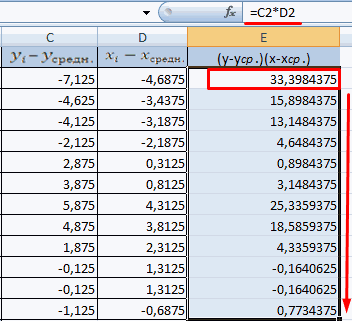
- Производим перемножение вычисленных разностей.
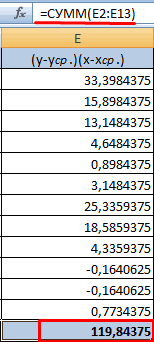
- Вычисляем сумму показателей в этом столбце. Числитель – найденный результат.
- Посчитаем знаменатели разницы х и х-средн, у и у-средн. Для этого произведем возведение в квадрат.
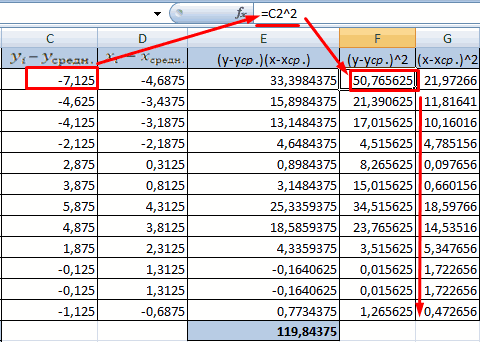
- Используя функцию АВТОСУММА, найдем показатели в полученных столбиках. Производим перемножение. При помощи функции КОРЕНЬ возводим результат в квадрат.
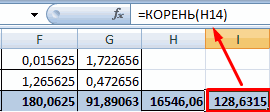
- Производим подсчет частного, используя значения знаменателя и числителя.
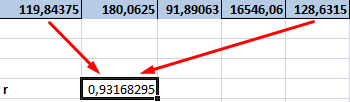
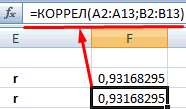
- КОРРЕЛ – интегрированная функция, которая позволяет предотвратить проведение сложнейших расчетов. Заходим в «Мастер функций», выбираем КОРРЕЛ и указываем массивы показателей х и у. Строим график, отображающий полученные значения.
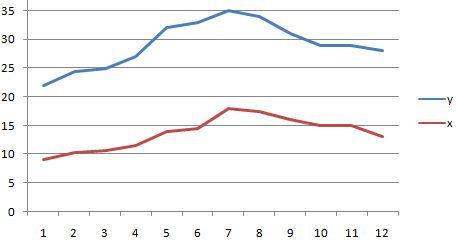
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
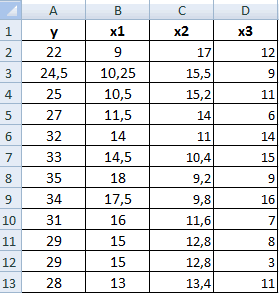
- Заходим в «Анализ данных», находящийся в блоке «Анализ» вкладки «Данные». В отобразившемся списке выбираем «Корелляция».
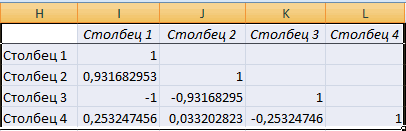
- Выставляем все необходимые настройки. «Входной интервал» – интервал всех четырех колонок. «Выходной интервал» – место, в котором желаем отобразить итоги. Кликаем на кнопку «ОК».
- В выбранном месте построилась матрица корреляции. Каждое пересечение строки и столбца – коэффициенты корреляции. Цифра 1 отображается при совпадающих координатах.
Видео:Множественная регрессия в ExcelСкачать

Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
Первый пример. Есть табличка, в которой расписана информация об усредненных показателях заработной платы работников компании на протяжении одиннадцати лет и курсе $. Необходимо выявить связь между этими 2-умя величинами. Табличка выглядит следующим образом:
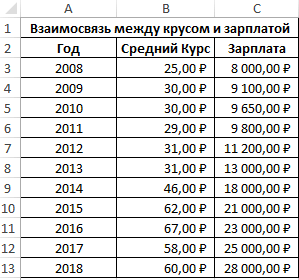
Алгоритм расчёта выглядит следующим образом:
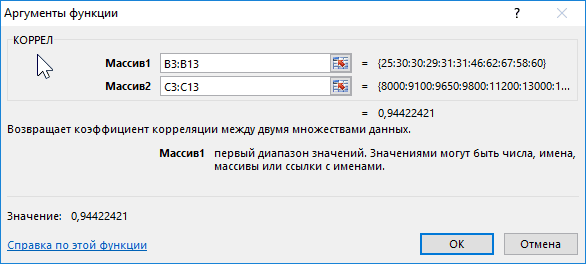
Отображенный показатель близок к 1. Результат:
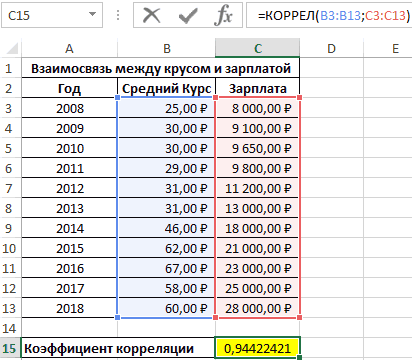
Определение коэффициента корреляции влияния действий на результат
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
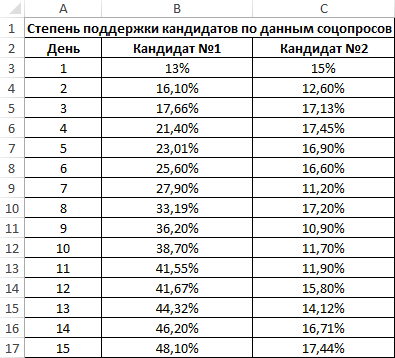
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
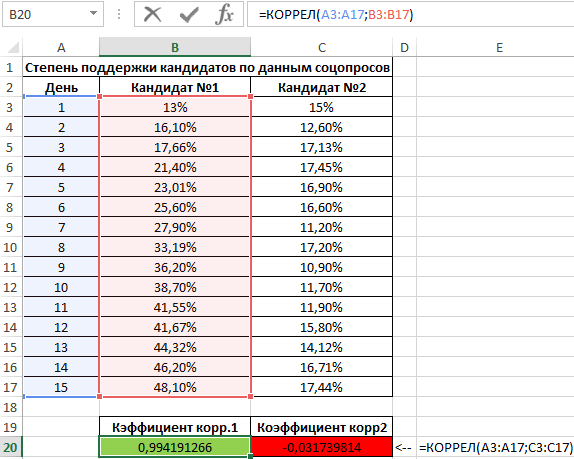
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
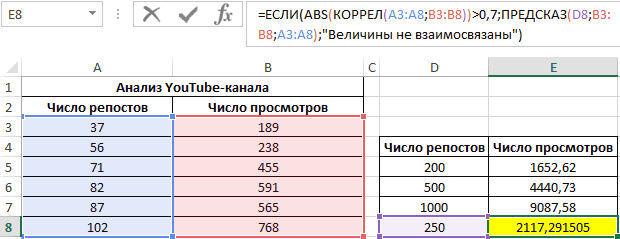
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
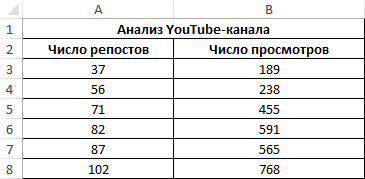
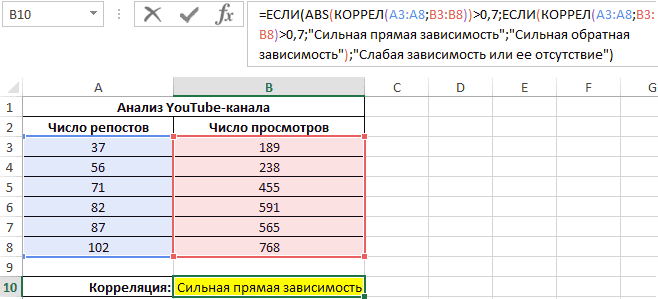
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;»Сильная прямая зависимость»;»Сильная обратная зависимость»);»Слабая зависимость или ее отсутствие»)’ >
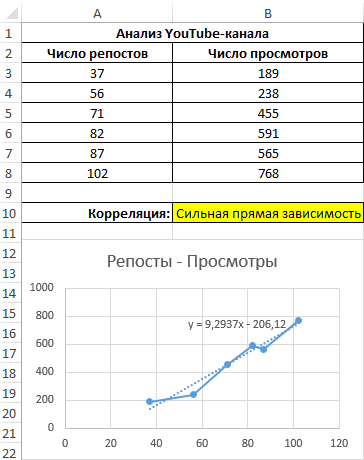
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
Теперь производим построение графика:
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
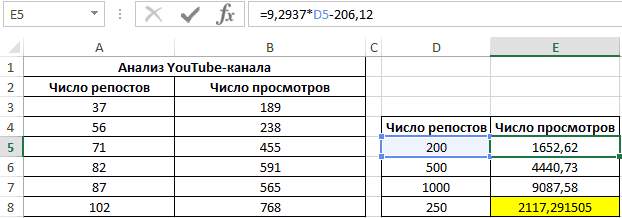
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);»Величины не взаимосвязаны»)’ >. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
- Не учитываются ячейки пустого типа.
- Не учитываются ячейки, в которых находится информация типа Boolean и Text.
- Двойное отрицание «—» применяется для учёта логических величин в виде чисел.
- Количество ячеек в исследуемых массивах обязаны совпадать, иначе будет выведено сообщение #Н/Д.
Видео:Коэффициент корреляции. Статистическая значимостьСкачать

Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
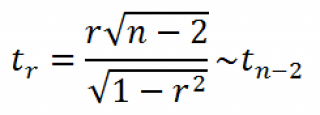
Видео:Корреляция: коэффициенты Пирсона и Спирмена, линейная регрессияСкачать

Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
📹 Видео
Эконометрика. Множественная регрессия и корреляция.Скачать

Корреляционный анализ Спирмена. Коэффициент корреляции Спирмена. КОРРЕЛЯЦИЯ. АНАЛИЗ ДАННЫХ.Скачать

Лекция 7. Корреляционный анализСкачать

6. Связь между количественными показателямиСкачать

КорреляцияСкачать

Тема 3. Анализ парной связи. Корреляционный анализСкачать