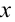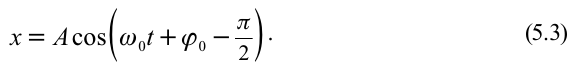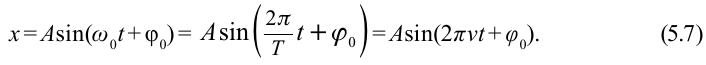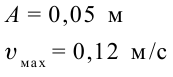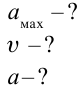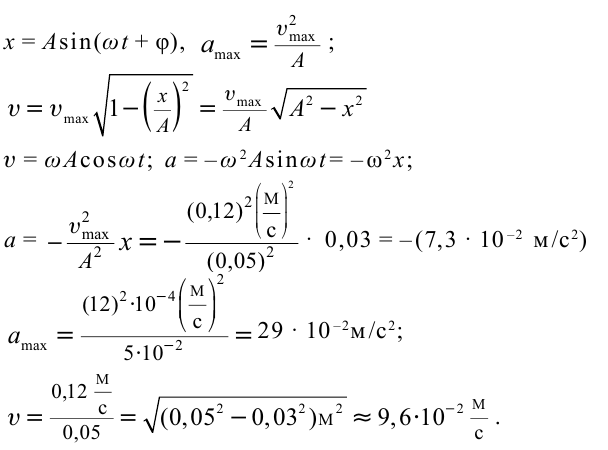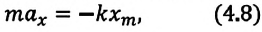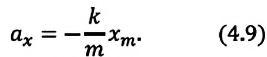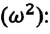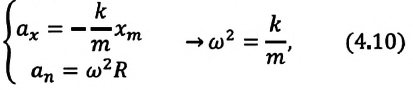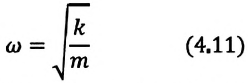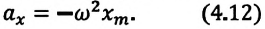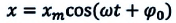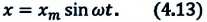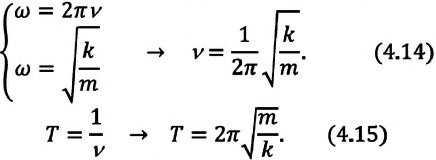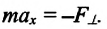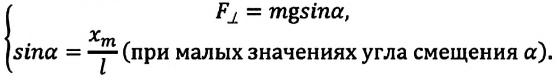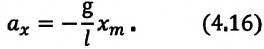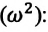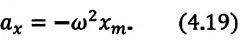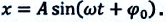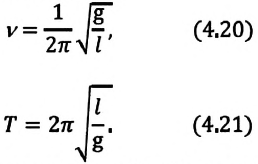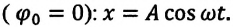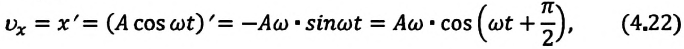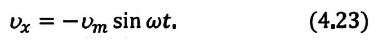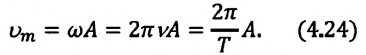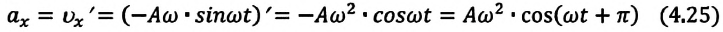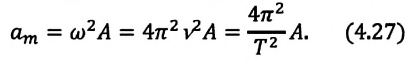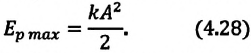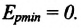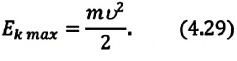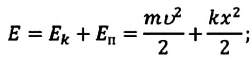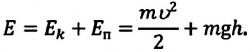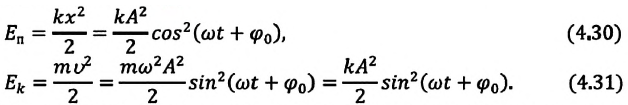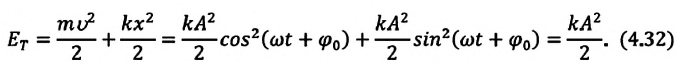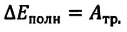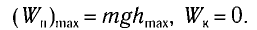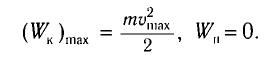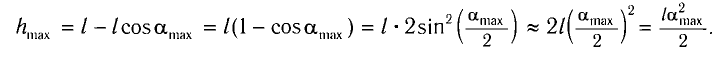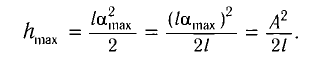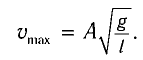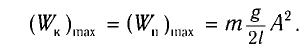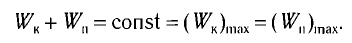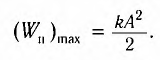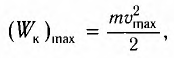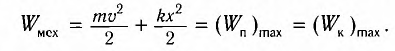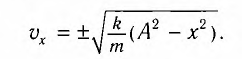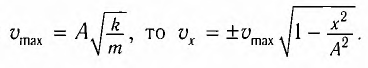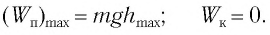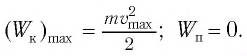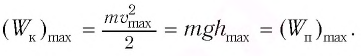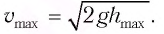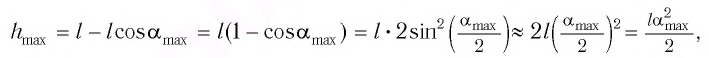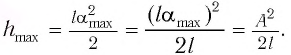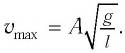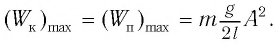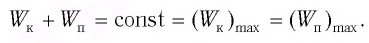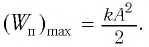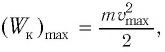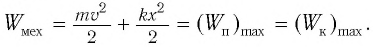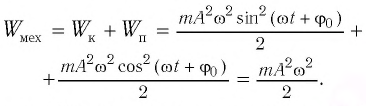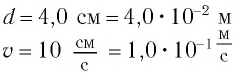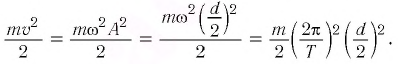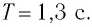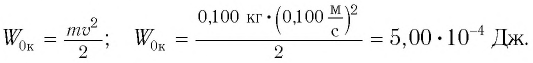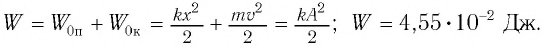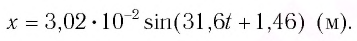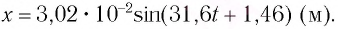Уравнение координаты скорости и ускорения для гармонических

Видео:Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

Тестирование онлайн

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Видео:Физика - уравнения равноускоренного движенияСкачать

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Видео:Урок 327. Гармонические колебанияСкачать

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:Выполнялка 53.Гармонические колебания.Скачать

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:5.4 Уравнение гармонических колебанийСкачать

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Уравнение гармонических колебаний

п.1. Гармонические колебания как простейший периодический процесс

Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.

Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10 -14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·10 15 с

Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sin⁡t) и (cos⁡t) с периодом (T=2pi).

Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:

Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac=4pi text end Получаем закон колебаний: (x(t)=5cos(4pi t))

п.2. Перемещение, скорость и ускорение при гармоническом движении

Пусть (x(t)) — координата тела, участвующего в периодическом движении по закону: $$ x(t)=Acos⁡omega t $$ Найдем скорость как первую производную от координаты: $$ v(t)=x'(t)=-Aomega sinomega t=Aomega cos⁡left(omega t+fracpi 2right) $$ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $$ v_m=Aomega $$ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $$ a(t)=v'(t)=x»(t)=-Aomega^2 cosomega t=Aomega^2 cos⁡(omega t+pi) $$ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $$ a_m=Aomega^2 $$ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:

Из уравнения для ускорения получаем: $$ x»(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $$ Откуда следует:

Решением этого уравнения в общем виде будут: $$ x(t)=Asin⁡(omega t+varphi_0) text x(t)=A cos⁡(omega t+varphi_0) $$ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.

п.3. Примеры

Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?

Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения.

По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end Уравнение движения грузика: $$ x»(t)+frac km x(t)=0 $$ что является уравнением гармонических колебаний с частотой: (omega=sqrt)
Общее решение уравнения: (x(t)=Acosleft(sqrt+varphi_0right))
Амплитудные значения скорости и ускорения: $$ v_m=Asqrt, a_m=Afrac km $$ Ответ: (omega=sqrt)

Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?

Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g.

Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?

LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем.

Напряжение на конденсаторе (U_C(t)=frac). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin U_c(t)=varepsilon_L(t)Rightarrow frac=-LI'(t)Rightarrow frac+LI'(t)=0 end Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin frac+LQ»(t)=0 end Получаем уравнение гармонических колебаний: $$ Q»(t)=fracQ(t)=0, omega=frac<sqrt> $$ Общее решение уравнения: (Q(t)=Q_m cosleft(frac<sqrt>t+varphi_0right))
Напряжение на конденсаторе: $$ U_C(t)=frac=fraccosleft(frac<sqrt>t+varphi_0right) $$ Амплитудное значение напряжения: (U_m=frac)
Ток как скорость изменения заряда: $$ I(t)=Q'(t)=-frac<sqrt>sinleft(frac<sqrt>t+varphi_0right)=frac<sqrt>cosleft(frac<sqrt>t+varphi_0+fracpi 2right) $$ Амплитудное значение тока: (I_m=frac<sqrt>)
Ток опережает колебания заряда и напряжения на (fracpi 2)

Видео:11 класс урок №3 Практическая работа №1Скачать

Гармонические колебания в физике — формулы и определение с примерами

Содержание:

Гармонические колебания:

Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.

Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (

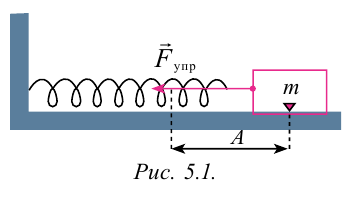
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 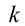, а ее масса ничтожна мала и можно ее не учитывать. Считаем, что масса системы сосредоточена в грузе, а упругость в пружине.

Если груз, который находится в равновесии, потянем вправо на расстояние 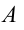и отпустим, то под действием силы упругость, которая появляется в пружине, груз смещается в
сторону равновесного состояния.

С течением времени смещение груза уменьшается относительно , но скорость груза при этом увеличивается. Когда груз доходит до равновесного состояния, его смещение () равняется нулю и соответственно сила упругости равняется нулю. Но груз по инерции начинает двигаться в левую сторону. Модуль силы упругости, которая появляется в пружине, тоже растет. Однако из-за того, что сила упругости постоянно направлена против смещения груза, она начинает тормозить груз. В результате движение груза замедляется, и, в результате, прекращается. Теперь груз под воздействием эластической силы сжатой пружины начинает двигаться в сторону равновесного состояния.
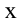
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде ():

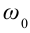
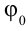
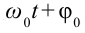
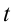
здесь: – циклическая частота, зависящая от параметров колеблющихся систем, – начальная фаза, () фаза колебания с течением времени .
Из математики известно, что 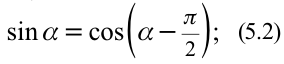поэтому формулу (5.2.) можно записать в виде

Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.

Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Основные параметры гармонических колебаний

a) период колебания 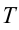– время одного полного колебания:

)

б) частота колебания 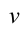– количество колебаний, совершаемых за 1 секунду:

Единица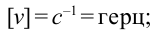
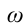
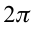
c) циклическая частота – количество колебаний за секунд:

С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.

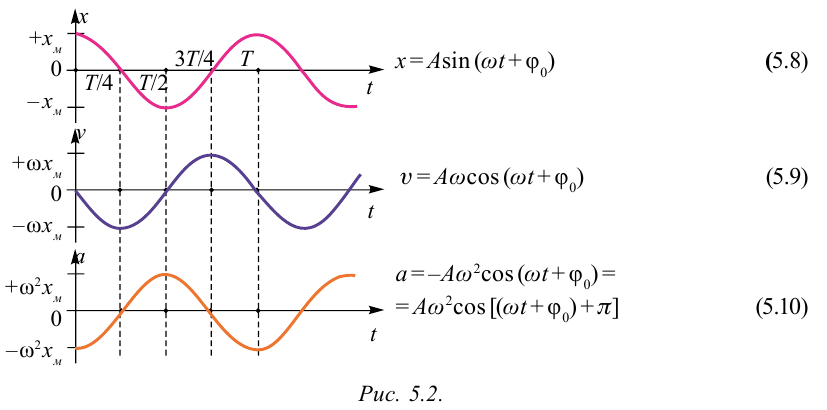
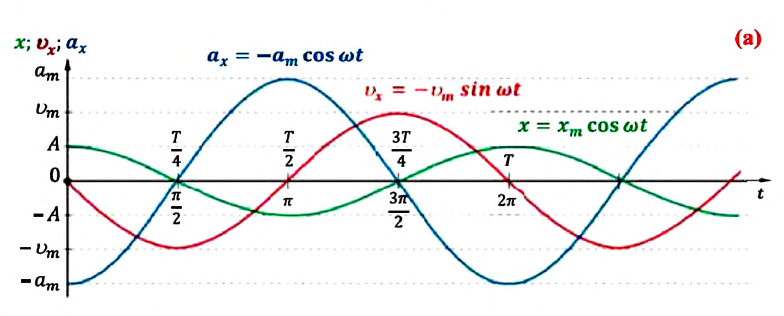
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:

Пример решения задачи:

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

Формула и решение:

Видео:Решение графических задач на равномерное движениеСкачать

Гармонические колебания пружинного маятника

В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.

Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:

Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.

Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.

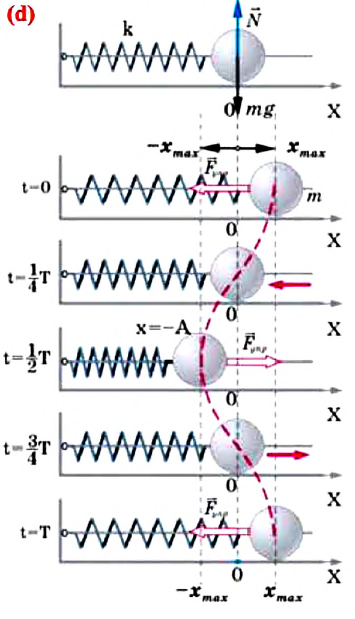
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).

В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 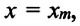сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:

Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.

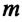
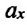
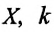
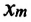
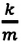
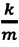
Где — масса шарика, закрепленного на пружине, — проекция ускорения шарика вдоль оси — жесткость пружины, -удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение — постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения — известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение соответствует квадрату циклической частоты

Таким образом, уравнение движения пружинного маятника можно записать и так:

Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 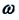являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:

Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.

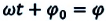
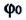
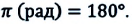
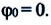
Здесь фаза колебания, — начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах: Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы В этом случае формулу гармонических колебаний пружинного маятника можно записать так:

или

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:

Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.

Видео:Уравнение движенияСкачать

Гармонические колебания математического маятника

До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.

Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.

Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.

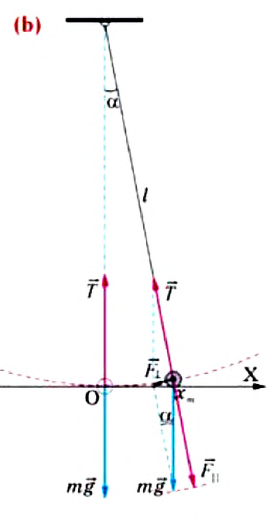
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).

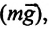
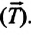
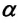
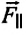
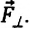
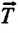
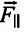
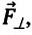
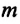
Сила тяжести действующая на шарик в положении равновесия маятника, уравновешивается силой натяжения нити Однако, если вывести маятник из состояния равновесия, сместив его на малый угол в сторону, то возникают две составляющие вектора силы тяжести -направленная вдоль нити и перпендикулярная нити Сила натяжения и составляющая силы тяжести уравновешивают друг друга. Поэтому равнодействующая сила будет равна составляющей «пытающейся» вернуть тело в положение равновесия (см.: рис. b). Учитывая вышеуказанное и ссылаясь на II закон Ньютона, можно написать уравнение колебательного движения тела массой в проекциях на ось ОХ:

Приняв во внимание, что:

Для уравнения движения математического маятника получим:

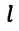
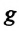
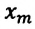
Где — длина математического маятника (нити), — ускорение свободного падения, — амплитуда колебания.

Для данной колебательной системы отношение — постоянная положительная величина, потому что ускорение свободного падения и длина нити не могут быть отрицательными. Если сравнить уравнения (4.16) и (4.10), с легкостью можно увидеть, что отношение также соответствует квадрату циклической частоты

Таким образом, уравнение движения математического маятника можно записать и так:

Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:

Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.

Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:

Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.

Скорость и ускорение при гармонических колебаниях

Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.

При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю

Так как скорость является первой производной смещения (координат) по времени, то:

Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 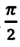(а).

Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:

Так как ускорение является первой производной скорости по времени, то получим:

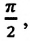
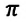
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на а колебания смещения на

(см.: рис. а). Максимальное (амплитудное) значение ускорения зависит от амплитуды, частоты и периода колебаний:

Превращения энергии при гармонических колебаниях

Теоретический материал

Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.

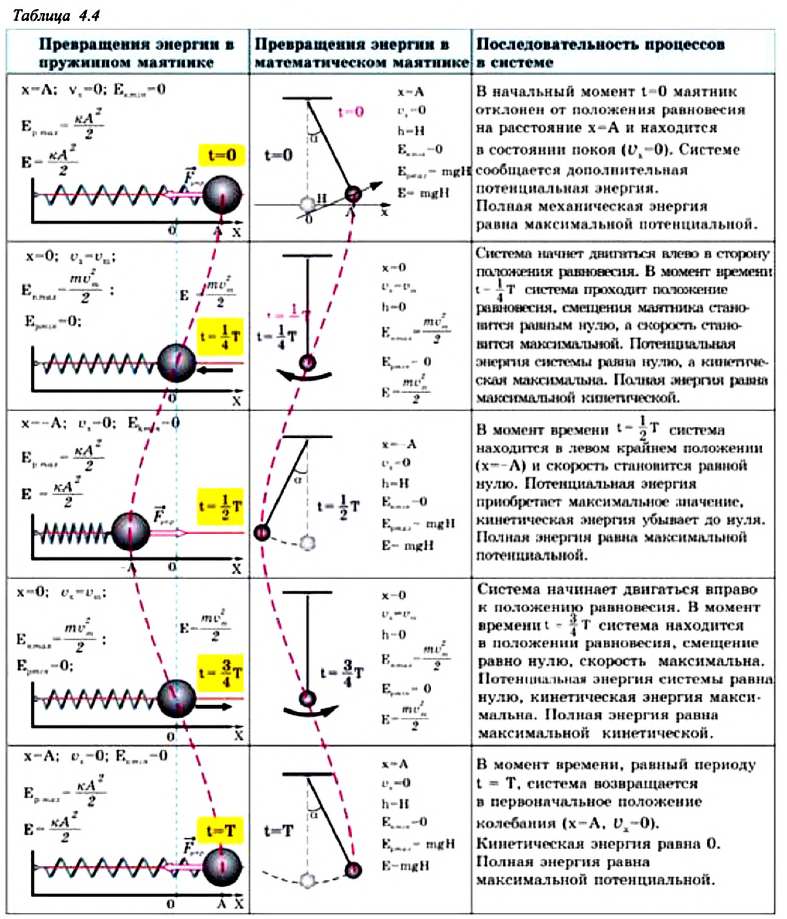
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 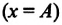имеет максимальное значение:

Если же маятник находится в точке равновесия, потенциальная энергия минимальна:

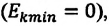
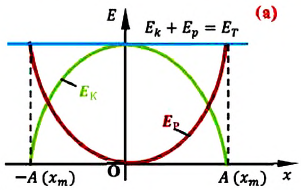
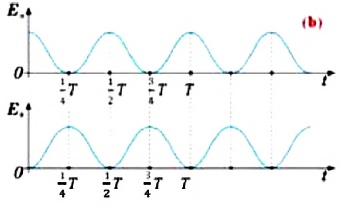
Кинетическая энергия системы, наоборот, в точке возвращения минимальна а в точке равновесия максимальна:

На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.

Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 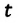остается постоянной (трение не учитывается):

a) для пружинного маятника:

b) для математического маятника:

Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):

Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:

• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.

Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:

Превращения энергии при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.

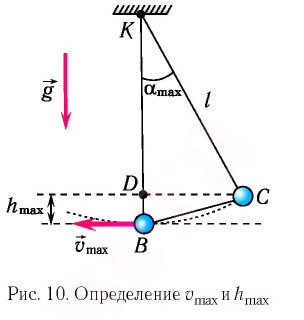
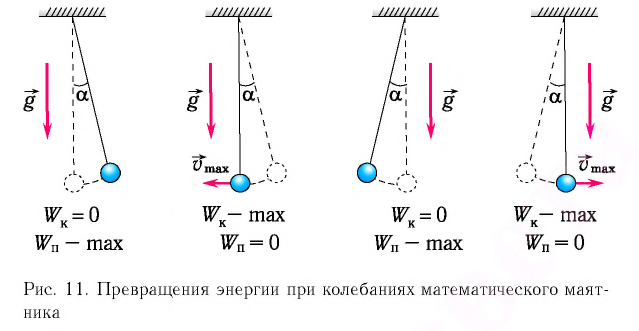
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

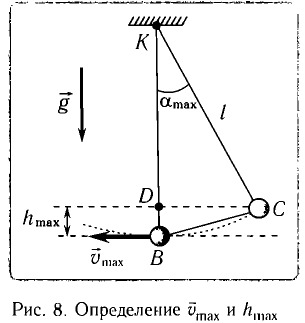
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

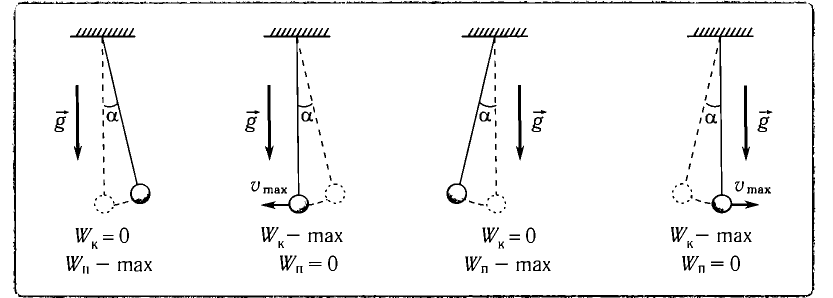
Рис. 7. Превращения энергии при колебаниях математического маятника

Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:

Из закона сохранения механической энергии следует (рис. 8), что

(1)

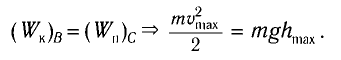
Отсюда найдем модуль максимальной скорости маятника:

(2)

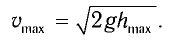
Высоту можно выразить через длину маятника l и амплитуду колебаний А.

Если колебания малые, то 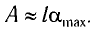Из треугольника KCD на рисунке 8 находим

Подставив выражение для в формулу I (2), получим

Подставляя выражения для 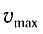и в соотношение (1), находим

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.

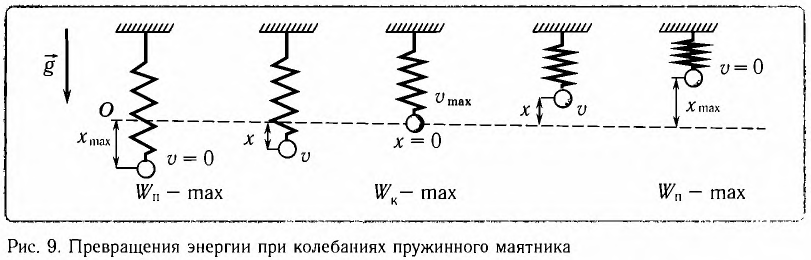
В любом промежуточном положении

Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 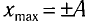, модуль его скорости равен нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:

где 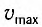— модуль максимальной скорости груза при колебаниях.

В промежуточных точках полная механическая энергия

Отсюда можно вывести выражение для модуля скорости 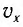груза в точке с

Так как

Энергия при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

При отклонении маятника на угол 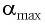(рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

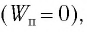
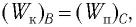
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю то из закона сохранения механической энергии следует (см. рис. 10), что т. е. кинетическая энергия маятника (а следовательно, и скорость) рис. ю. Определение^иhmax будет максимальна:

Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:

Отсюда найдем модуль максимальной скорости маятника:

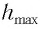
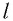
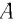
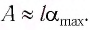
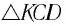
Высоту можно выразить через длину маятника и амплитуду колебаний. Если колебания малые, то Из (см. рис. 10) находим:

или

Подставив выражение (3) для 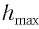в формулу (2), получим:

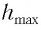
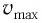
Подставляя выражения (3) для и (4) для в соотношение (1), находим:

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении

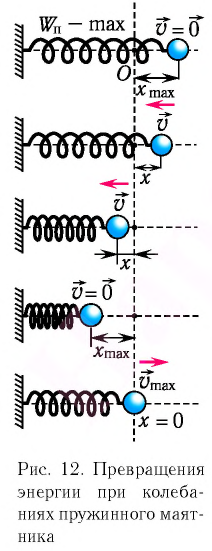
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).

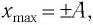
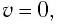
В крайних положениях, когда модуль скорости маятника и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда 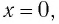вся энергия пружинного маятника переходит в кинетическую энергию груза:

где 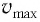— модуль максимальной скорости груза при колебаниях.

В положениях между крайними точками полная энергия

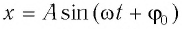
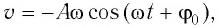
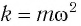
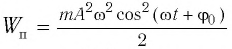
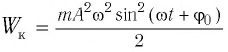
С учетом выражений для координаты и проекции скорости груза а также для находим его потенциальную энергию и кинетическую энергию в произвольный момент времени

Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:

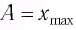
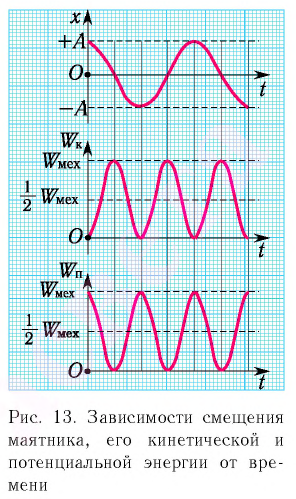
Таким образом, начальное смещение определяет начальную потенциальную, а начальная скорость определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.

Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).

Пример №1

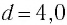
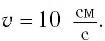
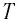
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние см и при прохождении положения равновесия достигает скорости, модуль которой Определите период колебании маятника.
Дано:

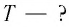
Решение

По закону сохранения механической энергии

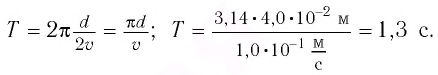
Ответ:

Пример №2

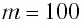
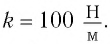
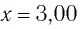
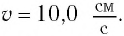
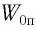
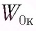
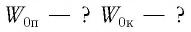
Груз массой г находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью Его смешают на расстояние см от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой Определите потенциальную и кинетическую энергию груза в начальный момент времени. Запишите кинематический закон движения груза.

Решение Потенциальная энергия груза: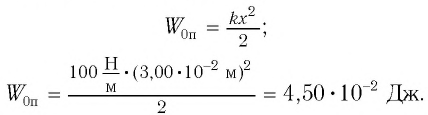

Кинетическая энергия груза:

Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:

Отсюда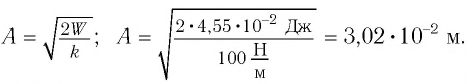

Циклическая частота: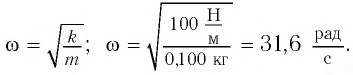

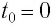
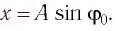
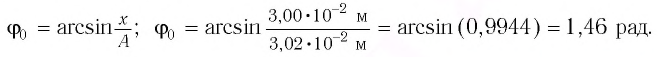
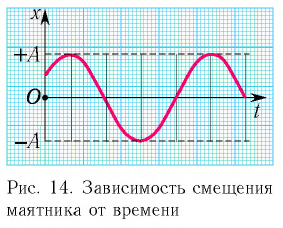
В начальный момент времени координата груза Отсюда начальная фаза:

Тогда закон гармонических колебаний имеет вид (рис. 14):

Ответ:

• Вынужденные колебания в физике
• Электромагнитные колебания
• Свободные и вынужденные колебания в физике
• Вынужденные электромагнитные колебания
• Закон Архимеда
• Движение жидкостей
• Уравнение Бернулли
• Механические колебания и волны в физике

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

🎬 Видео

11 класс. Скорость и ускорение при гармонических колебаниях. решение задач.Скачать

Урок 329. Задачи на гармонические колебания - 1Скачать

Физика 9 класс. §25 Гармонические колебанияСкачать

Уравнения механических колебанийСкачать

Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Колебательное движение. Уравнение гармонических колебаний | ФизикаСкачать

Кинематика. Практика 1 - Уравнения координаты и скоростиСкачать

Физика. Механика.Гармонические колебания.Скачать