Уравнение количества вещества через давление объем и температуру

Видео:Количество вещества. Моль. Число Авогадро. 8 класс.Скачать

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Видео:ТИПОВЫЕ ЗАДАЧИ ПО ХИМИИ: Химическое Количество Вещества, Моль, Молярная Масса и Молярный ОбъемСкачать

Конвертер величин

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Калькулятор закона состояния идеального газа (давление–объем–температура–количество)

Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.

Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.

Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.

Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.

Видео:Урок 141. Количество вещества. Молярная масса. Оценка размеров молекулСкачать

Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)

Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.

Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:

• Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
• Введите абсолютное давление P = 100 кПа.
• Введите объем V = 1 м³.
• Введите температуру T = 0 °C.
• Нажмите кнопку Рассчитать.
• Калькулятор покажет количество молей в 1 м 3 воздуха.
• Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
• Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль

Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

• Выберите T (Температура) в селекторе Выберите неизвестную величину.
• Введите молярную массу кислорода N = 32 г/моль.
• Введите массу кислорода m = 128 г.
• Калькулятор рассчитает количество кислорода в молях.
• Введите объем V = 4 л и давление P = 3 МПа.
• Нажмите кнопку Рассчитать.
• Считайте температуру в кельвинах.

Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).

Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:

• Выберите T (Температура) в селекторе Выберите неизвестную величину.
• Введите давление P = 500 кПа.
• Введите температуру T = 15 °C.
• Введите объем V = 5 л.
• Нажмите кнопку Рассчитать.
• Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
• Выберите Объем в селекторе Выберите неизвестную величину.
• Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
• Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.

Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.

Видео:Закон Авогадро. Молярный объем. 8 класс.Скачать

Определения и формулы

Идеальный газ

Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.

В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.

Закон идеального газа

Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:

• давление (P),
• объем (V),
• количество в молях (n),
• температура (T), and
• универсальная газовая постоянная (R)

Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:

Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:

• P — абсолютноедавление, измеряемое в СИ в паскалях (Па),
• V — объем, измеряемый в СИ в кубических метрах (м³),
• n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
• T — абсолютнаятемпература.
• R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.

Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.

Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро N_A и постоянной Больцмана k:

Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.

Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:

Заменяя в уравнении состояния идеального газа n на m/M, имеем:

Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль

Например, молярная масса кислорода как элемента в единицах системы СИ

Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:

Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:

Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:

Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать

Поскольку PV/NT — постоянная величина, можно записать это иначе:

Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.

Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.

Закон Бойля — Мариотта (T=const, n=const)

Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:

Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.

Закон Авогадро (T=const, P=const)

Если температура и давление остаются неизменными, можно записать

Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.

Закон Гей-Люссака (P=const, n=const)

При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.

В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).

Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)

Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:

Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Ограничения практической применимости:

• температуры ниже -100°C и выше температуры диссоциации / разложения
• давления выше 90 бар
• вакуум глубже чем 99%

Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.

• в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы
• в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире
• m-масса газа в (кг)
• M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)
• P-давление газа в (Па)
• Т-температура газа в ( °K)
• V-объем газа в м 3

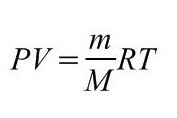Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.

1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.

Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.

Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V₁ и V₂, при температурах, соответственно, T₁ и T₂ и, пусть T₁ V₂ для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:

• показатели объемного счетчика газа тем «весомее», чем выше давление
• выгодно поставлять газ низкого давления
• выгодно покупать газ высокого давления

Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.

🎦 Видео

Связь между давлением, объёмом и температурой газаСкачать

Химия 8 класс (Урок№8 - Количество вещества. Молярная масса. Молярный объём газа. Закон Авогадро.)Скачать

Как Решать Задачи по Химии // Задачи с Уравнением Химической Реакции // Подготовка к ЕГЭ по ХимииСкачать

Количество теплоты, удельная теплоемкость вещества. 8 класс.Скачать

Как за 4 МИНУТЫ выучить Химию? Химическое Количество, Моль и Закон АвогадроСкачать

Решение задач на термохимические уравнения. 8 класс.Скачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Температура и тепловое равновесие. Определение температуры | Физика 10 класс #30 | ИнфоурокСкачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Урок 109 (осн). Задачи на вычисление количества теплотыСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Физика 10 класс : Объединенный газовый законСкачать