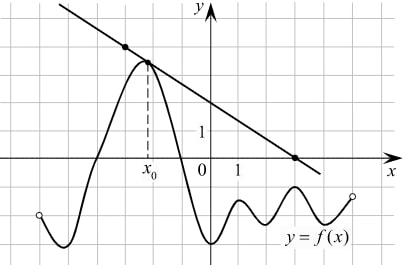
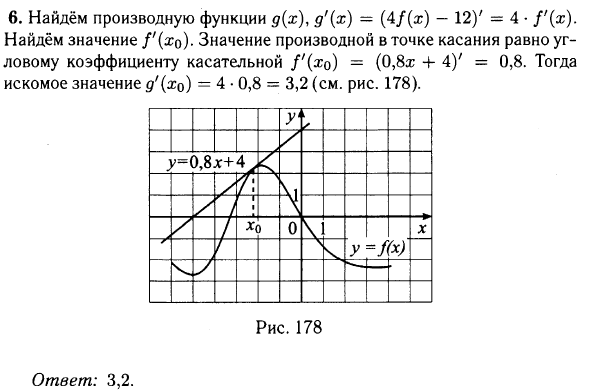
Уравнение касательной показано на рисунке найдите значение производной функции g x 12f x 6 13 (6 видео)

Решение №656 На рисунке изображены график функции f(x) и касательная к этому графику …

На рисунке изображены график функции y = f(x) и касательная к этому графику, проведённая в точке x₀. Найдите значение производной функции g(x) = 6f(x) − 3x в точке x₀.

Найдём производную функции g(x):

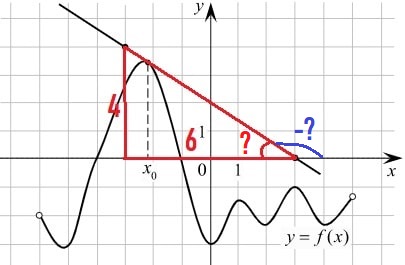
Найдём значение f′(x) в точке x₀. Оно равно тангенсу угла наклона касательной к оси Ох. Тангенс угла равен отношению противолежащего катета к прилежащему катету.

Мы нашли тангенс красного угла, тангенс же нужного нам синего угла, будет со знаком – .

tg α = f′(x) = – 2/3

Найдём значение g′(x):

g′(x) = 6 f′(x) – 3 = 6•( –2/3 ) – 3 = –4 – 3 = –7

Содержание

Задача 3146 На рисунке изображены график функции.
Условие
Решение
ЕГЭ для VIP
ЕГЭ по математике Профиль. Задание 6
ЕГЭ Профиль. Задание № 6
АЛГОРИТМ ВЫПОЛНЕНИЯ
1) Задачи на Физический смысл производной
2) Задачи на Геометрический смысл производной
3) Задачи на Применение производной к исследованию функций
4) Задачи на Первообразную
Тренировочные задания с самопроверкой
💥 Видео

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Задача 3146 На рисунке изображены график функции.

Условие

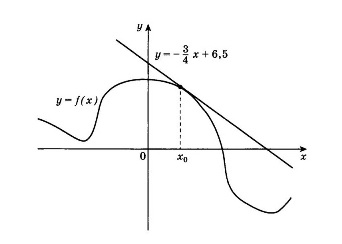
На рисунке изображены график функции y=f(x) и касательная к этому графику, проведённая в точке x0. Уравнение касательной показано на рисунке. найдите значение производной функции y=4*f(x)-3 в точке x0.

Решение

Нужно найти производную функции y= 4f(x)-3 в точке Х0.

То есть у′ = (4f(x)-3)′ = 4f′(х) — 0 = 4f′(x) в точке Х0.

Вспомним, что f′(х0) равно коэффициенту при х в уравнении касательной у = (-3/4)х + 6,5 к графику функции f(x) в точке х0.

Значит f(x0) = -3/4. Подставим это значение в у′:

у′ = 4f′(x0) = 4 * (-3/4) = -3 — это и есть искомое значение производной функции y= 4f(x)-3 в точке Х0.

Видео:ЕГЭ 2017 Профильный №7 найти производную в точке касания #7Скачать

ЕГЭ для VIP

Подготовке к ЕГЭ

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

ЕГЭ по математике Профиль. Задание 6

ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

ЕГЭ Профиль. Задание № 6

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 6 ЕГЭ профиль проверяет умение применять производную для решения прикладных задач. Такие задачи часто встречаются в физике и технических областях науки.

Задание состоит из текстовой задачи на определение физического, геометрического смысла производной, промежутков возрастания и убывания функции по её графику и графику её производной или первообразной. Ответом является целое число или конечная десятичная дробь.

При подготовке необходимо повторить правила нахождения производной, физический и геометрический смысл производной, понятие возрастания и убывания функции, понятие первообразной.

План выполнения задания № 6:

Внимательно прочитайте задачу.
Рассмотрите график. Определите, какой из графиков вам дан: функции, производной функции или первообразной функции. От ответа на данный вопрос зависит ход решения задачи.
Определите по графику необходимые значения.
Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

1) Задачи на Физический смысл производной

Задачи на применение физического смысла производной состоят из текста и выражения, описывающего уравнение движения материальной точки или тела.

Производная перемещения по времени выражает скорость движения: v(t) = x'(t) = at + v₀.
Производная скорости по времени выражает ускорение движения: a(t) = v'(t).

Задача № 6 (1). Материальная точка движется прямолинейно по закону x(t) = 2t 2 – 8t – 9, где х — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с начала движения. Найдите её скорость (в м/с) в момент времени t = 5с.
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 4t – 8.
При t = 5 имеем: v(5) = 4 • 5 – 8 = 12.
Ответ: 12.
Комментарий. Иногда в ответе получаются отрицательные числа, которые учащиеся рассматривают как ошибочный ответ.

Задача № 6 (2). Тело движется прямолинейно по закону: x(t) = 2t 3 + t – 1. В какой момент времени (в секундах) его ускорение будет равно 12 м/с 2 ?
Решение: Найдём закон изменения скорости: v(t) = x'(t) = 6t 2 + 1.
Ускорение — это производная скорости по времени: a(t) = v'(t) = 12t.
Чтобы найти, в какой момент времени ускорение было 12 м/с 2 , решим уравнение: 12t = 12. Отсюда t = 1 c.
Ответ: 1.
Комментарий. Обратите внимание: в задании нужно найти, в какой момент времени ускорение (не скорость!) будет равно 12 м/с 2 .

2) Задачи на Геометрический смысл производной

Задание ориентировано на умение выпускников читать и анализировать графики, содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

Геометрический смысл производной: угловой коэффициент касательной к графику функции в точке с абсциссой х₀ равен производной этой функции в точке х₀.
Геометрический смысл производной: k = tg a = f'(x)

Производная функции в точке с абсциссой х есть тангенс угла наклона касательной, проведённой к графику этой функции в точке (х₀; f(x₀)). При tg a > 0 производная функции положительна, при tg a f(x₀)).

Задача № 6 (3). На рисунке изображён график функции y = f(x) и отмечены пять точек на оси абсцисс: х₁, х₂, х₃, х₄, х₅. В скольких из этих точек производная функции f(x) отрицательна?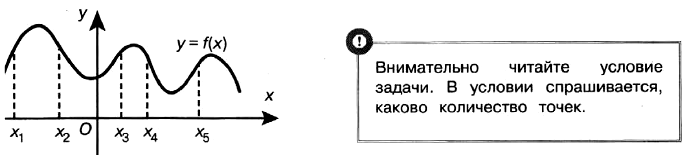

Решение: Производная функции отрицательна в тех точках, которые принадлежат участкам убывания функции. Это точки х₂, х₄ — всего 2 точки.
Ответ: 2.

Задача № 6 (4). На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. Пользуясь графиком, определите, в какой из данных точек значение производной наибольшее. В ответе укажите число, которое ей соответствует по таблице.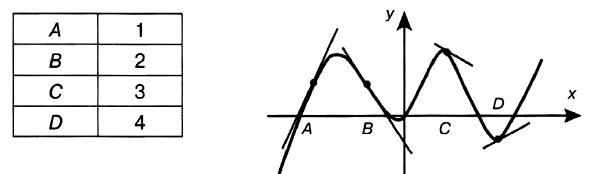

Решение: Производная функции положительна в точках А и D, так как в данных точках функция возрастает.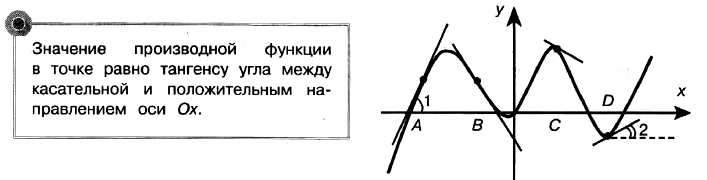

Угол 1 больше угла 2, значит, тангенс первого угла больше тангенса второго угла, соответственно, значение производной в точке А больше значения производной в точке D.
Ответ: 1.

Задача № 6 (5). На рисунке изображён график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику параллельна прямой у = 3х–2 или совпадает с ней.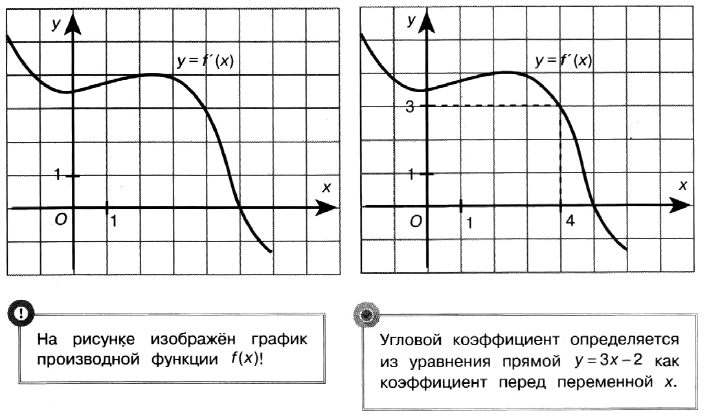

Решение: Поскольку касательная параллельна прямой у = 3х – 2 или совпадает с ней, она имеет угловой коэффициент, равный 3 (у’ = 3). Найдём, при каких х производная принимает значение 3. Из графика видно, что значению у = 3 соответствует точка х = 4.
Ответ: 4.

3) Задачи на Применение
производной к исследованию функций

Задание содержит задачи на определение или вычисление величин по графику, рассчитано на умение использовать знания в практической деятельности. При подготовке нужно повторить понятия: точка максимума, точка минимума, точки экстремума, убывание и возрастание функции, уравнение касательной к графику функции.

Если функция y = f(x) имеет экстремум в точке х₀, то в этой точке производная равна нулю или не существует.
Если f'(x) = 0 и при переходе через точку х₀ значения производной меняют знак с «+» на «–», то х₀ — точка максимума.
Если f'(x) = 0 и при переходе через точку х₀ значения производной меняют знак с «–» на «+», то х₀ — точка минимума.
Если f'(x) = 0 и при переходе через точку х₀ значения производной не меняют знак, то х₀ не является точкой экстремума.
Если в каждой точке х некоторого промежутка f'(х) > 0, то функция f(x) возрастает на этом промежутке.
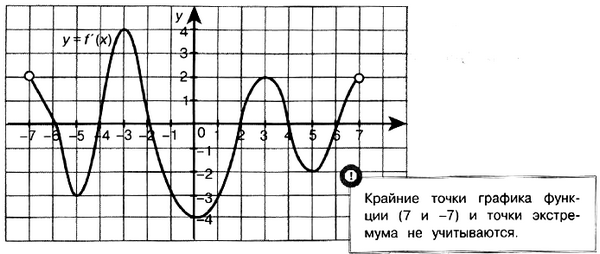
Если в каждой точке х некоторого промежутка f'(х) Задача № 6 (6). На рисунке изображён график производной функции f(x), определённой на интервале (–7; 7). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение: Промежутки возрастания данной функции f(x) соответствуют промежуткам, на которых её производная положительна, то есть промежуткам (–7; –6); (–4; –2); (2; 4); (6; 7). Данные промежутки содержат целые числа –3; 3. Их сумма равна 0.
Ответ: 0.
ПРИМЕЧАНИЕ: В ответе нужно указать сумму целых точек, входящих в промежутки возрастания.

4) Задачи на Первообразную

Функцию y = F(x) называют первообразной для функции y = f(x) на заданном промежутке х, если для всех х из этого промежутка верно равенство F'(x) = f(x).

Если функция y = F(x) является первообразной для функции y = f(x) на некотором промежутке, то и функция y = F(x) + C (С — постоянная) является первообразной для функции f на этом промежутке.

Пусть функция f(x) непрерывна на отрезке [а; b]. Тогда площадь трапеции, ограниченной линиями y = f(x); у = а; у = b и у = 0, равна F(b) – F(a), где F(x) — первообразная функции f(x).

Задача № 6 (7). На рисунке изображён график некоторой функции y = f(x). Пользуясь рисунком, вычислите F(5) – F(1), где F(x) — одна из первообразных функции f(x).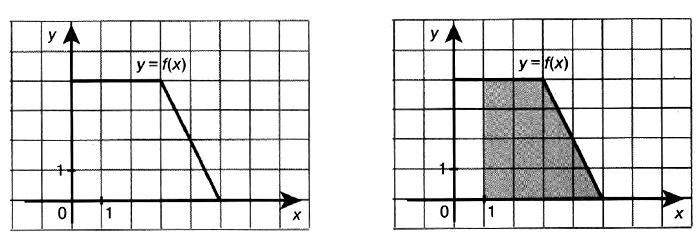

Решение: Разность значений первообразной в точках 5 и 1 равна площади выделенной на рисунке трапеции.
Площадь трапеции ограничена точками 1 и 5.
Площадь трапеции вычисляется по формуле S = h • (a + b)/2.
Из рисунка видно, что а =2, b = 4, h = 4. Значит, F(5) – F(1) = 4 • (2 + 4)/2 = 12.
Ответ: 12.
ПРИМЕЧАНИЕ: Если результат отрицательный или равен нулю, значит, в вычислениях была допущена ошибка.

Тренировочные задания с самопроверкой

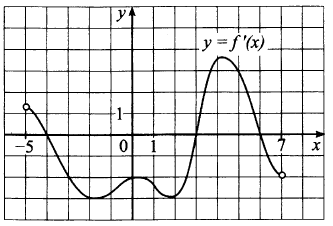
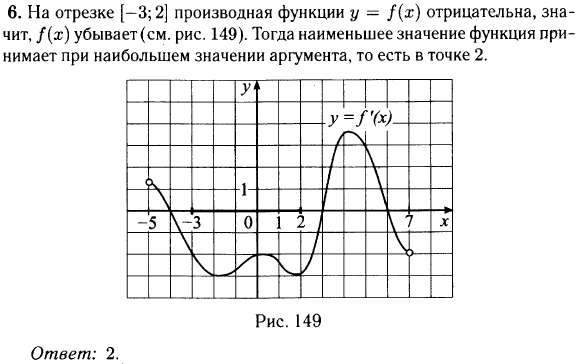
№ 6.1. На рисунке изображён график у = f’(x) – производной функции f(x), определённой на интервале (–5; 7). В какой точке отрезка [–3; 2] f(x) принимает наименьшее значение?

№ 6.2. Прямая у = 5х + 4 параллельна касательной к графику функции у = х 2 – 4х – 12. Найдите абсциссу точки касания.

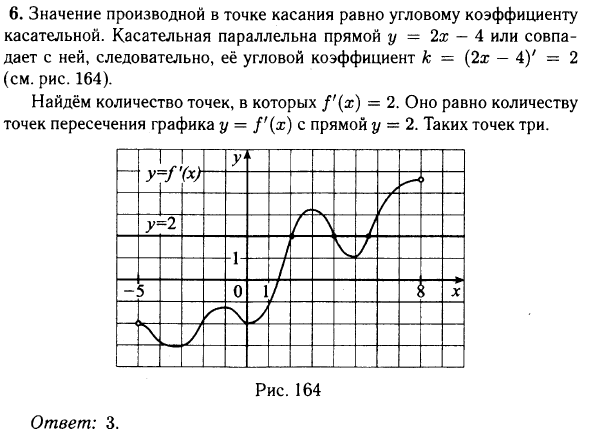
№ 6.3. На рисунке изображён график у = f‘(х) – производной функции f(х), определённой на интервале (–5; 8). Найдите количество точек, в которых касательная к графику функции f(х) параллельна прямой у = 2х – 4 или совпадает с ней.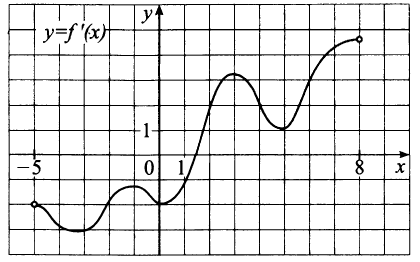

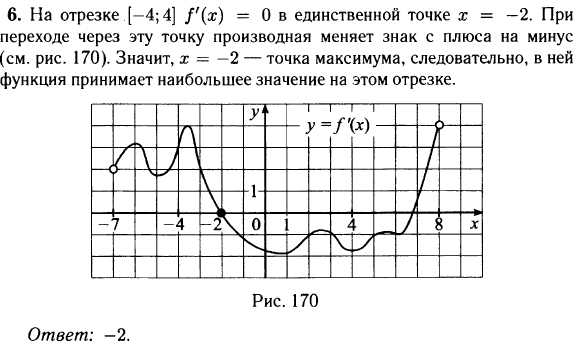
№ 6.4. На рисунке изображён график у = f‘(x) – производной функции f(x), определённой на интервале (–7; 8). Найдите, в какой точке отрезка [–4; 4] функция принимает наибольшее значение.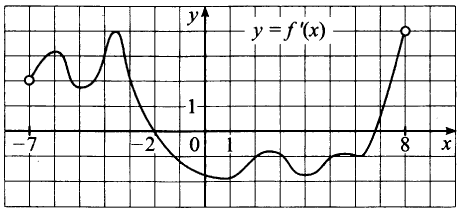

№ 6.5. На рисунке изображены график функции у = f(x) и касательная к этому графику, проведённая в точке x₀. Уравнение касательной показано на рисунке. Найдите значение производной функции g(х) = 4f(x) – 12 в точке x₀.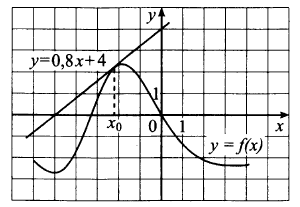

Вы смотрели: ЕГЭ по математике Профиль. Задание 6: Уметь выполнять действия с функциями. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.