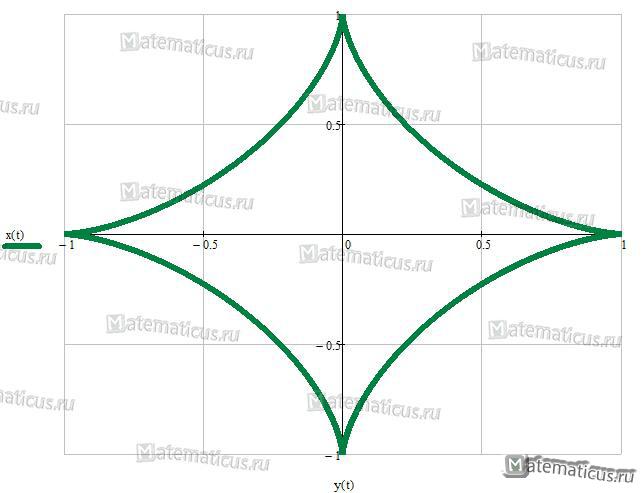
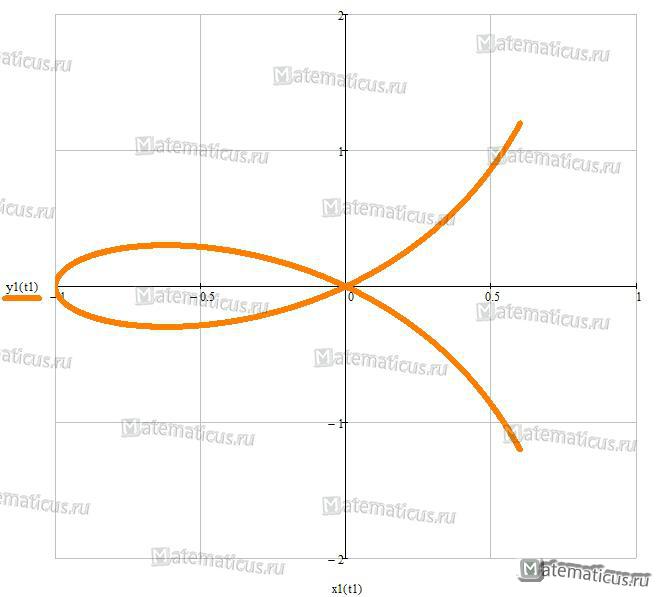
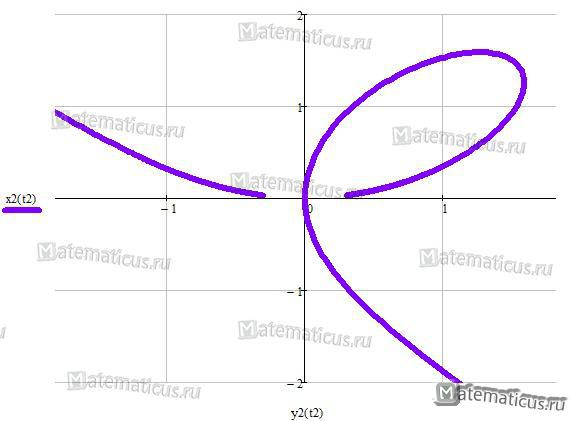
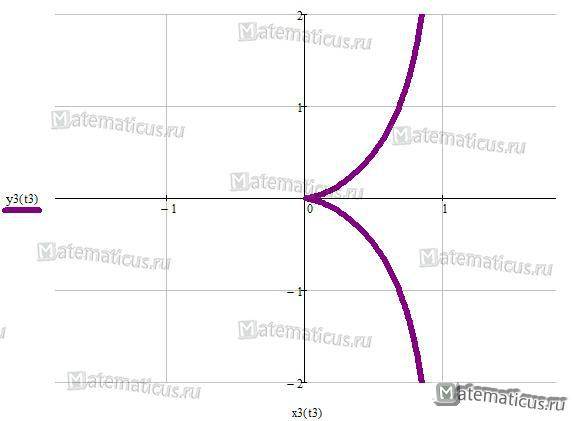
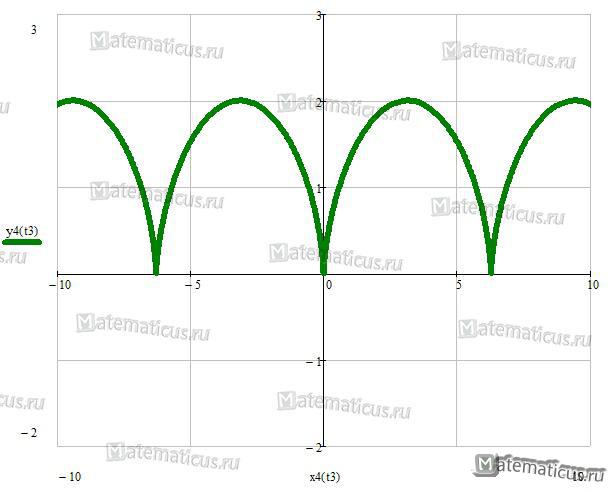
Уравнение кардиоиды в декартовых координатах (4 видео)

Уравнение кардиоиды в декартовых координатах

Кардиоида – плоская кривая, описываемая произвольной точкой М окружности радиуса r, катящейся без проскальзывания извне по другой, неподвижной, окружности того же радиуса – см. рис.

Кардиоида – частный случай эпициклоиды, одна из конхоид и улиток Паскаля.

Если над параболой выполнить преобразование инверсии с центром в фокусе параболы, то парабола перейдет в кардиоиду.

В прямоугольной декартовой системе координат кардиоиду можно задать уравнением
(x 2 + y 2 – 2rx) 2 = 4r 2 (x 2 + y 2 ),

где r – радиус окружности.
Как видно из уравнения, она является алгебраической кривой четвертого порядка и симметрична относительно оси абсцисс. Точка – точка возврата первого рода. Длина l дуги кардиоиды от точки K до точки М может быть вычислена по формуле
l = 16rsin 2 (φ/2),
a площадь, ограниченная кардиоидой, равна 6πr 2 .

Уравнение кардиоиды в полярных координатах (с полюсом на неподвижной окружности) имеет вид:
ρ = 2r(1 + cosφ).

Параметрические уравнения кардиоиды могут выглядеть так:
x = 2rcost – rcos2t; y = 2rsint – rsin2t.

Название кардиоиды происходит от греческих слов χαρδια – сердце, и ειδος – вид, вместе – сердцевидная.

Содержание

Замечательные кривые
Логарифмическая спираль
Кардиоида
Астроида
Строфоида
Декартов лист
Циссоида
Циклоида
Кохлеоида
Уравнения кривых. Кардиоида. Улитка Паскаля.
🎥 Видео

Видео:Видеоурок "Преобразование координат"Скачать

Замечательные кривые

Семейство роз Гранди

Уравнение имеет вид:

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

Рисунок 2 — роза с 16 лепестками ρ=sin8φ

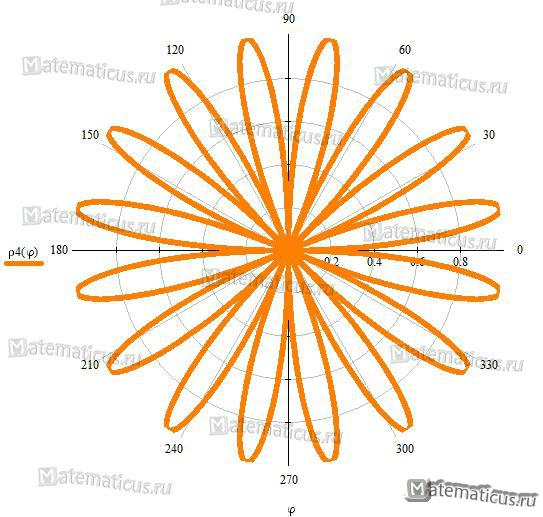
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

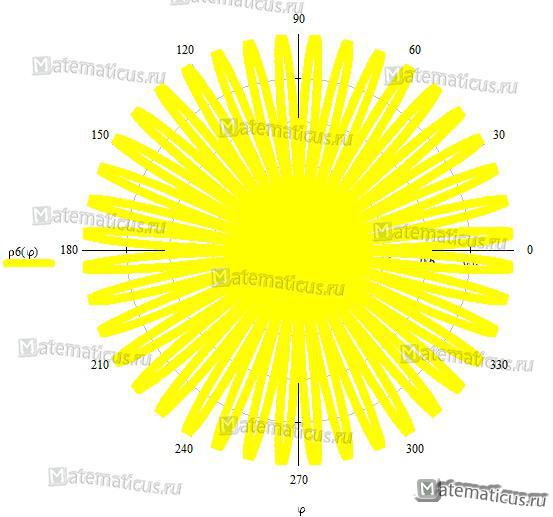
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

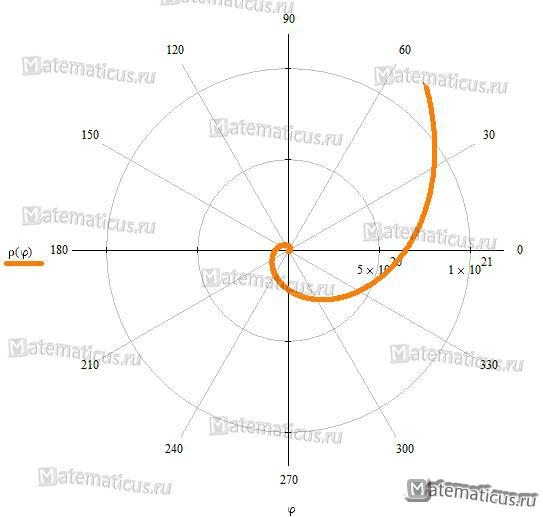
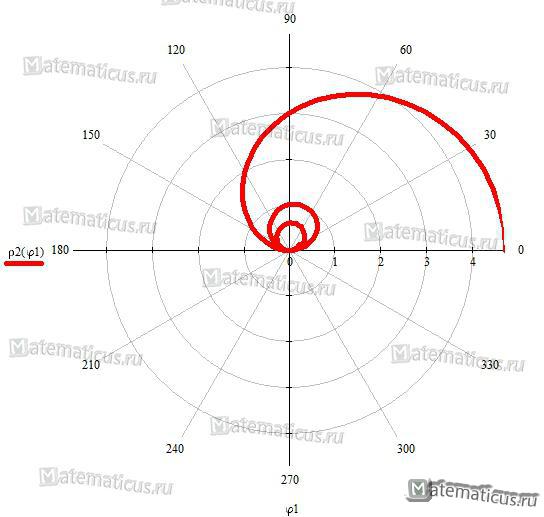
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

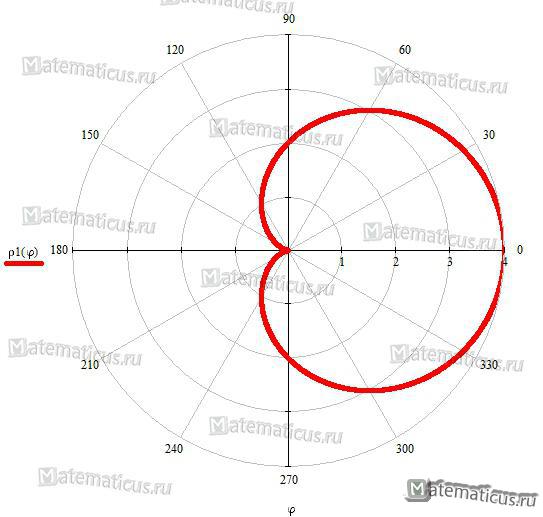
Кардиоида

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

Видео:Площадь кардиоиды.КардиоидаСкачать

Астроида

Уравнение астроиды (перев. греч. звезда и вид) :

x 2/3 + y 2/3 = a 2/3

Видео:Полярные в декартовыеСкачать

Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот) :

y 2 (a — x)= x 2 (a + x)

Уравнение строфоиды в полярной системе координат:

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Видео:Полярная система координатСкачать

Декартов лист

Уравнение декартова листа :

x 2 + y 2 — 3axy = 0

Уравнение декартова листа в полярной системе координат:

Видео:Полярная система координатСкачать

Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :

Параметрическое уравнение циссоиды:

x = a t 2 /(1 + t 2 )

x = a t 3 /(1 + t 2 )

Уравнение циссоиды в полярной системе координат:

Видео:Модель декартовой системы координат.Скачать

Циклоида

Параметрическое уравнение циклоиды :

Видео:Кардиоида и нефроида, в общем - эпициклоида. Вывод параметрического уравнения.Скачать

Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

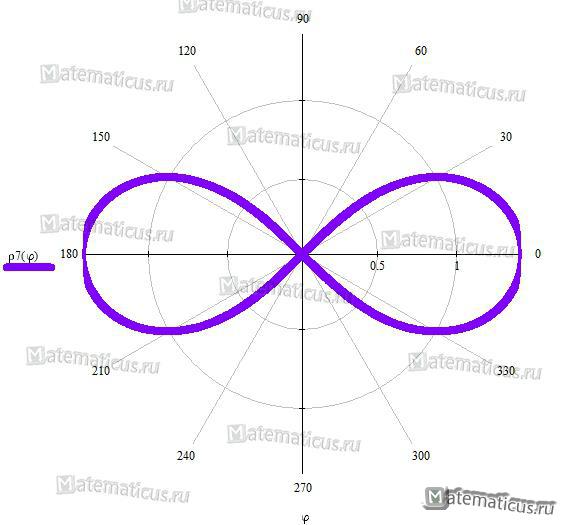
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Уравнение лемниската Бернулли в полярных координатах:

Архимедова спираль рассмотрена здесь подробно.

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

Видео:Построение кривой в полярной системе координатСкачать

Уравнения кривых. Кардиоида. Улитка Паскаля.

Если применить две окружности с равными радиусами и вращать одну вокруг другой, то образуется кардиоида(греч. кардиа — сердце) — математики считают, что сформированная кривая отдаленно схожа с сердцем.

Если брать точку не на самой катящейся окружности, а внутри ее, сместив в сторону от центра, тогда будет образована кривая, получившая название Улитка Паскаля или лимакона.

Пусть a – диаметр исходной окружности, а l — расстояние, на которое смещается точка вдоль радиус – вектора. Тогда возможны такие варианты улитки Паскаля: а > l, a = l и a 2 + у 2 +2аx) 2 – 4a 2 (х 2 + у 2 ) = 0;